что делать с парадоксом

Что такое парадокс — просто о сложном (с примерами)

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Данное понятие родилось в Древней Греции и означает мнение, противоречащее здравому смыслу.

В широком смысле слово парадокс – это явление, ситуация, событие, кажущиеся невероятными и не соответствующие привычным представлениям людей о реальности в силу необычного контекста.

Парадокс — это когда невозможное возможно

Суть парадоксального суждения заключается в том, что начав его рассматривать и исследовать, вы постепенно найдете в нем логику, здравое зерно и придете к умозаключению, что невозможное возможно.

Для лучшего понимания какого-либо термина необходимо обратиться к его антониму (что это такое?). Таковым для парадокса является слово ортодокс – что значит традиционность, постоянство, проверенность. В этом же смысле парадокс описывается как неожиданный, оригинальный, непривычный.

Чтобы предвосхитить путаницу, также следует научиться отличать парадокс от апории. Если первое – это нелогичная правда, то второе – логичная выдумка.

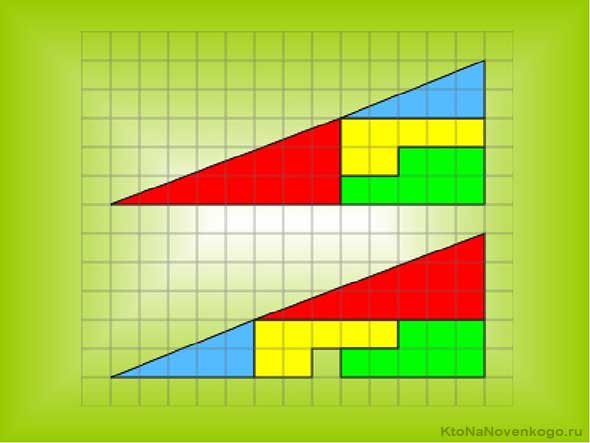
P.S. Если вы не знаете ответ на приведенную выше геометрическую загадку, то не спешите относить ее к теме сегодняшней статьи. Таки нет, это всего лишь апория (ловкий трюк, вводящий в заблуждение). Подробности смотрите ниже (пункт 5 в примерах).

Правда, в некоторых случаях такие расхождения – это всего лишь ошибки, допущенные в ходе экспериментального опыта. Поэтому в научной среде парадокс представляет собой полезное явление, так как мотивирует ученых искать дополнительные методы для изучения теории, минимизировать искажение реальности.

Примеры парадоксов

Чтобы еще лучше понять и усвоить значение этого понятия приведу классические, известные во всем мире примеры.

Далее Ахиллесу нужно преодолеть этот метр, но черепаха уже продвинулась дальше. Каждый раз, когда человек будет достигать крайнюю точку, в которой находилось животное, последнее будет находиться уже в следующей. А так как существует бесконечное число точек, то следуя этой логике, догнать черепаху не представляется возможным.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (8)

Медицина у нас бесплатная, а без денег не лечат. Образование в стране бесплатное, но каждый месяц нужно платить. А что говорят власти по этому поводу: это парадокс, такого не может быть!)

Я заметила, что люди особенно любят находить парадоксы в том, что касается качества жизни. К примеру, не работает, а деньги всегда есть.

Для меня парадокс — это некая загадка, которой трудно найти логическое объяснение.

Наша жизнь полна парадоксов, а явление это прекрасно тем, что хоть где-то сохраняется интрига))

Юлия, а нет парадокса в том, что люди работают много и получают при этом мало! Они ведь сами настраивают себя на то, что такое положение вещей неизбежно и оно будет всегда. Только сами этого не осознают.

Нет никакого парадокса и в том, что большие деньги зарабатываются легко, так как зарабатывающий их настраивает себя на получение высокой прибыли и верит в то, что по-другому не бывает.

Раньше любил такого рода загадки, но со временем понял, что они только отнимают время и ничего не дают.

1. Курица или яйцо? Процесс установления – генетическая мутация, следовательно первой явилась курица, так как мутация в эмбриональной клетке вероятнее, чем в клетках всей курицы. Курица могла появиться из яйца, но не совсем куриного.

2. Гегель утверждал, что начало любого явления есть установление процесса. Парадокс лжеца. Процесс вранья содержит две компоненты: изречение и его оценку. Оценка оценки, как требует «парадокс», не снимает надобность в первой компоненте. Это не парадокс, а неполнота описания.

3. Парадокс неожиданной казни. Нарушение логики, а не парадокс. Исключение пятницы предполагает прожитые понедельник — среду и четверг. Не прожил четверг – бойся.

4. Всемогущества нет. У меня было пять яблок. Яблоки я отдал, оставив себе «пять». Теперь я математик.

6. «Парадокс» о черепахе и Ахиллесе. Нагло ограничиваете время рассмотрения задачи. Зачем устанавливать предел перемещения и делать невинными глазки?

10. Куча – это форма, а не количество.

11. Движение – это изменение положения в промежуток времени. Не в момент, а между двумя моментами.

Действительно парадокс – наведенный идиотизм на светлые детские головы.

Источник

masterok

Мастерок.жж.рф

Хочу все знать

Парадоксы — интересная штука и существуют они со времен древних греков. Однако, говорят, что при при помощи логики можно быстро найти фатальный недостаток в парадоксе, который и показывает, почему, казалось бы невозможное, возможно или что весь парадокс просто построен на недостатках мышления.

Опровергнуть парадокс конечно не потяну, мне бы хотя бы понять полностью суть каждого. Это не всегда просто. Вот проверьте…

12. Парадокс Ольберса

В астрофизике и физической космологии парадокс Ольберса – это аргумент, говорящий о том, что темнота ночного неба конфликтует с предположением о бесконечной и вечной статической Вселенной. Это одно из свидетельств нестатической Вселенной, такое как текущая модель Большого взрыва. Об этом аргументе часто говорят как о “темном парадоксе ночного неба”, который гласит, что под любым углом зрения с земли линия видимости закончится, достигнув звезды. Чтобы понять это, мы сравним парадокс с нахождением человека в лесу среди белых деревьев. Если с любой точки зрения линия видимости заканчивается на верхушках деревьев, человек разве продолжает видеть только белый цвет? Это противоречит темноте ночного неба и заставляет многих людей задаться вопросом, почему мы не видим только свет от звезд в ночном небе.

11. Парадокс всемогущества

Парадокс состоит в том, что если существо может выполнять какие-либо действия, то оно может ограничить свою способность выполнять их, следовательно, оно не может выполнять все действия, но, с другой стороны, если оно не может ограничивать свои действия, то это что-то, что оно не может сделать. Это, судя по всему, подразумевает, что способность всемогущего существа ограничивать себя обязательно означает, что оно действительно ограничивает себя. Этот парадокс часто формулируется в терминологии авраамических религий, хотя это и не является обязательным требованием. Одна из версий парадокса всемогущества заключается в так называемом парадоксе о камне: может ли всемогущее существо создать настолько тяжелый камень, что даже оно будет не в состоянии поднять его? Если это так, то существо перестает быть всемогущим, а если нет, то существо не было всемогущим с самого начала. Ответ на парадокс заключается в следующем: наличие слабости, такой как невозможность поднять тяжелый камень, не попадает под категорию всемогущества, хотя определение всемогущества подразумевает отсутствие слабостей.

10. Парадокс Сорита

Парадокс состоит в следующем: рассмотрим кучу песка, из которого постепенно удаляются песчинки. Можно построить рассуждение, используя утверждения: — 1000000 песчинок – это куча песка — куча песка минус одна песчинка – это по-прежнему куча песка. Если без остановки продолжать второе действие, то, в конечном счете, это приведет к тому, что куча будет состоять из одной песчинки. На первый взгляд, есть несколько способов избежать этого заключения. Можно возразить первой предпосылке, сказав, что миллион песчинок – это не куча. Но вместо 1000000 может быть сколь угодно другое большое число, а второе утверждение будет верным при любом числе с любым количеством нулей. Таким образом, ответ должен прямо отрицать существование таких вещей, как куча. Кроме того, кто-то может возразить второй предпосылке, заявив, что она верна не для всех “коллекций зерна” и что удаление одного зерна или песчинки все еще оставляет кучу кучей. Или же может заявить о том, что куча песка может состоять из одной песчинки.

9. Парадокс интересных чисел

Утверждение: не такого понятия, как неинтересное натуральное число. Доказательство от противного: предположим, что у вас есть непустое множество натуральных чисел, которые неинтересны. Благодаря свойствам натуральных чисел, в перечне неинтересных чисел обязательно будет наименьшее число. Будучи наименьшим числом множества его можно было бы определить как интересное в этом наборе неинтересных чисел. Но так как изначально все числа множества были определены как неинтересные, то мы пришли к противоречию, так как наименьшее число не может быть одновременно и интересным, и неинтересным. Поэтому множества неинтересных чисел должны быть пустыми, доказывая, что не существует такого понятия, как неинтересные числа.

8. Парадокс летящей стрелы

Данный парадокс говорит о том, что для того, чтобы произошло движение, объект должен изменить позицию, которую он занимает. В пример приводится движение стрелы. В любой момент времени летящая стрела остается неподвижной, потому как она покоится, а так как она покоится в любой момент времени, значит, она неподвижна всегда. То есть данный парадокс, выдвинутый Зеноном еще в 6 веке, говорит об отсутствии движения как таковом, основываясь на том, что двигающееся тело должно дойти до половины, прежде чем завершить движение. Но так как оно в каждый момент времени неподвижно, оно не может дойти до половины. Этот парадокс также известен как парадокс Флетчера. Стоит отметить, что если предыдущие парадоксы говорили о пространстве, то следующий парадокс – о делении времени не на сегменты, а на точки.

7. Парадокс Ахиллеса и черепахи

В данном парадоксе Ахиллес бежит за черепахой, предварительно дав ей фору в 30 метров. Если предположить, что каждый из бегунов начал бежать с определенной постоянной скоростью (один очень быстро, второй очень медленно), то через некоторое время Ахиллес, пробежав 30 метров, достигнет той точки, от которой двинулась черепаха. За это время черепаха “пробежит” гораздо меньше, скажем, 1 метр. Затем Ахиллесу потребуется еще какое-то время, чтобы преодолеть это расстояние, за которое черепаха продвинется еще дальше. Достигнув третьей точки, в которой побывала черепаха, Ахиллес продвинется дальше, но все равно не нагонит ее. Таким образом, всякий раз, когда Ахиллес будет достигать черепаху, она все равно будет впереди. Таким образом, поскольку существует бесконечное количество точек, которых Ахиллес должен достигнуть, и в которых черепаха уже побывала, он никогда не сможет догнать черепаху. Конечно, логика говорит нам о том, что Ахиллес может догнать черепаху, потому это и является парадоксом. Проблема этого парадокса заключается в том, что в физической реальности невозможно бесконечно пересекать поперечно точки – как вы можете попасть из одной точки бесконечности в другую, не пересекая при этом бесконечность точек? Вы не можете, то есть, это невозможно. Но в математике это не так. Этот парадокс показывает нам, как математика может что-то доказать, но в действительности это не работает. Таким образом, проблема данного парадокса в том, что происходит применение математических правил для нематематических ситуаций, что и делает его неработающим.

6. Парадокс Буриданова осла

Это образное описание человеческой нерешительности. Это относится к парадоксальной ситуации, когда осел, находясь между двумя абсолютно одинаковыми по размеру и качеству стогами сена, будет голодать до смерти, поскольку так и не сможет принять рациональное решение и начать есть. Парадокс назван в честь французского философа 14 века Жана Буридана (Jean Buridan), однако, он не был автором парадокса. Он был известен еще со времен Аристотеля, который в одном из своих трудов рассказывает о человеке, который был голоден и хотел пить, но так как оба чувства были одинаково сильны, а человек находился между едой и питьем, он так и не смог сделать выбора. Буридан, в свою очередь, никогда не говорил о данной проблеме, но затрагивал вопросы о моральном детерминизме, который подразумевал, что человек, столкнувшись с проблемой выбора, безусловно, должен выбирать в сторону большего добра, но Буридан допустил возможность замедления выбора с целью оценки всех возможных преимуществ. Позднее другие авторы отнеслись с сатирой к этой точке зрения, говоря об осле, который столкнувшись с двумя одинаковыми стогами сена, будет голодать, принимая решение.

5. Парадокс неожиданной казни

4. Парадокс парикмахера

Предположим, что существует город с одним мужским парикмахером, и что каждый мужчина в городе бреется налысо: некоторые самостоятельно, некоторые с помощью парикмахера. Кажется разумным предположить, что процесс подчиняется следующему правилу: парикмахер бреет всех мужчин и только тех, кто не бреется сам. Согласно этому сценарию, мы можем задать следующий вопрос: парикмахер бреет себя сам? Однако, спрашивая это, мы понимаем, что ответить на него правильно невозможно: — если парикмахер не бреется сам, он должен соблюдать правила и брить себя сам; — если он бреет себя сам, то по тем же правилам он не должен брить себя сам.

3. Парадокс Эпименида

2. Парадокс Эватла

Это очень старая задача в логике, вытекающая из Древней Греции. Говорят, что знаменитый софист Протагор взял к себе на учение Эватла, при этом, он четко понимал, что ученик сможет заплатить учителю только после того, как он выиграет свое первое дело в суде. Некоторые эксперты утверждают, что Протагор потребовал деньги за обучение сразу же после того, как Эватл закончил свою учебу, другие говорят, что Протагор подождал некоторое время, пока не стало очевидно, что ученик не прикладывает никаких усилий для того, чтобы найти клиентов, третьи же уверены в том, что Эватл очень старался, но клиентов так и не нашел. В любом случае, Протагор решил подать в суд на Эватла, чтобы тот вернул долг. Протагор утверждал, что если он выиграет дело, то ему будут выплачены его деньги. Если бы дело выиграл Эватл, то Протагор по-прежнему должен был получить свои деньги в соответствии с первоначальным договором, потому что это было бы первое выигрышное дело Эватла. Эватл, однако, стоял на том, что если он выиграет, то по решению суда ему не придется платить Протагору. Если, с другой стороны, Протагор выиграет, то Эватл проигрывает свое первое дело, поэтому и не должен ничего платить. Так кто же из мужчин прав?

1. Парадокс непреодолимой силы

Парадокс непреодолимой силы представляет собой классический парадокс, сформулированный как “что происходит, когда непреодолимая сила встречает неподвижный объект?” Парадокс следует воспринимать как логическое упражнение, а не как постулирование возможной реальности. Согласно современным научным пониманиям, никакая сила не является полностью неотразимой, и не существует и быть не может полностью недвижимых объектов, так как даже незначительная сила будет вызывать небольшое ускорение объекта любой массы. Неподвижный предмет должен иметь бесконечную инерцию, а, следовательно, и бесконечную массу. Такой объект будет сжиматься под действием собственной силы тяжести. Непреодолимой силе потребуется бесконечная энергия, которая не существует в конечной Вселенной.

Источник

Парадокс

– Что такое парадокс?

– Как парадокс помогает сделать шутку смешнее?

– Как пошутить про себя?

Стив Каплан в своей книге «Скрытые инструменты комедии» пишет:

«Однажды я проводил семинар в компании Disney и спросил: «Над чем вы сейчас работаете?». И они сказали: «Заканчиваем одну штуку, называется «Суперсемейка» (The Incredibles). «О чем это?», – спросил я. «Ну, – ответили они, – это история о целой семье супергероев, которые вынуждены отказаться от своих способностей, потому что это ставит их вне закона, и теперь им надо найти нормальную работу».

И я сказал: «Бог мой, это же великолепно! Значит, там есть сцена, где они супергерои, а есть – где они работают в офисе? И потом наверняка есть сцена семейной ссоры, только с применением суперсилы?». И так я «предсказал» примерно треть или половину сцен из фильма, не потому, что я такой умный, а потому, что сама идея так пришлась мне по вкусу».[1]

Я же предлагаю шагнуть чуть дальше и оттолкнуться от понятия «удачная предпосылка», которую Каплан рассматривает как божественное озарение, и приземлиться на землю, чтобы спокойно разобрать, как создавать удачные предпосылки.

Итак, вторым типом шуток является парадокс. А нам понадобится различать типы и приемы. Разница в том, что любая шутка относится к какому-либо типу. Однако сами по себе типы шуток нам не помогают решать задачу создания шуток. А вот приемы – это инструменты для создания шуток.

Что же такое парадокс? В исходном понимании, я думаю, каждый сталкивался с этим словом. Слово очень знакомое, оно означает совмещение несовместимого.

То есть, допустим, я вам скажу: «Что, ребята, сейчас приготовьтесь, внимательно смотрите на экран, потому что я вам сейчас покажу миниатюру «Гитлер в детском саду»».

Наш мозг работает, таким образом, что нам тут же становится интересно. То есть, в большинстве случаев я уверен, что вам будет интересно, вы заинтересовались, чем продолжится эта миниатюра. Фокус в том, что на самом деле никакой миниатюры нет. Но почему интересна миниатюра «Гитлер в детском саду»? Потому что в этом словосочетании сопоставлены две несопоставимые вещи.

То есть, допустим, «тощий обжора» или «Николай Валуев в «Танцах со звездами»». Нам сразу же становится интересно, кто победит. Нам интересно, потому что совмещены две сущности, которые заряжены очень разнополярно. То есть, если мы представим парадокс в виде двух полей: в виде облака и земли, то интерес возникает тогда, когда между облаком и землей возникает молния, то есть создается гроза. Когда это происходит?

Когда облако очень сильно положительно заряжено, а земля очень отрицательно заряжена. Соответственно, когда облако трётся о землю, возникает молния. Соответственно, нужны очень разнополярно заряженные символы.

Вернёмся. Предпосылка «Гитлер в фашистской Германии» никакого интереса у зрителя не вызывает, потому что мы это все уже видели. Если вы возьмете «Николай Валуев на ринге», то это тоже мы уже видели. Если вы скажете: «Сергей Лазарев на сцене фестиваля «Новая волна»», вы все это уже видели, мозг не заинтересовывается, он практически на это не реагирует, пропускает мимо своего внимания. Потому что мозг человека ленив, он устроен таким образом, что хочет видеть только что-то новое, что-то, чего он раньше не видел. А тратить энергию на концентрацию внимания на предсказуемых историях он не желает. И спасибо ему за это.

Кстати, в этом как раз и секрет того, почему нам не нравятся шутки, повторенные дважды, почему мы не смеемся. Потому что молния возникает только один раз.

Соответственно, простой прием, который вы можете изучить сразу, это – возьмите персонажа, который заряжен каким-то определенным образом, допустим, Сергея Лазарева.

У нас есть понимание, что он такой сладенький и мягкий человек. Поместите его в пространство, которое обладает антонимичными свойствами. Раз он сладенький, то есть, нужно что-то горькое и противное. Если он мягкий, то нужно что-то жесткое, горькое, противное. Например, «Сергей Лазарев в фашистской Германии» или «Сергей Лазарев в переходе на Левобережной», «Сергей Лазарев на Чемпионате мира по кроссфиту».[2]

Таким образом, можете бесконечно создавать названия для миниатюр. По сути, огромное количество КВНовских миниатюр, миниатюр в «Камеди клабе», и тому подобных шоу, построено на этом принципе – вы совмещаете несовместимое. Я имел счастье долгое время наблюдать за тем, как работает дуэт «Мазурин и Антошкин». Парни сначала придумывали название миниатюры, а потом уже сочиняли содержание. Допустим, «Лев Лещенко в очереди на почте». Нам тут же интересно.

Почему возникает этот интерес? Потому что нам интересно, что победит: Лев Лещенко, и вся очередь на почте будет себя вести, как он, высоко, чинно, статно, или наоборот, Льву Лещенко придётся спуститься до уровня почты России. И так в каждом из случаев. То есть, нам интересно «Николай Валуев в танцах со звездами» – это ситуация, когда он будет танцевать что-то вроде бокса, и его партнерше придётся боксировать с ним и укрываться от его ударов, то есть победит сила символа Николай Валуев. Или, наоборот, в «Танцах со звездами» он будет отплясывать ча-ча-ча и чечетку. Нам интересно, что будет происходить.

Точно также и с Гитлером. По сути, наш мозг заинтересовывается потому, что есть два варианта развития, он хочет узнать, что произойдет. «Гитлер в детском саду» – это будет детский сад, в котором все будет по-гитлеровски, где дети будут ходить строем, они будут отбирать игрушки у других детей, и все будут плакать. Это будет очень грустный такой, жестокий детский сад. Либо это будет наоборот: Гитлер будет маленьким, добрым таким, веселым, и у него отберут игрушку, и так мы узнаем, почему он стал злым.

Заявляя парадокс, вы сразу предлагаете два варианта событий, а когда вы предлагаете две альтернативы, мозг сразу заинтересовывается. Вот в этом весь секрет.

Давайте посмотрим дальше, как же нам с этим работать, что же мы можем с этим полезного сделать.

С парадоксами все гораздо проще нежели с каламбурами, потому что парадоксы построены на полярности.

2. Взяли его свойство

4. Взяли пространство с антонимичными свойствами

К каждому предмету у вас должна быть какая-то ассоциация, то есть, если вы видите плюшевую игрушку, то тут же понимаете – это детство: «Ага, плюшевая игрушка».

Где может плюшевая игрушка оказаться, чтобы нам стало интересно, чтобы это пространство было парадоксальным для плюшевой игрушки. Допустим, «плюшевая игрушка в пивном баре на столе сидит». Нам тут же интересно, почему она здесь сидит: здесь был ребенок, или это какой-то мужчина, впавший в детство. Почему здесь плюшевая игрушка? То есть сразу же совмещены несовместимые пространства, несовместимые символы, нас это заинтересовывает.

Вы можете поупражняться сами, давайте я вам сейчас нарочно дам персону. Поместите в какое-нибудь пространство Дональда Трампа. В каком пространстве он был бы парадоксален?

Поместите в какое-нибудь пространство Кристину Агилеру, поместите в какое-нибудь пространство Терминатора 2, жидкого терминатора, где нам было бы интересно посмотреть на развитие событий.

И вторая часть упражнения: возьмите несколько пространств и подумайте, каких персонажей вы туда бы поместили. [3]

Допустим очень дорогой ресторан, например «Прага».

Например, ночной клуб, кого бы мы хотели увидеть в ночном клубе?

Калифорния Голливуд. Кого бы мы хотели увидеть в Голливуде?

Вы увидите, что парадоксальность возникает прямо на лету, вы сможете прямо сейчас это проверить.

Что мне еще нравится в парадоксах?

Они выводят создание смешного практически на технический уровень, потому что вы получаете какой-то символьный запрос, обрабатываете, каким типичным свойством обладает объект, и тут же помещаете его в парадоксальное пространство, воспользовавшись антонимом.

Что здесь важно понимать: если у вас не получается создать какой-то парадокс, или вы не видите какой-то парадоксальной вещи, то тут важно вычленить главное качество, свойство. Докопаться до самой сути. Получить одно слово.

В какой-то момент мозг сам начнет вам подсказывать верные ходы, но даже если сейчас вы испытываете с этим затруднение, то пройдите по этому длинному пути из упражнений и книг, и он вас точно приведет к интересным зарисовкам. Вы не пожалеете.

Важно понимать еще одну вещь: чем более поляризован ваш парадокс, то есть, чем больше заряд ваших частиц, тем лучше. Если вы возьмете просто слова «хулиган» и «отличник», то это слабо заряженные частицы, потому что мозг приблизительно понимает, что эти люди постоянно пересекаются, и они находятся в одной плоскости. Чаще всего в каждом классе есть и хулиган, и отличник, соответственно, эти плюс и минус не сильно между собой растянуты, а значит, молния не будет очень мощной, и это важно понимать.

Но при этом, если мы растянем, мы возьмем отличника и поляризуем, то есть, возьмем самого, самого, самого на свете отличника, допустим, Анатолия Вассермана или, допустим, Дмитрия Медведева, который тоже выглядит по поведению отличником. И теперь возьмем хулигана, самого хулиганистого хулигана, то есть Анатолий Вассерман и какой-нибудь боец MMA, весь в наколках, какой-нибудь колумбиец, который выглядит очень агрессивным и хулиганистым. А теперь представим: Анатолий Вассерман и Федор Емельяненко застряли в лифте…

На самом деле, шутки никакой нет, но уже интересно, что будет дальше. О чем они будут говорить? Как поведут себя? Кто победит?

Огромная работа уже проведена по затачиванию своего мозга на систематизацию этого знания. Но сами шутки вы можете сочинять самостоятельно также быстро.

В парадоксах важно ещё то, что они, на самом деле, касаются не только комедии, или, как сказал бы один из величайших ораторов и мыслителей нашего времени: «Не только лишь комедии». Парадоксы касаются и драмы точно также. И даже фильмов ужасов.

Попробуйте оценить фильмы ужасов, которые сейчас выходят, в этих фильмах леденящим душу объектом чаще всего становится то, что раньше не пугало, потому что фильм ужасов, где злодеем является чудовище из леса или инопланетянин, никому уже не интересен. А вот, когда главным злодеем в фильме ужасов оказывается мама, как в фильме «Мама», – вот это круто. Или клоун, или беременная женщина, или ее плод, или ребенок, как в фильме «Омен».

Или возьмём драму в любом фильме, допустим, в «Калифорникейшен», в чём строится драма? Да, он суперлюбовник, и все женщины его хотят, но драма в том, что он любит одну единственную. Вот парадокс: его хотят все, а он любит одну. И вот на этом строится сезон за сезоном, это нам интересно.

«Гравитация» – у нее нет причин жить, но она единственная, кто спаслась после катастрофы.

«Король говорит» – он король, и он единственный, кто может вдохновит нацию на сопротивление фашизму, но… он заика.

Если это работает в драме, то что уж говорить о комедиях. Уверен, некоторые комедии создавались не из сценария, а из названия.

«Дедсадовский полицейский». «Блондинка в законе». «Нищий из Беверли-Хиллз».

Рассмотрим примеры: полицейский – это суровый дядька, привыкший решать проблемы силой. Где его суперсила не работает? В детском саду, потому что там никто не подчиняется законам.

Блондинка идеальна при подборе одежды и выборе аксессуаров. Где это все не работает? В юридическом институте.

Беверли-Хиллз – дорогой район, где живут богачи. Кого мы меньше всего ожидаем увидеть там? Нищего.

Более того, этот принцип работает и при выборе актеров.

Сарик Андреасян, режиссер фильма «Беременный»: «Успех фильма в том, что мы позвали на роль беременного мужчины Дюжева, актёра с брутальным прошлым. Если бы ошиблись с актёром, завалили бы проект».

Далее вы увидите, что это знание позволит вам усмешнять любой материал. Порой, все, чего не хватает шутке новичка, это растянутости полюсов. Теперь вы знаете, что делать.

Источник