что такое абсолютная шкала
АБСОЛЮТНАЯ ШКАЛА
Смотреть что такое «АБСОЛЮТНАЯ ШКАЛА» в других словарях:
абсолютная шкала — Шкала отношений (пропорциональная или аддитивная) безразмерной величины. Примечания 1. Отличительные признаки абсолютных шкал: наличие естественных (не зависящих от принятой системы) единиц нуля и безразмерной единицы измерений, допустимость… … Справочник технического переводчика
абсолютная шкала — 2.2.5 абсолютная шкала : Шкала отношений (пропорциональная или аддитивная) безразмерной величины. Источник: РМГ 83 2007: Государственная система обеспечения единства измерений. Шкалы измерений. Термины и определения … Словарь-справочник терминов нормативно-технической документации
АБСОЛЮТНАЯ ШКАЛА — См. шкала, абсолютная … Толковый словарь по психологии
Абсолютная шкала температур — Хаотическое тепловое движение на плоскости частиц газа таких как атомы и молекулы Существует два определения температуры. Одно с молекулярно кинетической точки зрения, другое с термодинамической. Температура (от лат. temperatura надлежащее… … Википедия
абсолютная шкала температур — absoliučioji temperatūros skalė statusas T sritis Standartizacija ir metrologija apibrėžtis Nesisteminis termodinaminės temperatūros skalės pavadinimas. atitikmenys: angl. absolute temperature scale vok. absolute Temperaturskala, f rus.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
абсолютная шкала потенциалов — absoliučioji potencialų skalė statusas T sritis Standartizacija ir metrologija apibrėžtis Elementų potencialai, išdėstyti pagal Hg nulinio krūvio potencialą. atitikmenys: angl. absolute potential scale rus. абсолютная шкала потенциалов, f pranc.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
абсолютная шкала потенциалов — absoliučioji potencialų skalė statusas T sritis chemija apibrėžtis Elementų potencialai, išdėstyti pagal Hg nulinio krūvio potencialą. atitikmenys: angl. absolute potential scale rus. абсолютная шкала потенциалов … Chemijos terminų aiškinamasis žodynas
абсолютная шкала температур — absoliučioji temperatūros skalė statusas T sritis fizika atitikmenys: angl. absolute temperature scale vok. absolute Temperaturskala, f rus. абсолютная шкала температур, f pranc. échelle absolue des températures, f … Fizikos terminų žodynas
абсолютная шкала температур — шкала Кельвина … Cловарь химических синонимов I
Логарифмическая абсолютная шкала — Логарифмическая шкала измерений, получаемая логарифмическим преобразованием абсолютных шкал, когда в выражении L = log X под знаком логарифма X безразмерная величина, описываемая абсолютной шкалой. Примечание. Другое название этой разновидности… … Словарь-справочник терминов нормативно-технической документации
Измерение. Шкалы измерений
Известное изречение гласит «все познается в сравнении».
Для идентификации объектов и их характеристик во множестве их проявлений требуется большое количество и разнообразие мер. С учетом особенностей измеряемых объектов и задач измерений меры группируют и используют для построения шкал измерений.
Шкала измерений – упорядоченное множество проявлений количественных или качественных характеристик объектов, а также самих объектов. Указанное множество может быть образовано из наименований и обозначений (в том числе в цифровой форме) объектов и их характеристик, а также из значений и числовых значений (для количественных характеристик).
Согласно РМГ 83-2007 [7] «шкала измерений – отображение множества различных проявлений количественного или качественного свойства на принятое по соглашению упорядоченное множество чисел или другую систему логически связанных знаков (обозначений)». «Измерение – сравнение конкретного проявления измеряемого свойства (величины) со шкалой измерений этого свойства (величины) в целях получения результата измерений (оценки свойства или значения величины)».
Под качественной характеристикой в определении шкалы измерений и далее понимается описание объектов, их свойств и состояний, в словесной форме, в том числе с использованием наименований и обозначений.
Количественная характеристика – характеристика, которая может быть представлена числовым значением, равным отношению количественного содержания этой характеристики к еѐ базовой реализации, называемой единицей измерения.
Шкала наименований – шкала, состоящая из множества наименований (обозначений) объектов или проявлений их характеристик, в соответствии которым поставлено описание объекта (конкретная реализация объекта, его графическое изображение, математическая формула, график и т.п.) или проявлений его характеристик.
Наименование (обозначение) в этом случае рассматривают как обобщенную характеристику объекта или его свойств и состояний. С помощью шкалы наименований устанавливают эквивалентность (равноценность) измеряемого объекта или его характеристик и описания, поставленному в соответствие тому или иному наименованию (обозначению). Это позволяет отнести объект к какой-либо группе или выделить его, путем присвоения индивидуального наименования (обозначения), после чего наименования (обозначения) применяются как идентификаторы объектов (характеристик объектов). При построении шкал наименований могут использоваться числа, но лишь как метки объектов. Примерами таких шкал являются: атласы цветов (до 1000 наименований), запахов (сырой, затхлый, кислый и т.д.), вкуса (чистый, полный, гармоничный и т.д.); множество номеров телефонов, автомашин, паспортов; разделение людей по полу, расе, национальности; классификаторы промышленной продукции, специальностей высшего образования; терминологические справочники и т.п.
Числа, знаки, обозначения, наименования, составляющие шкалу наименований, разрешается менять местами. Для результатов измерений, полученных с использованием этой шкалы, нет отношений типа «больше — меньше», не применимы понятия единица измерения, нуль, размерность. С ними могут проводиться только некоторые математические операции. Например, числа нельзя складывать и вычитать, но можно подсчитывать, сколько раз (как часто) встречается то или иное число.
Оценки экспертов часто осуществляются с использованием шкал порядка. Типичным примером являются задачи ранжирования и классификации промышленных объектов, подлежащих экологическому страхованию.
В отличие от шкалы наименований шкала порядка позволяет не только установить факт равенства или неравенства измеряемых объектов, но и определить характер неравенства в виде суждений: «больше — меньше», «лучше — хуже» и т.п. Однако нельзя утверждать, что землетрясение в 2 балла (лампа качнулась под потолком) ровно в 5 раз слабее, чем землетрясение в 10 баллов (полное разрушение всего на поверхности земли).
Шкалы наименований и порядка, для которых не определены единицы измерений, называют также условными шкалами или не метрическими шкалами.
Абсолютная шкала – шкала числовых значений количественной характеристики. Отличительные признаки абсолютных шкал: наличие естественного нуля и отсутствие необходимости в единице измерений. С использованием абсолютных шкал измеряют коэффициенты усиления, ослабления, амплитудной модуляции, нелинейных искажений, отражения, коэффициент полезного действия и т. п. Результаты измерений в абсолютных шкалах при необходимости выражают в процентах, промилле, байтах, битах, децибелах.
Разновидностью абсолютных шкал являются дискретные (счетные) шкалы, в которых результат измерения выражается числом частиц, квантов, или других объектов, эквивалентных по проявлению измеряемого свойства. Например, шкалы для электрического заряда ядер атомов, числа квантов (в фотохимии), количества информации. Иногда за единицу измерений (со специальным названием) в таких шкалах принимают какое-то определенное число частиц (квантов), например один моль – число частиц, равное числу Авогадро.
Абсолютная шкала, диапазон значений которой находится в пределах от нуля до единицы (или некоторого предельного значения по спецификации шкалы) называют абсолютной ограниченной шкалой.
Шкалы разностей (интервалов), отношений и абсолютные классифицируют как метрические или физические шкалы. Эти шкалы допускают логарифмическое преобразование, часто применяемое на практике, что приводит к изменению типа шкал. Такие шкалы называют логарифмическими. Практическое распространение получили логарифмические шкалы на основе применения систем десятичных и натуральных логарифмов, а также логарифмов с основанием два.
Практически реализация шкал измерений достигается путем стандартизации как самих шкал и единиц измерений, так и, при необходимости, способов и условий (спецификаций) их однозначного воспроизведения.
Измерение с помощью шкал заключается в установлении соответствия объекта или его характеристики отметке на шкале измерений. После чего объекту измерений приписывают количественную или качественную определенность, соответствующую выявленной отметке шкалы.
Шкала измерений
Высокое качество продукции любого предприятия напрямую зависит от точности и общего качества измерений. Мы не можем решить, соответствует ли конкретный образец продукции требованиям заказчика, если не выразим эти требования количественно или качественно. Для сравнения какого-либо параметра с его заданным значением служат шкалы измерений.
Виды шкал измерений
Суть измерения состоит в том, что текущему состоянию объекта ставится в соответствие некоторое число, порядковый номер или символ.
Что такое шкала
Совокупность таких чисел, номеров или символов и называется шкалой измерений
По своему типу выделяют следующие виды шкал:
Шкалы также относят к одной из двух групп:
Шкалы также делятся по их силе. Чем больше сведений об объекте измерений можно извлечь из результатов измерений по ней. Самыми сильными считаются абсолютные шкалы, самыми слабыми — номинальные. Иногда исследователи усиливают шкалу, характерным примером является «оцифровка» номинальных шкал. Качественным признакам присваивают некое их числовое выражение. Это облегчает обработку результатов, особенно компьютерную. Важно помнить, что оцифровка не придает качественным признакам всех свойств, которыми обладают числа. К такой шкале можно применять операции сравнения, но нельзя — сложения, вычитания и т.п.
Шкалы измерения по Стивенсу
Шкалы измерений
Рассмотрим шкалы измерений подробнее.
Номинальная
Самые простые измерительные шкалы – номинальные. Они относятся к качественным и отражают те или иные свойства объекта, выраженные словесно. Их элементы могут только совпадать или не совпадать друг другом, Их нельзя сопоставлять по принципу «больше-меньше». Недопустимы также и арифметические действия.
Характерным примером может служить группа крови. Первая группа не больше третьей и не может быть сложена с четвертой. У человека может быть только одна группа крови, и измерение
Порядковая
По ней можно ранжировать и сравнивать объекты, по какому — либо признаку, например, расположить людей в строю по росту. Иванов больше Сидорова, а Сидоров больше Кузнецова.
Из этих данных можно сделать вывод о том, что Иванов выше Кузнецова, но нельзя определить, насколько именно.
Интервалов
Она состоит из заранее определенных и равных между собой интервалов. И является намного более информативной. Свойство объекта соотносится с одним из таких интервалов.
Характерным примером такой шкалы измерений может служить принятое у людей исчисление времени. Период оборота Земли вокруг Солнца делится на 365 дней, дни делятся на часы, далее на минуты и секунды. Мы можем соотнести событие с одним из таких интервалов: «эта статья была написана в 2018 году» или «Дождь начнется в 14 часов»
Значения в этом случае можно сравнивать друг с другом не только качественно, но и количественно, становятся доступны операции сложения и вычитания. «Заход солнца произойдет на 12 часов позже восхода». «Фильм А длиннее фильма В на 25 минут»
Однако поскольку начало отсчета не установлено, невозможно определить, во сколько раз одно значение больше другого.
Отношений
Точкой начала отсчета является точка, в которой значение параметра равно нулю. Появляется возможность отсчитывать от нее абсолютное значение параметра, определять разницы значений и во сколько раз одно больше другого. Характерный пример — температурная шкала Кельвина. За начало отчета взята точка «абсолютного нуля», при которой прекращается тепловое движение материи. Второй опорной точкой выбрана температура таяния льда при нормальном давлении. Разница между этими точками по Цельсию составляет 273 °C, и один градус Кельвина равен одному градусу Цельсия. Таким образом, можно сказать, что лед тает при 273К.
Отношений – наиболее информативная. На ней возможны все арифметические операции-
Деление, умножение сложение и вычитание значений параметра будет иметь физический смысл. Мы можем вычислить не только насколько одно значение больше другого, но и во сколько раз.
Разностей
Представляет собой частный случай интервальных. Для них значение не меняется при произвольном числе сдвигов на определенный параметр. Другими характерными признаками являются
В качестве примера можно привести циферблат часов – каждые сутки значение времени будет, например, «7 часов», хотя это разные дни.
Другим примером может служить компас, показывающий направление из одной точки. Сама эта точка может иметь различные координаты.
Важно помнить, что в этом случае при измерении мы можем вычислять разницу между двумя значениями, но должны все время помнить о том, что начальное значении задано произвольно. Например, при переходе на летнее время придется задать новое начальное значение.
Абсолютная
Абсолютная шкала занимает высшую ступень в шкальной иерархии. Единицы их естественные и не основаны на соглашениях и допущениях. Кроме того, эти единицы не имеют размерности, не служат производными системы СИ или какой-либо другой. Они всегда безразмерны:
Абсолютные подразделяют на
Иерархия шкал измерений
Условная иерархия составляется по признаку силы.
По мере возрастания силы увеличивается конкретность информации об объекте.
Шаг влево, шаг вправо — шкала. Или от абсолюта к простому порядку
Так уж получилось в нашей Вселенной, что все (или почти все) сигналы природного происхождения – аналоговые. Для большинства задач их обработки, анализа, распознавания и т.п. необходимо, в первую очередь, преобразовать сигнал в цифровые данные (ведь у нас как никак век цифровых технологий, ага). Для этого используют аналого-цифровое преобразование. Тема настолько хорошо всем известная, что не о чем, вроде-бы, и говорить (за исключением конкретной техники преобразования, но статья не об этом). Однако давайте, все-таки, углубимся в эту тему и рассмотрим ее под необычным углом зрения.
Для применения классических процедур обработки сигналов требуется выполнение операций сложения и умножения, следовательно, требуется представление отсчетов в абсолютной шкале. А могут ли для обработки сигналов применяться другие шкалы, в каких случаях и что это дает? Об этом рассказывается в данной статье.
Заранее авторы извиняются за приличный объем, но это служит для максимально ясного освещения вопроса. И немного о применении шкального кодирования для оценки энтропии мы уже говорили вот тут
1. Понятие о шкалах
Классическое аналого-цифровое преобразование каждому отсчету входного сигнала ставит в соответствие номер интервала на шкале амплитуд, в который этот отсчет попадает (рис. 1).
Рис. 1. Принцип аналого-цифрового преобразования
Данную процедуру в отношении каждого отсчета можно рассматривать как единичное измерение. Ширина интервала АЦП определяет максимальную погрешность такого измерения. В теории измерений (см., например, [1]), вводится понятие измерительных шкал (шкал сравнения). Упомянем некоторые из них.
2. Шальные Шкальные представления числовых временных рядов
Относительные шкалы находят естественное применение при оцифровке данных качественного характера. Например, когда измеряемые характеристики принимают значения из множества <плохой, хороший, очень хороший>. Но если исходные данные представляют собой числа, то какой смысл представлять их в относительной шкале? И как с ними потом работать? Рассмотрим ответы на эти два вопроса.
Сначала определимся с мотивацией для представления числовых данных в относительных шкалах. В обычном аналого-цифровом преобразовании, принцип которого представлен на рис. 1, соотношение уровней входного сигнала и значений выходных данных фиксировано и не зависит от времени. Отсюда следуют, что любые два отсчета в выборке сравнимы между собой, то есть мы можем определить, какой из них больше и насколько. Всегда ли эти утверждения оправданы с точки зрения природы входных данных? Допустим, мы оцениваем скорость ветра по углу отклонения вершин деревьев (например, обрабатывая записи с камер видеонаблюдения). Можно ли утверждать, что вдвое больший угол отклонения соответствует вдвое большей скорости ветра? Очевидно, нет, связь здесь нелинейная и ее параметры нам точно неизвестны.
Однако мы можем по углам наклона деревьев сравнить скорости ветра в два произвольных момента времени и определить, какая из них больше. Таким образом, абсолютная шкала здесь избыточна, ее использование не только приводит к неэффективному кодированию, но и создает почву для необоснованных суждений (что в науке чревато). В то же время, для представления этих данных достаточно порядковой (ранговой) шкалы, которая порождает код меньшей длины, чем абсолютная, и кодирует только достоверную информацию.
Рассмотрим следующий пример. Зададимся вопросом: «Насколько простой карандаш сегодня стоит больше, чем в 1970 году?». Формально ответить на вопрос несложно, так как цены известны. Но этот ответ не будет иметь никакого смысла, так как 1 рубль 1970 года и 1 рубль 2016 года – несравнимы (в смысле реального наполнения). Следовательно, мы вообще не можем определить, больше или меньше он стоит сегодня по сравнению с 1970 годом. Однако и в 1970 году и в 2016 мы можем сравнить его стоимость со стоимостями других товаров, либо сравнить его стоимости по месяцам тех же лет. Таким образом, для некоторых числовых рядов значения сравнимы только в пределах определённого временного интервала. Для таких рядов ранговое кодирование не подходит, так как оно предполагает сравнимость всех отсчетов временного ряда. В этом случае следует применять другой тип порядковой шкалы, описанный ниже (локально-ранговое кодирование).
Прежде чем перейти к рассмотрению непосредственно процедур рангового и локально-рангового кодирования, несколько слов о практическом значении всех этих рассуждений. Как уже понятно из сказанного, использование абсолютной шкалы там, где она не соответствует природе данных, приводит к двум негативным последствиям:
Насколько распространены подобные данные? В экономике – почти все, связанные с ценами и различными курсами. В социологии и статистике, например, данные о заболеваемости населения за разные периоды. Их нельзя сравнивать, так как изменялось качество медицинской диагностики. В анализе статистических рядов – когда мы имеем дело с индексами, отражающими интересующий нас показатель, но, возможно, нелинейным образом. В электронике и радиотехнике подобные ситуации возникают там, где имеют место некомпенсируемые нелинейные преобразования и неконтролируемые (паразитные и пр.) модуляции сигнала. Пример – измерение потенциала в электроэнцефалографии, результат, как правило, промодулирован переменным подэлектродным сопротивлением, так что сравнивать можно только близлежащие во времени отсчеты.
Насколько значимы выявленные нами проблемы? Ведь стоимость хранения данных с развитием технологий падает, а от некорректных суждений можно просто воздержаться. Дело в том, что сегодня человечество порождает значительно больше данных, чем может обработать, и этот разрыв растет. Для его преодоления создаются т.н. системы и технологии больших данных (Big Data). Применение шкального кодирования данных в соответствии с их природой может существенно повысить эффективность технологий их автоматической обработки. Во-первых, на этой основе значительно снизится скорость входного потока. Во-вторых, процедуры машинного обучения, автоматического выявления закономерностей и т.п. будут работать более корректно, опираясь только на значимые свойства исходных данных. Вообще, процедура подготовки данных для автоматизированного анализа имеет огромное значение, и шкальное кодирование здесь может сыграть свою роль.
Теперь рассмотрим конкретные методы шкального кодирования данных.
3. Ранговое кодирование числовых рядов
Ранговое кодирование известно давно и применяется, в частности, в статистике для непараметрической проверки гипотез. Для сигнала, приведенного на рис. 1, соответствующий ранговый код приведен на рис. 2. Он получается заменой отсчета его рангом, то есть порядковым номером в отсортированной по возрастанию выборке.
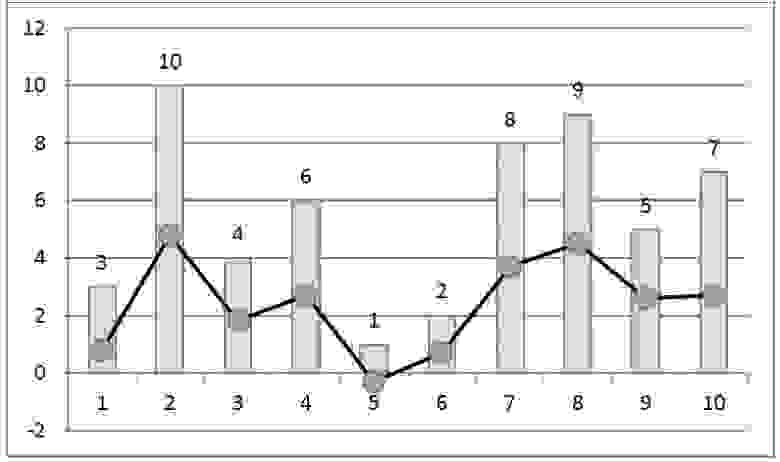
Рис. 2. Ранговое кодирование временного ряда. Линия с маркерами – исходный сигнал, столбики – ранги отсчетов.
Недостатком такого кодирования является его нелокальность в том смысле, что добавление новых элементов к выборке изменяет ранги всех отсчетов. В частности, ранг максимального по значению отсчета всегда равен количеству отсчетов в выборке. Помпе с соавторами [2] предложили делить значения рангов на число элементов в выборке. В результате полученный код всегда находится в интервале [0,1] и влияние новых отсчетов на ранги остальных значительно снижается (рис. 3).
Рис. 3. Ранговое кодирование временного ряда по алгоритму Помпе с соавт. [2]. Линия с маркерами – исходный сигнал, столбики – ранги отсчетов.
4. Локально-ранговое кодирование числовых рядов
Проблема нелокальности рангового кода решается и другим методом – с использованием локально-рангового кодирования. Для этого мы должны задать интервал сравнимости, в пределах которого соотношения отсчетов выборки считаются значимыми и должны быть сохранены. Соотношения отсчетов, отстоящих друг от друга более, чем на интервал сравнимости, при кодировании не учитываются.
В процессе локально-рангового кодирования подбирается такой код, элементы которого повторяют соотношения между отсчетами исходного ряда, отстоящими друг от друга не более, чем на интервал сравнимости. Для примера на рис. 3 приведен такой код с интервалом сравнимости в 2 отсчета. Это означает, что для каждого отсчета сохранены соотношения с ближайшими двумя отсчетами слева и справа.
Рис. 4. Локально-ранговое кодирование временного ряда. Линия с маркерами – исходный сигнал, столбики – локальные ранги отсчетов.
5. Символьное представление временных рядов
Ранги отсчетов (глобальные, нормированные, локальные) представлены числами. На самом деле числами они не являются, так как операции сложения и вычитания рангов смысла не имеют. Ранги отражают только знак разности между двумя отсчетами, но не ее величину. Таким образом, ранги представляют собой множество, элементы которого упорядочены отношением ≤. Такое множество всегда можно отобразить на некоторый алфавит, так как символы алфавита упорядочены отношением следования, а сумма и разность для них не определены.
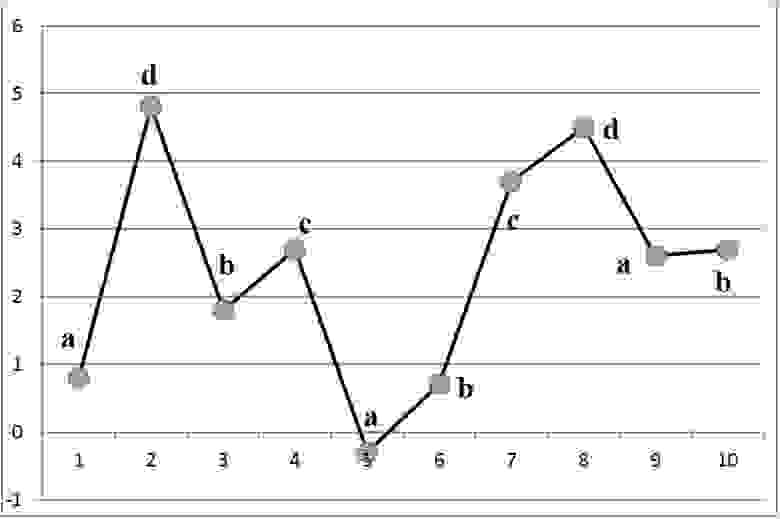
На рис. 5. представлен пример символьного локально-рангового кода для временного ряда. Несложно убедиться, что в пределах двух позиций слева и справа для каждого отсчета выборки символьная последовательность имеет те же соотношения, что и исходная. Для отсчетов, отстоящих более чем на 2 позиции, соотношения не выдерживаются (например, отсчеты с номерами 1 и 5), так как такие отсчеты полагаются несравнимыми.
Рис. 5. Символьное локально-ранговое кодирование.
Метод символьного локально-рангового кодирования был предложен в [3], а алгоритм его вычисления приведен в [4]. Вопросы локально рангового кодирования и его применения для оценивания энтропии сигналов подробно рассмотрены в монографии [5].
6. Работа с ранговыми данными
Как уже было сказано, над данными, представленными в ранговой шкале, арифметические операции не определены. Это, однако, не означает, что над этими данными совершенно запрещены такие операции, в определенных случаях их можно применить. Например, выполнить спектральный анализ для поиска скрытых периодичностей. Однако, так как информация о форме сигнала при кодировании потеряна, доверять можно только выявленной первой гармонике, вторая и последующие гармоники могут появиться вследствие нелинейности кодирования. Также возможно применение к ранговым данным корреляционного анализа.
Однако, так как ранговые данные являются, по существу, символьными к ним возможно абсолютно корректно применять следующие виды анализа:
7. Немного теории (и совсем скоро конец)
Ранговые коды обладают рядом интересных свойств, например, инвариантностью к непрерывным взаимно-однозначным преобразованиям. Так, ряды: x(n) и e^(x(n)) будут иметь совпадающие ранговые коды. Это делает их привлекательными, в частности, для решения задач оценивания энтропии временных рядов, поскольку оценки энтропии рядов типа x(n) и e^(x(n)) должны совпадать.
Но нам представляется, что шкальное кодирование найдет свое применение и в других областях, в частности Big Data. Обработка символьных последовательностей представляет собой хорошо разработанную область знаний и технологий, так что переход от числовых последовательностей к символьным позволяет расширить арсенал применяемых моделей и алгоритмов обработки.
Теоретические основы шкального кодирования данных вообще и временных рядов, в частности, должны лежать где-то в алгебре данных (вопрос авторами пока не проработан). Основная идея в том, что если мы исключаем из рассмотрения какие-либо свойства входных данных, полагая их незначимыми вследствие их природы либо особенностей процедуры измерения, то мы должны от представления числами переходить к представлению элементами множества с определенными на нем операциями и отношениями, соответствующими тем, которые допустимы для данных. Так, если мы говорим, что абсолютные значения разностей между отсчетами незначимы, и доверять можно только знакам этих разностей, то мы сразу получаем множество, изоморфное некоторому алфавиту символов.
Отказ от сравнимости удаленных друг от друга отсчетов приводит к частично упорядоченному множеству, в котором не все элементы сравнимы. Так что, строго говоря, для локально-рангового кода необходимо выбирать не алфавит (так как в нем все элементы сравнимы), а множество другого типа. Такими свойствами обладает, например, множество слов, упорядоченных отношением ≤, заданным таким образом, что слово А меньше слова Б в том и только том случае, если все буквы, входящие в А меньше, чем соответствующие буквы слова Б. Так слово cbg будет меньше, чем dhr (c