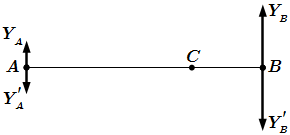что такое аксиомы статики твердого тела как они формулируются

Инструменты пользователя

Инструменты сайта

Боковая панель

Теория вероятностей и математическая статистика
Строительная механика для строительных специальностей
Матанализ. Дифференциальное и интегральное исчисление
economics

Теоретическая механика. Статика:

Контакты

Аксиомы статики

Система аксиом статики, о которой мы уже упоминали, была сформулирована И.Ньютоном в 1687 г. в его работе «Математические основы натуральной философии». Часть этих аксиом известна из школьного курса физики как законы Ньютона, хотя первый из них – закон инерции был сформулирован еще Г.Галилеем.

1. Аксиома инерции. Под действием уравновешенной системы сил тело движется прямолинейно и равномерно или находится в состоянии покоя.

2. Аксиома равновесия системы двух сил. Система двух сил уравновешена в том и только в том случае, если эти силы:

3. Аксиома присоединения или исключения уравновешенной системы сил. Действие системы сил на тело не изменится, если к ней присоединить (исключить из нее) уравновешенную систему сил.

Следствием этой аксиомы является следующая

Теорема 1. Действие силы на ТТ не изменится, если эту силу перенести вдоль линии действия в любую точку этого тела.

Тогда в силу аксиом 2 и 3:

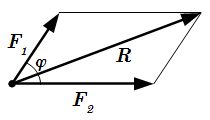
4. Аксиома параллелограмма. Равнодействующая двух пересекающихся сил приложена в точке пересечения их линий действия и изображается диагональю параллелограмма, построенного на этих силах как на сторонах.

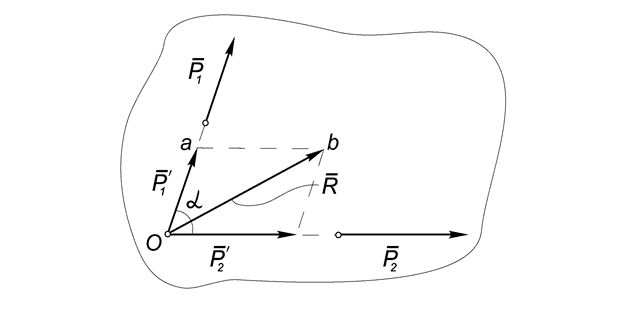
Отметим, что математически рассмотренная процедура определения равнодействующей соответствует нахождению суммы векторов (Рис.3):

Для определения модуля равнодействующей возведем последнее выражение в квадрат:

откуда получим искомое выражение:

$$R = \sqrt<^2 + ^2 + 2 P_1 P_2 \cos(\alpha)>$$

Построение параллелограмма можно, очевидно, заменить построением силового треугольника Oab.

Отметим, что эти силы в отличие от сил, о которых идет речь в аксиоме 2, системы не образуют, поскольку приложены к разным телам.

6. Аксиома отвердевания. Равновесие деформируемого тела не нарушится, если его считать абсолютно твердым.

Эта аксиома позволяет рассматривать равновесие не только абсолютно твердых, но также деформируемых тел и даже жидкости. Например – в гидростатике.

7. Аксиома освобождаемости от связей. Несвободное тело можно считать свободным, если вместе с активными силами приложить к нему реакции отброшенных связей.

Отметим, что во всех предыдущих аксиомах рассматривались свободные тела. Соответственно для свободных тел впоследствии будут получены условия равновесия и теоремы статики. В то же время все окружающие нас строительные конструкции и сооружения представляют собой примеры тел несвободных. Отсюда понятна значимость последней аксиомы, которая позволяет от несвободных тел переходить к свободным, а также необходимость умения определять реакции этих связей.

Источник

Теоретическая механика

2. Аксиомы статики

В основе учения о равновесии абсолютно твердых тел лежат некоторые эмпирические положения, которые называются постулатами или аксиомами. Эти аксиомы выражают те основные факты, которые дают нам опыт и наблюдения при изучении действия сил на абсолютно твердое тело.

Свободное абсолютно твердое тело (АТТ) под действием двух сил находится в равновесии тогда и только тогда, когда эти силы имеют общую линию действия, равны по модулю и направлены противоположно.

Данная аксиома по сути состоит из двух частей.

Первая часть. Если свободное абсолютно твердое тело (АТТ) под действием двух сил находится в равновесии, то эти силы имеют общую линию действия, равны по модулю и направлены противоположно.

Вторая часть. Если на абсолютно твердое тело (АТТ) действуют две равные по модулю, противоположно направленные и имеющие общую линию действия силы, то данное тело находится в состоянии равновесия.

Не изменяя действия данной системы сил на АТТ, можно прибавить к этой системе или отнять от нее две уравновешенные силы, то есть две силы, равные по модулю и направленные вдоль общей прямой в разные стороны.

Следствие к аксиоме №2.

Сила является скользящим вектором. Иначе говоря, не изменяя действия данной силы на АТТ, точку приложения этой силы можно переносить вдоль ее линии действия.

Доказательство. Доказательство проведем в несколько этапов.

Что и требовалось доказать.

Все три силы находятся в одной плоскости. Величину равнодействующей можно найти графически как длину диагонали параллелограмма или вычислить по теореме косинусов:

Данная аксиома допускает и обратное утверждение: силу можно разложить бесчисленным множеством способов на две силы.

При всяком действии одного материального тела на другое имеет место такое же по величине, противоположное по направлению и действующее по одной прямой противодействие.

Эту аксиому в динамике называют третьим законом Ньютона о равенстве действия и противодействия.

Аксиома №5. (Аксиома об освобождении от связей)

Любое несвободное тело можно освободить, заменяя связи силами реакции связей.

Аксиома №6. (Принцип отверждения).

Если деформируемое твердое тело (не абсолютно твердое тело) под действием некоторой системы сил находится в состоянии равновесия, то равновесие не нарушится, если тело считать абсолютно твердым.

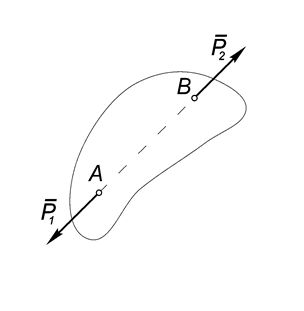
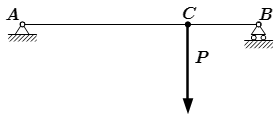
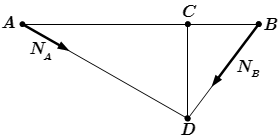
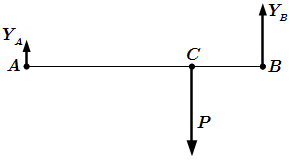
Невесомый стержень находится под действием сил и как показано на рис.С.4

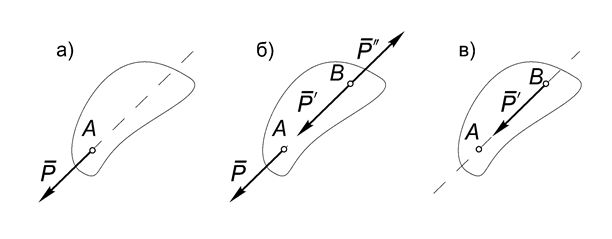
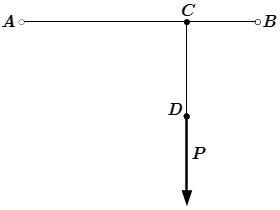
Перенесем силы вдоль линий действия в точку их пересечения.

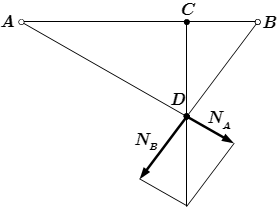
Сложим эти силы как показано на рисунке С.5.

Тогда вектор показывает направление уравновешивающей силы, а точка определяет положение точки приложения уравновешивающей силы.

Источник

Аксиомы статики

Условие применения аксиом

Аксиомы статики – это основные законы и правила, которые применяют при преобразовании систем сил в эквивалентные системы. Такие преобразования не меняют уравнений движения абсолютно твердых тел. Поэтому они позволяют перейти от исходной системы сил к более простой, под действием которой механическая система будет совершать такое же движение, как и при действии на нее исходной системы. Аксиомы статики применяются не только при рассмотрении неподвижных состояний тел, но и во многих других задачах теоретической механики, связанными с силовыми воздействиями. Условием их применения является условие отсутствия деформаций в телах, или малость деформаций по сравнению с размерами механической системы. При таком приближении все тела рассматриваются как абсолютно твердые. В тех задачах, в которых тела нельзя считать абсолютно твердыми, например, при рассмотрении деформаций, аксиомы статики применять нельзя.

С точки зрения логики изложения материала, было бы естественным сначала изучить основы динамики материальных тел, а уже затем изучать статику в качестве одного из ее подразделов – как частный случай движения с нулевой скоростью. Однако, в силу особой важности и большого числа задач, в которых применяются законы статики, ее часто изучают в самом начале как особую дисциплину. При этом основные правила статики излагают в виде аксиом – то есть положений, принятых без доказательств. Часть аксиом действительно являются фундаментальными законами механики, установленными в результате обобщения экспериментальных данных (аксиомы 1 и 5). Остальные являются следствиями уравнений движения твердых тел.

Аксиомы статики

1. Аксиома инерции (закон инерции Галилея)
Существуют такие системы отсчета, в которых любая материальная точка, не взаимодействующая с другими телами и точками, движется прямолинейно и равномерно. В частности, если тело покоилось в определенный момент времени, то оно будет покоиться и в последующие моменты.

Такие системы отсчета называются инерциальными. В механике, если это особо не оговорено, под системой отсчета подразумевается именно инерциальная система отсчета.

2. Аксиома равновесия двух сил
Две силы, приложенные к абсолютно твердому телу, являются уравновешенными тогда и только тогда, когда они равны по модулю, направлены в противоположные стороны и их линии действия совпадают.

3. Аксиома присоединения и исключения уравновешивающихся сил
Кинематическое состояние твердого тела не изменится, если к действующей на него системе сил прибавить или отнять уравновешенную систему сил.

То есть, прибавляя или исключая уравновешенную систему сил, мы получаем эквивалентную систему сил.

Следствие аксиом 2 и 3
Действие силы на твердое тело не изменится, если точку приложения силы перенести вдоль ее линии действия. То есть сила, приложенная к твердому телу, является скользящим вектором. Доказательство ⇓

4. Аксиома параллелограмма сил
Две силы, приложенные к телу в одной точке, можно заменить их равнодействующей силой, равной векторной сумме этих сил и приложенной к той же точке.
Верно и обратное. Любую силу можно разложить на две (и более) силы по правилу векторной суммы (по правилу параллелограмма), приложенных в той же точке, что и исходная сила.

Если две взаимодействующие точки принадлежат одному твердому телу, то их силы взаимодействия друг с другом образуют уравновешенную систему сил и, согласно аксиоме 3, могут быть исключены из рассмотрения. Однако, если эти точки принадлежат разным телам, то они не образуют уравновешенной системы. Поэтому исключать такое взаимодействие нельзя.

6. Принцип отвердевания
Если деформируемое тело находится в равновесии, то его равновесие не нарушится, если тело считать абсолютно твердым.

Принцип отвердевания указывает, что если конструкция, состоящая из подвижных частей, находится в равновесии (то есть скорости всех ее точек относительно некоторой инерциальной системы отсчета равны нулю), то уравнения равновесия можно применять ко всей конструкции в целом, считая ее единым твердым телом. Этот принцип является следствием предыдущих аксиом.

Применение аксиом к решению задач

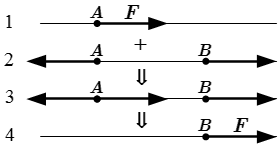
Наиболее эффективные способы решения задач статики основаны на применении уравнений равновесия. Однако, такие задачи можно решать, применяя только аксиомы. В некоторых случаях это даже является преимуществом, поскольку такое решение является графическим. Далее мы приводим правила, основанные на аксиомах статики, применяемые при решении задач графическим способом.

При графическом решении задач статики, исходную систему сил заменяют эквивалентной, применяя следующие действия.

Далее мы рассмотрим пример решения задачи с помощью аксиом статики.

Задача

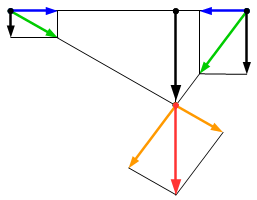
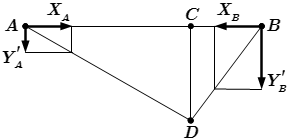
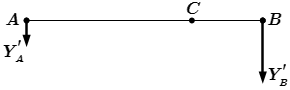
1.4. Раскладываем каждую из сил и на две составляющие – горизонтальную и вертикальную:
;
.

Выполняя решение графическим способом, мы получили небольшую погрешность. Но нашей целью было наглядно продемонстрировать применение аксиом статики к решению задач.

Доказательство следствия аксиом 2 и 3

Докажем, что из аксиом 2 ⇑ и 3 ⇑ следует, что точку приложения силы можно перемещать вдоль линии ее действия.

Использованная литература:
А. А. Яблонский, В.М. Никифорова. Курс теоретической механики, часть 1, статика, кинематика. Москва, «Высшая школа», 1966.
Г. Н. Яковенко. Краткий курс теоретической механики. Москва, 2005.

Источник

Тема 1.1. Основные понятия и аксиомы статики

§1. Элементы векторной алгебры

В теоретической механике рассматриваются такие векторные величины как сила, моменты силы относительно точки и оси, момент пары сил, скорость, ускорение и другие.

1. Понятие вектора.

Операции над векторами. Вектора можно складывать и умножать на число.

— сумма двух векторов есть вектор

— существует нулевой вектор

Рис.1. Сложение векторов

В математике все вектора являются свободными, их можно переносить параллельно самим себе.

В сумме двух векторов (рис.1,а) начало второго вектора можно поместить в конец первого вектора, тогда сумму двух векторов можно представить как вектор, имеющий начало в начале первого вектора, а конец в конце второго вектора. Применяя это правило для суммы нескольких векторов (рис.1,б) получаем, что суммой нескольких векторов является вектор замыкающий ломаную линию, состоящую из слагаемых векторов.

Операции над векторами подчиняются следующим законам (см. рис.2):

Рис.2. Операции над векторами

2. Проекцией вектора на ось

Проекцией вектора на ось называется скалярная величина, которая определяется отрезком, отсекаемым перпендикулярами, опущенными из начала и конца вектора на эту ось. Проекция вектора считается положительной (+), если направление ее совпадает с положительным направлением оси, и отрицательной (-), если проекция направлена в противоположную сторону (см. рис.3).

Рис.3. Проекция вектора на ось

§2. Основные понятия статики

Статикой называется раздел механики, в котором излагается общее учение о силах и изучается условия равновесия материальных тел, находящихся под действием сил.

Твердое тело. В статике и вообще в теоретической механике все тела считаются абсолютно твердыми. То есть предполагается, что эти тела не де­формируются, не изменяют свою форму и объем, какое бы действие на них не было оказано. Материальной точкой будет называться абсолютно твердое тело, размерами которого можно пренебречь.

Под равновесием будем понимать состояния покоя тела по отношению к другим материальным телам.

1. Величина, являющаяся количественной мерой механического взаимодействия материальных тел, называется в механике силой.

В Международной системе единиц (СИ) силу измеряют в ньютонах (Н), килоньютонах (кН). Сила является величиной векторной.

Ее действие на тело опре­деляется:

1) численной величиной или модулем силы

2) направле­нием силы

3) точкой приложения силы (рис.4).

Рис.4. Сила, приложенная к телу

Силу, как и другие векторные величины, изображают в виде направленного отрезка со стрелкой на конце, указывающей его направление.

Прямая DE, вдоль которой направлена сила, называется линией действия силы.

Понятия «линия действия» и «направление» близки, но не тождественны. Очевидно, что по линии действия можно определить направление с точностью до противоположного. Аналогично связаны понятия «модуль» и «величина» для вектора.

2. Совокупность сил, действующих на какое-нибудь твердое тело, будем называть системой сил. Предполагается, что действие силы на тело не изменится, если ее перене­сти по линии действия в любую точку тела (конечно – твердого тела). Поэтому вектор силы называют скользящим вектором. Если силу перенести в точку, не расположенную на этой линии, действие ее на тело будет совсем другим.

3. Тело, не скрепленное с другими телами, которому из данного положения можно сообщить любое перемещение в пространстве, на­зывается свободным.

4. Если одну систему сил, действующих на свободное твердое тело, можно заменить другой системой, не изменяя при этом состоя­ния покоя или движения, в котором находится тело, то такие две системы сил называются эквивалентными.

Например, если системы сил, изображенных на рис. 5, а и рис. 5, б, уравновешены, то эти две системы сил будут эквивалентны друг другу.

Рис 5. Система сил:

а – заданная система сил; б – эквивалентная система сил

5. Система сил, под действием которой свободное твердое тело может находиться в покое, называется уравновешенной или экви­валентной нулю.

7. Сила, равная равнодействующей по модулю, прямо противополож­ная ей по направлению и действующая вдоль той же прямой, назы­вается уравновешивающей силой.

8. Силы, действующие на твердое тело, можно разделить на внешние и внутренние. Внешними называются силы, действующие на частицы данного тела со стороны других материальных тел. Внутренними называются силы, с которыми частицы данного тела действуют друг на друга.

9. Сила, приложенная к телу в какой-нибудь одной его точке, называется сосредоточенной.

Силы, действующие на все точки дан­ного объема или данной части поверхности тела, называются распре­деленными.

Понятие о сосредоточенной силе является условным, так как практически приложить силу к телу в одной точке нельзя. Силы, которые мы в механике рассматриваем как сосредоточенные, пред­ставляют собою по существу равнодействующие некоторых систем распределенных сил.

В частности, обычно рассматриваемая в механике сила тяжести, действующая на данное твердое тело, представляет собою равно­действующую сил тяжести его частиц. Линия действия этой равно­действующей проходит через точку, называемую центром тяжести тела.

§3. Аксиомы статики

Все теоремы и уравнения статики выво­дятся из нескольких исходных положений, принимаемых без матема­тических доказательств и называемых аксиомами или принципами статики. Аксиомы статики представляют собою результат обобщений многочисленных опытов и наблюдений над равновесием и движением тел, неоднократно подтвержденных практикой. Часть из этих аксиом является следствиями основных законов механики, с которыми мы познакомимся в динамике.

Аксиома 1. Если на свободное абсолютно твердое тело действуют две силы, то тело может находиться в равновесии тогда и только тогда, когда эти силы равны по модулю (F₁ = F₂) и направлены вдоль одной прямой в противоположные стороны (рис. 6).

Рис.6. Система сил, находящаяся в равновесии

Аксиома 1 определяет простейшую уравновешенную систему сил, так как опыт показывает, что свободное тело, на которое действует только одна сила, находиться в равнове­сии не может.

Аксиома 2. Действие данной си­стемы, сил на абсолютно твердое тело не изменится, если к ней прибавить или от нее отнять уравновешенную систему сил.

Эта аксиома устанавливает, что две системы сил, отличающиеся на уравнове­шенную систему, эквивалентны друг другу.

Следствие из 1-й и 2-й аксиом. Действие силы на абсо­лютно твердое тело не изменится, если перенести точку при­ложения силы вдоль ее линии действия в любую другую точку тела.

Рис.7. Система сил

В самом деле, пусть на твердое тело действует приложенная в точке А сила (рис.7). Возьмем на линии действия этой силы произвольную точку В и приложим к ней две уравновешенные силы

Аксиома 3 (аксиома параллелограмма сил). Две силы, приложенные к телу в одной точке, имеют равнодействующую, приложенную в той же точке и изображаемую диагональю па­раллелограмма, построенного на этих силах, как на сторонах.

Рис.8. Равнодействующая двух сил

Следовательно, аксиому 3 можно еще формулировать так: две силы, приложенные к телу в одной точке, имеют равнодействую­щую, равную геометрической (векторной) сумме этих сил и прило­женную в той же точке.

Аксиома 4 (принцип противодействия). При всяком действии одного материального тела на другое имеет место такое же по величине, но проти­воположное по направлению противодействие.

(рис. 9). Однако силы и не образуют урав­новешенной системы сил, так как они приложены к разным телам. Эта аксиома соответствует третьему закону Ньютона: действие всегда равно и противоположно противодействию. При этом необходимо помнить, что в аксиоме 4 рассматривается случай, когда силы приложены к разным телам и в этом случае система сил не является уравновешенной в отличие от случая действия сил в аксиоме 2.

Рис.9. Противодействие

Рис. 10. Опирание балки на опоры:

а – схема загружения балки; б – силы действия балки на

опоры и противодействия со стороны опор на балку

Аксиома 5 (принцип отвердевания). Равновесие изме­няемого (деформируемого) тела, находящегося под действием дан­ной системы сил, не нарушится, если тело считать отвердевшим (абсолютно твердым). Из принципа отвердения следует, что условия, необходимые и достаточные для равновесия абсолютно твердого тела, необходимы, но не достаточны для равновесия деформируемого тела, по форме и размерам тождественного с данным.

Высказанное в этой аксиоме утверждение очевидно. Например, ясно, что равновесие цепи не нарушится, если ее звенья считать сва­ренными друг с другом и т. д.

Аксиома 6 (аксиома связей). Всякое несвободное тело можно рассматривать как свободное, если механическое действие связей заменить реакциями этих связей (пояснения к этой аксиоме в следующем параграфе).

Приведенные принципы и аксиомы положены в основу методов решения задач статики. Все они широко используются в инженерных расчетах.

Видео-урок «Аксиомы статики»

§4. Связи и их реакции

По определению, тело, которое не скреплено с другими телами и может совершать из данного положе­ния любые перемещения в пространстве, называется свободным (например, воздушный шар в воздухе). Тело, перемещениям которого в пространстве препятствуют какие-нибудь другие, скрепленные или соприкасающиеся с ним тела, называется несвободным. Все то, что ограничивает перемещения данного тела в пространстве, будем называть связью.

Например, тело лежащее на столе – несвободное тело. Связью его является плоскость стола, которая препятствует перемещению тела вниз.

Очень важен так называемый принцип освобождаемости, которым будем пользоваться в дальнейшем. Записывается он так:

Любое несвободное тело можно сделать свободным, если связи убрать, а действие их на тело заменить силами, такими, чтобы тело оставалось в равновесии.

Сила, с которой данная связь действует на тело, препятствуя тем ила иным его перемещениям, называется силой реакции (противодействия) связи или просто реакцией связи.

Так у тела, лежащего на столе, связь – стол. Тело несвободное. Сделаем его свободным – стол уберем, а чтобы тело осталось в равнове­сии, заменим стол силой, направленной вверх и равной, конечно, весу тела.

Направлена реакция связи в сторону, противоположную той, куда связь не дает перемещаться телу. Когда связь одновременно препятствует перемещениям тела по нескольким направлениям, направление реакции связи также наперед неизвестно и должно определяться в результате решения рассматриваемой задачи.

Если в качестве физического тела рассматривать какой-либо элемент инженерного сооружения (балка, ферма, колонна, плита и т. п.), который передает давление на опоры, то реакции опор (связей) называют опорными реакциями. Реакции связей носят вторичное происхождение, они возникают как противодействие другим силам.

Все силы, кроме реакции связей, называют заданными силами. Термин «заданные силы» имеет глубокий смысл. Заданные силы чаще всего являются активными, т.е. силами, которые могут вызвать движение тел, например: сила тяжести, снеговая или ветровые нагрузки и т.п. Учитывая сказанное выше, будем подразделять силы на активные силы и реакции связей.

Для определения направления реакции необходимо установить особенности взаимодействия твердого тела со связями различного вида. Следует иметь в виду, что реакция всегда направлена противоположно направлению возможного перемещения тела при удалении связи.

Рассмотрим, как направлены реакции некоторых основных видов связей:

1. Гладкая плоскость (поверхность) или опора. Гладкой будем называть поверхность, трением о которую данного тела можно в первом приближении пренебречь. Такая поверхность не дает телу перемещаться только по направлению общего перпен­дикуляра (нормали) к поверхностям соприкасающихся тел в точке их касания (рис.11, а). Поэтому реакция N гладкой поверхности или опоры направлена по общей нормали к поверхностям сопри­касающихся тел в точке их касания и приложена в этой точке. Когда одна из соприкасающихся поверхностей является точкой (рис. 11, б), то реакция направлена по нормали к другой поверх­ности.

Источник