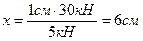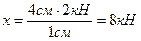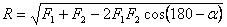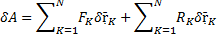что такое активные силы в технической механике

Активные и реактивные силы

ОСНОВНЫЕ ПОНЯТИЯ И АКСИОМЫ СТАТИКИ

Лекция №1

ТЕОРЕТИЧЕСКАЯ МЕХАНИКА

Теоретическая механика – это наука, изучающая математические методы расчёта механизмов и сооружений. Расчет ведется не самих реальных объектов, а их моделей. Применяют графический и аналитический методы расчета.

Графический метод –основан на геометрических построениях.

Аналитический метод –основан на алгебраических расчетах.

Статика – это раздел теоретической механики, который изучает равновесие абсолютно твердых тел под действием сил.

Абсолютно твердое тело – это недеформируемое тело, в котором расстояние между любыми двумя точками всегда остается неизменным и никакие внешние воздействия не вызывают изменения его размеров и формы.

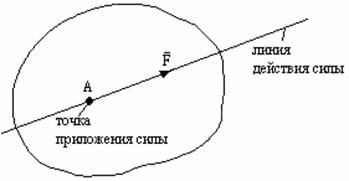
Сила – это мера механического воздействия одного тела на другое. Сила измеряется в ньютонах(Н) и является векторной величиной, то есть характеризуется 1) численным значением (модулем);

2) точкой приложения;

В графическом методе расчета силу изображают в виде вектора, в каком либо масштабе.

Пример1.1. Начертить вектор силы F = 30 кН в масштабе 1:5.

Решение. Составляем пропорцию:

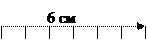
Пример 1.2. Определить значение силы, если в масштабе 1:2 вектор имеет длину 3 см.

Решение: составляем пропорцию:

Силы бывают внешними и внутренними.

Внешние силы представляют собой действие одного тела на другое и

делятся на активные и реактивные.

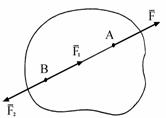
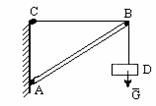
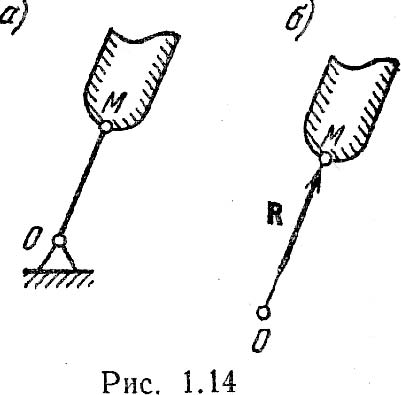
Активные силы – стремятся вызвать перемещение тела (сила G, рис. 1.1).

Реактивные силы (реакции) – стремятся противодействовать перемещению тела под действием активных сил (сила R, рис. 1.1).

Внутренние силы — возникают внутри тела под действием внешних сил.

Система сил— совокупность нескольких сил, прило­женных к телу.

Плоская система сил — линии действия сил лежат в одной плоскости.

Пространственная система сил — линии действия сил лежат в разных пло­скостях.

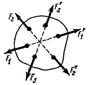
Сходящаяся система сил линии действия сил пересекаются в одной точке (рис. 1.2).

Эквивалентные системы сил – разные системы сил, которые ока­зывают одинаковое механическое действие на тело.

Равнодействующая сила — одна сила, эквивалентная данной системе сил.

Уравновешивающая сила — сила, равная по модулю данной силе и направленная по той же линии действия, но в проти­воположную сторону.

Уравновешенная система сил — система сил, приложенная к материальной точке под воздействием которой точка находится в со­стоянии покоя.

Правило параллелограмма — равнодействующая (F_Σ) двух сил (F₁ и F₂), приложенных к одной точке, является диагональю параллелограмма, построенного на данных силах/Вместо правила параллелограмма можно пользоваться правилом треугольника.

Вопрос

Основные понятия и аксиомы статики

Материальной точкой называют тело, размерами которого можно пре-небречь. Она обладает массой и способностью взаимодействовать с другими материальными точками. Например, в небесной механике планеты, движущие-ся вокруг Солнца, часто рассматривают как материальные точки, поскольку их размеры малы по сравнению с размерами орбит. Пользоваться понятием мате-риальной точки целесообразно также и в том случае, когда все частицы движу-щегося физического тела перемещаются одинаково.

Совокупность материальных точек, положения и движения которых взаимосвязаны между собой, называется системой материальных точек.

В теоретической механике пренебрегают малыми деформациями тел и считают эти тела абсолютно твердыми.

Абсолютно твердым телом называется такое тело, расстояние между дву-мя точками которого, во все время движения, остается величиной постоянной.

Силой называется количественная мера механического взаимодействия тел. Сила является векторной величиной, действие силы на тело определяется численным значением (модулем), направлением и точкой приложения силы
(рис. 1.1).

На схемах сила изображается направленным отрезком. Основной едини-цей измерения силы является 1 Ньютон (1Н).
— Совокупность нескольких сил, действующих на тело, называется систе-мой сил.
— Эквивалентные системы сил — системы сил, оказывающие одинаковое механическое действие на одно и то же тело.
— Уравновешенная система сил — система сил, под действием которой те-ло находится в равновесии.
— Сила, эквивалентная некоторой системе сил, называется равнодействующей.
— Сила, равная по модулю равнодействующей и направленная по линии ее действия в противоположную сторону, называется уравновешивающей силой.
— Внешними силами называются силы, действующие на тело со стороны других тел.
— Внутренние силы — силы взаимодействия между частицами одного и то-го же тела.
В статике рассматриваются условия равновесия внешних сил.

Аксиомы статики.В основе статики лежат несколько не требующих до-казательства аксиом, из которых выводятся все теоремы и уравнения.

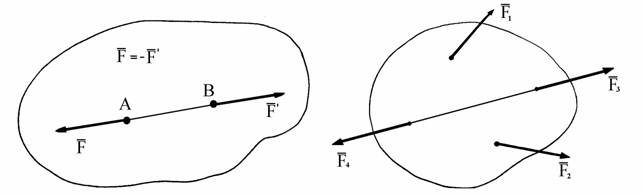
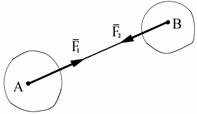
Аксиома 1. Две силы, действующие на абсолютно твердое тело уравновешива-ются только тогда, когда они равны по величине и направлены по од-ной прямой в противоположные стороны (рис. 1.2).

Рис. 1.2 Рис. 1.3Аксиома 2. Действие данной системы сил на абсолютно твердое тело не изме-нится, если прибавить к ней или отнять от нее уравновешенную сис-тему сил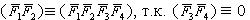
(рис. 1.3).

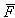
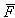
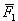
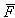
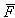
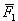
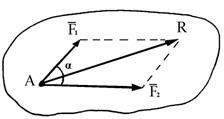
Следствие из аксиомы 1 и 2. Действие силы на абсолютно твердое тело (АТТ) не изменится, если точку приложения этой силы перенести по ли-нии ее действия. Пусть на тело в точке А действует сила (рис. 1.4). Добавим в точке В, выбранной произвольно на линии действия си-лы , уравновешенную систему сил и равных по абсолютной величине и направленных по линии ее действия. На основании аксиомы 1 силы и будут уравновешены и их можно отбросить (аксиома 2). В результате получим силу = , но приложенную не в точке А, а в точке В. Отсюда следует, что сила, приложенная к АТТ, есть вектор скользящий.

Рис. 1.4 Рис. 1.5 Рис. 1.6 Аксиома 3 Равнодействующая двух сил, приложенных к АТТ в одной точке, равна их геометрической сумме 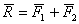, т.е. выражается по моду-лю и направлению диагональю параллелограмма,построенного на этих силах (рис. 1.5).

Аксиома 4 Всякому действию одного тела на другое соответствует равное по величине, но противоположное по направлению противодействие. Действие и противодействие-это силы, приложенные к двум раз-личным телам, поэтому они не уравновешиваются (рис. 1.6). Аксиома 5 Если деформируемое тело под действием системы сил находится в равновесии, то при отвердевании его равновесие сохраняется. Под действием сил тело D находится в равновесии. Если трос CB заменить стержнем, то равновесие не нарушится, равновесие не нарушится и в том случае, если трос BD за-менить стержнем, если же стержень АВ заменить тросом — равновесие нарушится (рис. 1.7).

Рис.1.7

Связи и их реакции. Твердое тело называется свободным, если оно мо-жет перемещаться в пространстве в любом направлении (ВС в полете). Тело, ограничивающее свободу движения данного твердого тела, является по отно-шению к нему связью. Твердое тело, свобода движения которого ограничена связями, называетсянесвободным (движение самолета по ВПП). Сила, с которой связь действует на тело, препятствуя его перемещению в том или ином направлении, называется силой реакции этой связи. Для нахождения реакции связей используют аксиому связей, на основании ко-торой всякое несвободное тело можно рассматривать как свободное, если от-бросить связи, заменив их действие на тело силами реакций этих связей. Направление силы реакции связи противоположно тому направлению, в котором активные силы стремятся переместить тело.

Различают три группы связей:

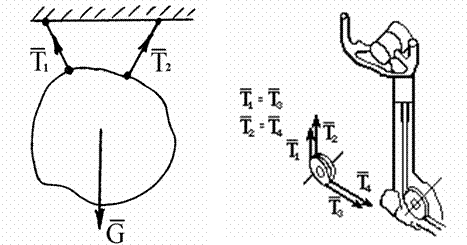
1. Гибкие связи (трос, цепь, ремень, канат). Реакции связей направлены по оси связей (рис. 1.8).

Рис. 1.8Если нить отклоняется роликом, в котором не учитывается трение, то натя-жение нити не изменяется. Например, натяжение тросов, идущих от штурвала к элеронам самолета, с обеих сторон равны по модулю |Т1|= |Т3|, |Т2|= |Т4| (рис. 1.8б). 2. Твердые, идеально гладкие связи. Реакция направлена по общей нор-мали к поверхностям соприкасающихся тел (рис. 1.9).

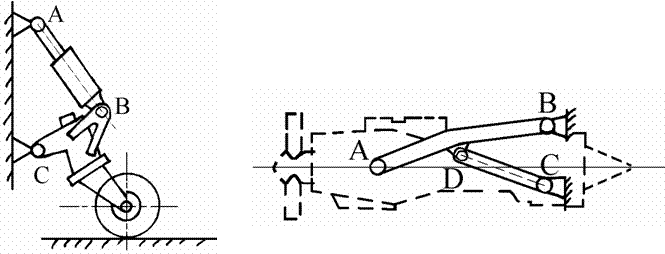
Рис. 1.93. Шарнирные связи. Шарниром в механике называется устройство, до-пускающее поворот одного телаотносительно другого, но ограничивающее при этом линейные перемещения этих тел. Шарнирами, например, являются соеди-нения А, В, С элементов задней опоры самолета (рис. 1.10), узлы А,В,С,D под-вески авиационного двигателя (рис. 1.11).

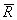
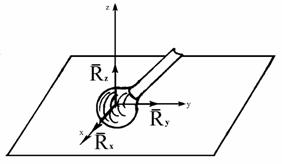
Реакция цилиндрического шарнира может иметь любое направление в плоскости, перпендикулярной оси шарнира. Направление реакции зависит от ве-личины и направления действующих на тело сил. Реакция подвижного шарнира всегда направлена по нормали к опорной поверхности шарнира (рис. 1.12б, в).

Рис. 1.12 Шаровой шарнир исключает любое перемещение тела во всех направле-ниях, кроме вращения, поэтому реакция шарового шарнира может иметь любое направление в пространстве. Чаще всего эту реакцию представляют в виде трех ее составляющих по осям координат x, y, z (рис. 1.13).

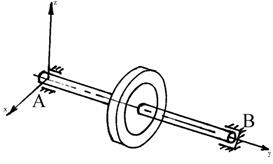
Рис. 1.13 Рис. 1.14 Разнообразные опорные устройства валов машин схематически представ-ляют подшипниками двух типов:радиальным (цилиндрическим — А), не пре-пятствующим некоторым осевым смещениям вала и радиально-упорным (В), исключающим осевые перемещения вала (рис. 1.14). Неподвижная защемляющая опора или жесткая заделка. На заделанный конец балки со стороны опоры действует система распределенных сил, кото-рую заменяем эквивалентной системой сосредоточенных сил и моментом Ма, приложенных в точке А (рис. 1.15).

Рис. 1.15 2 Вопрос

Активные силы и реакции связей.

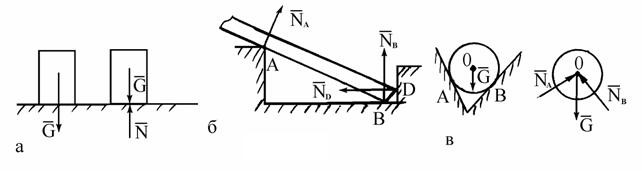
Тело назыв свободным, если его перемещения ничем не ограничены. Тело, перемещения которого ограничены другими телами, называется несвободным, а тела, ограничивающие перемещения данного тела,– связями.В точках контакта возникают силы взаимодействия между дан­ным телом и связями. Силы, с которыми связи действуют на данное тело, назы­ваются реакциями связей.

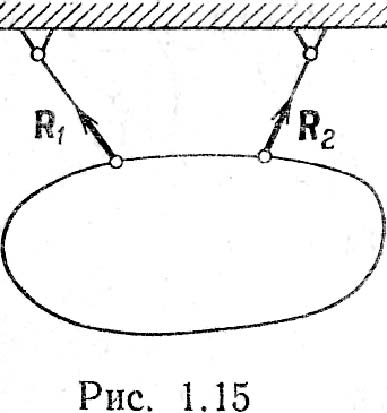
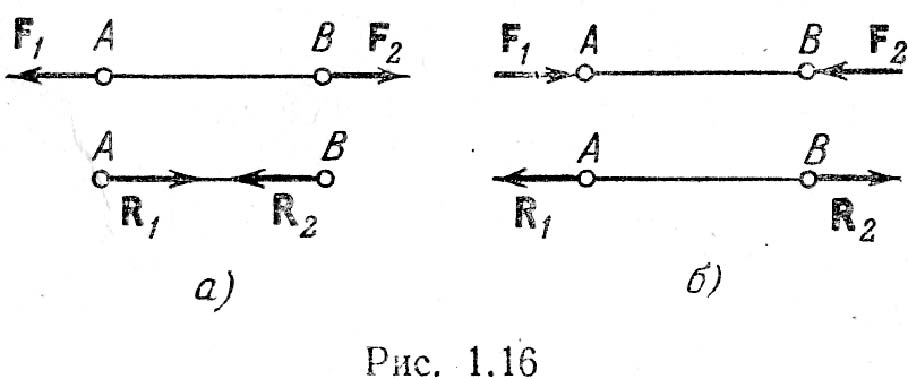
Принцип освобождаемоcти: всякое несвободное тело можно рассматривать как свободное, если действие связей заменить реакциями их, приложенными к данному телу.В статике полностью определить реакции связей можно с по­мощью условий или уравнений равновесия тела, которые будут установлены в дальнейшем, но направления их во многих случаях можно определить из рассмотрения свойств связей. В качестве простейшего примера на рис. 1.14, а представлено тело, точка М которого соединена с неподвижной точкой О при помощи стержня, весом которого можно пренебречь; концы стержня имеют шарниры, допускающие свободу вращения. В данном случае для тела связью служит стержень ОМ; стеснение свободы перемещения точки М выражается в том, что она вынуждена находиться на неизменном удалении от точки О. Сила действия на такой стержень должна быть направлена по прямой ОМ, и согласно аксиоме 4 сила противодей­ствия стержня (реакция) R должна быть направлена вдоль той же прямой. Т. о., направление реакции стержня совпадает с прямой ОМ (рис. 1.14, б). Аналогично сила реакции гибкой нерастя­жимой нити должна быть направлена вдоль нити. На рис. 1.15 показано тело, висящее на двух нитях, и реакции нитей R₁ и R₂. Силы, действующие на несвободное тело, делят на две категории. Одну кате­горию образуют силы, не зависящие от связей, а другую– реакции связей. При этом реакции связей носят пассив­ный характер– они возникают потому что на тело действуют силы первой категории. Силы, не зависящие от связей, называют активными, а реакции связей– пассивными силами. На рис. 1.16, а вверху показаны две равные по модулю активные силы F₁ и F₂, растягивающие стержень АВ, внизу показаны реак­ции R₁ и R₂ растянутого стержня. На рис. 1.16, б вверху показаны активные силы F₁ и F₂, сжимающие стержень, внизу показаны реакции R₁ и R₂сжатого стержня.

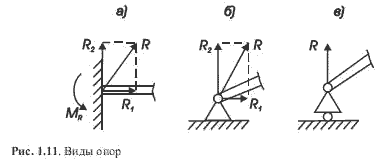
Виды опор

При решении плоской задачи считается, что всякий элемент имеет 3 степени свободы (3 возможных перемещения, однозначно определяющих положение тела в пространстве): вращение вокруг точки и 2 линейных перемещения вдоль 2-х осей).
Всякая реакция возникает в местах наложения связен.
Если наложено ограничение на одно из указанных выше перемещений (чаше всего перемещение полагается равным нулю), то в этом направлении возникает реакция опоры: сосредоточенная сила при ограничении линейного перемещения и пара сил при ограничении углового перемещения.
В зависимости от налагаемых ограничений на перемещение тела различают следующие виды опор:

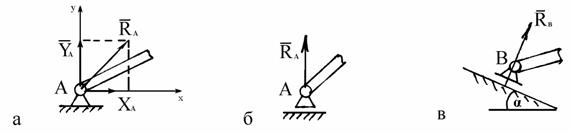
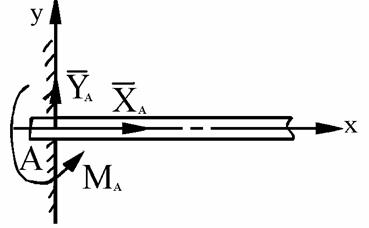
Заделка— нет перемещений (жесткое закрепление тела, например, сварка), возникают реакция неизвестной величины и направления R и реактивный момент M_R.
Неизвестную реакцию удобно представить в виде ее проекций на оси координат любого направления, например, для плоской системы горизонтальное и вертикальное. Итого: в плоской заделке возникают 3 неизвестные реакции — 2
силы и одна пара сил (рис. 1.11, а);

Неподвижная шарнирная опора— возможно вращение вокруг опоры, линейных перемещений нет, поэтому возникает реакция неизвестной величины и направления R, которую заменяют ее проекциями на оси координат. Для плоской системы возникают 2 неизвестные реакции: R₁ и R₂(рис. 1.11, б).
Примером шарнирной опоры можно считать подшипниковую опору. Внутреннее кольцо шарикового или роликового подшипника может поворачиваться относительно наружного на угол 2°. Этого достаточно, чтобы считать подшипник шарнирной опорой.

Подвижная шарнирная опора— возможно вращение вокруг опоры и перемещение вдоль одной из осей, например, плавающая подшипниковая опора, возникает одна реакция R: сила в направлении ограничения движения (перпендикулярно направлению движения вдоль оси) (рис. 1.11, в).

Внешние силы

Внешняя сила — это мера взаимодействия между телами. В задачах сопротивления материалов внешние силы считаются всегда заданными. К внешним силам относятся также реакции опор (связей).

Все внешние нагрузки можно разделить на статические и динамические.
Статическими считаются нагрузки, в процессе приложения которых возникающие силы инерции малы и ими можно пренебречь.
Если силы инерции велики (к примеру – землетрясение) – нагрузки считаются динамическими. Примерами таких нагрузок также могут служить внезапно приложенные нагрузки, ударные и повторно-переменные.
Внезапно приложенные нагрузки передаются на сооружение сразу
полной своей величиной (к примеру давление колес локомотива, входящего на мост).
Ударные нагрузки возникают при быстром изменении скорости соприкасающихся элементов конструкции, например» при ударе бабы копра о сваю при ее забивке.
Повторно-переменные нагрузки действуют на элементы конструкции, повторяясь значительное число раз. Таковы, например, повторные давления пара, попеременно растягивающие и сжимающие шток поршня и шатун паровой машины. Во многих случаях нагрузка представляет собой комбинацию нескольких видов динамических воздействий.

Внутренние силы

В результате действия внешних сил в теле возникают внутренние силы.
Внутренняя сила — силы взаимодействия между частями одного тела, возникающие под действием внешних сил.

Внутренние силы являются самоуравновешенными, поэтому они не видны и не влияют на равновесие тела. Определяют внутренние силы методом сечения.

Внешние нагрузки приводят к следующим видам напряженно-деформированного состояния:

Активные и реактивные силыявляются внешними силами ( нагрузками), вызывающими деформацию изгиба в балке.

Принцип Даламбера формулируется так: активные и реактивные силы, действующие на материальную точку, вместе с силами инерции образуют систему взаимно уравновешенных сил, удовлетворяющую всем условиям равновесия.

Как было сказано выше, внешними нагрузками балки являютсяактивные и реактивные силыи моменты.

Решая задачу первым способом, мы учитывали только фактически действующие на телоактивные и реактивные силы и составили шесть всеобщих уравнений движения, связывающих проекции этих сил с массами и с проекциями ускорений частиц тела.

Для определения внутренних силовых факторов применим метод сечений, причем изображать балку будем только одной линией — осью, к которой приложеныактивные и реактивные силы.

Пусть всеактивные и реактивные силы и массы механизма приведены к одному из его звеньев.

Расчеты с учетом инерционных нагрузок ведутся известным из теоретической механики методом кинетостатики, основанном на принципе Даламбера. Согласно этому принципу всеактивные и реактивные силы, приложенные к телу, вместе с силами инерции образуют систему взаимно уравновешенных сил, удовлетворяющую всем условиям равновесия. Таким образом, задачи динамики и сопромата решаются методами статики.

Возможная работа — элементраная работа силы на возможном перемещении.

dA=Fdr — элементарная работа силы (F и r — векторы)

Если у какой-то связи 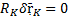(R_K тоже вектор), то связь называется идеальной.

Если вся сумма 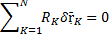, то механическая система с идеальными связями.

Примеры идеальных связей: внутренние связи в абсолютно твердых телах; абсолютно гладкие поверхности; шарниры без трения; нерастяжимые нити; закрепленные точки; качение без скольжения.

Примеры идеальных связей:

1. Наложенная на материальную точку связь в виде гладкой поверхности (неподвижной или деформирующейся с течением времени), по которой должна двигаться точка (здесь возможные перемещения лежат в касательной плоскости к данной поверхности, а реакция связи этой плоскости ортогональна, так что скалярное произведение равно нулю).

2. Внутренние связи в абсолютно твёрдом теле, обеспечивающие постоянство расстояний между текущими положениями точек тела.

3. Контакт двух абсолютно твёрдых тел, соприкасающихся при движении гладкими поверхностями.

4. Контакт двух абсолютно твёрдых тел, соприкасающихся при движении абсолютно шероховатыми поверхностями.

Источник

Что такое активные силы в технической механике

Теоретическая механика – это наука о механическом движении твердых материальных тел и их взаимодействии. Механическое движение понимается как перемещение тел в пространстве и во времени по отношению к другим телам, в частности, к Земле.

Статика изучает условия равновесия тел под действием сил.

Кинематика рассматривает движение тел как перемещение в пространстве; характеристики тел и причины, вызывающие движение, не рассматриваются.

Динамика изучает движение тел под действием сил.

Сила – это мера механического взаимодействия материальных тел между собой. Взаимодействие характеризуется величиной и направлением, т. е. сила – это величина векторная, характеризующаяся точкой приложения, направлением (линией действия), величиной (модулем).

Силы, действующие на тело (или систему сил), делят на внешние и внутренние. Внешние силы бывают активные и реактивные. Активные силы вызывают перемещение тела, реактивные стремятся противодействовать перемещению тела под действием внешних сил.

Системой сил называют совокупность сил, действующих на тело.

Эквивалентная система сил – система сил, действующая так же, как заданная.

Уравновешенной (эквивалентной нулю) системой сил называется такая система, которая, будучи приложенной к телу, не изменяет его состояния.

Систему сил, действующих на тело, можно заменить одной равнодействующей, действующей так, как система сил.

Все теоремы и уравнения статики выводятся из нескольких исходных положений, называемых аксиомами.

Первая аксиома. Под действием уравновешивающей системы сил абсолютно твердое тело или материальная точка находятся в равновесии или движутся равномерно и прямолинейно (закон инерции).

Вторая аксиома. Две силы, равные по модулю и направленные по одной прямой в разные стороны, уравновешиваются.

Третья аксиома. Не нарушая механического состояния тела, можно добавить или убрать уравновешивающую систему сил (принцип отбрасывания системы сил, эквивалентной нулю).

Четвертая аксиома (правило параллелограмма сил). Равнодействующая двух сил, приложенных к одной точке, приложена к той же точке и является диагональю параллелограмма, построенного на этих силах как на сторонах.

Пятая аксиома. При взаимодействии тел всякому действию соответствует равное и противоположно направленное противодействие.

Следствие из второй и третьей аксиом. Силу, действующую на твердое тело, можно перемещать вдоль линии ее действия.

2. Связи и реакции связей

Все тела делятся на свободные и связанные.

Свободные тела – это тела, перемещение которых не ограничено.

Связанные тела – это тела, перемещение которых ограничено другими телами.

Тела, ограничивающие перемещение других тел, называют связями.

Силы, действующие от связей и препятствующие перемещению, называют реакциями связей. Реакция связи всегда направлена с той стороны, куда нельзя перемещаться.

Всякое связанное тело можно представить свободным, если связи заменить их реакциями (принцип освобождения от связей).

Связи делятся на несколько типов.

Связь – гладкая опора (без трения) – реакция опоры приложена в точке опоры и всегда направлена перпендикулярно опоре.

Гибкая связь (нить, веревка, трос, цепь) – груз подвешен на двух нитях. Реакция нити направлена вдоль нити от тела, при этом нить может быть только растянута.

Жесткий стержень – стержень может быть сжат или растянут. Реакция стержня направлена вдоль стержня. Стержень работает на растяжение или сжатие. Точное направление реакции определяют, мысленно убрав стержень и рассмотрев возможные перемещения тела без этой связи.

Возможным перемещением точки называется такое бесконечно малое мысленное перемещение, которое допускается в данный момент.

Шарнирная опора. Шарнир допускает поворот вокруг точки закрепления. Различают два вида шарниров.

Подвижный шарнир. Стержень, закрепленный на шарнире, может поворачиваться вокруг шарнира, а точка крепления может перемещаться вдоль направляющей (площадки). Реакция подвижного шарнира направлена перпендикулярно опорной поверхности, так как не допускается только перемещение поперек опорной поверхности.

Неподвижный шарнир. Точка крепления перемещаться не может.

Стержень может свободно поворачиваться вокруг оси шарнира. Реакция такой опоры проходит через ось шарнира, но неизвестна по направлению. Ее изображают в виде двух составляющих: горизонтальной и вертикальной (R_x, R_y).

Защемление, или «заделка». Любые перемещения точки крепления невозможны.

Под действием внешних сил в опоре возникают реактивная сила и реактивный момент М_z, препятствующий повороту.

Реактивная сила представляется в виде двух составляющих вдоль осей координат:

3. Определение равнодействующей геометрическим способом

Система сил, линии действия которых пересекаются в одной точке, называется сходящейся.

Необходимо определить равнодействующую системы сходящихся сил (F₁; F₂; F₃;…; F_n), где n – число сил, входящих в систему.

В соответствии со следствиями из аксиом статики, все силы системы можно переместить вдоль линии действия, и все силы окажутся приложенными к одной точке.

Используя свойство векторной суммы сил, можно получить равнодействующую любой сходящейся системы сил, складывая последовательно силы, входящие в систему. Образуется многоугольник сил.

При графическом способе определения равнодействующей векторы сил можно вычерчивать в любом порядке, результат (величина и направление равнодействующей) при этом не изменится.

Вектор равнодействующей направлен навстречу векторам сил-слагаемых. Такой способ получения равнодействующей называется геометрическим.

Многоугольник сил строится в следующем порядке.

1. Вычертить векторы сил заданной системы в некотором масштабе один за другим так, чтобы конец предыдущего вектора совпал с началом последующего.

2. Вектор равнодействующей замыкает полученную ломаную линию; он соединяет начало первого вектора с концом последнего и направлен ему навстречу.

3. При изменении порядка вычерчивания векторов в многоугольнике меняется вид фигуры. На результат порядок вычерчивания не влияет.

Условие равновесия плоской системы сходящихся сил. При равновесии системы сил равнодействующая должна быть равна нулю, следовательно, при геометрическом построении конец последнего вектора должен совпасть с началом первого.

Если плоская система сходящихся сил находится в равновесии, многоугольник сил этой системы должен быть замкнут.

Если в системе три силы, образуется треугольник сил.

Геометрическим способом пользуются, если в системе три силы. При решении задач на равновесие тело считается абсолютно твердым (отвердевшим).

Задачи решаются в следующем порядке.

1. Определить возможное направление реакций связей.

2. Вычертить многоугольник сил системы, начиная с известных сил, в некотором масштабе. (Многоугольник должен быть замкнут, все векторы-слагаемые направлены в одну сторону по обходу контура).

3. Измерить полученные векторы сил и определить их величину, учитывая выбранный масштаб.

4. Для уточнения определить величины векторов (сторон многоугольника) с помощью геометрических зависимостей.

4. Определение равнодействующей аналитическим способом

Проекция сил на ось определяется отрезком оси, отсекаемой перпендикулярами, опущенными на ось из начала и конца вектора.

Величина проекции силы на ось равна произведению модуля силы на косинус угла между вектором силы и положительным направлением сил. Проекция имеет знак: положительный при одинаковом направлении вектора силы и оси и отрицательный при направлении в сторону отрицательной полуоси.

Проекция силы на две взаимно перпендикулярные оси.

Величина равнодействующей равна векторной (геометрической) сумме векторов системы сил. Определим равнодействующую аналитическим способом. Выберем систему координат, определим проекции всех заданных векторов на эти оси. Складываем проекции всех векторов на оси х и у.

Модуль (величину) равнодействующей можно определить по известным проекциям:

Направление вектора равнодействующей можно определить по величинам и знакам косинусов углов, образуемых равнодействующими с осями координат:

Плоская система сходящихся сил находится в равновесии, если алгебраическая сумма проекций всех сил системы на любую ось равна нулю.

Система уравнений равновесия плоской системы сходящихся сил:

При решении задач координатные оси выбирают так, чтобы решение было наиболее простым. При этом желательно, чтобы хотя бы одна неизвестная сила совпадала с осью координат.

5. Пара сил. Момент силы

Парой сил называется система двух сил, равных по модулю, параллельных и направленных в разные стороны.

Пара сил вызывает вращение тела, и ее действие на тело оценивается моментом. Силы, входящие в пару, не уравновешиваются, так как они приложены к двум точкам.

Действие этих сил на тело не может быть заменено одной равнодействующей силой.

Момент пары сил численно равен произведению модуля силы на расстояние между линиями действия сил плеча пары.

Источник