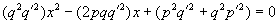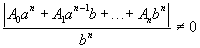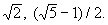что такое алгебраическое число

АЛГЕБРАИЧЕСКОЕ ЧИСЛО

Ч комплексное (в частности, действительное) число, являющееся корнем многочлена

с рациональными коэффициентами, из к-рых не все равны нулю. Если Ч А. ч., то среди всех многочленов с рациональными коэффициентами, имеющих своим корнем, существует единственный многочлен наименьшей степени со старшим коэффициентом, равным 1, и, следовательно, неприводимый (см. Неприводимый многочлен). Он наз. каноническим, или минимальным, многочленом А. ч.. Степень пканонич. многочлена наз. степенью А. ч.. Существование неприводимых многочленов любой степени побусловливает существование А. ч. степени п. Все рациональные числа, и только они, являются А. ч. 1-й степени. Число г есть А. ч. 2-й степени как корень многочлена при любом натуральном песть А. ч. степени пкак корень неприводимого многочлена .

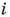
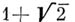
А. ч. наз. целым, если все коэффициенты в его канонич. многочлене Ч целые рациональные числа. Напр., и Ч целые А. ч. как корни многочленов и .

Понятие целого А. ч. является обобщением понятия целого рационального числа (целое рациональное число есть целое А. ч. как корень многочлена ). Многие свойства целых рациональных чисел сохраняются и для целых А. ч. Так, целые А. ч. образуют кольцо. Однако действительные целые А. ч. образуют всюду плотное множество, в то время как целые рациональные Ч дискретное множество. В 1872 Г. Кантор (G. Kantor) доказал, что множество всех А. ч. счетно, откуда следовало существование трансцендентных чисел.

Корень любого (не обязательно неприводимого) многочлена с целыми рациональными коэффициентами и старшим коэффициентом, равным единице, является целым А. ч. Более того, корень многочлена с целыми алгебраич. коэффициентами и старшим коэффициентом 1 есть целое А. ч. В частности, корень любой степени киз целого А. ч. есть целое А. ч. Для всякого А. ч. существует такое натуральное , что Ч целое А. ч. (аналогия с рациональными числами). В качестве наименьшего возможного числа можно взять модуль старшего коэффициента в неприводимом и примитивном многочлене с целыми рациональными коэффициентами, имеющем своим корнем. Все сопряженные целого А. ч.

Полезное

Смотреть что такое «АЛГЕБРАИЧЕСКОЕ ЧИСЛО» в других словарях:

АЛГЕБРАИЧЕСКОЕ ЧИСЛО — число, удовлетворяющее алгебраическому уравнению с целыми коэффициентами … Большой Энциклопедический словарь

алгебраическое число — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN polinomial number … Справочник технического переводчика

алгебраическое число — число, удовлетворяющее алгебраическому уравнению с целыми коэффициентами. * * * АЛГЕБРАИЧЕСКОЕ ЧИСЛО АЛГЕБРАИЧЕСКОЕ ЧИСЛО, число, удовлетворяющее алгебраическому уравнению с целыми коэффициентами … Энциклопедический словарь

АЛГЕБРАИЧЕСКОЕ ЧИСЛО — число, удовлетворяющее алгебр. ур нию с целыми коэффициентами … Естествознание. Энциклопедический словарь

Целое алгебраическое число — Целыми алгебраическими числами называются комплексные (и в частности вещественные) корни многочленов с целыми коэффициентами и со старшим коэффициентом, равным единице. По отношению к сложению и умножению комплексных чисел, целые алгебраические… … Википедия

Число (матем.) — Число, важнейшее математическое понятие. Возникнув в простейшем виде ещё в первобытном обществе, понятие Ч. изменялось на протяжении веков, постепенно обогащаясь содержанием по мере расширения сферы человеческой деятельности и связанного с ним… … Большая советская энциклопедия

Источник

Алгебраические числа

Первоначальные элементы математики связаны с появлением навыков счета, возникающих в примитивной форме на сравнительно ранних ступенях развития человеческого общества, в процессе трудовой деятельности.

Исторически теория чисел возникла как непосредственное развитие арифметики. В настоящее время в теорию чисел включают значительно более широкий круг вопросов, выходящих за рамки изучения натуральных чисел. В теории чисел рассматриваются не только натуральные числа, но и множество всех целых чисел, а так же множество рациональных чисел.

Если рассматривать корни многочленов: f(x)=x n +a 1 x n-1 +…+a n с целыми коэффициентами, то обычные целые числа соответствуют случаю, когда этот многочлен имеет степень n=1. Во множестве комплексных чисел естественно выделить так называемые целые алгебраические числа, представляющие собой корни многочленов с целыми коэффициентами.

Изучение свойств таких чисел составляет содержание одного из важнейших разделов современной теории чисел, называемого алгебраической теорией чисел. Она связана с изучением различных классов алгебраических чисел.

I. Краткий исторический очерк.

Огромное значение в развитии теории чисел имели замечательные работы К. Гаусса (1777-1855). Гаусс наряду с изучением обычных чисел начал рассматривать так же и арифметику чисел, получивших название целых гауссовских чисел, а именно числа вида a+bi, где a и b – обычные целые числа. Эти его исследования положили начала алгебраической теории чисел.

Теория алгебраических чисел была построена в работах Куммера (1810-1893) и Дирихле (1805-1859) и развита затем Кронекером (1823-1891), Дедекиндом (1831-1916) и Е.И. Золотаревым (1847-1878). Работы Лиувилля (1809-1882) и Эрмита (1822-1901) явились основой трансцендентных чисел.

Вопросы аппроксимации алгебраических чисел рациональными были существенно продвинуты в начале века А. Туэ, а затем в пятидесятых годах в работах К. Рота.

В последнее время все большее внимание специалистов по теории чисел привлекает алгебраическая теория чисел.

Здесь надо назвать работы Г. Хассе, Е. Гекке, а в особенности французского математика А. Вейля, результаты которого были использованы во многих теорико-числовых исследованиях, как например Д. Берджессом в проблеме о наименьшем квадратичном вычете.

К алгебраической теории чисел относятся и интересные работы советского математика И.Р. Шафаревича, а так же работы Б.Н. Делонга по теории кубических форм.

II. Поле алгебраических чисел.

2.1 Понятие числового поля

Естественный и важный подход к выделению и изучению тех или иных множеств чисел связан с замкнутостью множеств чисел относительно тех или иных действий.

В отношении умножения множество N так же замкнуто. Но оно не является замкнутым относительно вычитания и деления. Действительно:

5, 7 О N, но 5-7=-2 П N,

3, 2О N, но 3:2=1,5 П N

В связи с замкнутостью действий на множестве выделились классы числовых множеств.

Рассмотрим один их классов, называемых полем.

Последнее означает, что для любых a, b О M, должно иметь место a+b, a-b, a*b О M. Так же для любого aО M и любого b№ 0 из М, должно выполняться a:bО M.

Среди важнейших числовых полей наиболее важными являются:

Что касается множества всех целых чисел, то оно не является числовым полем, ибо не замкнуто относительно деления.

Существует бесконечно много числовых полей. Нас, в данном случае интересует поле алгебраических чисел.

2. 2 Определение алгебраического числа.

Существуют различные признаки, по которым их общего множества Z выделяю те или иные подмножества, подвергаемые специальному изучению. С точки зрения важного для алгебры понятия алгебраического уравнения, естественным представляется выделение классов чисел, являющихся корнями алгебраических уравнений, коэффициенты которых принадлежат тому или иному классу чисел.

a n x n +a n-1 x n-1 +…+a 1 x+a 0 =0

a n z n +a n-1 z n-1 +…+a 1 z+a 0 =0

Числа не являющиеся алгебраическими называются трансцендентными.

К алгебраическим числам принадлежат, в частности, и все рациональные числа. Действительно, рациональное число z= 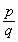(p, qО N) очевидно является корнем уравнения: qx-p=0.

Также всякое значение корня любой степени из рационального числа является алгебраическим числом. Действительно, число z= 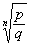(p, qО N) является корнем уравнения:

Существуют и другие алгебраические числа, нежели указанное выше.

, (p, q, О N).

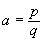
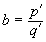
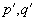
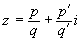
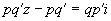
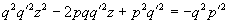
Из равенства , получаем: . Отсюда, возводя в квадрат, получим: . Следовательно, z является корнем уравнения:

все коэффициенты которого целые числа.

В дальнейшем мы будем рассматривать только действительные алгебраические числа, не оговаривая этого каждый раз.

Из f(x)=0 следует f(z)j (x)=0, где в качестве j (x) можно взять любой многочлен с целыми коэффициентами. Таким образом для любого алгебраического числа z, из всех этих многочленов обычно рассматривают многочлен наименьшей степени.

Определение 4: Число n называется степенью алгебраического числа z, если z есть корень некоторого многочлена n-ой степени с рациональными коэффициентами и не существует тождественно не равного нулю многочлена с рациональными коэффициентами степени, меньшей чем n, корнем которого является z.

Если корень многочлена n-ой степени с целыми рациональными коэффициентами z не является корнем ни одного тождественно неравного нулю многочлена с целыми коэффициентами степени меньшей чем n, то z не может быть корнем и тождественно неравного нулю многочлена с рациональными коэффициентами степени меньшей чем n, т.е. z – алгебраическое число степени n.

Рациональные числа являются алгебраическими числами первой степени. Любая квадратическая иррациональность представляет собой алгебраическое число 2-й степени, так как, являясь корнем квадратичного уравнения с целыми коэффициентами, она не является корнем какого-либо уравнения 1-й степени с целыми коэффициентами. Алгебраические числа 3-й степени часто называют кубическими иррациональностями, а 4-й степени биквадратическими иррациональностями.

не является корнем какого-либо многочлена 1-й или 2-й степени с целыми коэффициентами.

Определение 5 : Если алгебраическое число n-й степени z является корнем многочлена f(x)=x n +b 1 x n-1 + … +b n (nі 1) (1) с рациональными коэффициентами, то f(x) называется минимальным многочленом для z.

Таким образом, минимальным многочленом для z называется многочлен наименьшей степени с рациональными коэффициентами и старшим коэффициентом, равном единице, корнем которого является z.

Если вместо многочлена (1) взять какой-либо другой многочлен с рациональными коэффициентами степени n, корнем которого является z, то многочлен (1) может быть получен из него делением всех коэффициентов на старший член.

не является корнем какого-либо многочлена степени с рациональными коэффициентами.

Теорема 1: Если f(x) минимальный многочлен алгебраического числа z и f(x) многочлен с рациональными коэффициентами, такой, что F(z)=0, то f(x) делитель F(x), т.е. F(x)=f(x)g(x), где g(x) также многочлен с рациональными коэффициентами.

Доказательство: Согласно известной теореме алгебры F(x) можно представить в виде:

где g(x) и r(x) – многочлены с рациональными коэффициентами, причем степень r(x) меньше степени f(x). Поскольку F(x)=0 и f(z)=0, то придавая x значение z, получаем r(z)=0; z – корень многочлена r(x) с рациональными коэффициентами степени, меньшей чем у минимального для z многочлена, т.е. меньшей чем степень z. Это может быть только если r(x) тождественно равен нулю, а значит F(x)=f(x)g(x). Теорема доказана.

Теорема 2: Для любого алгебраического числа z минимальный многочлен неприводим над полем рациональных чисел.

Пусть f(x) – минимальный многочлен для z. Предположим, что f(x) приводим над полем рациональных чисел, т.е., что f(x)=w (x)j (x), w (x)j (x) – многочлены с рациональными коэффициентами, степени меньшей, чем n.

Из равенства w (x)j (x)=f(x)=0 следует, что из двух чисел w (x) и j (x), по крайней мере одно равно нулю. Пусть например w (x)=0, тогда z – корень тождественно не равного нулю многочлена w (x) с рациональными коэффициентами, степени меньшей, чем n, т.е. меньшей чем у f(x). А это противоречит тому, что f(x) – минимальный многочлен для z. Предположение, что f(x) приводим над полем рациональных чисел, оказалось неверным, т.е. f(x) неприводим над этим полем. Теорема доказана.

Теорема 3: Если z корень неприводимого над полем рациональных чисел многочлена F(x) с рациональными коэффициентами степени n, то z – алгебраическое число степени n.

Обозначим минимальный многочлен для z через f(x). Согласно теоремы 1: F(x)=f(x)g(x); где g(x) – многочлен с рациональными коэффициентами. Поскольку F(x) неприводим над полем рациональных чисел и f(x) отлично от постоянного, то g(x)=c, где c – рационально. F(x)=cf(x), т.е. z – алгебраическое число n-й степени. Теорема доказана.

Пусть p – простое число.

при любом простом целом a (a>1), не равном p-ой степени другого целого, представляет собой алгебраическое число степени p. Действительно это число есть корень неприводимого над полем рациональных чисел многочлена.

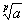
2.3. Поле алгебраических чисел

Теорема 4: Множество всех действительных алгебраических чисел представляет собой поле, т.е. сумма, разность, произведение и частное двух алгебраических чисел a и b (для частного при b№ 0) являются алгебраическими числами.

F(x)=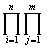(x-(a i +b i ))=

F(x)=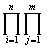(x-a ib i ) (3)

Разность может быть представлена в виде a +(-b ), т.е. в виде суммы двух алгебраических чисел. При b№ 0 частное 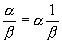, являясь произведением двух алгебраических чисел, представляет собой так же алгебраическое число.

Из теоремы единственности над полем рациональных чисел множители f(x) должны являться произведением каких-то множителей правой части равенства (4). Легко видеть, что из этих множителей нельзя составить многочлен с рациональными коэффициентами степени меньшей, чем 4, т.е. f(x) – неприводимый над полем рациональных чисел многочлен, а, следовательно, согласно теореме 3, 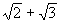— алгебраическое число 4-й степени.

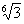
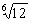
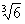
2) a = и b =, как легко видеть, это алгебраические числа 6-й степени, а произведение ab = — алгебраическое число 3-й степени.

III. Рациональные приближения

3.1. Теорема Лиувилля.

Алгебраические числа не могут иметь слишком хороших рациональных приближений: погрешность при замене алгебраического числа рациональной дробью не может быть достаточно мала по порядку в сравнении с величиной, обратной знаменателю рациональной дроби.

(5)

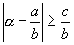
Для алгебраического числа 2-й степени можно подобрать c>0, такое, что для любой рациональной дроби, будет иметь место неравенство:

(6)

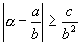
В 1844 г., французским математиком Лиувиллем, впервые была доказана общая теорема:

(7)

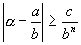
Согласно теореме Безу, имеем:

где g(x) – многочлен с действительными коэффициентами.

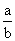
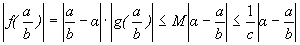
Для произвольного рационального числа могут представиться две возможности:

(9)

f()=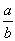

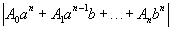
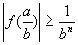
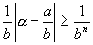
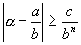
Поскольку числитель — целое неотрицательное, отличное от нуля, т.е. число большее или равное 1, то (10). Сравнивая неравенства (9) и (10) получаем , так что и в этом случае имеем: . Теорема доказана.

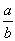
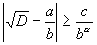
Пусть z – неквадратное целое число. Найти c >0, такое, что для всех рациональных чисел имело бы место неравенство:

.

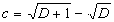
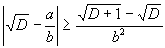
При таком d получаем , так что при любых целых a и b имеем: .

3.2. Трансцендентные числа Лиувилля.

Числа, являющиеся корнями уравнений с целыми коэффициентами, не исчерпывают все множество действительных чисел, т.е. существуют действительные числа отличные от алгебраических.

Впервые существование трансцендентных чисел доказано Лиувиллем. Доказательство существования трансцендентных чисел у Лаувилля эффективно; на основе следующей теоремы, являющейся непосредственным следствием теоремы 5, строятся конкретные примеры трансцендентных чисел.

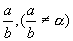
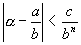
Теорема 6: Пусть a – действительное число. Если для любого натурального nі 1 и любого действительного c >0 существует хотя бы одна рациональная дробь , такая, что (11), то a – трансцендентное число.

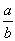
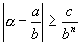
Если бы a было алгебраическим, то нашлось бы (теорема 5) целое положительное n и действительное c >0 такие, что для любой дроби было бы , а это противоречит тому, что имеет место (11). Предположение, что a алгебраическое число, т.е. трансцендентное число. Теорема доказана.

a – трансцендентное число.

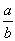
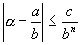
Поскольку для произвольных nі 1 и c >0 можно найти дробь такую, что , то a – трансцендентное число.

Алгебраические числа имеют широкое применение в теории чисел, алгебре, геометрии и других разделов математики. Они позволяют раскрыть вариантности алгебры для практических приложений. Это имеет большое значение в подготовке учителя для средней школы.

Изучение свойств таких чисел составляет содержание одного из важнейших разделов современной теории чисел, называемого алгебраической теорией чисел.

К этому разделу относятся вопросы, связанные с изучением различных классов алгебраических чисел.

Эта работа может служить в качестве учебного пособия при изучении теории алгебраических чисел. А так же она удобна в использовании при подготовке к экзамену.

В работе введена сплошная нумерация теорем и определений арабскими цифрами. Все теоремы даны с полными доказательствами. Приведенные примеры алгебраических чисел и действий над ними, даны с доступными пояснениями и, при необходимости, с доказательством.

Большое место в работе занимают теоретические сведения о развитии алгебры теории чисел. Помимо введения, дающего общий очерк развития теории чисел, первый параграф посвящен уже конкретно развитию теории алгебраических чисел. Так же на протяжении всей работы можно наблюдать исторические комментарии.

Данная работа дает представление о современном состоянии рассматриваемого вопроса и дает представление о теории алгебраических чисел и о теории чисел вообще, как о развивающейся науке.

Ошибка в тексте? Выдели её мышкой и нажми

Источник

Алгебраическое число

Полезное

Смотреть что такое «Алгебраическое число» в других словарях:

АЛГЕБРАИЧЕСКОЕ ЧИСЛО — число, удовлетворяющее алгебраическому уравнению с целыми коэффициентами … Большой Энциклопедический словарь

алгебраическое число — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN polinomial number … Справочник технического переводчика

алгебраическое число — число, удовлетворяющее алгебраическому уравнению с целыми коэффициентами. * * * АЛГЕБРАИЧЕСКОЕ ЧИСЛО АЛГЕБРАИЧЕСКОЕ ЧИСЛО, число, удовлетворяющее алгебраическому уравнению с целыми коэффициентами … Энциклопедический словарь

АЛГЕБРАИЧЕСКОЕ ЧИСЛО — число, удовлетворяющее алгебр. ур нию с целыми коэффициентами … Естествознание. Энциклопедический словарь

АЛГЕБРАИЧЕСКОЕ ЧИСЛО — Ч комплексное (в частности, действительное) число, являющееся корнем многочлена с рациональными коэффициентами, из к рых не все равны нулю. Если Ч А. ч., то среди всех многочленов с рациональными коэффициентами, имеющих своим корнем, существует… … Математическая энциклопедия

Целое алгебраическое число — Целыми алгебраическими числами называются комплексные (и в частности вещественные) корни многочленов с целыми коэффициентами и со старшим коэффициентом, равным единице. По отношению к сложению и умножению комплексных чисел, целые алгебраические… … Википедия

Число (матем.) — Число, важнейшее математическое понятие. Возникнув в простейшем виде ещё в первобытном обществе, понятие Ч. изменялось на протяжении веков, постепенно обогащаясь содержанием по мере расширения сферы человеческой деятельности и связанного с ним… … Большая советская энциклопедия

Источник