что такое алгоритмическая структура цикла
Алгоритмическая структура «Цикл»
В алгоритмическую структуру «цикл» входит серия команд, выполняемая многократно. Такая последовательность команд называется телом цикла.
Циклические алгоритмические структуры бывают двух типов:
• циклы со счетчиком, в которых тело цикла выполняется определенное количество раз;
• циклы с условием, в которых тело цикла выполняется, пока условие истинно или ложно.
Алгоритмическая структура «цикл» может быть зафиксирована различными способами:
• графически – с помощью блок-схемы;
• на языке программирования, например, на языке Паскаль с использованием специальных инструкций, реализующих циклы различного типа.
Цикл со счетчиком. Когда заранее известно, какое число повторений тела цикла необходимо выполнить, можно воспользоваться циклической инструкцией.
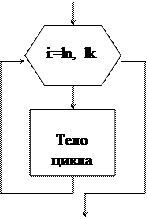
В начале выполнения цикла значение переменной i устанавливается равным In. При каждом проходе цикла переменная i увеличивается на величину шага. Если она достигает величины, большей Ik, то цикл завершается и выполняются следующие за ним операторы (нц – начало цикла, кц – конец цикла).

Циклы с условием. Часто бывает так, что необходимо повторить тело цикла, но заранее неизвестно, какое количество раз это надо сделать. В таких случаях количество повторений зависит от некоторого условия.
Условие выхода из цикла можно поставить в начале, перед телом цикла. Такой цикл называется циклом с предусловием.
цикл выполняется, пока условие имеет значение «истина». Как только условие примет значение «ложь», выполнение цикла закончится. В этом случае условие является условием продолжения цикла.
Условие выхода из цикла можно поставить в конце, после тела цикла. Такой цикл называется «циклом с постусловием». цикл выполняется, пока условие имеет значение «ложь». Как только условие примет значение «истина», выполнение цикла закончится. В этом случае условие является условием завершения «цикла».
Цикл с постусловием, в отличие от цикла с предусловием, выполняется обязательно как минимум один раз, независимо от того, выполняется условие или нет.


Примеры
Даны две простые дроби. Составить алгоритм получения дроби, являющейся результатом их деления.
В алгебраической форме решение задачи выглядит следующим образом:

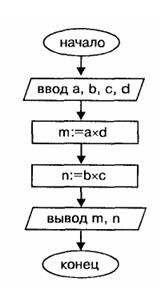
Исходными данными являются четыре целые величины: а, b, с, d. Результат – два целых числа m и n.

Тест: a = 3, b=4, c=5, d=6. Результат: m = 18, n = 20.
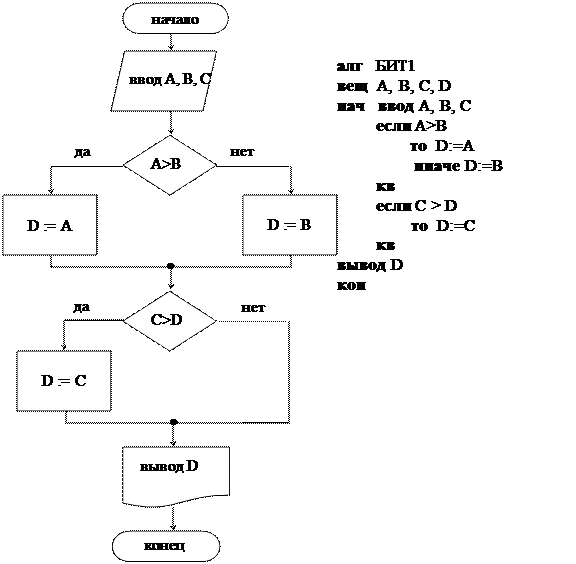
Даны три вещественных числа А, В, С. Найти наибольшее среди них.
Сначала определяется большее среди двух значений А и В, затем большее между найденным значением и величиной С. Алгоритм имеет структуру двух

Задача решается c помощью циклического алгоритма: цикла с параметром.
|
 |




 |  |
Тест: N = 5. Результат: факториал F = 120.
вычислить значение функции Y = A = BX + CX 2 для 
 |
Использование вложенных циклов на примере вычисления двойной суммы

А= 
В = (b1, b2, b3, …, bk) – одномерный массив (вектор) данных одного и того же типа.
 |
|
Замечание. В соответствии с ГОСТ 19.701-90 границы цикла можно изображать следующим образом:
Начало цикла и конец цикла – оба символа имеют один и тот же идентификатор. Условия инициализации, приращения, завершения и т.д. помещаются внутри графического символа в начале или в конце в зависимости от расположения операции, проверяющей условие.
Урок 19. Алгоритмическая структура «Цикл»
При решении задач может возникнуть необходимость повторить одни и те же действия несколько или множество раз. В программировании блоки кода, которые требуется повторять не единожды, оборачиваются в специальные конструкции – циклы. У циклов выделяют заголовок и тело. Заголовок определяет, до каких пор или сколько раз тело цикла будет выполняться. Тело содержит выражения, которые выполняются, если в заголовке цикла выражение вернуло логическую истину (True, не ноль). После того как достигнута последняя инструкция тела, поток выполнения снова возвращается к заголовку цикла. Снова проверяется условие выполнения цикла. В зависимости от результата тело цикла либо повторяется, либо поток выполнения переходит к следующему выражению после всего цикла.
В языке программирования Паскаль существует три вида циклических конструкций.
Часто цикл for называют циклом со счетчиком. Этот цикл используется, когда число повторений не связано с тем, что происходит в теле цикла. Т.е. количество повторений может быть вычислено заранее (хотя оно не вычисляется).
В заголовке цикла указываются два значения. Первое значение присваивается так называемой переменной-счетчику, от этого значения начинается отсчет количества итераций (повторений). Отсчет идет всегда с шагом равным единице. Второе значение указывает, при каком значении счетчика цикл должен остановиться. Другими словами, количество итераций цикла определяется разностью между вторым и первым значением плюс единица. В Pascal тело цикла не должно содержать выражений, изменяющих счетчик.
Цикл for существует в двух формах:
for счетчик:=значение to конечное_значение do тело_цикла;
for счетчик:=значение downto конечное_значение do тело_цикла;
Счетчик – это переменная любого из перечисляемых типов (целого, булевого, символьного, диапазонного, перечисления). Начальные и конечные значения могут быть представлены не только значениями, но и выражениями, возвращающими совместимые с типом счетчика типы данных. Если между начальным и конечным выражением указано служебное слово to, то на каждом шаге цикла значение параметра будет увеличиваться на единицу. Если же указано downto, то значение параметра будет уменьшаться на единицу.
Количество итераций цикла for известно именно до его выполнения, но не до выполнения всей программы. Так в примере ниже, количество выполнений цикла определяется пользователем. Значение присваивается переменной, а затем используется в заголовке цикла. Но когда оно используется, циклу уже точно известно, сколько раз надо выполниться.
var i, n: integer; begin write (‘Количество знаков: ‘); readln (n); for i := 1 to n do write (‘(*) ‘); readln end.
Цикл while является циклом с предусловием. В заголовке цикла находится логическое выражение. Если оно возвращает true, то тело цикла выполняется, если false – то нет.
Когда тело цикла было выполнено, то ход программы снова возвращается в заголовок цикла. Условие выполнения тела снова проверяется (находится значение логического выражения). Тело цикла выполнится столько раз, сколько раз логическое выражение вернет true. Поэтому очень важно в теле цикла предусмотреть изменение переменной, фигурирующей в заголовке цикла, таким образом, чтобы когда-нибудь обязательно наступала ситуация false. Иначе произойдет так называемое зацикливание, одна из самых неприятных ошибок в программировании.
var i, n: integer; begin write (‘Количество знаков: ‘); readln (n); i := 1; while i
Цикл while может не выполниться ни разу, если логическое выражение в заголовке сразу вернуло false. Однако такая ситуация не всегда может быть приемлемой. Бывает, что тело цикла должно выполниться хотя бы один раз, не зависимо оттого, что вернет логическое выражение. В таком случае используется цикл repeat – цикл с постусловием.
В цикле repeat логическое выражение стоит после тела цикла. Причем, в отличие от цикла while, здесь всё наоборот: в случае true происходит выход из цикла, в случае false – его повторение.
var i, n: integer; begin write (‘Количество знаков: ‘); readln (n); i := 1; repeat write (‘(*) ‘); i := i + 1 until i > n; readln end.
Алгоритмическая структура «Цикл»
В алгоритмическую структуру «цикл» входит серия команд, выполняемая многократно. Такая последовательность команд называется телом цикла.
Циклические алгоритмические структуры бывают двух типов:
• циклы со счетчиком, в которых тело цикла выполняется определенное количество раз;
• циклы с условием, в которых тело цикла выполняется, пока условие истинно или ложно.
Алгоритмическая структура «цикл» может быть зафиксирована различными способами:
• на языке программирования, например, на языке Паскаль с использованием специальных инструкций, реализующих циклы различного типа.
Цикл со счетчиком. Когда заранее известно, какое число повторений тела цикла необходимо выполнить, можно воспользоваться циклической инструкцией.
В начале выполнения цикла значение переменной i устанавливается равным In. При каждом проходе цикла переменная i увеличивается на величину шага. Если она достигает величины, большей Ik, то цикл завершается и выполняются следующие за ним операторы (нц – начало цикла, кц – конец цикла).
Циклы с условием. Часто бывает так, что необходимо повторить тело цикла, но заранее неизвестно, какое количество раз это надо сделать. В таких случаях количество повторений зависит от некоторого условия.
Условие выхода из цикла можно поставить в начале, перед телом цикла. Такой цикл называется циклом с предусловием.
цикл выполняется, пока условие имеет значение «истина». Как только условие примет значение «ложь», выполнение цикла закончится. В этом случае условие является условием продолжения цикла.
Условие выхода из цикла можно поставить в конце, после тела цикла. Такой цикл называется «циклом с постусловием». цикл выполняется, пока условие имеет значение «ложь». Как только условие примет значение «истина», выполнение цикла закончится. В этом случае условие является условием завершения «цикла».

Повторять
|
до тех пор, пока не выполнится
Примеры
Пример 1. Даны две простые дроби. Составить алгоритм получения дроби, являющейся результатом их деления.
Решение. В алгебраической форме решение задачи выглядит следующим образом:
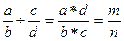
 | |
|
 |
 |
Тест: a = 3, b=4, c=5, d=6.
Результат: m = 18, n = 20.
Пример 2. Даны две переменные величины X и Y. Требуется произвести между ними обмен значениями. Обмен происходит через промежуточную переменную Z.
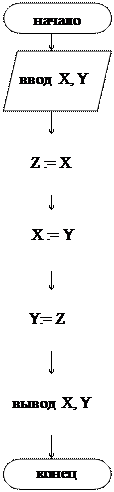


вывод X, Y
 |
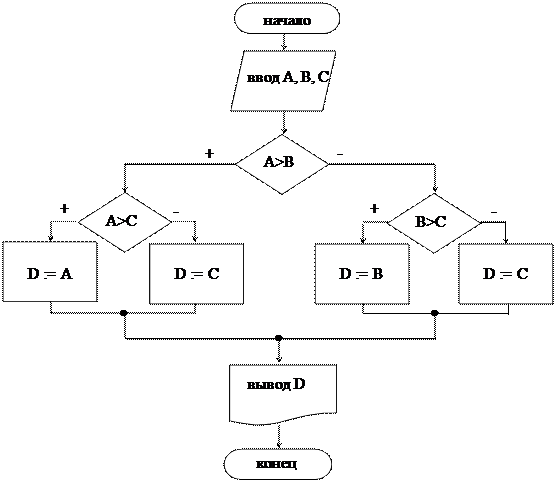
Пример 3. Даны три вещественных числа А, В, С. Найти наибольшее среди них.
Сначала определяется большее среди двух значений А и В, затем большее между найденным значением и величиной С. Алгоритм имеет структуру двух последовательных ветвлений.
2 способ. Задача решена с помощью вложенных ветвлений.
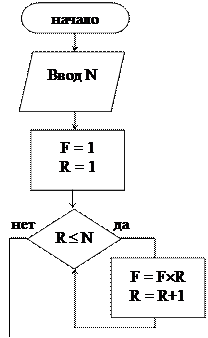
Решение. Задача решается c помощью циклического алгоритма. Составим два варианта алгоритма: цикла с параметром и с применением цикла с предусловием.
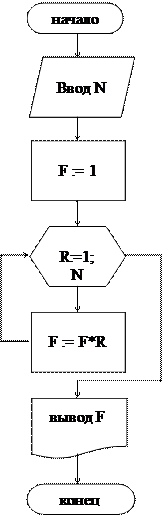 | |
|
Результат: факториал F = 120.
 | |
|

 |
Пример 5. вычислить значение функции Y = A = BX + CX 2 для 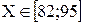
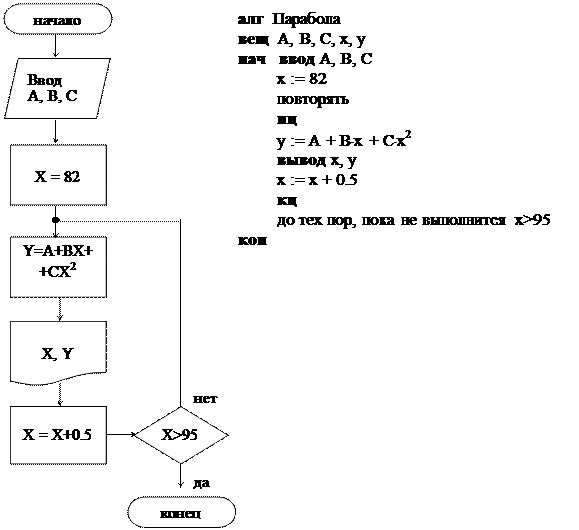 |
Пример 6. Вычислить выборочное среднее С и выборочную дисперсию D случайной величины x по формулам
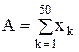
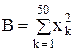
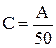
(х1, х2, …, х50 – выборочные значения случайной величины х).
Указание: при нахождении суммы (произведения) рекомендуется начальное значение суммы (произведения) брать равным нулю (единице) или первому слагаемому (множителю).
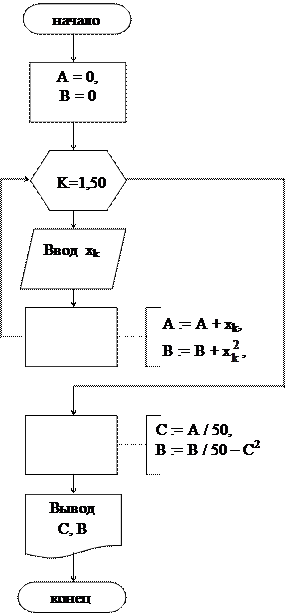 | |
|
Пример 7. Использование вложенных циклов на примере вычисления двойной суммы
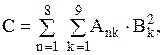
А= 
В = (b1, b2, b3, …, bk) – одномерный массив (вектор) данных одного и того же типа.
 |
|
Варианты
Задание по лабораторной работе «Алгоритмы в блок-схемах»
Составить алгоритмы на уровне блок-схем решения задач 5.1., 5.2., 5.3., 5.4., 5.5., 5.6. Контроль решения задачи или тест или ожидаемый результат должен быть рассмотрен и подготовлен до решения задачи с помощью ЭВМ. Номер варианта указывает преподаватель.
Задачи на линейный алгоритм
5.1.1. Вычислить объем конуса и площадь основания. Даны радиус основания R и высота конуса H. (V= 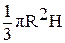
5.1.2. Вычислить радиус вписанного в треугольник круга по сторонам треугольника.
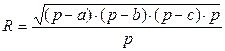
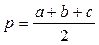
5.1.3. Даны два числа. Найти их сумму, произведение и разность.
5.1.4. Дано t. Камень бросили в колодец, и через t секунд послышался всплеск воды. На какой глубине (от сруба) вода в колодце. (h= g*t 2 /2)
5.1.5.Составить программу вычисления площади треугольника по его трем углам A, B, C и стороне a.
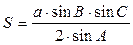
5.1.6.Вычислить площадь поверхности цилиндра по радиусу основания R и высоте цилиндра H. 
5.1.7.Дана сторона куба. Вычислить объем куба и полную поверхность.
5.1.8.Даны площадь треугольника S и стороны a, b, c. Вычислить сумму его высот.
5.1.9.Вычислить радиус описанного круга по сторонам треугольника.


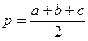
5.1.10.Вычислить площадь трапеции по ее основаниям и высоте. 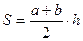
5.1.11.Длины сторон первого прямоугольника a и b, его площадь в 6 раз меньше площади второго прямоугольника. Найти длину стороны второго прямоугольника, если длина одной из его сторон равна c.
5.1.13.Длина стороны треугольника равна a, периметр равен Р, длины двух других сторон равны между собой. Найти эти длины.
5.1.15.Найти полную поверхность конуса с высотой H и радиусом основания R 
Задачи на разветвление
5.2.1. Написать алгоритм нахождения максимального среди четырех целых чисел.
5.2.2. Написать алгоритм проверки условия: имеются ли среди трех целых чисел два положительных числа?
5.2.3. Написать алгоритм проверки условия: могут ли три данных числа быть длинами сторон треугольника?
5.2.4. Написать алгоритм проверки условия: лежит ли данная точка c координатами (х, у) в первой четверти координатной плоскости?
5.2.5. Проверить принадлежность числа x интервалам [а,b] или [c,d].
5.2.6. Проверить, является ли четырехугольник со сторонам a, b, c, d ромбом.
5.2.7. Определить, является ли треугольник со сторонами а, b, c равнобедренным.
5.2.8. Определить, является ли треугольник со сторонами а, b, c равносторонним.
5.2.9. Среди чисел а, b, с определить количество отрицательных.
5.2.10. Среди чисел а, b, с определить количество положительных.
5.2.12. Определить, принадлежит ли заданная точка (х,у) плоской фигуре, являющейся кольцом с центром в начале координат, с внутренним радиусом r1 и внешним радиусом r2.
5.2.14. Выбрать среди данных четырех чисел a, b, c, d те, которые принадлежат интервалу (m, n).
5.2.15. Сколько чисел среди а, b, c, d принадлежит отрезку [m, n].



 кц кц выводС кон
кц кц выводС кон


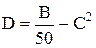
 кц C:= A/50 B:=B/50 – C 2 вывод “значение С=”, С “значение В=”, В кон
кц C:= A/50 B:=B/50 – C 2 вывод “значение С=”, С “значение В=”, В кон кц кц выводС кон
кц кц выводС кон