что такое arg в математике
Что такое arg в математике
VII .1. Формы записи комплексных чисел и действия над ними
где x и y – действительные числа, а i так называемая мнимая единица. Соотношение для мнимой единицы
Понятия «больше» и «меньше» для комплексных чисел не вводятся.
Числа z = x + iy и 
Алгебраической формой комплексного числа называется з апись числа z в виде z = x + iy.
Модуль r и аргумент φ можно рассматривать как полярные координаты вектора 
Равенство (7.3) есть тригонометрическая форма комплексного числа. Модуль r = |z| однозначно определяется по формуле
Аргумент определяется из формул:
Используя формулу Эйлера
комплексное число 
где r =| z | — модуль комплексного числа, а угол 
Пример 7.1. Записать комплексные числа 
На множестве комплексны х чисел определен ряд операций.
Из (7.11) следует важнейшее соотношение i 2 = –1. Действительно,
Видно, что при умножении комплексных чисел в тригонометрической форме их модули перемножаются, а аргументы складываются. Это правило распространяется на любое конечное число множителей. Нетрудно видеть, что если есть n множителей и все они одинаковые, то частным случаем равенства (7.12) является формула возведения комплексного числа в натуральную степень:
(7.13) называется первой формулой Муавра.
Произведение двух комплексных чисел в показательной (экспоненциальной) форме имеет вид:
На практике при нахождении частного двух комплексных чисел удобно умножить числитель и знаменатель дроби 
Деление комплексных чисел осуществляется также и в тригонометрической форме, при этом имеет место формула:
Видно, что при делении комплексных чисел их модули делятся, а аргументы вычитаются соответственно.
Частное двух комплексных чисел в показательной (экспоненциальной) форме имеет вид:
Пользуясь формулой (7.11), вычислим их произведение
На основании формулы (7.14) вычислим их частное
Решение. Используя (7.4) и (7.5), получаем:
Аналогично, для z 2 можно записать:
По формулам (7.12) и (7.16) получим в тригонометрической форме:
Пользуясь формулами (7.14) и (7.17), получим в показательной форме:
в натуральную степень, определенному ранее формулой (7.13).
(7.18) называется второй формулой Муавра.
Пример 7.4. Найти все корни уравнения z 4 +16=0.
Теорема 7.1 (основная теорема алгебры). Для всякого многочлена с комплексными коэффициентами
Приведем еще одну теорему, имеющую место над множеством комплексных чисел.
Таким образом, произведение линейных множителей, соответствующих сопряженным корням, можно заменить квадратным трехчленом с действительными коэффициентами, а соответствующее квадратное уравнение будет иметь отрицательный дискриминант.
Учебник. Понятие комплексного числа
Комплексным числом называется выражение вида a + ib, где a и b – любые действительные числа, i – специальное число, которое называется мнимой единицей. Для таких выражений понятия равенства и операции сложения и умножения вводятся следующим образом:
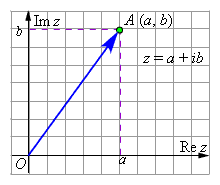
Комплексные числа часто обозначают одной буквой, например, z = a + ib. Действительное число a называется действительной частью комплексного числа z, действительная часть обозначается a = Re z. Действительное число b называется мнимой частью комплексного числа z, мнимая часть обозначается b = Im z. Такие названия выбраны в связи со следующими особыми свойствами комплексных чисел.
Мы хорошо помним, что геометрической интерпретацией действительных чисел является действительная прямая. Кроме того, как было установлено выше, на действительной прямой «нет места для новых точек», то есть любой точке на действительной оси отвечает действительное число. Следовательно, комплексные числа на этой прямой расположить уже нельзя, однако можно попытаться рассмотреть наряду с действительной осью, на которой мы будем откладывать действительную часть комплексного числа, ещё одну ось, ей перпендикулярную; будем называть её мнимой осью. Тогда любому комплексному числу z = x + iy можно поставить в соответствие точку координатной плоскости. На оси абсцисс будем откладывать действительную часть комплексного числа, а на оси ординат – мнимую часть. Таким образом мы построим взаимнооднозначное соответствие между всеми комплексными числами и всеми точками плоскости. Если такое соответствие построено, то координатная плоскость называется комплексной плоскостью.
Рассмотренные интерпретации комплексного числа позволяют называть комплексное число вектором или точкой на комплексной плоскости.
Комплексные числа на плоскости
Модулем комплексного числа называется длина вектора, соответствующего этому числу:
Модуль комплексного числа z обычно обозначается | z | или r. Указанная в определении формула легко выводится при помощи теоремы Пифагора (см. рис.).
Аргументом комплексного числа z = a + ib (z ≠ 0) называется величина угла между положительным направлением действительной оси и вектором z → ; величина угла считается положительной, если угол отсчитывается против часовой стрелки, и отрицательным в противном случае.
Угол φ, аргумент комплексного числа, обозначается φ = arg z. Для числа z = 0 аргумент не определён.
Заданием только лишь своего модуля определяется только комплексное число z = 0.
Найти модуль и аргумент комплексного числа z = –1 – i.
Как легко понять знаки Σ и П с помощью программирования
Для тех, кто подзабыл матешу
Вот говорят, что если ты не закончил Физтех, ФПМ или Бауманку, тебе в программировании делать нечего. Почему так говорят? Потому что, дескать, ты не учил сложную математику, а в программировании без неё никуда.
Это всё чушь, конечно. Если вы плохо знаете математику, вы можете быть блестящим разработчиком. Вы вряд ли напишете драйверы для видеокарты, но вы запросто сделаете мобильное приложение или веб-сервис. А это — основные деньги в этой среде.
Но всё же, чтобы получить некоторое интеллектуальное превосходство, вот вам пара примеров из страшного мира математики. Пусть они покажут вам, что не все закорючки в математике — это ад и ужас. Вот две нестрашные закорючки.
Знак Σ — сумма
Когда математикам нужно сложить несколько чисел подряд, они иногда пишут так:
Σ (читается «сигма») — это знак алгебраической суммы, который означает, что нам нужно сложить все числа от нижнего до верхнего, а перед этим сделать с ними то, что написано после знака Σ.
На картинке выше написано следующее: «посчитать сумму всех чисел от 5 до 15, умноженных на два». То есть:
Давайте для закрепления ещё один пример. На картинке ниже будет сказано «Найди сумму квадратов чисел от 5 до 10». То есть «возьми все числа от 5 до 10, каждое из них возведи в квадрат, а результаты сложи».
Но мы с вами как программисты видим, что здесь есть повторяющиеся действия: мы много раз складываем числа, которые меняются по одному и тому же правилу. А раз мы знаем это правило и знаем, сколько раз надо его применить, то это легко превратить в цикл. Для наглядности мы показали, какие параметры в Σ за что отвечают в цикле:
Произведение П
С произведением в математике работает точно такое же правило, только мы не складываем все элементы, а перемножаем их друг на друга:
А если это перевести в цикл, то алгоритм получится почти такой же, что и в сложении:
Что дальше
Сумма и произведение — простые математические операции, пусть они и обозначаются страшными символами. Впереди нас ждут интегралы, дифференциалы, приращения и бесконечные ряды. С ними тоже всё не так сложно, как кажется на первый взгляд.
Функция ARG
Указывает аргумент о том, что вызываемая ячейка может передаваться на настраиваемую функцию, а также значение по умолчанию, возвращаемого настраиваемой функцией, если вызываемая ячейка не передает значение аргумента. Возвращает значение, указанное ячейкой вызова и параметром argName.
Синтаксис
ARG(argName _,[ _ defaultValue ])
Параметры
| Имя | Необходимость | Тип данных | Описание |
|---|---|---|---|
| argName | Обязательный | String | Имя аргумента о том, что вызываемая ячейка может передаваться в функцию. |
| Значение по умолчанию | Необязательный | Числовой | Значение, возвращаемого ARG, если вызываемая ячейка не прошла в значении для параметра argName. |
Комментарии
Как разработчик формы можно создать настраиваемые функции, разместив выражение в одной ячейке и назвав это выражение из одной или более других ячеек. Выражение может включать буквальные строки, функции ShapeSheet и ссылки на ячейки. Выражение также может включать определенные аргументы, которые передаются в вызываемой ячейке.
Ячейка вызова указывает ячейку, которая содержит настраиваемую функцию, а также любые аргументы, которые она хочет передать функции. Ячейка выражения оценивается, а результат возвращается в вызываемую ячейку.
Пример
В следующем примере показано, как использовать функцию ARG совместно с функцией EVALCELL для поиска среднего значения из набора из трех значений.
В ячейке выражения поместите следующий код, определяемый настраиваемой функцией:
В ячейках вызова поместите следующий код, который вызывает настраиваемую функцию:
Что такое *args и **kwargs в Python?
Функции — это жизнь. Правда? Если вы только начали осваивать Python, неважно — первый ли это ваш язык программирования, или вы пришли в Python из другого языка, то вы уже знаете о том, что количество параметров в объявлении функции соответствует количеству аргументов, которые передают функции при вызове.
Не позволяйте всяким значкам загонять себя в ступор. Тут нет ничего архисложного. В общем-то, если эти конструкции вам незнакомы — предлагаю с ними разобраться.
Позиционные и именованные аргументы
Сначала поговорим о том, чем они отличаются. В простейшей функции мы просто сопоставляем позиции аргументов и параметров. Аргумент №1 соответствует параметру №1, аргумент №2 — параметру №2 и так далее.
Для вызова функции необходимы все три аргумента. Если пропустить хотя бы один из них — будет выдано сообщение об ошибке.
Если при объявлении функции назначить параметру значение по умолчанию — указывать соответствующий аргумент при вызове функции уже необязательно. Параметр становится опциональным.
Опциональные параметры, кроме того, можно задавать при вызове функции, используя их имена.
В следующем примере установим три параметра в значение по умолчанию None и взглянем на то, как их можно назначать, используя их имена и не обращая внимания на порядок следования аргументов, применяемых при вызове функции.
Оператор «звёздочка»
Оператор * чаще всего ассоциируется у людей с операцией умножения, но в Python он имеет и другой смысл.
Этот оператор позволяет «распаковывать» объекты, внутри которых хранятся некие элементы. Вот пример:
Как пользоваться *args и **kwargs
Итак, мы знаем о том, что оператор «звёздочка» в Python способен «вытаскивать» из объектов составляющие их элементы. Знаем мы и о том, что существует два вида параметров функций. Вполне возможно, что вы уже додумались до этого сами, но я, на всякий случай, скажу об этом. А именно, *args — это сокращение от «arguments» (аргументы), а **kwargs — сокращение от «keyword arguments» (именованные аргументы).
Каждая из этих конструкций используется для распаковки аргументов соответствующего типа, позволяя вызывать функции со списком аргументов переменной длины. Например — создадим функцию, которая умеет выводить результаты, набранные учеником в тесте:
Итоги
Вот несколько советов, которые помогут вам избежать распространённых проблем, возникающих при работе с функциями, и расширить свои знания: