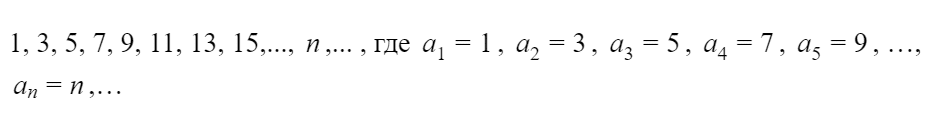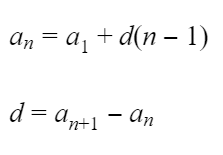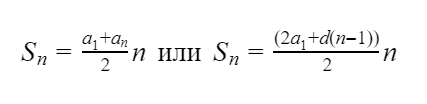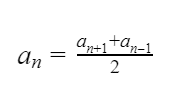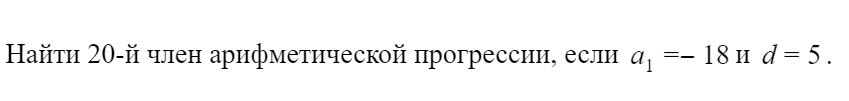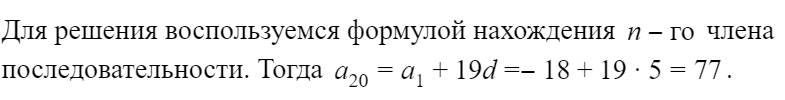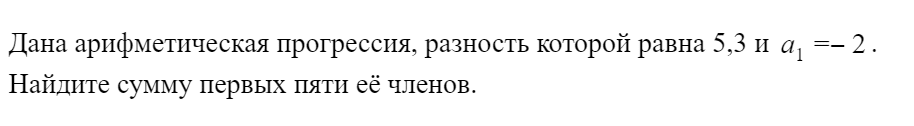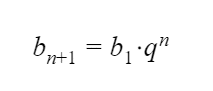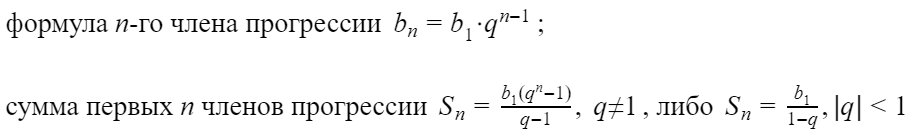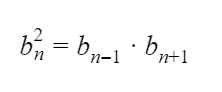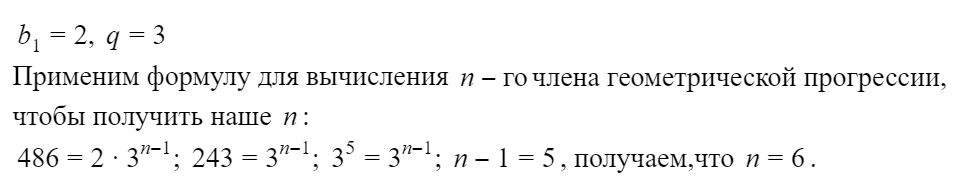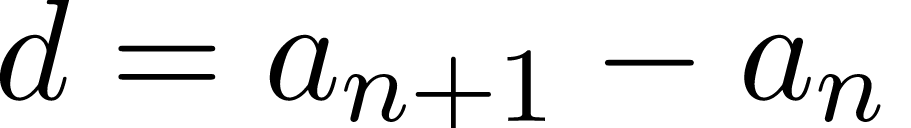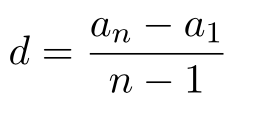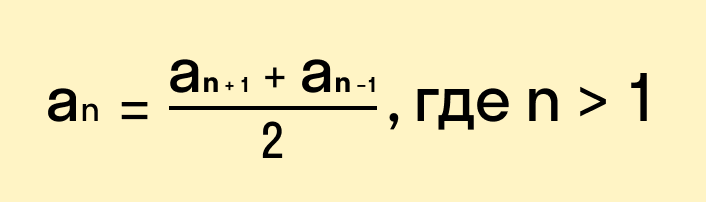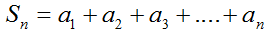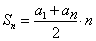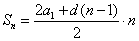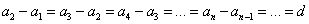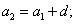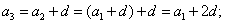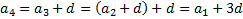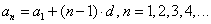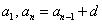что такое арифметическая прогрессия геометрическая прогрессия

Алгебра. Урок 6. Прогрессии

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

Числовые последовательности

Числовая последовательность – это функция, заданная на множестве натуральных чисел. Каждый элемент последовательности имеет свой порядковый номер.

Числа в последовательности могут быть любыми – положительными и отрицательными, целыми и дробными, рациональными и иррациональными.

Так почему же, спросите вы, в определении числовой последовательности есть фраза «функция, заданная на множестве натуральных чисел»? Потому что каждый член последовательности имеет свой порядковый номер (ну а нумеруем мы с единицы).

a 1 = 1, a 2 = 2, a 3 = 3, a 4 = 4, a 5 = 5, …

a 1 = 1, a 2 = 4, a 3 = 9, a 4 = 16, a 5 = 25, …

a 1 = − 3, a 2 = − 2, a 3 = − 1, a 4 = 0, a 5 = 1, a 6 = 2, a 7 = 3.

Числовые последовательности можно задавать несколькими способами:

Для нахождения каждого следующего члена последовательности требуется знать предыдущий.

n = 1, a n + 1 = a n + 1 ⇒ a 2 = a 1 + 1 = 1 + 1 = 2

n = 2, a n + 1 = a n + 1 ⇒ a 3 = a 2 + 1 = 2 + 1 = 3

n = 3, a n + 1 = a n + 1 ⇒ a 4 = a 3 + 1 = 3 + 1 = 4

n = 4, a n + 1 = a n + 1 ⇒ a 5 = a 4 + 1 = 4 + 1 = 5

Для нахождения каждого следующего члена последовательности требуется знать предыдущий.

n = 1, a n + 1 = ( a n + 1 ) 2 ⇒ a 2 = ( a 1 + 1 ) 2 = ( 1 + 1 ) 2 = 2 2 = 4

n = 2, a n + 1 = ( a n + 1 ) 2 ⇒ a 3 = ( a 2 + 1 ) 2 = ( 4 + 1 ) 2 = 3 2 = 9

n = 3, a n + 1 = ( a n + 1 ) 2 ⇒ a 4 = ( a 3 + 1 ) 2 = ( 9 + 1 ) 2 = 4 2 = 16

n = 4, a n + 1 = ( a n + 1 ) 2 ⇒ a 5 = ( a 4 + 1 ) 2 = ( 16 + 1 ) 2 = 5 2 = 25

a n + 1 = a n + 1 ⇒ a 2 = a 1 + 1 = − 3 + 1 = − 2 ; − 2 ≤ 3

a n + 1 = a n + 1 ⇒ a 3 = a 2 + 1 = − 2 + 1 = − 1 ; − 1 ≤ 3

a n + 1 = a n + 1 ⇒ a 4 = a 3 + 1 = − 1 + 1 = 0 ; 0 ≤ 3

a n + 1 = a n + 1 ⇒ a 5 = a 4 + 1 = 0 + 1 = 1 ; 1 ≤ 3

a n + 1 = a n + 1 ⇒ a 6 = a 5 + 1 = 1 + 1 = 2 ; 2 ≤ 3

a n + 1 = a n + 1 ⇒ a 7 = a 6 + 1 = 2 + 1 = 3 ; 3 ≤ 3

a n + 1 = a n + 1 ⇒ a 8 = a 7 + 1 = 3 + 1 = 4 ; 4 ≤ 3

Арифметическая прогрессия

Арифметической прогрессией < a n >называют числовую последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же для данной последовательности числом.

Разностью d арифметической прогрессии называют число, которое каждый раз прибавляют к предыдущему числу.

a 2 = a 1 + d a 3 = a 2 + d … a n = a n − 1 + d

Арифметическая прогрессия может быть

Примеры арифметической прогрессии:

Формулы арифметической прогрессии

(3) a n = a 1 + ( n − 1 ) d

Сумма n первых членов:

(4) S n = a 1 + a n 2 ⋅ n

(5) a n = a n − 1 + a n + 1 2

(6) a n = a n − k + a n + k 2

Геометрическая прогрессия

Геометрической прогрессией < b n >называют числовую последовательность, каждый член которой, начиная со второго, равен предыдущему, умноженному на одно и то же данной последовательности число.

Знаменателем q геометрической прогрессии называют число, на которое каждый раз умножают предыдущее число.

Геометрическая прогрессия может быть

Примеры геометрической прогрессии:

Формулы геометрической прогрессии

(3) b n = b 1 ⋅ q n − 1

Сумма n первых членов:

(4) S n = b 1 ⋅ ( q n − 1 ) q − 1

(5) b n = b n − 1 ⋅ b n + 1

(6) b n = b n − k ⋅ b n + k

Задание №12 из ОГЭ 2020. Типовые задачи и принцип их решения.

Источник

math4school.ru

Арифметическая и геометрическая прогрессии

Числовые последовательности (основные понятия)

Если каждому натуральному числу n поставить в соответствие действительное число a_n , то говорят, что задано числовую последовательность :

Итак, числовая последовательность — функция натурального аргумента.

Чтобы задать последовательность, нужно указать способ, позволяющий найти член последовательности с любым номером.

последовательность положительных нечётных чисел можно задать формулой

а последовательность чередующихся 1 и –1 — формулой

Последовательность можно определить рекуррентной формулой, то есть формулой, которая выражает любой член последовательности, начиная с некоторого, через предыдущие (один или несколько) члены.

последовательность двузначных натуральных чисел:

Последовательность простых чисел:

Монотонными последовательностями, в частности, являются возрастающие последовательности и убывающие последовательности.

Арифметическая прогрессия

Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему, к которому прибавляется одно и то же число.

является арифметической прогрессией, если для любого натурального числа n выполняется условие:

где d — некоторое число.

Таким образом, разность между последующим и предыдущим членами данной арифметической прогрессии всегда постоянна:

Чтобы задать арифметическую прогрессию, достаточно указать её первый член и разность.

найдём тридцатый член арифметической прогрессии

a_n =	a_n–1 + a_n+1
	2

каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому предшествующего и последующего членов.

Так как верно и обратное утверждение, то имеет место следующее утверждение:

числа a, b и c являются последовательными членами некоторой арифметической прогрессии тогда и только тогда, когда одно из них равно среднему арифметическому двух других.

Воспользуемся приведённым выше утверждением. Имеем:

a_n+1 + a_n–1	=	2n – 5 + 2n – 9	= 2n – 7 = a_n,
2		2

что и доказывает нужное утверждение. ◄

a_n =	a _n–k + a _n+k
	2

любой член арифметической прогрессии, начиная со второго равен полусумме равноотстоящих от него членов этой арифметической прогрессии.

Кроме того, для любой арифметической прогрессии справедливо равенство:

первых n членов арифметической прогрессии равна произведению полусуммы крайних слагаемых на число слагаемых:

Отсюда, в частности, следует, что если нужно просуммировать члены

то предыдущая формула сохраняет свою структуру:

Если дана арифметическая прогрессия, то величины a₁, a_n, d, n и S _n связаны двумя формулами:

a_n = a₁ + (n – 1)d и S_n =	a₁ + a_n	· n .
	2

Поэтому, если значения трёх из этих величин даны, то соответствующие им значения двух остальных величин определяются из этих формул, объединённых в систему двух уравнений с двумя неизвестными.

Арифметическая прогрессия является монотонной последовательностью. При этом:

Геометрическая прогрессия

Геометрической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему, умноженному на одно и то же число.

является геометрической прогрессией, если для любого натурального числа n выполняется условие:

где q ≠ 0 — некоторое число.

Таким образом, отношение последующего члена данной геометрической прогрессии к предыдущему есть число постоянное:

Чтобы задать геометрическую прогрессию, достаточно указать её первый член и знаменатель.

каждый член геометрической прогрессии, начиная со второго, равен среднему геометрическому (пропорциональному) предшествующего и последующего членов.

Так как верно и обратное утверждение, то имеет место следующее утверждение:

числа a, b и c являются последовательными членами некоторой геометрической прогрессии тогда и только тогда, когда квадрат одного из них равен произведению двух других, то есть одно из чисел является средним геометрическим двух других.

что и доказывает нужное утверждение. ◄

квадрат любого члена геометрической прогрессии, начиная со второго равен произведению равноотстоящих от него членов этой прогрессии.

Кроме того, для любой геометрической прогрессии справедливо равенство:

первых n членов геометрической прогрессии со знаменателем q ≠ 0 вычисляется по формуле:

S_n = b_{1 ·}	1 – q n	.
	1 – q

А при q = 1 — по формуле

Заметим, что если нужно просуммировать члены

то используется формула:

Если дана геометрическая прогрессия, то величины b₁, b_n, q, n и S_n связаны двумя формулами:

b_n = b₁ · q n –1 и S_n = b₁ ·	1 – q n	.
	1 – q

Поэтому, если значения каких-либо трёх из этих величин даны, то соответствующие им значения двух остальных величин определяются из этих формул, объединённых в систему двух уравнений с двумя неизвестными.

Для геометрической прогрессии с первым членом b₁ и знаменателем q имеют место следующие свойства монотонности :

Произведение первых n членов геометрической прогрессии можно рассчитать по формуле:

Бесконечно убывающая геометрическая прогрессия

Заметим, что бесконечно убывающая геометрическая прогрессия может не быть убывающей последовательностью. Это соответствует случаю

При таком знаменателе последовательность знакопеременная. Например,

Связь арифметической и геометрической прогрессий

Арифметическая и геометрическая прогрессии тесно связаны между собой. Рассмотрим лишь два примера.

Источник

Арифметическая и геометрическая прогрессии

Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом.

Формула суммы первых n членов арифметической прогрессии:

Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число.

В задачах на прогрессии важно:

Данная задача на геометрическую прогрессию, так как прибыль увеличивалась В четыре раза по сравнению с предыдущим годом.

Процент – это сотая доля числа.

Задачи на скидки:

Скидка — это понижение цены товара или услуги. Чаще всего скидку указывают в процентах.

Чтобы найти цену товара с учетом скидки необходимо:

$<4500·80>/<100>=3600$ рублей- это цена куртки, после скидки.

Задачи на смеси и сплавы.

В задачах на растворы и сплавы для удобства решения можно делать схему, для каждого раствора в схеме необходимо записать две величины:

Потом, если мы смешиваем составы, для смешанного вещества тоже записываем:

Далее составляем уравнение, для этого надо процентное содержание чистого вещества умножить на массу своего раствора, сложить получившиеся величины каждого раствора и все это приравнять к полученной величине смеси.

Составим к задаче схему.

$15%·2+10%·8=х%·10$ Уберем в уравнении знак процента, чтобы он не мешал при расчетах

Задачи на сложные проценты.

Формула сложных процентов связывает четыре величины:

Зная три величины, всегда можно найти четвертую:

В данной задаче воспользуемся формулой сложных процентов.

Подставим известные величины в формулу

В данной задаче воспользуемся формулой сложных процентов.

Так как цена на товар не увеличивалась, а уменьшалась, то формулу необходимо изменить

Источник

Прогрессии и последовательности: решаем ОГЭ по математике

Григорий Грянников

Тема «прогрессии» на ОГЭ тесно связана с понятием «последовательность». Если ученики понимают, как числа в последовательности связаны друг с другом, они легко справляются с заданиями. Сейчас мы разберем прогрессии — одну из самых коварных тем ОГЭ по математике. Обратите внимание: в этом материале все самое главное для решения ОГЭ, никакой воды!

Что такое последовательность?

В жизни мы очень часто сталкиваемся с математическими последовательностями и прогрессиями, буквально, каждый день, сами того не замечая. Однако встреча не всегда может быть приятной, особенно если она происходит на экзамене.

Последовательность – это набор элементов множества, который удовлетворяет следующим условиям:

Хочешь круто подготовится к ОГЭ? Тебе поможет учебный центр MAXIMUM! Все наши преподаватели сами сдавали этот экзамен на хороший балл. Мы ежегодно изучаем изменения ФИПИ и корректируем курсы, исходя из этого. Читай подробнее про наши курсы и выбирай подходящий!

Какие виды последовательности бывают?

Различают следующие виды последовательности:

Что такое арифметическая прогрессия?

Давайте посмотрим на следующий ряд чисел:

Что же у них может быть общего? Во-первых, все они нечетные, во-вторых, каждое следующее число мы можем получить из предыдущего, прибавляя к нему одно и то же число. Назовем это число d. В нашем случае d=2.

Описанная выше последовательность называется арифметической прогрессией. Получаем определение:

Приведем основные формулы:

Сумма первых n членов прогрессии можно вычислить по формуле:

Также арифметическая прогрессия обладает характерным свойством:

Как решать задачи ОГЭ на арифметическую прогрессию?

Теория — это прекрасно, но каждую теоретическую тему необходимо закреплять на практике. Сейчас мы разберем пару заданий ОГЭ по арифметической прогрессии.

Например, на ОГЭ может попасться вот такое задание:

Решение:

Ура! Первый прототип задания, который может встретиться на реальном экзамене, успешно выполнен. Идем дальше.

Решение:

Вот и все! Ничего сложного, учитывая то, что формула суммы первых n членов прогрессии есть в справочных материалах, которые выдаются на экзамене.

Что такое геометрическая прогрессия?

Геометрической прогрессией называется последовательность чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число q – знаменатель прогрессии. Элементы геометрической прогрессии можно задать соотношением:

Вот основные формулы для геометрической прогрессии:

Также геометрическая прогрессия, как и арифметическая, обладает характерным свойством:

Как решать задачи ОГЭ на геометрическую прогрессию?

Закрепим материал на практике и разберем две задачи ОГЭ по геометрической прогрессии.

Как видите, со знанием формул любое задание становится несложным!

В каком задании ОГЭ могут встретиться прогрессии?

Тема «Прогрессия» встречается в задании ОГЭ под номером 12. Выполнение этого задания экзаменуемым зависит от уровня сложности самого задания. В среднем с ним справляется всего 47% школьников. Как видите, сама тема не очень сложная. Все можно решить — достаточно правильно и хорошо подготовиться.

Напомним, что в КИМах с инструкцией и заданиями есть вспомогательные формулы, которые помогут при решении нашей задачи на прогрессию.

Теперь вы знаете теорию по теме прогрессии на ОГЭ. Можете смело оттачивать знания на практике. Пусть ваша встреча с прогрессиями на экзамене будет не печальной, а победной!

Хотите разобраться в других темах ОГЭ? Боитесь, что экзамены уже в следующем году, а вы даже не открывали учебники? Начните готовиться к ОГЭ-2021 уже сейчас на курсах с MAXIMUM. Мы поможем закрыть пробелы и сдать все на отлично. Правильная и интересная подготовка — залог успеха на экзаменах. Консультация бесплатно!

Источник

Арифметическая прогрессия свойства и формулы

Определение числовой последовательности

Числовая последовательность — это множество чисел, каждому из которых можно присвоить уникальный номер.

Последовательности можно задавать разными способами:

«Последовательность простых чисел: 4, 6, 10, 19, 21, 33. »

Последовательность y_n = C называют постоянной или стационарной.

Арифметическая прогрессия — (a_n), задана таким соотношением:
a₁ = a, a_n+1= a_n + d.

Последовательность Фибоначчи — когда каждое следующее число равно сумме двух предыдущих чисел: a_n+1 = a_n + a_n-1.

Пример: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55.

Так как алгебраическая числовая последовательность — это частный случай числовой функции, то ряд свойств функций рассматриваются и для последовательностей.

Свойства числовых последовательностей:

Возрастающие и убывающие последовательности называют монотонными последовательностями.

Пример числовой последовательности выглядит так:

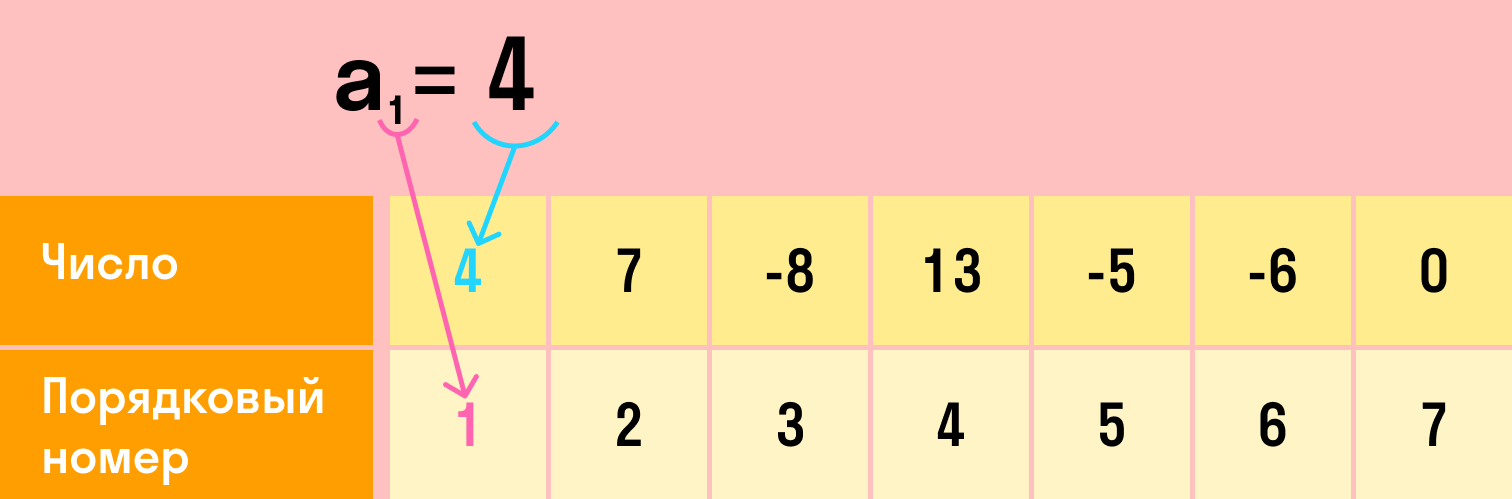
В такой математической последовательности каждый номер соответствует одному числу. Это значит, что в последовательности не может быть двух первых чисел и т.д. Первое число (как и любое другое) — всегда одно.

N-ный член алгебраической последовательности — это число с порядковым номером n.

Всю последовательность можно обозначить любой буквой латинского алфавита, например, a. Каждый член этой последовательности — той же буквой с индексом, который равен номеру этого члена: a₁, a₂. a₁₀. a_n.

N-ый член последовательности можно задать формулой. Например:

Определение арифметической прогрессии

Так как числовая последовательность — это частный случай функции, которая определена на множестве натуральных чисел, арифметическую прогрессию можно назвать частным случаем числовой последовательности.

Рассмотрим основные определения и как найти арифметическую прогрессию.

Арифметическая прогрессия — это числовая последовательность a₁, a₂. a_n. для которой для каждого натурального n выполняется равенство:

a_n+1= a_n + d, где d — это разность арифметической прогрессии.

Описать словами эту формулу можно так: каждый член арифметической прогрессии равен предыдущему, сложенному с одним и тем же числом d.

Разность между последующим и предыдущим членами, то есть разность арифметической прогрессии можно найти по формуле:

Если известны первый член a₁ и n-ый член прогрессии, разность можно найти так:

Арифметическая прогрессия бывает трех видов:

Пример: последовательность чисел 11, 14, 17, 20, 23. — это возрастающая арифметическая прогрессия, так как ее разность d = 3 > 0.

Свойство арифметической прогрессии

Переведем с языка формул на русский: каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому двух соседних с ним членов. Что как раз объясняет название «арифметическая» прогрессия.

Рассмотрим пример арифметической прогрессии.

Дано: арифметическая прогрессия (a_n), где a₁ = 0 и d = 2.

Найти: первые пять членов прогрессии и десятый член прогрессии.

Решение арифметической прогрессии:

По условиям задачи n = 10, подставляем в формулу:

Формулы арифметической прогрессии

В 9 классе проходят все формулы арифметической прогрессии. Давайте узнаем, какими способами ее можно задать:

Сумма первых n членов арифметической прогрессии (а_n) обозначается S_n:

Формулы нахождения суммы n членов арифметической прогрессии:

Чтобы быстрее запомнить формулы можно использовать такую табличку с основными определениями:

Формула n-го члена арифметической прогрессии

Из определения арифметической прогрессии следует, что равенство истинно:

Значит,

Переведем с языка формул на русский: если мы знаем первый член и разность арифметической прогрессии, то можем найти любой ее член.

Арифметическую прогрессию можно назвать заданной, если известен ее первый член и разность.

Доказательство формулы n-го члена арифметической прогрессии

Формулу n-го члена арифметической прогрессии можно доказать при помощи метода математической индукции.

Пусть дано:

Нужно доказать:

Действительно,

Согласно принципу математической индукции формула верна для любого натурального числа.

Геометрическая прогрессия

Геометрическая прогрессия — это последовательность (b_n), в которой каждый последующий член можно найти, если предыдущий член умножить на одно и то же число q.

Если последовательность (b_n) является геометрической прогрессией, то для любого натурального значения n справедлива зависимость:

b_n+1 = b_n * q, где q — знаменатель геометрической прогрессии

Если в геометрической прогрессии (b_n) известен первый член b₁ и знаменатель q, то можно найти любой член прогрессии:

Общий член геометрической прогрессии bn можно вычислить при помощи формулы:

Пример 1. 2, 6, 18, 54,… — геометрическая прогрессия b = 2, q = 3.

Пример 3. 7, 7, 7, 7,… — геометрическая прогрессия b = 7, q = 1.

Источник