что такое big o как происходит оценка асимптотической сложности алгоритмов
Сложность алгоритмов. Big O. Основы.
Развитие технологий привело к тому, что память перестала быть критическим ресурсом. Поэтому когда говорят об анализе сложности алгоритма, обычно подразумевают то, насколько быстро он работает.
Но ведь время выполнения алгоритма зависит от того, на каком устройстве его запустить. Один и тот же алгоритм запущенный на разных устройствах выполняется за разное время.
Big O показывает верхнюю границу зависимости между входными параметрами функции и количеством операций, которые выполнит процессор.
Распространённые сложности алгоритмов
Здесь рассмотрены именно распространённые виды, так как рассмотреть все варианты врядли возможно. Всё зависит от алгоритма, который вы оцениваете. Всегда может появится какая-то дополнительная переменная (не константа), которую необходимо будет учесть в функции Big O.
Означает, что вычислительная сложность алгоритма не зависит от входных данных. Однако, это не значит, что алгоритм выполняется за одну операцию или требует очень мало времени. Это означает, что время не зависит от входных данных.
Пример № 1.
У нас есть массив из 5 чисел и нам надо получить первый элемент.
Насколько возрастет количество операций при увеличении размера входных параметров?
Нинасколько. Даже если массив будет состоять из 100, 1000 или 10 000 элементов нам всеравно потребуется одна операция.
Пример № 2.
Сложение двух чисел. Функция всегда выполняет константное количество операций.
Пример № 3.
Размер массива. Опять же, функция всегда выполняет константной количество операций.
Означает, что сложность алгоритма линейно растёт с увеличением входных данных. Другими словами, удвоение размера входных данных удвоит и необходимое время для выполнения алгоритма.
Такие алгоритмы легко узнать по наличию цикла по каждому элементу массива.
Пример № 3.
Означает, что сложность алгоритма растёт логарифмически с увеличением входных данных. Другими словами это такой алгоритм, где на каждой итерации берётся половина элементов.
К алгоритмам с такой сложностью относятся алгоритмы типа “Разделяй и Властвуй” (Divide and Conquer), например бинарный поиск.
Означает, что удвоение размера входных данных увеличит время выполнения чуть более, чем вдвое.
Примеры алгоритмов с такой сложностью: Сортировка слиянием или множеством n элементов.
Означает, что удвоение размера входных данных увеличивает время выполнения в 4 раза. Например, при увеличении данных в 10 раз, количество операций (и время выполнения) увеличится примерно в 100 раз. Если алгоритм имеет квадратичную сложность, то это повод пересмотреть необходимость использования данного алгоритма. Но иногда этого не избежать.
Такие алгоритмы легко узнать по вложенным циклам.
Пример № 1.
В функции есть цикл в цикле, каждый из них проходит массив длиной n, следовательно сложность будет: O(n * n) = O(n 2 )
Зачем изучать Big O
Шпаргалка
Небольшие подсказки, которые помогут определить сложность алгоритма.
Полезные ссылки
Асимптотическая сложность алгоритмов: что за зверь?
Асимптотическая сложность алгоритмов встречается повсеместно. Доступно рассказываем, что это такое, где и как используется.
Асимптотическая сложность алгоритмов представляет собой время и память, которые понадобятся вашей программе в процессе экзекуции. Одно дело – знать, что существуют линейные или логарифмические алгоритмы, но совсем другое – понимать, что же за всем этим стоит.
С помощью Big O Notation можно математически описать то, как поведет себя программа в условиях наихудшего сценария при большом количестве входных данных. Например, если вы используете сортировку пузырьком, чтобы отсортировать элементы в целочисленном массиве по возрастанию, то худшим сценарием в этом случае будет отсортированный в убывающем порядке массив. При таком раскладе вашему алгоритму понадобится наибольшее количество операций и памяти.
Разобравшись в принципе работы Big O Notation, вы сможете решить проблему оптимизации ваших программ и добиться максимально эффективного кода.
Сложности О(1) и O(n) самые простые для понимания.
О(1) означает, что данной операции требуется константное время. Например, за константное время выполняется поиск элемента в хэш-таблице, так как вы напрямую запрашиваете какой-то элемент, не делая никаких сравнений. То же самое относится к вызову i-того элемента в массиве. Такие операции не зависят от количества входных данных.
Например, если у вас есть отсортированный массив, насчитывающий 8 элементов, в худшем случае вам понадобится сделать Log_2(8)=3 сравнений, чтобы найти нужный элемент.
Рассмотрим отсортированный одномерный массив с 16 элементами:
Допустим, нам нужно найти число 13.
Мы выбираем медиану массива и сравниваем элемент под индексом 7 с числом 13.
Так как наш массив отсортирован, а 16 больше, чем 13, мы можем не рассматривать элементы, которые находятся под индексом 7 и выше. Так мы избавились от половины массива.
Дальше снова выбираем медиану в оставшейся половине массива.
Сравниваем и получаем, что 8 меньше, чем 13. Уменьшаем массив вдвое, выбираем элемент посередине и делаем еще одно сравнение. Повторяем процесс, пока не останется один элемент в массиве. Последнее сравнение возвращает нужный элемент. Лучшее развитие событий – если первая выбранная медиана и есть ваше число. Но в худшем случае вы совершите log_2(n) сравнений.
То же самое произойдет, если вам надо будет пройтись по элементам двумерного массива.
Использование алгоритмов, которые работают в O(n^2) и выше (например, экспоненциальная функция 2^n ), является плохой практикой. Следует избегать подобных алгоритмов, если хотите, чтобы ваша программа работала за приемлемое время и занимала оптимальное количество памяти.
Оценка сложности алгоритмов, или Что такое О(log n)
Авторизуйтесь
Оценка сложности алгоритмов, или Что такое О(log n)
Наверняка вы не раз сталкивались с обозначениями вроде O(log n) или слышали фразы типа «логарифмическая вычислительная сложность» в адрес каких-либо алгоритмов. И если вы хотите стать хорошим программистом, но так и не понимаете, что это значит, — данная статья для вас.
Оценка сложности
Сложность алгоритмов обычно оценивают по времени выполнения или по используемой памяти. В обоих случаях сложность зависит от размеров входных данных: массив из 100 элементов будет обработан быстрее, чем аналогичный из 1000. При этом точное время мало кого интересует: оно зависит от процессора, типа данных, языка программирования и множества других параметров. Важна лишь асимптотическая сложность, т. е. сложность при стремлении размера входных данных к бесконечности.
Примеры
O(n) — линейная сложность
Такой сложностью обладает, например, алгоритм поиска наибольшего элемента в не отсортированном массиве. Нам придётся пройтись по всем n элементам массива, чтобы понять, какой из них максимальный.
O(log n) — логарифмическая сложность
Простейший пример — бинарный поиск. Если массив отсортирован, мы можем проверить, есть ли в нём какое-то конкретное значение, методом деления пополам. Проверим средний элемент, если он больше искомого, то отбросим вторую половину массива — там его точно нет. Если же меньше, то наоборот — отбросим начальную половину. И так будем продолжать делить пополам, в итоге проверим log n элементов.
O(n 2 ) — квадратичная сложность
3–5 декабря, Онлайн, Беcплатно
Бывают и другие оценки по сложности, но все они основаны на том же принципе.
Аналогично проводят оценку и по памяти, когда это важно. Однако алгоритмы могут использовать значительно больше памяти при увеличении размера входных данных, чем другие, но зато работать быстрее. И наоборот. Это помогает выбирать оптимальные пути решения задач исходя из текущих условий и требований.
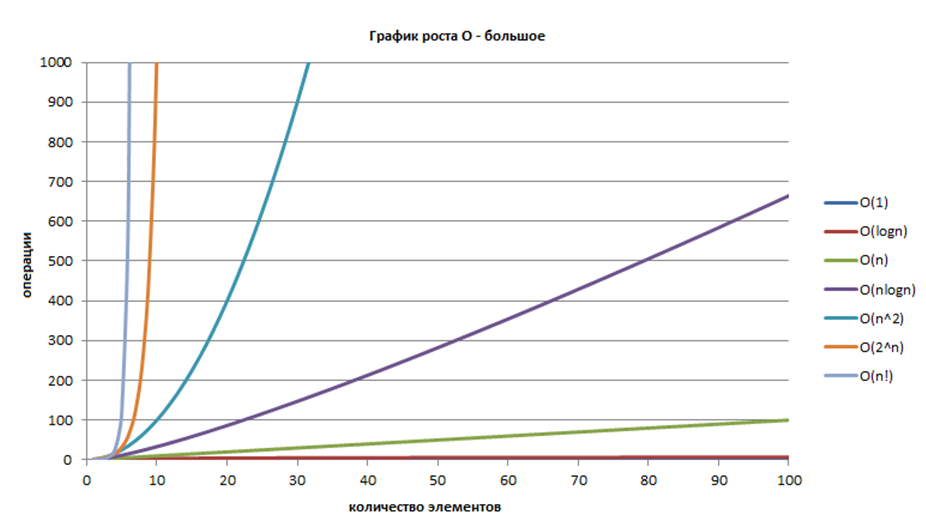
Наглядно
Время выполнения алгоритма с определённой сложностью в зависимости от размера входных данных при скорости 10 6 операций в секунду:
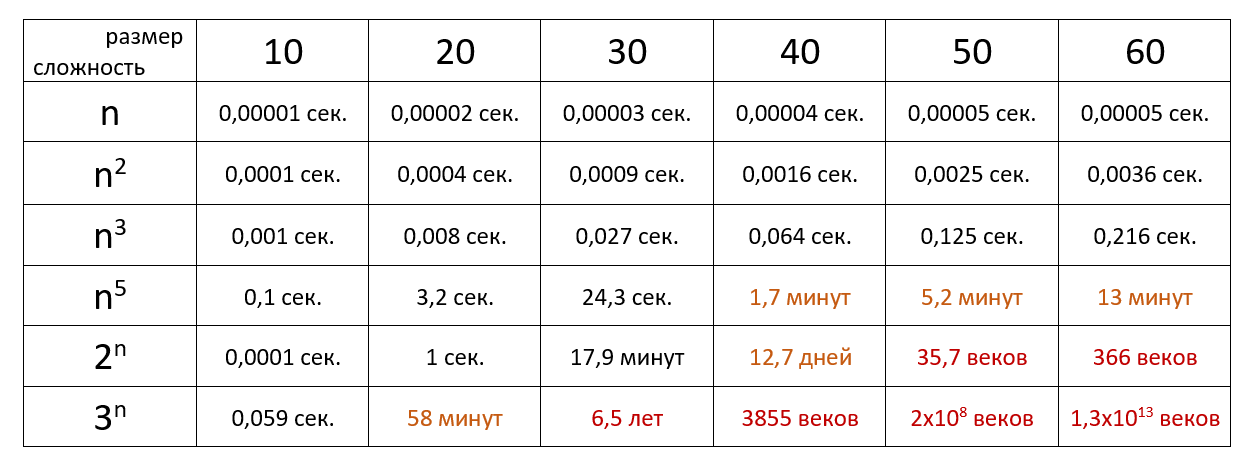
Если хочется подробнее и сложнее, заглядывайте в нашу статью из серии «Алгоритмы и структуры данных для начинающих».
6.1. Теория¶
Во время своей работы программы используют различные структуры данных и алгоритмы, в связи с чем обладают разной эффективностью и скоростью решения задачи. Дать оценку оптимальности решения, реализованного в программе, поможет понятие вычислительной сложности алгоритмов.
6.1.1. Основные понятия¶
Вычислительная сложность пытается ответить на центральный вопрос разработки алгоритмов: как изменится время исполнения и объем занятой памяти в зависимости от размера входных данных?. С помощью вычислительной сложности также появляется возможность классификации алгоритмов согласно их производительности.
В качестве показателей вычислительной сложности алгоритма выступают:
Временная сложность (время выполнения).
Временная сложность алгоритма зачастую может быть определена точно, однако в большинстве случаев искать точное ее значение бессмысленно, т.к. работа алгоритма зависит от ряда факторов, например, скорости процессора, набора его инструкций и т.д.
Асимптотическая сложность оценивает сложность работы алгоритма с использованием асимптотического анализа.
Алгоритм с меньшей асимптотической сложностью является более эффективным для всех входных данных.
6.1.2. Асимптотические нотации¶
Асимптотическая сложность алгоритма описывается соответствующей нотацией:
О-нотация, \(O\) («О»-большое): описывает верхнюю границу времени (время выполнения «не более, чем…»);
Омега-нотация, \(\Omega\) («Омега»-большое): описывает нижнюю границу времени (время выполнения «не менее, чем…»).
говорит о том, что алгоритм имеет квадратичное время выполнения относительно размера входных данных в качестве верхней оценки («О большое от эн квадрат»).
Каждая оценка при этом может быть:
наилучшая: минимальная временная оценка;
наихудшая: максимальная временная оценка;
средняя: средняя временная оценка.
При оценке, как правило, указывается наихудшая оценка.
Допустим, имеется задача поиска элемента в массиве. При полном переборе слева направо:
Наиболее часто используемой оценкой сложности алгоритма является верхняя (наихудшая) оценка, которая обычно выражается с использованием нотации O-большое.
Время выполнения не зависит от количества элементов во входном наборе данных.
Пример: операции присваивания, сложения, взятия элемента списка по индексу и др.
Время выполнения пропорционально количеству элементов в коллекции.
Пример: найти имя в телефонной книге простым перелистыванием, почистить ковер пылесосом и т.д.
Время выполнения пропорционально логарифму от количества элементов в коллекции.
Пример: найти имя в телефонной книге (используя двоичный поиск).
Время выполнения больше чем, линейное, но меньше квадратичного.
Пример: обработка \(N\) телефонных справочников двоичным поиском.
Время выполнения пропорционально квадрату количества элементов в коллекции.
Пример: вложенные циклы (сортировка, перебор делителей и т.д.).
6.1.3. Оценка сложности алгоритмов¶
Для оценки вычислительной сложности алгоритмов необходимо знать и учитывать сложности:
используемых структур данных;
совокупности различных операций.
6.1.3.1. Операции над структурами данных¶
В Python имеются коллекции (структуры данных), операции над которыми имеют определенную сложность.
6.1.3.1.1. Список и кортеж¶
Большинство операций со списком/кортежем имеют сложность \(O(N)\) (Таблица 6.1.1).
Понятие асимптотической сложности
Вступление
Наверное, каждый из нас на начальных этапах сталкивался с ситуацией вида “я решил эту задачу, но она не проходит по времени”. Это может озадачивать: вы написали то, что от вас требовалось по условию, проверили свой код, но решение почему-то не укладывается в ограничение по времени (о котором вы раньше даже не задумывались). Причина этого явления проста: вы перешли с уровня задач на “реализацию” на уровень задач на “идею”. Это значит, что просто написать то, что сказано в условии, теперь недостаточно. Вам нужно начать задумываться об эффективности вашего решения.
Другим важным параметром является количество использованной памяти, но оно редко становится ключевым для эффективности программы. Если ваше решение не укладывается в ограничение по памяти, оно скорее всего не уложится и в ограничение по времени.
Пример задачи
В качестве примера рассмотрим следующую задачу:
Дан массив из \(N\) натуральных чисел (\(N \le 10^6\)). Числа не превышают \(10^6\). Сколько пар равных чисел в нём содержится?
Казалось бы, что может быть проще? Недолго думая вы пишете код такого вида:
Преобразуем её, используя формулу суммы арифметической прогрессии:
В худшем случае это будет равно
Или примерно пятьсот миллиардов. Много, не так ли? В 2017-м году обычный процессор может выполнять на одном ядре примерно \(10^8\) операций в секунду. Стоит заметить, что не все операции равнозначны. С \(10^8\) операций сложения любой процессор справится без проблем, а, например, взятия квадратного корня, уже не каждый. Принимая производительность процессора за \(10^8\) операций/секунду, наша программа выполнится за каких-то \(5000\) секунд, примерно \(1.5\) часа. Стоит ли говорить, что это неприемлемо?
Как же решать эту задачу? Нужно придумать алгоритм, который будет работать гораздо быстрее. В таких ситуациях всегда нужно внимательно проанализировать ограничения на входные данные. Кроме ограничения на размер массива, у нас также ограничены сами числа: они не превышают \(10^6\). Можно ли это как-либо использовать? Да.
Значит, мы можем найти количество пар троек:
Посчитаем этот параметр для всех чисел и сложим получившиеся результаты. Это и будет ответом на задачу.
Как видите, мы уложились в два цикла, в худшем случае каждый из них выполнит по миллиону итераций, и общее число операций будет порядка \(3 * 10^6\). Значит, на том же процессоре наша программа будет выполняться за \(30\) мс, что уже гораздо лучше.
Асимптотическая сложность
На практике точно оценить время работы программы почти что невозможно. Даже если вы точно подсчитаете все элементарные операции (инструкции машинного кода) вашей программы, что уже неоправданно сложно, каждая инструкция выполняется процессором за разное количество тактов. Процессор часто выполняет несколько операций сложения за такт, а вот для операции деления требуется около десяти тактов. Время выполнения одного такта также может варьироваться (процессор не всегда работает на максимальной тактовой частоте). А если вспомнить про многопоточность и многоядерность, то перспективы окончательно омрачняются. Поэтому точным временем работы в информатике не оперируют.
Вместо этого используется зависимость времени работы от входных данных. Традиционно считается, что время работы прямо пропорционально количеству операций, так что эта зависимость отождествляется с зависимостью количества операций от входных данных.
В предыдущем разделе мы считали так называемое “примерное количество операций” наивного алгоритма. Посчитаем его ещё раз, в этот раз учитывая все операции, включая ввод-вывод и другие мелкие операции вне основных циклов, и выразим общее количество как функцию от размера массива \(N\):
То есть, принимая, что время работы прямо пропорционально количеству операций, время работы наивного алгоритма равно:
И формально означает следующее утверждение:
Существуют такие числа \(M\) и \(C\), что выполняется утверждение: \(f(x) M\).
Или, проще говоря, для достаточно больших \(x\), \(f(x)\) растёт медленнее \(g(x)\).
Применив такую запись к нашему времени работы мы получим:
Мы откинули члены \(N\) и \(c\), потому что при достаточно больших \(N\) они бесконечно малы по сравнению с \(N^2\). Деление на \(2\) откидывается, так как это, по сути, умножение на константу \(<1 \over 2>\), а константа нас не интересует при оценке скорости роста.
Вообще, так как “О большое” ограничивает рост функции только сверху, с таким же успехом можно сказать, что \(T(N) \in O(N^3)\), или \(T(N) \in O(N^4)\). Но на практике ограничение стараются подобрать как можно точнее, так что записи выше в каком-то смысле можно назвать некорректными, так как очевидно, что существует более точное ограничение.
Строго говоря, у зависимости времени работы от входных данных есть собственное название. Этот параметр называется асимптотической сложностью, или просто сложностью. Можно сказать, что сложность рассматриваемого алгоритма \(O(N^2)\), или что у алгоритма квадратичная сложность. На практике понятия “время работы”, “сложность” и “асимптотика” используются как взаимозаменяемые.
Используя новые термины, можно сказать, что у наивного решения этой задачи сложность \(O(N^2)\), а у оптимального \(O(N)\).
Часто сложность решения нельзя выразить через одну переменную, в таких случаях можно использовать функции от нескольких переменных: \(O(MN)\), \(O(N \log M)\), и так далее.
Для одной переменной чаще всего встречаются следующие значения сложности алгоритма:
Иногда нужно подчеркнуть, что несмотря на то, что два алгоритма имеют одинаковую сложность, один из них заметно эффективнее другого. В таких случаях говорят, что у такого алгоритма ниже константа.
Пессимистичная и средняя сложность
В нашем примере время работы наивного алгоритма не зависело от содержимого входного массива, а только от его размера. Для многих алгоритмов содержимое входных данных влияет на время работы, что не позволяет составить простую и точную функцию сложности.
В таких ситуациях чаще всего используются “не совсем точные” определения сложности, которые не учитывают конкретной структуры входных данных. Это либо пессимистичная сложность (англ. worst-case complexity), либо средняя сложность (англ. average complexity). В олимпиадных задачах важнее первое из них, и под словом “сложность” понимают имеют пессимистичную сложность.
Ограничение по времени и асимптотическая сложность
Перед тем, как ответить на этот вопрос, необходимо подчеркнуть, что метод, приведённый ниже, не имеет абсолютно никакого формального обоснования, и работает лишь в классических олимпиадных задачах. Никогда, ни в каких обстоятельствах нельзя применять его вне олимпиад.
Метод банально прост: пусть сложность нашего решения \(O(f(Input))\). Посчитаем максимальное значение \(f(Input)\) для всех входных данных. Чаще всего оно будет равно значению функции \(f\) для максимальных значений всех её параметров. Пусть ограничение по времени в задаче равно \(t\) секунд. Рассмотрим значение \(\max
Чем сложнее и нестандартнее задача, тем выше вероятность того, что метод может оказаться неточным или вовсе ошибочным. Особенно это касается решений задач, сложность которых сложно точно определить.
Оценка используемой памяти
Кроме времени работы, при решении задач также играет роль количество использованной памяти. Его тоже можно оценивать, используя асимптотические ограничения вида \(M(N) \in O(N)\), однако на практике это используется гораздо реже.
Чаще всего при решении задач, требующих использования большого количества памяти, близкого к ограничению, подавляющую часть используемой памяти будут занимать именно многомерные массивы/вектора. Хорошим методом при оценке используемой памяти будет отнять около 50 МБ от ограничения, и посчитать, хватает ли оставшейся памяти для основных массивов. Например, при ограничении 256 МБ можно спокойно создавать массивы, в сумме занимающие не более 200 МБ памяти.
Разумеется, такой метод применим только тогда, когда зависимость используемой памяти от входных данных тривиальна, и все большие контейнеры глобальны или “почти глобальны” (создаются при любых входных данных). Для более сложных задач нужно сначала проанализировать, какие входные данные будут пессимистичными, то есть приведут к максимальному использованию памяти.