что такое exp в формуле и как ее считать

Экспонента в математике – это функция «y=ex», которая отражает непрерывный рост с коэффициентом. В этой функции «е»‎ ‎– это число Эйлера, которое представляет собой постоянную (

2,72). Говоря иначе, рост любой величины прямо пропорционален ее значению.

Допустим, мы слепили снежный ком и спустили его с горы. Он начинает катиться, одновременно наращивая объем. При этом чем больше он становится, тем выше скорость его движения. И наоборот: чем быстрее он катится, тем быстрее увеличивается в размерах. Получается, что масса и скорость снежного кома (y) экспоненциально возрастают со временем (x).

Экспонента в жизни. Экспоненциальный рост

Рассмотрим примеры экспоненты и экспоненциального роста в реальной жизни.

Вклад в банке под процент. У всех процессов, идущих по экспоненте, есть одна особенность: за одно и то же количество времени их параметры меняются одинаковое количество раз.

Например, вклад в банке каждый год увеличивается на определенное количество процентов. Если положить 1000 рублей в банк под 10% годовых, то через год вклад будет составлять 1100 рублей. А в следующем году 10% будут начисляться уже исходя из суммы в 1100 рублей. То есть, вклад вырастет сильнее, и так размер прироста будет увеличиваться из года в год.

Численность животных. Чем больше популяция животных, тем больше они размножаются. Соответственно, рост численности популяции прямо пропорционален количеству особей в ней.

Чем экспоненциальный рост отличается от линейного?

Линейный рост характеризуется стабильным прибавлением постоянной, а экспоненциальный рост – это следствие многократного умножения на постоянную. То есть если линейный рост на графике представляет собой стабильную линию, то экспоненциальный рост характеризуется быстрым взлетом.

В качестве примера можно привести обычную ходьбу. Если длина одного шага составляет 1 метр, то через 6 шагов человек преодолевает расстояние в 6 метров. Это и называется линейным ростом.

При экспоненциальном росте длина каждого шага в нашем примере увеличивается в 2 раза. То есть сначала человек шагает на 1 метр, потом на 2 метра, потом на 4 метра и так далее. В таком случае за 6 шагов можно пройти 32 метра, что гораздо больше, чем в предыдущем примере.

Источник

Возведение экспоненты в степень

Экспонента (число e) — иррациональное число, приблизительно равное 2,71828. Число e играет большую роль в дифференциальном и интегральном исчислениях и используется практически во всех научных сферах. Столь сухое математическое определение совершенно не раскрывает сути о физическом смысле экспоненты. Рассмотрим подробнее.

Смысл числа e

Число Пи представляет собой не просто иррациональное число, равное 3,1415, а одинаковое для всех случаев соотношение длины окружности к диаметру. Точно так же и число e имеет свой собственный смысл.

Экспонента — это базовое соотношение роста для всех растущих процессов. Любое число можно рассматривать как увеличенную единицу, любой квадрат — как масштабированный единичный квадрат, любой равносторонний треугольник — как увеличенный или уменьшенный правильный треугольник, ну а любой коэффициент роста можно представить в виде масштабированного коэффициента е.

Именно операции с числом e дадут вам возможность определить темпы роста в таких ситуациях, как прирост населения, начисление процентов по депозиту или объем полураспада радиоактивного вещества.

Дискретный рост

В качестве базового примера системы непрерывного удвоения можно привести размножение бактерий, которые удваиваются каждые сутки. Если удвоение происходит один раз, то математически мы получаем 2 в первой степени, то есть просто 2. Если удвоений x раз, то в итоге мы получаем 2 в степени x бактерий, денег или любого другого добра.

Однако система может изменяться не в 2 раза, а например на 20% или 120%. В этом случае мы можем представить удвоение не как двойку, а как 1+1 или 1+100%. В такой записи мы можем подставить любой коэффициент прироста и получить формулу роста как:

где x — это количество циклов прироста.

Благодаря этой формуле мы можем узнать, сколько бактерий мы получим из одной клетки через 30 дней. Однако бактерии делятся дискретно, то есть пока новая клетка не сформируется в течение суток, она не сможет производить новые организмы. Применяя эту формулу к деньгам, мы получим совсем другой результат.

Непрерывный рост

При начислении процентов на деньги происходит не дискретный, а непрерывный рост. Как только по депозиту начисляется прибыль в размере пары пенни, эти деньги начинают приносить уже свою прибыль. Нет нужды ждать, пока «родится» целый доллар, который начнет делиться по подобию бактерий. Достаточно сформироваться центу, который начнет генерировать свою микроприбыль.

Доход = (1 + 0,5) 2 = 2,25

Так как у нас теперь два периода удвоения, мы возвели прирост в квадрат и получили дополнительные 25 центов дохода. Если разбить нашу прибыль на 5 частей по 20 центов, то получится еще привлекательнее:

Доход = (1 + 0,2) 5 = 2,4883

Может быть, мы сможем разделить прибыль на бесконечно большое количество мелких частей и получим бесконечную прибыль? Увы, нет. Даже если мы разделим наш доллар на 100 000 частей, доход составит:

Доход= (1 + 0,00001) 100 000 = 2,71826

При бесконечном дроблении доллара прибыль будет увеличиваться на стотысячные знаки после запятой. Наши 2,71826 доллара прибыли будут стремиться к значению 2,718281828, что есть ничто иное как число Е.

И что все это значит

Использование экспоненты на практике

На первый взгляд рост изображается в виде прибавления 1%, однако, математически такая прибавка выражается как умножение на 1,01. Таким образом, при операциях с числом e мы используем степени или корни. Или натуральные логарифмы, если нам необходима обратная операция. Какой бы коэффициент прироста мы не взяли, он будет означать степень для числа е. К примеру, если мы знаем, что в течение 3 лет получим прибыль в размере 200%, то мы просто умножаем прирост (e 2) на 3 периода и получаем:

Для лучшего понимания рассмотрим примеры.

Депозит в банке

Прибыль = 100 × е (0,08 × 5) = 149,1

Потрясающе, правда? К сожалению, реальные банки редко используют сложные проценты, а если и рассчитывают капитализацию, то по своим формулам, которые несколько отличаются от классической экспоненты.

Период полураспада

Представьте, что у вас есть 5 кг радиоактивного урана, который распадается со скоростью 100% в год. Сколько урана у вас останется через 2 года? По идее, весь уран должен распасться за первый же год, однако это не так. Через 6 месяцев у вас останется только 2,5 кг урана, который в свою очередь начнет распадаться со скоростью всего 2,5 кг в год. Еще через пару месяцев в вашем хранилище останется 1 кг урана, но и он будет распадаться с еще меньшей скоростью на уровне 1 кг в год. С течением времени вы теряете радиоактивное топливо, при этом снижается и скорость распада. Таким образом, через 2 года у вас останется:

Радиоактивный остаток = 5 × e −2 = 0,676

Заключение

Экспонента находит широкое применение в ситуациях, где что-либо непрерывно или дискретно растет. Вы можете использовать калькулятор возведения числа e в степень для подсчета результатов роста любых непрерывных процессов.

Источник

Математика для блондинок

Страницы

среда, 25 января 2012 г.

Экспонента на калькуляторе

Что такое экспонента и с чем её едят, мы разберемся в следующий раз. Сейчас мы разберемся, как где находится экспонента на калькуляторе и как её на калькуляторе считать. Нажимайте на ссылку, калькулятор откроется в новом окне. Приступим к практическим занятиям. Нажимайте на те же кнопочки, что нажимал я и смотрите на результат.

Для начала возведем число е в степень 4. В начале нужно набрать показатель степени. Нажимаем на кнопочку 4. Результат нашего вмешательства в беззаботную жизнь калькулятора можете посмотреть на картинке.

После этого нажимаем на специальную кнопочку экспоненты, обозначенную на калькуляторе е в степени х. Как видно из рисунка, калькулятор нас правильно понял и отреагировал именно так, как нам нужно.

Для вычисления заданного нами примера экспоненты необходимо нажать кнопочку равно.

Всё, мы получили требуемое значение.

Для начала вычислим е в первой степени. Собственно, это и будет значение числа е. Напомню, что любое число в первой степени равно самому себе. Порядок нажимания кнопочек пронумерован на картинке красными цифрами.

Мы получили округленное до 14 знаков после запятой значение числа е:

е 1 =е=2,71828182845905≈2,718

Число е подчиняется всем свойствам степени, как и любое другое число. Результаты возведения его в степень такие же, как у чисел больших единицы. При возведении в степень больше единицы результат будет больше первоначального. Для примера, возведем число е в не целую степень 9,876. Порядок нажимания кнопочек показан красными цифрами, результат виден на картинке.

Если показатель степени меньше единицы но больше нуля, то результат получится меньше первоначального но больше единицы. Это соответствует извлечению корня из числа е. Если на калькуляторе ввести показатель степени 0,5 (что равнозначно 1/2) то мы найдем квадратный корень числа е. Мы для примера возьмем экспоненту в степени 0,123

По логике, дальше следует показатель степени 0. Число е, как и любое другое число в нулевой степени, равняется единице. Это мы знаем и без калькулятора.

Мы получили число, обратное числу е:

Дальше пробуем добыть экспоненту со степенью меньше минус единицы.

Здесь полученный результат нужно преобразовать в удобоваримый для математиков вид. Делается это так:

Если после полученного на калькуляторе результата нажать ещё раз на знак равенства, десятичная дробь преобразуется в обычную дробь. Результат этой хитрой операции виден на картинке.

Но этот результат мне не нравится. Одна тысячная почти в два раза больше пяти десятитысячных. Если бы программа с калькулятором была русской, я бы подумал, что эту функцию писал бывший госслужащий, привыкший всё увеличивать в два раза (нужно же откуда-то себе воровать). Остается только предупредить, что и калькулятору полностью доверять нельзя, нужно самому анализировать результат, который он выдает.

В заключение найдем экспоненту с показателем степени больше минус единицы, но меньше нуля.

Теперь попробуем преобразовать результат в обычную дробь.

На этот раз калькулятор выдал более красивый результат. Но я уже ему не верю. Проверим результат преобразования, разделив на калькуляторе числитель на знаменатель. Результат деления записан ниже экспоненты.

Вот теперь можно поверить калькулятору, поскольку погрешность преобразования совсем незначительная. Округление даже до пяти знаков после запятой дает одинаковый результат.

Что делать, если вы пользуетесь виндосовским калькулятором и даже в инженерном варианте нет заветной кнопочки «е в степени икс»? Найдите кнопочку «Inv», рядом с ней есть кнопочка натурального логарифма «ln». Смело нажимайте кнопочку «Inv».

Экспонента на калькуляторе Виндовс картинка 1

После нажатия этой кнопочки, расположенная рядом кнопочка натурального логарифма волшебным образом превратится в кнопочку «число е в степени икс».

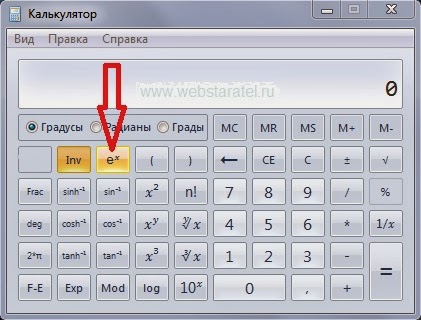Экспонента на калькуляторе Виндовс картинка 2

По замыслу создателей калькулятора, такие превращения натурального логарифма и ежу понятны. Но.

Во-первых. Ёжик должен быть трезвым.

Во-вторых. Ёжик должен быть сообразительным.

В третьих. В памяти ежа на первом месте должны бить свойства натуральных логарифмов, а не какая-то ерунда типа любви, смысла жизни или завтрашнего урока по математике.

Источник

Что такое Экспонента

Экспонента (экспоненциальная функция) — это математическая функция вида y = e×, или у = exp(x), или у = Exp(x) (где основанием степени является число е).

е — это число Эйлера, у него бесконечное количество цифр после запятой, оно трансцендентное и иррациональное. Оно равно округлённо 2,72 (а полностью — 2,718281828459045. ).

Трансцендентным число называется, если оно не удовлетворяет ни одному алгебраическому уравнению. Иррациональным — если его нельзя представить в виде дроби m/n, где n не равно 0.

Несмотря на свою бесконечность, число е является константой. То есть значением, которое никогда не изменяется.

Показательная функция — это математическая функция вида y = a×.

График экспоненты выглядит следующим образом:

Для чего используется экспонента?

Экспонента применяется и в физике, и в технике, и в экономике, особенно при решении задач, связанных с процентами.

Экспоненциальный рост

Мы используем термин экспоненциальный рост, чтобы сказать о стремительном росте чего-либо. Словосочетание чаще всего употребляется по отношению к росту популяции людей или животных/птиц.

Что такое второй замечательный предел

Швейцарский математик Якоб Бернулли (1655–1705 гг.) вывел число е, когда пытался решить финансовый вопрос. В частности, он пытался понять, как должны начисляться проценты на сумму вклада в банке, чтобы это было наиболее прибыльно для владельца денег.

Он также пытался понять, есть ли лимит у дохода, получаемого в процентах, или он будет увеличиваться бесконечно.

Решая эту задачу, он использовал предел последовательности, а именно второй замечательный предел. Формулу для вычисления числа е можно записать следующим образом (где n — это число, стремящееся к бесконечности):

То есть числу е равняется предел, где n стремится к бесконечности, от 1, плюс 1, разделённый на n, и всё возвести в степень n.

Если подставить в данную формулу вместо n какую-нибудь очень большую цифру, можно получить очень хорошее приближение к е.
Например, подставим 1.000.000 и посчитаем на калькуляторе:

(1 + 1/1000000) ^ 1000000 = 2.7182804691

Как видите, с n = 1.000.000 мы получили достаточно хорошее приближение, с правильными 5 знаками после запятой.

Как определить число е?

Помимо второго замечательного предела, существуют и другие способы для определения числа е:

Сумма ряда

Существует мнение, что этот метод использовал сам Эйлер, когда высчитывал е.

Можно получить приближение е, рассчитав первые 7 частей этой суммы:

И эти вычисления дали нам следующий результат:

Этот метод дал нам точных 4 знака после запятой, и его достаточно легко запомнить.

Формула Муавра — Стирлинга

Также называется просто формула Стирлинга:

И в этом случае чем больше n, тем точнее будет результат.

Как запомнить число е

Можно легко запомнить 9 знаков после запятой, если заметить удивительную закономерность: после «2,7» число «1828» появляется дважды (2,7 1828 1828). В 1828 году родились Лев Толстой и Жюль Верн, а Франц Шуберт умер.

Хотите дальше? Можно и дальше! 15 знаков после запятой! Последующие цифры — это градусы углов в равнобедренном прямоугольном треугольнике ( 45°, 90°, 45°): 2,7 1828 1828 45 90 45.

Интересные факты

Экспоненциальную функцию также называют экспонента.

Показательная функция — это функция вида y=a×, где a — заданное число (основание), x — это переменная.

А если основание = е, с переменной x, то математически логарифм записывается как ln, а не как log. И его называют натуральный логарифм (логарифм с основанием е):

Логарифмическая функция, что обратная к показательной функции y = a×, a > 0, a≠1, пишется как .

Производная и первообразная экспоненциальной функции равны ей самой, т. е. (e×)’ = e×, но (a×)’ = (a×)*ln(a).

Якобу Бернулли в расчётах помогал его брат Иоганн. Один из кратеров на Луне носит их имя.

Число Непера и число Эйлера

Число Непера или Неперово число, число Эйлера — это названия для одного и того же числа е.

Шотландский математик Джон Непер придумал логарифмы. Так как число е является основанием натурального логарифма (ln x), то этому числу присвоили имя математика из Шотландии. Хотя Непер и не вычислял его.

Сам символ e был придуман в 1731 году швейцарским математиком Леонардом Эйлером. Эйлер занимался вычислениями алгоритмов и вывел его основание. А точнее основание натурального логарифма, которым и является число е.

Изобретение логарифмов в XVII веке (1614 год) шотландским математиком Джоном Непером стало одним из важнейших событий в истории математики.

Источник

Для действительных чисел c и d функция формы также является экспоненциальной функцией, поскольку ее можно переписать как ж ( Икс ) знак равно а б c Икс + d <\ Displaystyle е (х) = ab ^ >

Экспоненциальную функцию иногда называют естественной экспоненциальной функцией, чтобы отличить ее от других экспоненциальных функций. Изучение любой экспоненциальной функции легко сводится к изучению естественной экспоненциальной функции, поскольку ж ( Икс ) знак равно е Икс <\ Displaystyle е (х) = е ^ <х>>

Как функции действительной переменной экспоненциальные функции однозначно характеризуются тем фактом, что скорость роста такой функции (то есть ее производной ) прямо пропорциональна значению функции. Константа пропорциональности этого отношения является натуральным логарифмом основания b :

Показательная функция удовлетворяет фундаментальному мультипликативному тождеству (которое также может быть расширено на комплексные показатели):

Аргументом экспоненциальной функции может быть любое действительное или комплексное число или даже математический объект совершенно другого типа (например, квадратная матрица ).

СОДЕРЖАНИЕ

Формальное определение

Посредством биномиальной теоремы и определения степенного ряда экспоненциальная функция также может быть определена как следующий предел:

Обзор

Производные и дифференциальные уравнения

Кроме того, для любой дифференцируемой функции f ( x ) по цепному правилу находим :

Непрерывные дроби для e x

или, применив замену z = Икс / у :

со специальным случаем для z = 2 :

Сложная плоскость

Как и в реальном случае, экспоненциальная функция может быть определена на комплексной плоскости в нескольких эквивалентных формах. Наиболее распространенное определение комплексной экспоненциальной функции аналогично определению степенного ряда для вещественных аргументов, где действительная переменная заменяется комплексной:

В качестве альтернативы, комплексная экспоненциальная функция может быть определена путем моделирования определения предела для реальных аргументов, но с заменой реальной переменной на сложную:

Определение комплексной экспоненциальной функции, в свою очередь, приводит к соответствующим определениям, расширяющим тригонометрические функции до сложных аргументов.

В частности, когда z = it ( t real), определение ряда дает разложение

В этом разложении преобразование членов в действительную и мнимую части оправдано абсолютной сходимостью ряда. Действительная и мнимая части приведенного выше выражения фактически соответствуют разложениям в ряды cos t и sin t соответственно.

Эти определения экспоненциальной и тригонометрической функций тривиально приводят к формуле Эйлера :

exp ⁡ ( я z ) знак равно потому что ⁡ z + я грех ⁡ z для всех z ∈ C <\ Displaystyle \ ехр (iz) = \ соз z + я \ грех Z <\ текст <для всех>> z \ in \ mathbb > .

Когда ее область определения расширяется от вещественной линии до комплексной плоскости, экспоненциальная функция сохраняет следующие свойства:

Затем мы можем определить более общее возведение в степень:

См. Отказ от тождества мощности и логарифма для получения дополнительной информации о проблемах с объединением степеней.

Источник