что такое grad в физике
Значение слова «градиент»
[От лат. gradiens, gradientis — шагающий]
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
, значение которой меняется от одной точки пространства к другой (скалярного поля), а по величине (модулю) равный скорости роста этой величины в этом направлении.
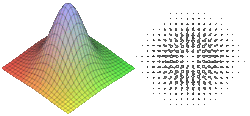
Например, если взять в качестве
высоту поверхности земли над уровнем моря, то её градиент в каждой точке поверхности будет показывать «направление самого крутого подъёма», и своей величиной характеризовать крутизну склона.
С математической точки зрения на градиент можно смотреть как на:
1. Коэффициент линейности изменения значения функции многих переменных от изменения значения аргумента
2. Вектор в пространстве области определения скалярной функции многих переменных, составленный из частных производных
3. Строки Матрицы Якоби содержат градиенты составных скалярных функций из которых состоит векторная функция многих переменных
Пространство, на котором определена функция и её градиент, может быть, вообще говоря, как обычным трёхмерным пространством, так и пространством любой другой размерности любой физической природы или чисто абстрактным (безразмерным).
Термин впервые появился в метеорологии, а в математику был введён Максвеллом в 1873 г. Обозначение grad тоже предложил Максвелл.
Градиент
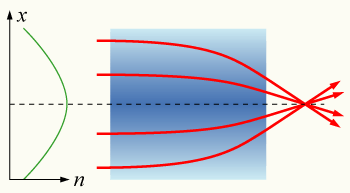
Например, если взять высоту поверхности Земли над уровнем моря (2-мерное пространство), то её градиент в каждой точке поверхности будет показывать «в горку» или многомодовое оптическое волокно, где в светопроводящем материале (например, в кврцевом стекле) использовано явление градиента коэффициента преломления n.
Содержание
Определение [ править | править код ]
Из определения градиента следует, что:
или, опуская по правилу Эйнштейна знак суммы,
(в ортонормированном базисе мы можем писать все индексы нижними, как мы и делали выше). Однако градиент оказывается настоящим ковариантным вектором в любых криволинейных координатах.
Пример [ править | править код ]
В физике [ править | править код ]
В различных отраслях физики используется понятие градиента различных физических полей.
Например, градиент концентрации — нарастание или уменьшение по какому-либо направлению концентрации растворённого вещества, градиент температуры — увеличение или уменьшение по направлению температуры среды, градиент коэффициента преломления n световых лучей в многомодовых воло́кнах (Волоконная оптика) и т. д. Градиент может быть вызван различными причинами, например, механическим препятствием, действием электромагнитных, гравитационных или других полей или различием в растворяющей способности граничащих фаз, например, октанол/вода.
Параболический градиент показателя преломления [ править | править код ]
Если показатель преломления среды не постоянен, но изменяется с определённым ускорением и когда известен материал, то это — оптический материал с градиентным профилем. Прохождение светового луча через такую среду может быть с изменением траектории волны (например, по параболе)или сосредоточено по прямой линии. Этот эффект используется при изготовлении линз, некоторых оптических волокон (многомодовых) и других оптических устройствах. Немного явлений — общих миражей также вызваны пространственно-переменным градиентным коэффициентом преломления n нагретового воздуха. [1] [2]
Геометрический смысл [ править | править код ]
Связь с производной по направлению [ править | править код ]
Таким образом, для вычисления производной по любому направлению достаточно знать градиент функции, то есть вектор, компоненты которого являются её частными производными.
СОДЕРЖАНИЕ
Мотивация
Обозначение
Определение
Когда функция также зависит от параметра, такого как время, градиент часто относится просто к вектору только его пространственных производных (см. Пространственный градиент ).
Декартовы координаты
В трехмерной декартовой системе координат с евклидовой метрикой градиент, если он существует, задается следующим образом:
Цилиндрические и сферические координаты
В цилиндрических координатах с евклидовой метрикой градиент задается следующим образом:
В сферических координатах градиент определяется как:
Общие координаты
Последнее выражение соответствует приведенным выше выражениям для цилиндрических и сферических координат.
Связь с производной
Связь с полной производной
С вычислительной точки зрения, учитывая касательный вектор, вектор можно умножить на производную (в виде матриц), что равносильно взятию скалярного произведения с градиентом:
( d ж п ) ( v ) знак равно [ ∂ ж ∂ Икс 1 ( п ) ⋯ ∂ ж ∂ Икс п ( п ) ] [ v 1 ⋮ v п ] знак равно ∑ я знак равно 1 п ∂ ж ∂ Икс я ( п ) v я знак равно [ ∂ ж ∂ Икс 1 ( п ) ⋮ ∂ ж ∂ Икс п ( п ) ] ⋅ [ v 1 ⋮ v п ] знак равно ∇ ж ( п ) ⋅ v <\ Displaystyle (df_
) (v) = <\ begin
Дифференциальная или (внешняя) производная
Наилучшее линейное приближение дифференцируемой функции
Градиент связан с дифференциалом формулой
Если R n рассматривается как пространство векторов-столбцов (размерности n ) (действительных чисел), то можно рассматривать df как вектор-строку с компонентами
Линейное приближение к функции
Связь с производной Фреше
Как следствие, обычные свойства производной сохраняются для градиента, хотя градиент сам по себе не является производной, а скорее двойственен производной:
Другие свойства и применения
Наборы уровней
В более общем смысле, любая вложенная гиперповерхность в римановом многообразии может быть вырезана уравнением вида F ( P ) = 0 таким, что dF нигде не равно нулю. Тогда градиент F нормален к гиперповерхности.
Консервативные векторные поля и градиентная теорема
Градиент функции называется градиентным полем. (Непрерывное) поле градиента всегда является консервативным векторным полем : его линейный интеграл вдоль любого пути зависит только от конечных точек пути и может быть вычислен с помощью градиентной теоремы (основная теорема исчисления для линейных интегралов). И наоборот, (непрерывное) консервативное векторное поле всегда является градиентом функции.
Обобщения
Якобиан
Градиент векторного поля
Поскольку полная производная векторного поля является линейным отображением векторов в векторы, это тензорная величина.
(где используется обозначение суммирования Эйнштейна, а тензорное произведение векторов e i и e k является диадическим тензором типа (2,0)). В целом это выражение равно транспонированной матрице Якоби:
В криволинейных координатах или, в более общем смысле, на изогнутом многообразии градиент включает символы Кристоффеля :
Выражаясь более инвариантно, градиент векторного поля f может быть определен связностью Леви-Чивиты и метрическим тензором:
Римановы многообразия
где X j обозначает j- й компонент X в этой координатной карте.
Итак, локальная форма градиента принимает вид:
Что такое grad в физике
Смотреть что такое «grad» в других словарях:
gråd — sb., en … Dansk ordbog
grad — GRAD, grade, s.n. 1. Nume dat mai multor unităţi de măsură pentru diverse mărimi (variabile), în cadrul unor sisteme sau scări de reper. Grad centezimal. Grad de latitudine. ♢ Grad de libertate = indice care arată posibilităţile de mişcare ale… … Dicționar Român
Grad — may refer to:* Grad (angle), a unit of angular measurement * Gradient of a scalar field, a differential operator in mathematics * Grad, a Soviet multiple launch rocket system * Graduation ceremony, prom, or a graduate * Grad Nite, a Disneyland… … Wikipedia
Grad — 〈m.; Gen.: (e)s, Pl.: e od. (bei Zahlenangaben) 〉 1. Abstufung, Stufe, Stärke, Maß; WirkungsGrad; Erfrierungen, Verbrennungen dritten Grades; einige Grade dunkler, heller; bis zu einem gewissen Grad(e); im höchsten Grade ärgerlich sehr,… … Lexikalische Deutsches Wörterbuch
grad — <><
Grad [1] — Grad, in der niederen Algebra der Exponent der höchsten in einer Gleichung vorkommenden Potenz der Unbekannten (eine Gleichung zweiten Grades heißt quadratisch u.s.w.). In der höheren Mathematik wird bei einem algebraischen Ausdruck (Form) der… … Lexikon der gesamten Technik
grad. — grad. 〈Abk. für〉 graduiert * * * grad. = graduiert. * * * grad., Abkürzung für graduiert; 1964 80 verliehener akademischer Grad, der in Verbindung mit einer näheren Bezeichnung der Fachrichtung seit 1964 von Absolventen der staatlich… … Universal-Lexikon
Grad — der (für Temperatureinheit meist: das); [e]s, e <lateinisch> (Temperatureinheit; Einheit für [ebene] Winkel [1º = 90. Teil eines rechten Winkels]; Zeichen º); 3 Grad C oder 3º C oder 3 ºC (fachsprachlich nur so); der 30. Grad (nicht: 30. º … Die deutsche Rechtschreibung
grad. — • grad. Grad. Die Wörter gerad[e] und Gerad[e] sowie die mit ihnen gebildeten Zusammensetzungen werden umgangssprachlich oft in den verkürzten Formen grad. oder Grad. verwendet, z. B. grade, Grade, gradeaus, gradestehen, gradezu,… … Die deutsche Rechtschreibung
Grad. — • grad. Grad. Die Wörter gerad[e] und Gerad[e] sowie die mit ihnen gebildeten Zusammensetzungen werden umgangssprachlich oft in den verkürzten Formen grad. oder Grad. verwendet, z. B. grade, Grade, gradeaus, gradestehen, gradezu,… … Die deutsche Rechtschreibung
Что такое grad в физике

Romkin © ( 2004-09-10 10:09 ) [1]
Градиент. Вектор, направленный в сторону наиболшего возрастания функции в данной точке. Его длина указывает скорость этого возрастания. Примечание: ручей с холма всегда течет обратно градиенту в любой своей точке.

Думкин © ( 2004-09-10 10:11 ) [2]
> [1] Romkin © (10.09.04 10:09)
> Примечание: ручей с холма всегда течет обратно градиенту в любой своей точке.
Какому градиенту?

olookin © ( 2004-09-10 10:12 ) [3]
grad(Ф) = d(Ф)/dx + d(Ф)/dy + d(Ф)/dz
для одномерного случая только d(Ф)/dx
Сообщите, если я неправ.

Romkin © ( 2004-09-10 10:14 ) [4]
Думкин © (10.09.04 10:11) [2] Градиенту потенциала гравитационного поля :)))
olookin © (10.09.04 10:12) [3] Я сказал вектор! А у тебя скалярная величина :))

olookin © ( 2004-09-10 10:18 ) [6]
[4] Romkin © (10.09.04 10:14)
Значит, я был неправ.

Romkin © ( 2004-09-10 10:19 ) [7]

Romkin © ( 2004-09-10 10:20 ) [8]
olookin © (10.09.04 10:18) [6] Почти прав
grad(Ф) = (d(Ф)/dx, d(Ф)/dy, d(Ф)/dz)

Думкин © ( 2004-09-10 10:23 ) [9]
Только наверное не форму, а такая функция H(x,y)

Romkin © ( 2004-09-10 10:36 ) [11]
Думкин © (10.09.04 10:24) [10] Ага. Hill(x,y) :)))

olookin © ( 2004-09-10 10:38 ) [12]
[8] Romkin © (10.09.04 10:20)
А вот тут ты не прав. Раз вектор представляется координатами, то надо и базисы отобразить.
> olookin © (10.09.04 10:38) [12]
> [8] Romkin © (10.09.04 10:20)
>
> А вот тут ты не прав. Раз вектор представляется координатами,
> то надо и базисы отобразить.
Добавь в [3] i, j, k и будет щасье:
> [13] DiamondShark © (10.09.04 11:26)
В строгом направлении? Или я неверно толкую слово противоположно?

dr Tr0jan ( 2004-09-10 11:38 ) [16]
А можно привести пример с конкретными числами7

Alx2 © ( 2004-09-10 11:44 ) [17]
На ручей, кроме гравитации, ещё какие-то силы действуют?

Думкин © ( 2004-09-10 11:56 ) [19]
> Думкин © (10.09.04 11:56) [19]
Так составляющая против градиента есть? Есть. В чём проблем?

Думкин © ( 2004-09-10 12:05 ) [21]

Думкин © ( 2004-09-10 12:08 ) [22]
> [20] DiamondShark © (10.09.04 12:04)
Есть, но все-таки не в противоположную. А с составляющей не равной 0. Только это.
Я тебе кстати предложил:
> Или я неверно толкую слово противоположно?
не зацепился. Ну и ладно.
> Думкин © (10.09.04 12:08) [22]
Об чём шумим? Не пойму.

Думкин © ( 2004-09-10 12:14 ) [24]
> [23] DiamondShark © (10.09.04 12:13)
Сам не знаю. 🙂
Кстати у автора в сабже Grad, а потом речь о grad. А это немного разные вещи. Если второе для скалярных функций, то первое для произвольных тензоров.

pasha_golub © ( 2004-09-10 12:29 ) [25]
А можно я немножко поламерю?
1. Разве grad єто функция? Это ж вроде оператор.
2. На ручей действует сила реакции опоры, ну в смысле холм опирается. Потому и в Каспийское море, а не в центр Земли.

Думкин © ( 2004-09-10 12:35 ) [26]

dr Tr0jan ( 2004-09-10 12:39 ) [27]
Ну ладно, допустим у меня есть конкретное численное значение напряжённости в данной точке, причём никаких функций не задано. А как мне найти значение потенциала в этой же точке (см. начало)?

pasha_golub © ( 2004-09-10 12:40 ) [28]
Думкин © (10.09.04 12:35) [26]
1. Ну оператор. Функция из одного множества в другое. Просто множества такие.
> причём никаких функций не задано.
Тогда курить бамбук. Оператор применим к скалярному полю, то бишь к функции, задающей пространственное распределение величины.
Только по значению напряжённости потенциал не определить.
Пример: поле в плоском конденсаторе. Напряжённость везде одинаковая, а потенциал разный.

Думкин © ( 2004-09-10 12:54 ) [31]