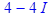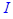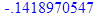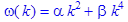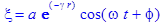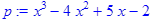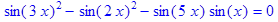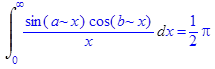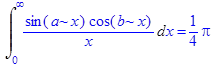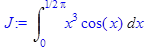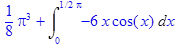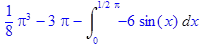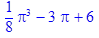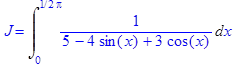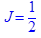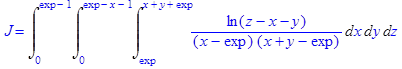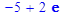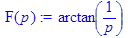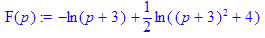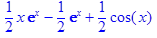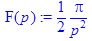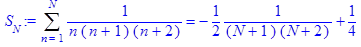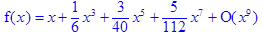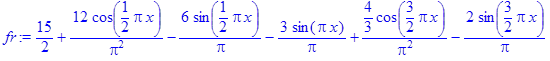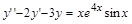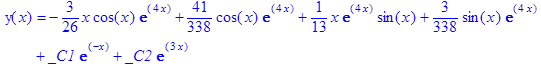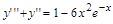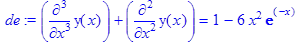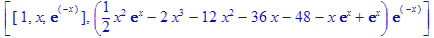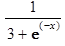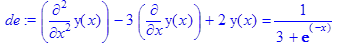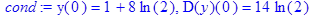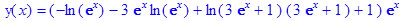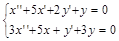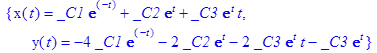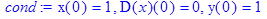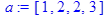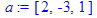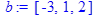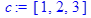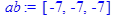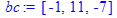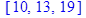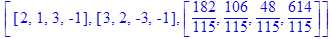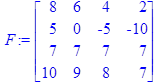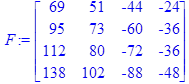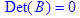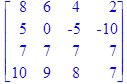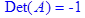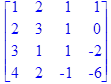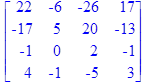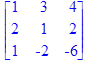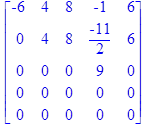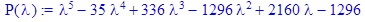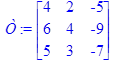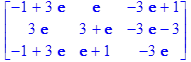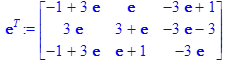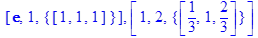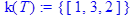что такое maple и для чего он предназначен
Что такое maple и для чего он предназначен
Maple V представляет собой один из наиболее мощных математических пакетов Его возможности охватывают достаточно много разделов математики и могут с пользой применяться на разных уровнях, включая и уровень серьезных научных исследований.
Работать с ним можно как в режиме интерактивного диалога, так и путем составления и отладки программ на специальном Maple-языке, ориентированном на сложные математические вычисления.
Maple умеет не только вычислять, но и обладает богатыми возможностями графического представления математических объектов и процессов.
Интерфейс пользователя
Здесь мы кратко рассмотрим лишь интерфейс пакета, работающего под Windows.
Окно Maple содержит многие атрибуты, привычные пользователю других приложений Windows: заголовочную часть, строку ниспадающих меню, панель управления, линейку вертикальной прокрутки, строку состояния и т.д. Основную часть базового окна занимает еще одно окно, в котором обычно располагаются один или несколько рабочих документов (Maple worksheet). В этом же окне могут располагаться окна помощи. Состояние ниспадающих и контекстного меню и кнопок на панели управления зависит от того, какое именно окно активно в настоящий момент и месторасположения курсора в окне Maple worksheet.
Исполняемые команды вводятся после специльного приглашения ‘ > ‘, красным цветом и должны заканчиваться точкой с запятой или двоеточием. Обычно команды вводятся в строчном формате, но пользователь имеет возможность перейти к специальному математическому формату ( который по умолчанию применяется при выводе). В одной строке может быть расположено более одной команды. Если после команды стоит двоеточие, то результат ее выполнения не будет отображен на экране. Если же после команды стоит точка с запятой, то после ее выполнения на экране появится результат. Если Maple не сможет вычислить введенное выражение, то результатом будет перевод введеннного выражения в матматический формат, принятый для вывода. Выходная информация печатается по умолчанию синим цветом. Исполнение Maple-команды инициируется нажатием ввода.
Текст черного цвета, которым написаны этот и предыдущие абзацы, используется для комментариев и никак не обрабатывается системой.
Для того чтобы вводить такой текст, достаточно, находясь в командной строке, нажать кнопку « Т « на панели управления, или вставить параграф, выбрав соответствющий пункт раздела «Insert» нисподающего меню.
С помощью пункта меню «HyperLink. » из раздела » I nsert» можно создавать ссылки на определенные разделы других рабочих документов и топиков помощи. Тем самым Maple-документ может обладать структурой гипертекста.
Первые примеры
Рассмотрим простейшие примеры работы с Maple в интерактивном режиме:
1. Краткая характеристика систем класса Maple
Краткая характеристика систем класса Maple
Назначение и место систем Maple
Maple — система компьютерной математики, рассчитанная на широкий круг пользователей. До недавнего времени ее называли системой компьютерной алгебры, Ито указывало на особую роль символьных вычислений и преобразований, которые способна осуществлять эта система. Но такое название сужает сферу применения системы. На самом деле она уже способна выполнять быстро и эффективно не только символьные, но и численные расчеты, причем сочетает это с превосходными средствами графической визуализации и подготовки электронных документов.
Казалось бы, нелепо называть такую мощную систему, как Maple 7 математической системой «для всех». Однако по мере ее распространения она становится полезной для многих пользователей ПК, вынужденных в силу обстоятельств (работа, учеба, хобби) заниматься математическими вычислениями и всем, что с ними связано. А все это простирается от решения учебных задач в вузах до моделирования сложных физических объектов, систем и устройств, и даже создания художественной графики (например, фракталов).
Для наших читателей (в том числе и для математиков-профессионалов) возможности систем символьной математики, реализованных на массовых ПК класса IBM PC, порой являются полной неожиданностью и вызывают вполне заслуженное удивление и восхищение, но иногда и резкое отрицание. Впрочем, последнее характерно скорее для тех, кто с системой Maple просто не работал и относится к ней, как дама из анекдота о паровозе — увидев паровоз впервые, она воскликнула: «Не может быть, что он едет без лошадей!» Maple — тщательно и всесторонне продуманная система компьютерной математики. Она с равным успехом может использоваться как для простых, так и для самых сложных вычислений и выкладок. Заслуженной популярностью системы Maple (всех версий) пользуются в университетах — свыше 300 самых крупных университетов мира (включая и наш МГУ) взяли эту систему на вооружение. А число только зарегистрированных пользователей системы уже давно превысило один миллион. Ядро системы Maple используется в ряде других математических систем, например в MATLAB и Mathcad, для реализации в них символьных вычислений.
Добавьте к этому куда большее число незарегистрированных пользователей — ведь система записана на многих компакт-дисках, лихо продаваемых в России по вполне доступным ценам. Если учесть все это, то оказывается, что популярность системы Maple ничуть не ниже, а то и выше, чем у гораздо более простых систем, таких как Derive и Mathcad. Вот и решайте, какая из систем и впрямь рассчитана на всех!
Maple — типичная интегрированная система. Она объединяет в себе:
Ко всем этим средствам имеется полный доступ прямо из программы. Maple — одна из самых мощных и «разумных» интегрированных систем символьной математики, созданная фирмой Waterloo Maple, Inc. (Канада).
Во многих обзорах систем компьютерной алгебры Maple справедливо считается одним из первых кандидатов на роль лидера среди них. Это лидерство она завоевывает в честной конкурентной борьбе с другой замечательной математической системой — Mathematica 4.1. Каждая из данных двух систем имеет свои особенности, но в целом эти две лидирующие системы практически равноценны. Однако надо отметить, что появление новейшей версии Maple 7 означает очередной виток в соревновании этих систем за место лидера мирового рынка. Причем виток на этот раз раньше сделала система Maple 7.
Система Maple прошла долгий путь развития и апробации. Она реализована на больших ЭВМ, рабочих станциях Sun, ПК, работающих с операционной системой Unix, ПК класса IBM PC, Macintosh и др. Все это самым положительным образом повлияло на ее отработку и надежность (в смысле высокой вероятности правильности решений и отсутствия сбоев в работе). Не случайно ядро системы Maple V используется целым рядом других мощных систем компьютерной математики, например системами класса Mathcad и MATLAB. А совсем недавно упрощенная версия Maple для операционной системы Windows СЕ стала использоваться в миниатюрных компьютерах фирмы Casio — Cassiopeia.
Что такое Maple и для чего он предназначен?
Лабораторная работа №1
Структура окна Maple. Арифметические операции, числа, константы и стандартные функции. Элементарные преобразования математических выражений.
Контрольные задания
1. Вычеслить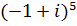 
,
2. Вычислить: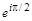 
.
> exp(I*Pi/2);
3. Вычислить точное и приближенное значения выражения: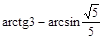 
.
> arccot(3.0)-arcsin(sqrt(5.0)/5.0);
> arccot(3)-arcsin(sqrt(5)/5);
4. Записать формулы: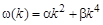 
; 
.
> omega(k)=alpha*k^2+beta*k^4; xi=a*exp(-gamma*r)*cos(omega*t+phi);
5. Разложить на множители полином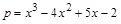 
.
> p:=x^3-4*x^2+5*x-2;
> factor(p);
6. Упростить выражение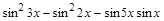 
.
> eq:=(sin(3*x))^2-(sin(2*x))^2-sin(5*x)*sin(x):
> eq=combine(eq,trig);
Контрольные вопросы.
Что такое Maple и для чего он предназначен?
Maple – это пакет для аналитических вычислений на компьютере, содержащий более двух тысяч команд, которые позволяют решать задачи алгебры, геометрии, математического анализа, дифференциальных уравнений, статистики, математической физики.
Опишите основные элементы окна Maple.
Maple представляет собой типичное окно Windows, которое состоит из Строки названия, Основного меню, Панели инструментов, Рабочего поля и Строки состояния, а также Линейки и Полос прокрутки.
На какие условные части делится рабочее поле Maple и что в этих частях отображается?
Рабочее поле разделяется на три части:
Как перевести командную строку в текстовую и наоборот?
Для того, чтобы переключить командную строку в текстовую, следует на Панели инструментов нажать мышью на кнопку 
.
Обратное переключение текстовой строки в командную осуществляется нажатием на Панели инструментов на кнопку 
В каком режиме проходит сеанс работы в Maple?
Работа в Maple проходит в режиме сессии – пользователь вводит предложения (команды, выражения, процедуры), которые воспринимаются условно и обрабатываются Maple.
Перечислите пункты основного меню Maple и их назначение.
Основное меню состоит из:
File (Файл) – содержит стандартный набор команд для работы с файлами, например: сохранить файл, открыть файл, создать новый файл и т.д.
Edit (Правка) – содержит стандартный набор команд для редактирования текста, например: копирование, удаление выделенного текста в буфер обмена, отмена команды и т.д.
View (Вид) – содержит стандартный набор команд, управляющих структурой окна Maple.
Insert (Вставка) – служит для вставки полей разных типов: математических текстовых строк, графических двух и трехмерных изображений.
Format (Формат) – содержит команды оформления документа, например: установка типа, размера и стиля шрифта.
Options (Параметры) – служит для установки различных параметров ввода и вывода информации на экран, принтер, например, таких как качество печати.
Windows (Окно) – служит для перехода из одного рабочего листа в другой.
Help (Справка) – содержит подробную справочную информацию о Maple.
Какое стандартное расширение присваивается файлу рабочего листа Maple?
Файлу рабочего листа Maple присваивается расширение .mws.
Как представляются в Maple основные математические константы?
Основные математические константы:
Pi – число ; I – мнимая единица i; infinity – бесконечность; Gamma – константа Эйлера; true, false – логические константы, обозначающие истинность и ложность высказывания.
Опишите виды представления рационального числа в Maple.
Рациональные числа могут быть представлены в 3-х видах:
1) рациональной дроби с использованием оператора деления, например: 28/70;
2) с плавающей запятой (float), например: 2.3;
3) в показательной форме, например: 1,602*10^(-19)
Лабораторная работа №2
Лабораторная работа №3
Построение графиков
Контрольные задания
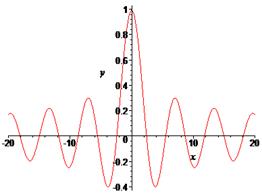
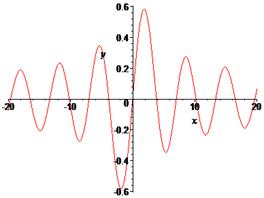
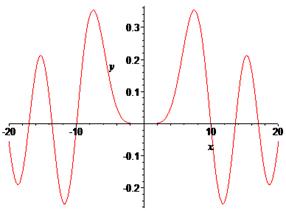
> plot(BesselJ(1,x),x=-20..20,labels=[x,y], labelfont =[TIMES,ITALIC,12]);
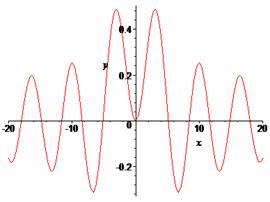
> plot(BesselJ(2,x),x=-20..20,labels=[x,y], labelfont =[TIMES,ITALIC,12]);
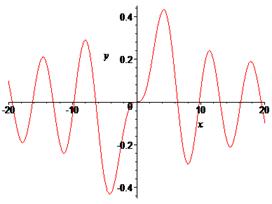
> plot(BesselJ(3,x),x=-20..20,labels=[x,y], labelfont =[TIMES,ITALIC,12]);
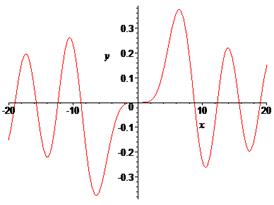
> plot(BesselJ(4,x),x=-20..20,labels=[x,y], labelfont =[TIMES,ITALIC,12]);
> plot(BesselJ(5,x),x=-20..20,labels=[x,y], labelfont =[TIMES,ITALIC,12]);
> plot(BesselJ(6,x),x=-20..20,labels=[x,y], labelfont =[TIMES,ITALIC,12]);
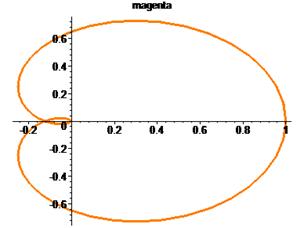
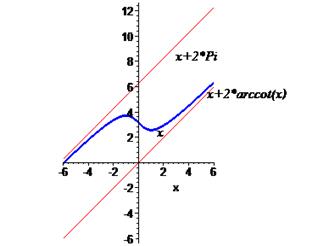
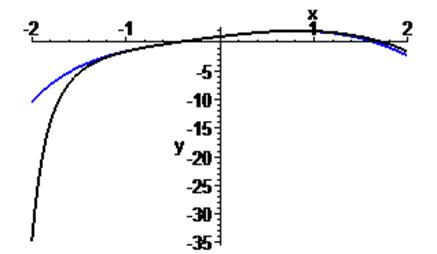
Построить график функции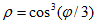 
в полярных координатах при 0 plot(cos(phi/3)^3,phi=0..4*Pi,color= magenta,thickness=3);
> with(plots):p:=plot([x+2*arccot(x), x, x+2*Pi], x=-6..6, color=[blue,red,red],thickness=[3,1,1], scaling=CONSTRAINED):tx1:=convert(x+2*arccot(x),string):t1:=textplot ([5.5,5.5,tx1], font=[TIMES,ITALIC,12], align=RIGHT):t2:=textplot ([1.5,2.5,»x»], font=[TIMES,ITALIC,12], align=RIGHT):tx3:=convert(x+2*Pi,string):t3:=textplot ([3,8.5,tx3], font=[TIMES,ITALIC,12], align=RIGHT):display([p,t1,t2,t3]);
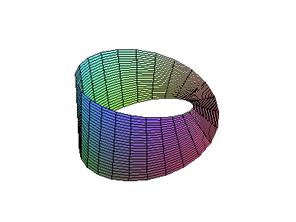
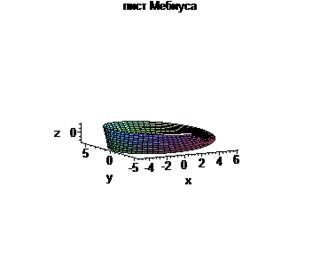
Нарисовать параметрически заданную поверхность (лист Мебиуса):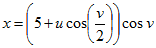 
, 
, 
, 
, 
.
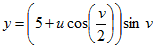
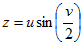
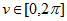
> restart;
> plot3d([((5+u*cos(v/2))*cos(v)), ((5+u*cos(v/2))*sin(v)), (u*sin(v/2))],v=0..2*Pi, u=-1..1);
Задайте изменение координат в интервалах 0 restart;
> plot3d([((5+u*cos(v/2))*cos(v)), ((5+u*cos(v/2))*sin(v)), (u*sin(v/2))],v=0..2*Pi, u=-1..1,title=»лист Мебиуса»,labels=[x,y,z],scaling=CONSTRAINED,grid=[60,10], orientation=[-106,70], axes=FRAMED, tickmarks=[5,8,3]);
Контрольные вопросы
Лабораторная работа №4
Лабораторная работа №5
Математический анализ: интегральное исчисление функции одной и многих переменных. Преобразование Лапласа.
1. Вычислить неопределенный интеграл 
.
> restart;
> Int((x^3-6)/(x^4+6*x^2+8),x)=
int((x^3-6)/(x^4+6*x^2+8),x);
Ответ:
2. Вычислить несобственный интеграл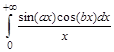 
при a>0 b>0 для случаев a>b, a=b, a restart;
> assume(a>0):assume(b>0):
> additionally(a>b):Int(sin(a*x)*cos(b*x)/x,x=0..+infinity)=int(sin(a*x)*cos(b*x)/x,x=0..+infinity);
Ответ: 
> restart;
> assume(a>0):assume(b>0):
> f:=sin(a*x)*cos(b*x)/x:
> additionally(a=b):Int(sin(a*x)*cos(b*x)/x,x=0..+infinity)=int(sin(a*x)*cos(b*x)/x,x=0..+infinity);
Ответ: 
> restart;
> assume(a>0):assume(b>0):
> f:=sin(a*x)*cos(b*x)/x:
> additionally(a restart;
> Int(sin(3*x)*exp(-1*x^2)/x^4, x=0.1..0.2)= evalf(int(sin(3*x)*exp(-1*x^2)/x^4, x=0.1..0.2));
Ответ:
4. Полностью проделать все этапы вычисления интеграла 
по частям
> restart;
> f:=x^3*cos(x);
> with(student):J:=Int(f,x=0..Pi/2);
> J:=intparts(Int(f,x=0..Pi/2),x^3);
> intparts(%,x^2);
> intparts(%,x);
> value(%);
Ответ:
5. Вычислить интеграл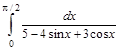 
с помощью универсальной подстановки tg(x/2)=t.
> restart;
> with(student):
> J=Int(1/(5-4*sin(x)+3*cos(x)), x=0..Pi/2);
> J=changevar(tan(x/2)=t,Int(1/(5-4*sin(x)+3*cos(x)), x=0..Pi/2),t);
> value(%);
Ответ: 
6. Вычислить тройной интеграл:
.
> restart: with(student):
> J:=Tripleint(ln(z-x-y)/((x-exp)*(x+y-exp)),x=exp..x+y+exp, y=0..exp-x-1, z=0..exp-1);
> value(%);
Ответ:
7.Найти изображения Лапласа и построить их графики для следующих функций:
а)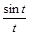 
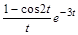
; б) 
.
> restart;
> with(inttrans):
> F(p):=laplace(sin(t)/t,t,p);
Ответ: 
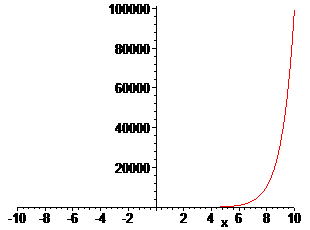
> plot(F(p),p);
> restart;
> with(inttrans):
> F(p):=laplace(((1-cos(2*t))*exp(-3*t))/t,t,p);
Ответ: 
> plot(F(p),p);
8. Найти оригинал Лапласа функции 
и построить его график.
> restart;
> with(inttrans):
> F(x):=invlaplace(1/(((p-1)^2)*(p^2+1)),p,x):
> combine(%,trig);
Ответ: 
> plot(F(x),x);
9.Дана функция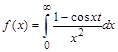 
, найти ее изображение Лапласа.
> restart;
> f(x):=int((1-cos(x*t))/x^2,x=0..+infinity);
> with(inttrans):
> F(p):=laplace(f(x),t,p);
> plot(F(p),p);
1. Что такое команды прямого и отложенного исполнения? Опишите их действия.
Ø Прямого исполнения – int(f, x), где f – подынтегральная функция, x – переменная интегрирования – вычисляет интеграл;
Ø Отложенного исполнения – Int(f, x) – где параметры команды такие же, как и в команде прямого исполнения int – выдает на экран интеграл в аналитическом виде математической формулы.
2. Какие команды производят аналитическое и численное интегрирование? Опишите их параметры.
int(f, x), где f – подынтегральная функция, x – переменная интегрирования (для вычисления определенного интеграла добавляются пределы интегрирования)
Если в команде интегрирования добавить опцию continuous: int(f, x, continuous), то Maple будет игнорировать любые возможные разрывы подынтегральной функции в диапазоне интегрирования.
Численное интегрирование выполняется командой evalf(int(f, x=x1..x2), e), где e – точность вычислений (число знаков после запятой).
3. С помощью каких команд вводятся ограничения на параметры для вычисления интегралов, зависящих от параметров?
Ограничения на параметры вводятся при помощи команды assume(expr1), где expr1 – неравенство. Дополнительные ограничения вводятся с помощью команды additionally(expr2), где expr2 – другое неравенство, ограничивающее значение параметра с другой стороны.
4. Для чего предназначен пакет student?
Пакет student, предназначенный для обучения математике. Он содержит набор подпрограмм, предназначенных для выполнения расчетов шаг за шагом, так, чтобы была понятна последовательность действий, приводящих к результату.
5. Опишите команду интегрирования по частям.
Если обозначить подынтегральную функцию f=u(x)v’(x), то параметры команды интегрирования по частям такие: intparts(Int(f, x), u),гдеu– именно та функция u(x), производную от которой предстоит вычислить по формуле интегрирования по частям.
6. Опишите команду интегрирования методом замены переменных.
Если в интеграле требуется сделать замену переменных x=g(t) или t=h(x), то параметры команды замены переменных такие: changevar(h(x)=t, Int(f, x), t),гдеt— новая переменная.
Эта команда, так же как и intparts не вычисляют окончательно интеграл, а лишь производят промежуточную выкладку.
7. Какие команды используются для вычисления двойных и тройных интегралов? Опишите их параметры.
В Maple имеются две специальные команды для вычисления двойных и тройных интегралов, содержащиеся в библиотеке student.
Для вычисления двойных интегралов используется команда Doubleint(f(x, y), D), где D – область интегрирования, записываемая в одном из следующих форматов:
§ x=х1..х2, y=y1..y2, где числа х1, х2, y1, y2задают прямоугольную область интегрирования;
Для вычисления тройных интегралов используется команда Tripleint(f(x, y, z),x, y, z, V), где V – область интегрирования.
Обе эти команды являются командами отложенного действия. Чтобы получить значение интеграла, следует использовать команду value(%).
Лабораторная работа №6
» Дифференциальные уравнения. Ряды»
Контрольные задания
> restart;
> Sum(1/(n*(n+1)*(n+2)), n=1..infinity)=sum(1/(n*(n+1)*(n+2)), n=1..infinity);
> s:=limit(rhs(S[N]), N=+infinity);
Ответ:
2.Разложить в степенной ряд f(x)=arcsinx в окрестности x=0 до 9-ого порядка.
> restart;
> f(x)=series((arcsin(x)), x=0, 9);
Ответ:
3.Разложить в ряд Тейлора функцию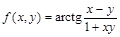 
до 6 – ого прядка в окрестности точки (0, 0).
> restart;
> readlib(mtaylor):
> f=mtaylor(arctan((x-y)/(1+x*y)),[x=0,y=0], 7);
> f = x-y-1/3*x^3+1/3*y^3+1/5*x^5-1/5*y^5;
Ответ:
4.Разложить в ряд Фурье функцию 
с периодом 4 на интервале [0;4], удерживая 6 членов ряда. Построить на одном рисунке графики функции и ее n-частичной суммы ряда Фурье.
> restart;
> fourierseries:=proc(f,x,x1,x2,n) local k, l,
a, b, s;
> l:=(x2-x1)/2;
> a[0]:=int(f,x=x1..x2)/l;
> a[k]:=int(f*cos(k*Pi*x/l),x=x1..x2)/l;
> b[k]:=int(f*sin(k*Pi*x/l),x=x1..x2)/l;
> s:=a[0]/2+sum(a[k]*cos(k*Pi*x/l)+
b[k]*sin(k*Pi*x/l), k=1..n);
> f:=piecewise(0 x1:=0:x2:=4:
> fr:=fourierseries(f,x,x1,x2,6);
> plot(
5. Найти общее решение дифференциального уравнения:
> restart;
> deq:=diff(y(x),x$2)-2*diff(y(x),x)-3*y(x)=x*exp(4*x)*sin(x);
> dsolve(deq,y(x));
6. Найти фундаментальную систему решений дифференциального уравнения:
> restart;
> de:=diff(y(x),x$3)+diff(y(x),x$2)=1-6*x^2*exp(-x);
> dsolve(de, y(x), output=basis);
Ответ:
7. Найти решение задачи Коши: y² –3y ¢+2y= 
> restart;
> de := diff(y(x),`$`(x,2))-3*diff(y(x),x)+2*y(x) = 1/(3+exp(-x));
> cond:=y(0)=1+8*ln(2), D(y)(0)=14*ln(2);
Ответ:
8. Найти решение системы дифференциальных уравнений:
> restart;
> sys:=diff(x(t),t$2)+5*diff(x(t),t)+2*diff(y(t),t)+y(t)=0,3*diff(x(t),t$2)+5*x(t)+diff(y(t),t)+3*y(t)=0:
> cond:=x(0)=1, D(x)(0)=0, y(0)=1;
Ответ:
9. Найти решение нелинейного уравнения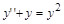 
при начальных условиях у(0)=2а, у‘(0)=а в виде разложения в степенной ряд до 6-го порядка.
> restart;
> Order:=6:
Ответ:
10. Построить график численного решения задачи Коши у‘=sin(xy), у(0)=1.
> restart;
> Ordev=6:
> eq:=diff(y(x),x)=sin(x*y(x)):
> cond:=y(0)=1:
> de:=dsolve(
> with(plots):
> odeplot(de,[x,y(x)],-10..10,thickness=2);
11. Решить численно задачу Коши: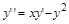 
, 
, 
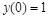
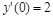
. Найти приближенное решение этого уравнения в виде разложения в степенной ряд. Построить на одном рисунке графики полученных решений.
> restart;
> Ordev=6:
> eq:=diff(y(x),x$2)=x*diff(y(x),x)-(y(x))^2:
> cond:=y(0)=1, D(y)(0)=2:
> de:=dsolve(
> de(0.5);
> dsolve(
> convert(%, polynom):p:=rhs(%):
> with(plots):
> p1:=odeplot(de,[x,y(x)],-2..2, thickness=2,color=black):
> p2:=plot(p,x=-2..2,thickness=2,linestyle=3,color=blue):
> display(p1,p2);
Ответ:
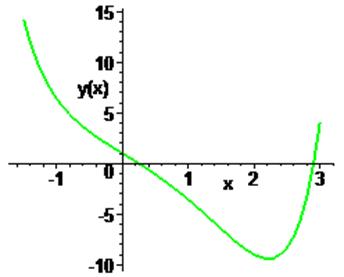
12. Построить график численного решения задачи Коши у»-xу‘+ xу=0, у(0)=1, у‘(0)=-4 на интервале [-1.5; 3], используя команду DEplot
> restart;
> with(DEtools):
> DEplot(diff(y(x),x$2)-x*diff(y(x),x)+x*y(x)=0,y(x),x=-1.5..3,[[y(0)=1,D(y)(0)=-4]],stepsize=.1,linecolor=green, thickness=2);
Контрольные вопросы
1. Какая команда позволяет решить дифференциальное уравнение? Опишите ее параметры.
Для нахождения аналитических решений дифференциальных уравнений в Maple применяется команда dsolve(eq,var,options), где eq – дифференциальное уравнение, var – неизвестные функции, options – параметры.
Параметры могут указывать метод решения задачи, например, по умолчанию ищется аналитическое решение: type=exact. При составлении дифференциальных уравнений для обозначения производной применяется команда diff.
2. С помощью каких операторов обозначается производная в дифференциальном уравнении и в начальных условиях?
При составлении дифференциальных уравнений для обозначения производной применяется команда diff.
Для обозначения производных в начальных или краевых условиях используется дифференциальный оператор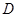 
.
3. Какой параметр команды dsolve следует установить, чтобы получить фундаментальную систему дифференциальных уравнений?
Команда dsolve предоставляет возможность найти фундаментальную систему решений дифференциального уравнения. Для этого в параметрах команды dsolve следует указать output=basis.
4. Какой параметр команды dsolve следует установить, чтобы получить приближенное решение дифференциального уравнения в виде разложения в степенной ряд? Как определяется порядок разложения?
Чтобы найти приближенное решение дифференциального уравнения в виде степенного ряда, в команде dsolve следует после переменных указать параметр type=series (или просто series). Для того, чтобы указать порядок разложения n, т.е. порядок степени, до которой производить разложение, следует перед командой dsolve вставить определение порядка с помощью команды Order:=n.
5. Опишите, какие команды нужно ввести, прежде чем построить график приближенного решения, полученного в виде степенного ряда.
Разложение в степенной ряд имеет тип series, поэтому для дальнейшей работы с этим рядом его следует преобразовать в полином с помощью команды convert(%,polynom), а затем выделить правую часть полученного выражения командой rhs(%).
6. Какой параметр команды dsolve следует установить, чтобы решить дифференциальное уравнение численно?
Для того, чтобы найти численное решение дифференциального уравнения (задачи Коши или краевой задачи) в команде dsolve следует указать параметр type=numeric (или просто numeric).
7. Как найти значение решения дифференциального уравнения в какой-либо конкретной точке?
Если необходимо получить значение решения при каком-то фиксированном значении переменной х (заодно будет выведено значение производной решения в этой точке), например, при х=0.5, то следует набрать:
> de(0.5);
8. Какая команда позволяет построить график численно решенного дифференциального уравнения?
График численного решения дифференциального уравнения можно построить с помощью команды odeplot(dd, [x,y(x)], x=x1..x2), где в качестве функции используется команда dd:=dsolve(
9. Какой пакет предназначен для графического представления и численного решения дифференциального уравнения?
Для численного решения задачи Коши, построения графиков решения и фазовых портретов в Maple имеется специальный пакет DEtools.
10. В чем отличие команд odeplot и DEplot?
Команда DEplot из пакета DEtools аналогична команде odeplot, но более функциональна. Она, в отличие от odeplot, сама производит численное решение дифференциального уравнения.
11. Как вычислить сумму или произведение в Maple?
Конечные и бесконечные суммы вычисляются командой прямого исполнения sum и отложенного исполнения Sum. Аргументы этих команд одинаковые: sum(expr, n=a..b), где expr – выражение, зависящее от индекса суммирования, a..b – пределы индекса суммирования, указывающие, что суммировать следует от n=a до n=b. Если требуется вычислить сумму бесконечного ряда, то в качестве верхнего предела вводится infinity.
Аналогичным образом вычисляются произведения командами прямого product(P(n),n=a..b) и отложенного действий Product P(n),n=a..b).
Лабораторная работа №7
Линейная алгебра
Контрольные задания
Задание № 1
Даны 2 вектора: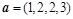 
, 
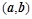
. Найти 
и угол j между этими векторами.
> with(linalg):
> dotprod(a,b);
> phi=angle(a,b);
Ответ:
Задание № 2
Даны 3 вектора: 
, 
и 
. Найти: 
и 
.
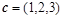
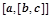
> restart; with(linalg):
> ab:=crossprod(a,b);
> x:=crossprod(ab,c);
> bc:=crossprod(b,c);
> f:=crossprod(a,bc);
Ответ: [[a,b],c]= 
[a,[b,c]]= 
Задание № 3
> restart;
> with(linalg):
> a1:=vector([2,1,3,-1]):
a2:=vector([7,4,3,-3]):
a3:=vector([1,1,-6,0]): a4:=vector([5,3,0,4]):
> g:=basis([a1,a2,a3,a4]);
> GramSchmidt(g);
Ответ:
Задание №4
Даны матрицы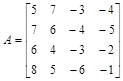 
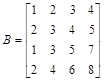
и 
. Найти: AB, BA, detA, debt
> restart;
> F:=evalm(A&*B);
> F:=evalm(B&*A);
> Det(A)=det(A); Det(B)=det(B);
Ответ: AB= 
BA= 
Задание № 5
> Det(A)=det(A);
> transpose(A);
> inverse(A);
> minor(A,3,2);
Ответ:
detA= 
M32=
A‘=
Задание № 6
Найти ранг матрицы: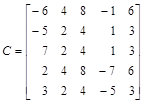 
. Привести матрицу С к треугольному виду.
> restart;
> C:=matrix([[-6,4,8,-1,6], [-5,2,4,1,3],
> gausselim(C);
Ответ:
Задание № 7
Дана матрица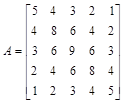 
. Найти ее спектр, характеристический многочлен и значение матрицы на нем (вместо переменной l в PА (l) подставить А).
> restart;
> with(linalg):
> A:=matrix([[5,4,3,2,1], [4,8,6,4,2], [3,6,9,6,3], [2,4,6,8,4],[1,2,3,4,5]]);
> eigenvalues(A);
> P(lambda):=charpoly(A,lambda);
> P(A):=evalm(A^5-35*A^4+336*A^3-1296*A^2+2160*A-1296);
Задание № 8
Дана матрица 
. Найти 
, det( ), собственные векторы и собственные числа матрицы , ядро матрицы Т.
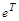
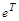
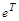
> with(linalg, exponential):
> exponential(Т);
>exp(T):=matrix([[1+3*exp(1),exp(1),3*exp(1)+1],[3*exp(1),3+exp(1),-3*exp(1)-3],[-1+3*exp(1),exp(1)+1,-3*exp(1)]]);
> det(exp(T));
> eigenvalues(exp(T));
> eigenvectors(exp(T));
> k(T):=kernel(T);
Ответ:
det( )=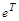
собственные числа матрицы =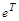
собственные векторы=
ядро матрицы Т=
Задание № 9
Дана матрица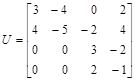 
. Найти нормальную форму Жордана, собственные векторы и числа, найти характеристический и минимальный многочлены.
> restart;
> with(linalg): A:=matrix([[3,4,0,2],[4,5,2,4],[0,0,3,2],[0,0,2,-1]]);