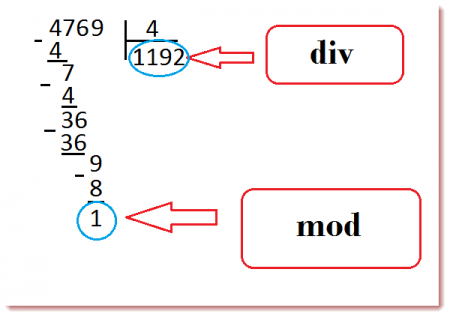
что такое mod в математике
Что такое mod в математике
Оператор div и оператор mod
В этой статье речь пойдет о целочисленном делении и делении с остатком.
То есть например 20 / 5 = 4, 55 / 6 = 9, 100 / 3 = 33 и т.д.
Согласитесь, что в некоторых случаях это очень удобно и практично. Теперь поговорим о реализации этого метода в Паскале. Тут все достаточно просто, открывать Америку не придется. В паскале за целочисленное деление отвечает оператор div. Теперь как это записывается в Pascal’e
Таким образом, вот такая запись (55 / 6) нацело = 9 в результате использования оператора div будет выглядеть так
z будет равно 9. Запомните! При использовании оператора div дробная часть будет отброшена!
А сейчас поговорим о делении с остатком. Оно не особо отличается и главным здесь является то, что в результате отбрасывается как раз целая часть. То есть (40 / 6) с остатком = 4, (10 / 3) с остатком =1, (22 /5) с остатком = 2 и т.д. В паскале для этого есть оператор mod. Записывается он точно так же.
Например (40 / 6) с остатком = 4 с оператором mod будет такой
Кстати оператор mod часто используют, для определения кратности чисел (кратность — это делимость на какое-нибудь число нацело. То есть например говорят, что числа 3, 6, 9, 12, 21 кратны трем. Или числа 5,10,15,20 кратны 5). В статье нахождение четных элементов массива я упоминал о числах кратных двум (четных). Итак как эту кратность определить в паскале. Обратите внимание, что если число кратное, то у него есть остаток (точнее оно имеет в остатке ноль). Этим и стоит воспользоваться.
Сейчас я привел пример условия, которое проверяет кратность, где v — это число, проверяемое на кратность по числу m. Например чтобы проверить,
является ли 40 кратным 4, используем оператор mod с условием и получим
[математикам]что такое mod?
в методичке по криптографии постоянно встречаются формулы вида этой:
Что такое mod? Простой остаток от деления e^-1 на p-1?
Судя по всему нет, т.к. вот пример из той же методички:
d = e^-1 (mod p-1) = 42239^-1 (mod(52631-1) = 32229
p.s. Да, математика в институте была >5 лет назад, и она вовсе не мой конек.
Re: [математикам]что такое mod?
а вроде всегда это был остаток от деления. число, не превосходящее делитель.
Re: [математикам]что такое mod?
//читаю лекции по криптографии у людей с большими провалами в математике, даже поля Галуа и теорему Ейлера можно объяснить на пальцах, ящитаю
Re: [математикам]что такое mod?
про (mod p-1) уже сказали, но
> d = e^-1 (mod p-1) = 42239^-1 (mod(52631-1) = 32229
либо очепятка, либо ошибка:
a^<-1>=b(mod c) если a*b=1(mod c), но у тут
Re: [математикам]что такое mod?
Re: [математикам]что такое mod?
Ужас. Закрывай методичку, открывай теорию чисел. А то что будет, когда дискретные логарифмы (ЕМНИП, ГОСТовское шифрование на них основано, но тут могу ошибаться, лет 10 криптографию не трогал) встретишь и т.д.
Re: [математикам]что такое mod?
ОМГ, так это ты подпускаешь людей без знания математики к криптографии?
Re: [математикам]что такое mod?
> //читаю лекции по криптографии у людей с большими провалами в математике, даже поля Галуа и теорему Ейлера можно объяснить на пальцах, ящитаю
Объясните на пальцах БПФ. Не что он делает, а КАК.
Ну мля, я хочу понять, как всё-таки эти формулы с интегралами в циклы расписать чтобы ему на вход массив с PCM, на выходе массив с частотами.
Re: [математикам]что такое mod?
Здесь либо порядок операций нужно смотреть, либо ограничение представления машинного числа в памяти компа. Положительное integer принимает значения от 0 до 32767. Ну, типа тогда 0-1=32767.
Re: [математикам]что такое mod?
Ну что такое остаток я понимаю, но как его найти в данном примере? Ведь e^ <-1>явно меньше чем (p-1)?
p.s. эта формула из «трехподходного протокола Шамира»
Re: [математикам]что такое mod?
Самое простое объяснение: в методичке опечатка, пропущена какая-то буква перед «-1».
Re: [математикам]что такое mod?
Re: [математикам]что такое mod?
Это таки точно опечатка. У меня получается 34229, что слишком похоже на 32229, чтобы быть случайным.
Re: [математикам]что такое mod?
Т.е. получается: d = e^ <-1>(mod p-1) = 42239^ <-1>(mod(52631-1) = 34229
Еще раз, для малограмотных, объясните как взять остаток от деления 42239^ <-1>= 2.36748029073e-05 на 52630?
Re: [математикам]что такое mod?
>как взять остаток от деления 42239^
Re: [математикам]что такое mod?
Спасибо, тогда тоже пока напишу скрипт, пусть ищет.
Оператор mod — остаток от деления. Что такое mod?
Оператор mod обозначается символом % и является оператором деления по модулю. Он возвращает остаток от деления 1-го операнда на 2-й и широко используется в разных языках программирования для решения ряда задач.
Оператор mod в Java
В Java operator mod может работать как с целыми числами (byte/int/short/long), так и с плавающей точкой (byte/int/short/long). Давайте приведём пример работы оператора mod при делении:
После выполнения этой программы вы получите результат следующего вида:
Как видим, оператор mod — это прекрасный способ найти остаток от деления. Зачем это может понадобиться на практике? Например, при нахождении кратности числа и определении, является ли некоторое число, введённое с клавиатуры, чётным. Также с помощью оператора mod можно узнать, делится ли одно число на другое без остатка или определить последнюю цифру числа. В общем, оператор mod очень полезен при решении различных задач по программированию.
Оператор mod в SQL
Не менее интересно использование mod в базах данных. Аналогично, mod находит остаток от деления. При этом вместо mod можно задействовать операцию %, делающую то же самое. Синтаксис в SQL следующий:
Но можно написать и иначе, используя % :
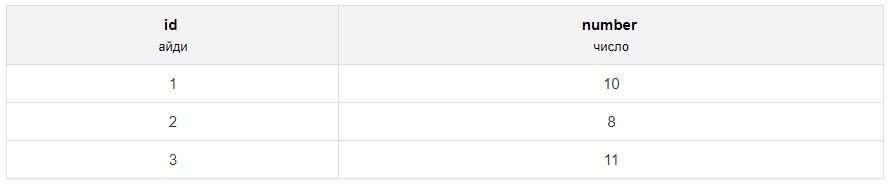
Давайте приведём пример использования mod в базах данных. Вот, например, таблица numbers:
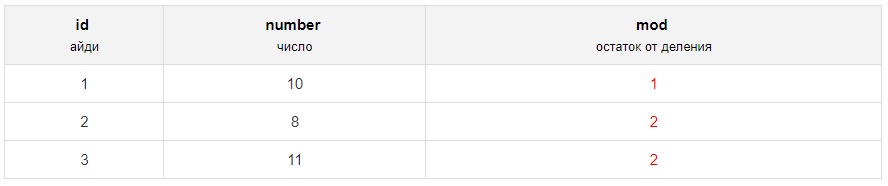
Найдём остаток от деления столбца number на три:
В результате запрос SQL выберет следующие строки:
Но, как мы уже говорили выше, этот же запрос можно без проблем переписать:
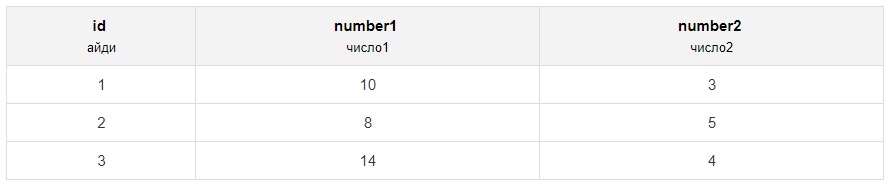
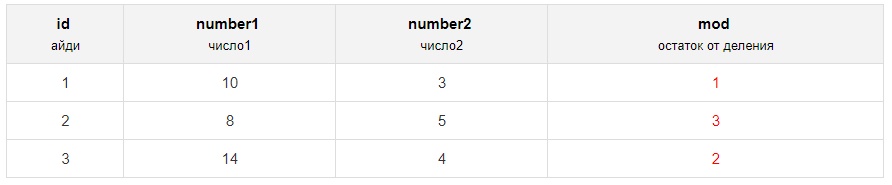
Идём дальше. Теперь возьмём таблицу посложнее:
Здесь найдём остаток от деления столбца number1 на number2:
Получим следующие строки:
Опять же, этот же самый запрос можно оформить иначе:
А где вы используете mod? Пишите в комментариях!
Деление чисел с остатком
Деление с остатком целых положительных чисел
Деление — это разбиение целого на равные части.
Остаток от деления — это число, которое образуется при делении с остатком. То есть то, что «влезло» и осталось, как хвостик.
Чтобы научиться делить числа с остатком, нужно усвоить некоторые правила. Начнем!
Все целые положительные числа являются натуральными. Поэтому деление целых чисел выполняется по всем правилам деления с остатком натуральных чисел.
Попрактикуемся в решении.
Пример
Разделить 14671 на 54.
Выполним деление столбиком:
Неполное частное равно 271, остаток — 37.
Ответ: 14671 : 54 = 271(остаток 37).
Деление с остатком положительного числа на целое отрицательное
Чтобы легко выполнить деление с остатком положительного числа на целое отрицательное, обратимся к правилу:
В результате деления целого положительного a на целое отрицательное b получаем число, которое противоположно результату от деления модулей чисел a на b. Тогда остаток равен остатку при делении |a| на |b|.
Неполное частное — это результат деления с остатком. Обычно в ответе записывают целое число и рядом остаток в скобках.
Это правило можно описать проще: делим два числа со знаком «плюс», а после подставляем «минус».
Все это значит, что «хвостик», который у нас остается, когда делим положительное число на отрицательное — всегда положительное число.
Алгоритм деления положительного числа на целое отрицательное (с остатком):
Пример
Разделить 17 на −5 с остатком.
Применим алгоритм деления с остатком целого положительного числа на целое отрицательное.
Разделим 17 на − 5 по модулю. Отсюда получим, что неполное частное равно 3, а остаток равен 2. Получим, что искомое число от деления 17 на − 5 = − 3 с остатком 2.
Ответ: 17 : (− 5) = −3 (остаток 2).
Деление с остатком целого отрицательного числа на целое положительное
Чтобы быстро разделить с остатком целое отрицательное число на целое положительное, тоже придумали правило:
Чтобы получить неполное частное с при делении целого отрицательного a на положительное b, нужно применить противоположное данному числу и вычесть из него 1. Тогда остаток d будет вычисляться по формуле:
d = a − b * c
Из правила делаем вывод, что при делении получается целое неотрицательное число.
Для точности решения применим алгоритм деления а на b с остатком:
Рассмотрим пример, где можно применить алгоритм.
Пример
Найти неполное частное и остаток от деления −17 на 5.
Разделим заданные числа по модулю.
Получаем, что при делении частное равно 3, а остаток 2.
Так как получили 3, противоположное ему −3.
Необходимо отнять единицу: −3 − 1 = −4.
Чтобы вычислить остаток, необходимо a = −17, b = 5, c = −4, тогда:
d = a − b * c = −17 − 5 * (−4) = −17 − (− 20) = −17 + 20 = 3.
Значит, неполным частным от деления является число −4 с остатком 3.
Ответ: (−17) : 5 = −4 (остаток 3).
Деление с остатком целых отрицательных чисел
Сформулируем правило деления с остатком целых отрицательных чисел:
Для получения неполного частного с от деления целого отрицательного числа a на целое отрицательное b, нужно произвести вычисления по модулю, после чего прибавить 1. Тогда можно произвести вычисления по формуле:
d = a − b * c
Из правила следует, что неполное частное от деления целых отрицательных чисел — положительное число.
Алгоритм деления с остатком целых отрицательных чисел:
Пример
Найти неполное частное и остаток при делении −17 на −5.
Применим алгоритм для деления с остатком.
Разделим числа по модулю. Получим, что неполное частное равно 3, а остаток равен 2.
Сложим неполное частное и 1: 3 + 1 = 4. Из этого следует, что неполное частное от деления заданных чисел равно 4.
Для вычисления остатка применим формулу. По условию a = −17, b = −5, c = 4, тогда получим d = a − b * c = −17 − (−5) * 4 = −17 − (−20) = −17 + 20 = 3.
Получилось, что остаток равен 3, а неполное частное равно 4.
Ответ: (−17) : (−5) = 4 (остаток 3).
Деление с остатком с помощью числового луча
Деление с остатком можно выполнить и на числовом луче.
Пример 1
Рассмотрим выражение: 10 : 3.
Отметим на числовом луче отрезки по 3 деления. Видим, что три деления помещаются полностью три раза и одно деление осталось.
Решение: 10 : 3 = 3 (остаток 1).
Пример 2
Рассмотрим выражение: 11 : 3.
Отметим на числовом луче отрезки по 3 деления. Видим, что три деления поместились три раза и два деления осталось.
Решение: 11 : 3 = 3 (остаток 2).
Проверка деления с остатком
Пока решаешь пример, бывает всякое: то в окно отвлекся, то друг позвонил. Чтобы убедиться в том, что все правильно, важно себя проверять. Особенно ученикам 5 класса, которые только начали проходить эту тему.
Формула деления с остатком
a = b * c + d,
где a — делимое, b — делитель, c — неполное частное, d — остаток.
Эту формулу можно использовать для проверки деления с остатком.
Пример
Рассмотрим выражение: 15 : 2 = 7 (остаток 1).
В этом выражении: 15 — это делимое, 2 — делитель, 7 — неполное частное, а 1 — остаток.
Чтобы убедиться в правильности ответа, нужно неполное частное умножить на делитель (или наоборот) и к полученному произведению прибавить остаток. Если в результате получится число, которое равно делимому, то деление с остатком выполнено верно. Вот так:
Теорема о делимости целых чисел с остатком
Если нам известно, что а — это делимое, тогда b — это делитель, с — неполное частное, d — остаток. И они между собой связаны. Эту связь можно описать через теорему о делимости с остатком и показать при помощи равенства.
Теорема
Любое целое число может быть представлено только через целое и отличное от нуля число b таким образом:
где q и r — это некоторые целые числа. При этом 0 ≤ r ≤ b.
Доказательство:
Если существуют два числа a и b, причем a делится на b без остатка, тогда из определения следует, что есть число q, и будет верно равенство a = b * q. Тогда равенство можно считать верным: a = b * q + r при r = 0.
Тогда необходимо взять q такое, чтобы данное неравенством b * q
Учебник. Сравнения по модулю и признаки делимости
Два натуральных числа a и b, разность которых кратна натуральному числу m, называются сравнимыми по модулю m: a ≡ b (mod m).
Так, 3 ≡ 1 (mod 2), 7 ≡ 1 (mod 3). Два числа сравнимы по модулю 2, если они оба четны, либо если они оба нечетны. По модулю 1 все целые числа сравнимы между собой.
В том случае, если число n делится на m, то оно сравнимо с нулем по модулю m: n ≡ 0 (mod m).
Свойства сравнений по модулю вытекают из свойств арифметических операций.
Отметим, что обе части сравнения не всегда можно сократить на какой-либо множитель. Так, 6 ≡ 3 (mod 3), но 2 не сравнимо с 1 по этому же модулю.
Простейшим применением сравнений по модулю является определение делимости чисел. Дадим для начала несколько правил.
Признак делимости на 2. Число, делящееся на 2, называется чётным, не делящееся на 2 – нечётным. Число делится на 2 тогда и только тогда, когда его последняя цифра делится на 2.
Признак делимости на 5. Число делится на 5 тогда и только тогда, когда его последняя цифра – 5 или 0.
Признак делимости на 25. Число делится на 25 тогда и только тогда, когда две его последние цифры либо нули, либо образуют число, делящееся на 25.
Признаки делимости на 10, 100, 1000. Число делится на 10 тогда и только тогда, когда его последняя цифра – 0. Число делится на 100 тогда и только тогда, когда две его последние цифры – нули. Число делится на 1000 тогда и только тогда, когда три его последние цифры – нули.
Признак делимости на 4. Число делится на 4 тогда и только тогда, когда две его последние цифры – нули, либо когда двузначное число, образованное двумя его последними цифрами, делится на 4.
Признак делимости на 3. Число делится на 3 тогда и только тогда, когда сумма его цифр делится на 3.
Признак делимости на 9. Число делится на 9 тогда и только тогда, когда сумма его цифр делится на 9.
Признак делимости на 11. Число делится на 11 тогда и только тогда, когда сумма его цифр, стоящих на нечётных местах, либо равна сумме цифр, стоящих на чётных местах, либо отличается от неё на число, кратное 11.
Доказать свойство делимости на 9: число делится на 9 тогда и только тогда, когда сумма всех его цифр делится на 9.
Доказать, что число делится без остатка на 19 тогда и только тогда, когда число его десятков, сложенное с удвоенным числом единиц, кратно 19.
Для любого натурального x верно равенство x = x1 + 10x2, где x1 – число единиц, x2 – число десятков этого числа. Пусть y = x2 + 2x1 (то есть y – число десятков, сложенное с удвоенным числом единиц). Тогда 10y – x = 19x1 ≡ 0 (mod 19), откуда следует, что x ≡ 0 (mod 19) тогда и только тогда, когда 10y ≡ 0 (mod 19), то есть y ≡ 0 (mod 19). Утверждение доказано.
В заключение этого параграфа приведем формулировку малой теоремы Ферма.
Пусть p – простое число, a – натуральное число. Тогда a p – a делится на p: a p ≡ a (mod p).
В частности, если p – простое число, a – натуральное число, взаимно простое с p, то a p – 1 ≡ 1 (mod p).
Запишите состоящее из одних девяток натуральное число, которое делится на 17 без остатка.
Воспользуемся малой теоремой Ферма: a p – 1 ≡ 1 (mod p). Положим a = 10, p = 17. Тогда 10 16 ≡ 1 (mod 17) или 10 16 – 1 ≡ 0 (mod 17). Число 10 16 – 1 состоит из 16 девяток. Это и есть одно из чисел, которые делятся на 17 без остатка.