что такое res в математике
Комплексные числа
Формы
Так сложилось в математике, что у данных чисел несколько форм. Число одно и тоже, но записать его можно по-разному:
Далее с примерами решений вы узнаете как переводить комплексные числа из одной формы в другую путем несложных действий в обе стороны.
Изображение
Изучение выше мы начали с алгебраической формы. Так как она является основополагающей. Чтобы было понятно в этой же форме изобразим комплексное число на плоскости:
Вычислить сумму и разность заданных комплексных чисел:
Сначала выполним сложение. Для этого просуммируем соответствующие мнимые и вещественные части комплексных чисел:
Аналогично выполним вычитание чисел:
Выполнить умножение и деление комплексных чисел:
Так, теперь разделим первое число на второе:
Суть деления в том, чтобы избавиться от комплексного числа в знаменателе. Для этого нужно домножить числитель и знаменатель дроби на комплексно-сопряженное число к знаменателю и затем раскрываем все скобки:
Разделим числитель на 29, чтобы записать дробь в виде алгебраической формы:
Для возведения в квадрат достаточно умножить число само на себя:
Пользуемся формулой для умножения, раскрываем скобки и приводим подобные:
В этом случае не всё так просто как в предыдущем случае, когда было возведение в квадрат. Конечно, можно прибегнуть к способу озвученному ранее и умножить число само на себя 7 раз, но это будет очень долгое и длинное решение. Гораздо проще будет воспользоваться формулой Муавра. Но она работает с числами в тригонометрической форме, а число задано в алгебраической. Значит, прежде переведем из одной формы в другую.
Вычисляем значение модуля:
Найдем чем равен аргумент:
$$ \varphi = arctg \frac<3> <3>= arctg(1) = \frac<\pi> <4>$$
Записываем в тригонометрическом виде:
Преобразуем в алгебраическую форму для наглядности:
Представим число в тригонометрической форме. Найдем модуль и аргумент:
Используем знакомую формулу Муавра для вычисления корней любой степени:
Что такое комплексное число? Примеры
Тема «Комплексные числа» зачастую вызывает затруднения у учащихся, а ведь на самом деле в них нет ничего страшного, как может показаться на первый взгляд.
Итак, сейчас мы разберем и рассмотрим на простых примерах, что такое комплексное число, как обозначается и из чего состоит. Выражение z = a + bi называется комплексным числом. Это единое число, а не сложение.
Пример 1: z = 6 + 4i
Из чего состоит комплексное число?
Комплексное число имеет действительную и мнимую часть в своем составе.
Число a называется действительной частью комплексного числа и обозначается a = Re (z). А вот то, что стоит вместе с буквой i — т.е. число b называется коэффициентом мнимой части комплексного числа и обозначается b = Im (z). Вместе bi образуют мнимую часть комплексного числа.
Нетрудно догадаться и легко запомнить, что сокращение «Re» происходит от слова «Real» — реальная, действительная часть. Соответственно, «Im» является сокращением слова «Imaginary» — мнимая, воображаемая часть.
Пример 2: z = 0,5 + 9i. Здесь действительная часть a = Re (z) = 0,5, а мнимая часть b = Im (z) = 9i
Чисто мнимое комплексное число
Комплексное число, в котором нет действительной части, т.е. Re (z) = 0, называется чисто мнимым.
Пример 4: z = 2i. Действительная часть отсутствует, a = Re (z) = 0, а мнимая часть b = Im (z) = 2.
Сопряженные комплексные числа
Комплексно-сопряженное число обозначается «зэт» с чертой и используется, к примеру, для нахождения частного двух комплексных чисел, проще говоря — для реализации деления чисел. Те, кто сейчас задумался, вам сюда — читать про деление комплексных чисел.
Числа называются комплексно-сопряженными, имеют одинаковые действительные части и различаются лишь знаком мнимых частей. Рассмотрим пример:
Мнимая единица комплексного числа
И наконец поговорим про букву i. Та самая буква, которая образует в комплексном числе мнимую составляющую. Даже если перед нами выражение z = 5, это просто значит, что мнимая часть данного числа равна нулю, а действительная равна пяти.
Величина i называется мнимой единицей.
Мнимая единица пригодится при решении квадратных уравнений в случае, когда дискриминант меньше нуля. Мы привыкли считать, что если он отрицательный, решения нет, корней нет. Это не совсем корректно. Корни существуют, просто они комплексные. Но об этом позже. А теперь, переходим к следующей статье по изучению комплексных чисел, узнаем же, как посчитать произведение комплексных чисел.
Что такое res в математике
где x и y – действительные числа, а i так называемая мнимая единица. Соотношение для мнимой единицы
Понятия «больше» и «меньше» для комплексных чисел не вводятся.
Числа z = x + iy и 
называются комплексно сопряженными.
Алгебраической формой комплексного числа называется з апись числа z в виде z = x + iy.
Модуль r и аргумент φ можно рассматривать как полярные координаты вектора 
, изображающего комплексное число z = x + iy (см. рис. 7.1). Тогда из соотношений сторон в прямоугольном треугольнике получаем
Равенство (7.3) есть тригонометрическая форма комплексного числа. Модуль r = |z| однозначно определяется по формуле
Аргумент определяется из формул:
Используя формулу Эйлера
комплексное число 
можно записать в так называемой показательной (или экспоненциальной) форме
где r =| z | — модуль комплексного числа, а угол 
( k =0;–1;1;–2;2…).
Пример 7.1. Записать комплексные числа 
в тригонометрической и показательной формах.
На множестве комплексны х чисел определен ряд операций.
Из (7.11) следует важнейшее соотношение i 2 = –1. Действительно,
Видно, что при умножении комплексных чисел в тригонометрической форме их модули перемножаются, а аргументы складываются. Это правило распространяется на любое конечное число множителей. Нетрудно видеть, что если есть n множителей и все они одинаковые, то частным случаем равенства (7.12) является формула возведения комплексного числа в натуральную степень:
(7.13) называется первой формулой Муавра.
Произведение двух комплексных чисел в показательной (экспоненциальной) форме имеет вид:
На практике при нахождении частного двух комплексных чисел удобно умножить числитель и знаменатель дроби 
на число, сопряженное знаменателю, с дальнейшим применением равенства i 2 = –1 и формулы разности квадратов.
Деление комплексных чисел осуществляется также и в тригонометрической форме, при этом имеет место формула:
Видно, что при делении комплексных чисел их модули делятся, а аргументы вычитаются соответственно.
Частное двух комплексных чисел в показательной (экспоненциальной) форме имеет вид:
Пользуясь формулой (7.11), вычислим их произведение
На основании формулы (7.14) вычислим их частное
Решение. Используя (7.4) и (7.5), получаем:
Аналогично, для z 2 можно записать:
По формулам (7.12) и (7.16) получим в тригонометрической форме:
Пользуясь формулами (7.14) и (7.17), получим в показательной форме:
в натуральную степень, определенному ранее формулой (7.13).
(7.18) называется второй формулой Муавра.
Пример 7.4. Найти все корни уравнения z 4 +16=0.
Теорема 7.1 (основная теорема алгебры). Для всякого многочлена с комплексными коэффициентами
Приведем еще одну теорему, имеющую место над множеством комплексных чисел.
Таким образом, произведение линейных множителей, соответствующих сопряженным корням, можно заменить квадратным трехчленом с действительными коэффициентами, а соответствующее квадратное уравнение будет иметь отрицательный дискриминант.
Иллюстрированный самоучитель по Mathematica 5
Комплексные числа
Мнимая единица
На специальной панели символов системы Mathematica имеется мнимая единица, но иногда ее удобно ввести просто как букву I или даже как \[Imaginaryi] или \[ImaginaryJ]. Вот примеры.
Вещественная часть комплексного числа: функция Re
Это совсем незамысловатая функция, возвращающая вещественную часть комплексного числа.
Заметьте, что в последнем примере вещественность а и b не предполагается.
Мнимая часть комплексного числа: функция Im
Тоже совсем незамысловатая функция, возвращающая мнимую часть комплексного числа.
Заметьте, что в случае Im[a+b I] вещественность а и b не предполагается – в отличие от случая, когда используется функция ComplexExpand.
Аргумент комплексного числа: функция Arg
Функция Arg[z] возвращает аргумент комплексного числа z.
Вот как, например, можно получить аргументы корней четвертой степени из 1.
Возвращаемый угол всегда по абсолютной величине не превосходит n.
Сопряженное комплексное число: функция Conjugate
Выражение Conjugate [z] представляет собой сопряженное комплексное число z. Вот как, например, можно получить число, сопряженное к х+I у.
Заметьте, что х и у предполагаются комплексными.
Резюме
Мы рассмотрели основные числовые системы, предусмотренные в системе Mathematica. Они полностью охватывают классическую математику. Благодаря такому богатству система Mathematica может помочь в решении практически любых математических задач. Но благодаря этому же богатству при решении задач можно столкнуться с теми же проблемами, что и в математике. И потому решение исследовательских задач с помощью системы Mathematica может потребовать основательного знакомства с методологией применения данной системы в конкретной области науки и техники. Конечно, по высказыванию Гаусса, математика – царица всех наук. И потому в первую очередь следует освоить именно методологию применения системы Mathematica к решению математических задач. И начнем мы с царицы математики (по выражению того же Гаусса) – с арифметики.
Электронная библиотека
Действительные числа x и y называются соответственно действительной и мнимой частью комплексного числа z и обозначаются:
Множество комплексных чисел обозначают буквой С.
Например, – комплексное число, где Rez = 5 – действительная часть; Imz = 8 – мнимая часть.
Пример 1
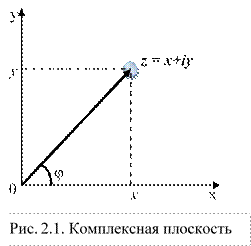
Таким образом, между множеством C и множеством векторов (и точек!) плоскости xOy устанавливается взаимно однозначное соответствие.
Определения. Плоскость xОy называется плоскостью комплексных чисел (или просто комплексной плоскостью), будем её обозначать Z. Ось Ox – действительная ось; ось Oy – мнимая ось.
Поскольку – вектор, то он имеет длину и характеризуется направлением.
Длину вектора называют модулем комплексного числа z = х + iy, а величину угла наклона вектора по отношению к оси Ox – аргументом z. Их обозначают символами:
Модуль комплексного числа есть однозначная функция:
Из рисунка 2.1 видно, что:
Аргумент есть функция многозначная. Все значения аргумента удовлетворяют соотношению:
Из формул (2.5) и (2.6) следует:
Пример 2
Необходимо: найти модуль комплексного числа, изобразить число на комплексной плоскости, найти главное значение аргумента комплексного числа.
Используем формулу (*) и находим модуль комплексного числа:
Изобразим число на комплексной плоскости (рис. 2.2).
Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00