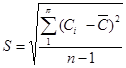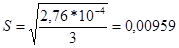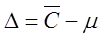что такое rsd в статистике
Стандартное отклонение
Стандартное отклонение (англ. Standard Deviation) — простыми словами это мера того, насколько разбросан набор данных.
Вычисляя его, можно узнать, являются ли числа близкими к среднему значению или далеки от него. Если точки данных находятся далеко от среднего значения, то в наборе данных имеется большое отклонение; таким образом, чем больше разброс данных, тем выше стандартное отклонение.
Стандартное отклонение обозначается буквой σ (греческая буква сигма).
Стандартное отклонение также называется:
Использование и интерпретация величины среднеквадратического отклонения
Стандартное отклонение используется:
Рассмотрим два малых предприятия, у нас есть данные о запасе какого-то товара на их складах.
| День 1 | День 2 | День 3 | День 4 | |
|---|---|---|---|---|
| Пред.А | 19 | 21 | 19 | 21 |
| Пред.Б | 15 | 26 | 15 | 24 |
В обеих компаниях среднее количество товара составляет 20 единиц:
Однако, глядя на цифры, можно заметить:
Если рассчитать стандартное отклонение каждой компании, оно покажет, что
Стандартное отклонение показывает эту волатильность данных — то, с каким размахом они меняются; т.е. как сильно этот запас товара на складах компаний колеблется (поднимается и опускается).
Расчет среднеквадратичного (стандартного) отклонения
Формулы вычисления стандартного отклонения
Разница между формулами S и σ («n» и «n–1»)
Состоит в том, что мы анализируем — всю выборку или только её часть:
Как рассчитать стандартное отклонение?
Пример 1 (с σ)
Рассмотрим данные о запасе какого-то товара на складах Предприятия Б.
| День 1 | День 2 | День 3 | День 4 | |
| Пред.Б | 15 | 26 | 15 | 24 |
Если значений выборки немного (небольшое n, здесь он равен 4) и анализируются все значения, то применяется эта формула:
Применяем эти шаги:
1. Найти среднее арифметическое выборки:
μ = (15 + 26 + 15+ 24) / 4 = 20
2. От каждого значения выборки отнять среднее арифметическое:
3. Каждую полученную разницу возвести в квадрат:
4. Сделать сумму полученных значений:
5. Поделить на размер выборки (т.е. на n):
6. Найти квадратный корень:
Пример 2 (с S)
Задача усложняется, когда существуют сотни, тысячи или даже миллионы данных. В этом случае берётся только часть этих данных и анализируется методом выборки.
У Андрея 20 яблонь, но он посчитал яблоки только на 6 из них.
Популяция — это все 20 яблонь, а выборка — 6 яблонь, это деревья, которые Андрей посчитал.
| Яблоня 1 | Яблоня 2 | Яблоня 3 | Яблоня 4 | Яблоня 5 | Яблоня 6 |
| 9 | 2 | 5 | 4 | 12 | 7 |
Так как мы используем только выборку в качестве оценки всей популяции, то нужно применить эту формулу:
Математически она отличается от предыдущей формулы только тем, что от n нужно будет вычесть 1. Формально нужно будет также вместо μ (среднее арифметическое) написать X ср.
Применяем практически те же шаги:
1. Найти среднее арифметическое выборки:
Xср = (9 + 2 + 5 + 4 + 12 + 7) / 6 = 39 / 6 = 6,5
2. От каждого значения выборки отнять среднее арифметическое:
X1 – Xср = 9 – 6,5 = 2,5
X2 – Xср = 2 – 6,5 = –4,5
X3 – Xср = 5 – 6,5 = –1,5
X4 – Xср = 4 – 6,5 = –2,5
X5 – Xср = 12 – 6,5 = 5,5
X6 – Xср = 7 – 6,5 = 0,5
3. Каждую полученную разницу возвести в квадрат:
4. Сделать сумму полученных значений:
Σ (Xi – Xср)² = 6,25 + 20,25+ 2,25+ 6,25 + 30,25 + 0,25 = 65,5
5. Поделить на размер выборки, вычитав перед этим 1 (т.е. на n–1):
(Σ (Xi – Xср)²)/(n-1) = 65,5 / (6 – 1) = 13,1
6. Найти квадратный корень:
S = √((Σ (Xi – Xср)²)/(n–1)) = √ 13,1 ≈ 3,6193
Дисперсия и стандартное отклонение
Стандартное отклонение равно квадратному корню из дисперсии (S = √D). То есть, если у вас уже есть стандартное отклонение и нужно рассчитать дисперсию, нужно лишь возвести стандартное отклонение в квадрат (S² = D).
Дисперсия — в статистике это «среднее квадратов отклонений от среднего». Чтобы её вычислить нужно:
Ещё расчёт дисперсии можно сделать по этой формуле:
Правило трёх сигм
Это правило гласит: вероятность того, что случайная величина отклонится от своего математического ожидания более чем на три стандартных отклонения (на три сигмы), почти равна нулю.
Глядя на рисунок нормального распределения случайной величины, можно понять, что в пределах:
Это означает, что за пределами остаются лишь 0,28% — это вероятность того, что случайная величина примет значение, которое отклоняется от среднего более чем на 3 сигмы.
Стандартное отклонение в excel
Вычисление стандартного отклонения с «n – 1» в знаменателе (случай выборки из генеральной совокупности):
1. Занесите все данные в документ Excel.
2. Выберите поле, в котором вы хотите отобразить результат.
3. Введите в этом поле «=СТАНДОТКЛОНА(«
4. Выделите поля, где находятся данные, потом закройте скобки.
5. Нажмите Ввод (Enter).
В случае если данные представляют всю генеральную совокупность (n в знаменателе), то нужно использовать функцию СТАНДОТКЛОНПА.
Коэффициент вариации
Коэффициент вариации — отношение стандартного отклонения к среднему значению, т.е. Cv = (S/μ) × 100% или V = (σ/X̅) × 100%.
Стандартное отклонение делится на среднее и умножается на 100%.
Можно классифицировать вариабельность выборки по коэффициенту вариации:
Случайные погрешности (e)



Погрешности, причиной которых являются случайные, неконтролируемые изменения условий измерения, называются случайными погрешностями. Так как на условия измерения действует множество различных факторов, причины возникновения случайных погрешностей не всегда известны и часто непредсказуемы. Действие этих факторов приводит к тому, что отклонение результата измерения от истинного значения концентрации носит статистический, вероятностный характер.
При параллельных измерениях величина случайных погрешностей изменяется случайным образом. Какова будет погрешность каждого единичного измерения предсказать нельзя. Но можно оценить наиболее вероятную максимальную случайную погрешность методики анализа.
На практике при выполнении анализа по стандартизованной методике получают ограниченное число результатов. Совокупность ограниченного числа результатов измерений называют выборкой, а их количество — объемом выборки. Мерой случайной погрешности в этом случае является стандартное отклонение небольшого объема выборки S, которое часто называют среднеквадратичным отклонением (СКО)
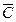
При определении концентрации хрома в стальном образце атомно-эмиссионным методом анализа выполнили четыре параллельных измерения и получили данные (Cr %): 1,44; 1,45; 1,43; 1,45. Рассчитаем стандартно отклонение малой выборки по формуле 4.5
а) 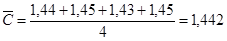
График, отражающий зависимость количества измерений с данной случайной погрешностью от величины этой погрешности, называется кривой распределения случайных погрешностей.
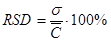
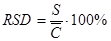
По данной методике анализируют стандартный образец (сравнение по паспорту с найдено конц-ии).
Чаще всего численная величина систематической погрешности остается неизменной при параллельных измерениях и не зависит от концентрации, такие погрешности называют постоянными.
Систематические погрешности бывают положительными и отрицательными.
Систематическая погрешность — аддитивна, т.е. общая систематическая погрешность результата анализа равна сумме систематических погрешностей, возникающих на всех этапах в ходе анализа.
Систематическая погрешность в процессе выполнения количественного анализа не видна.
причиной систематической погрешности является недостаточное соответствие химического и минералогического состава стандартных образцов с составом анализируемых образцов.
В статистике RSD обозначает относительное стандартное отклонение и также известен как коэффициент дисперсии. RSD измеряет точность усреднения ваших результатов. Он может быть представлен в процентах или в виде основной цифры и может быть добавлен или вычтен из вашего основного измерения. Например, стандартное отклонение в 6%, если ваш средний результат равен 40, будет означать, что подавляющее большинство результатов находится в диапазоне от 34 до 46. Ваш результат будет иметь значение 40 +/- 6%. Чем меньше рассчитанное относительное стандартное отклонение, тем точнее измерение. Он часто используется в химии, и его довольно просто рассчитать.
Найдите свое стандартное отклонение. См. Предлагаемые ниже ресурсы для получения подробных инструкций по поиску стандартного отклонения.
Найдите свое среднее значение, сложив все свои результаты и разделив его на количество результатов, которые вы получили.
Возьмите стандартное отклонение и умножьте его на 100.
Разделите число, полученное на шаге 2, на среднее значение.
Используя эту формулу, если у вас есть стандартное отклонение 2 и среднее значение 100, это будет выглядеть так: (2 * 100) / 100, 200/100 = 2. Ваше относительное стандартное отклонение составляет 2%.
Как рассчитать, как долго будет работать 9-вольтовая батарея
Как рассчитать щелочность как концентрацию caco3
Щелочность защищает воду от изменений pH. Рассчитайте щелочность в пересчете на карбонат кальция, используя объем титра, концентрацию титра, объем пробы воды, поправочный коэффициент, основанный на методе титрования, и коэффициент пересчета в миллиэквивалентах в миллиграммы карбоната кальция.
Как рассчитать тест как 20% от оценки?
Вычисление значения вашего теста по итоговой оценке является простым делом. Узнайте, как сделать это в два простых шага.
Формула относительного стандартного отклонения
Формула относительного стандартного отклонения (Содержание)
Формула относительного стандартного отклонения
Формула для относительного стандартного отклонения
Relative Standard Deviation (RSD) = (S * 100) / x¯
Примеры формул относительного стандартного отклонения (с шаблоном Excel)
Давайте рассмотрим пример, чтобы лучше понять расчет относительного стандартного отклонения.
Рассчитайте относительное стандартное отклонение для следующего набора чисел: 48, 52, 56, 60, где стандартное отклонение составляет 2, 48.
Решение:
Среднее значение выборки рассчитывается как:
Относительное стандартное отклонение рассчитывается по формуле, приведенной ниже
Относительное стандартное отклонение (RSD) = (S * 100) / x
Таким образом, RSD для указанного числа составляет 4, 6.
Рассчитайте относительное стандартное отклонение для следующего набора чисел: 10, 20, 30, 40 и 50, где стандартное отклонение равно 10.
Решение:
Среднее значение выборки рассчитывается как:
Относительное стандартное отклонение рассчитывается по формуле, приведенной ниже
Относительное стандартное отклонение (RSD) = (S * 100) / x
Таким образом, RSD для указанного числа составляет 33, 33.
Рассчитайте относительное стандартное отклонение для следующего набора чисел: 8, 20, 40 и 60, где стандартное отклонение равно 5.
Решение:
Среднее значение выборки рассчитывается как:
Относительное стандартное отклонение рассчитывается по формуле, приведенной ниже
Относительное стандартное отклонение (RSD) = (S * 100) / x
объяснение
Относительное стандартное отклонение получается путем умножения стандартного отклонения на 100 и деления результата на среднее значение по группе. Он выражается в процентах и в основном обозначает, как различные числа располагаются относительно среднего значения. Он обычно используется для соотношения риска и доходности по нескольким инвестиционным предложениям, основанным на его исторической доходности.
Если конкретный продукт имеет более высокое относительное стандартное отклонение, это означает, что числа очень широко распространены от его среднего значения. Иногда, в соответствии с требованиями продукта, команда RSD нуждается в определенных данных, которые на самом деле очень далеки от среднего RSD. В этих случаях учитываются данные, которые хорошо отклоняются от ОСБ.
В случае обратной ситуации, то есть более низкого относительного стандартного отклонения, числа ближе, чем его среднее значение, и также известны как коэффициент вариации. Как правило, это дает представление о реальных прогнозах в рамках данного набора данных.
RSD указывает нам, является ли «обычное» стандартное отклонение минимальным или максимальным с точки зрения количества по сравнению со средним значением из ряда набора данных. Регулярное стандартное отклонение дает четкое представление о распределении баллов по среднему (среднему). Например, при среднем балле 50 и стандартном отклонении 10 большинство людей ожидают, что большинство баллов будет находиться в диапазоне от 40 до 60 и что почти все баллы упадут между 30 и 70.
Актуальность и использование формулы относительного стандартного отклонения
Калькулятор формулы относительного стандартного отклонения
Вы можете использовать следующий калькулятор относительного стандартного отклонения
Рекомендуемые статьи
Дисперсия, среднеквадратичное (стандартное) отклонение, коэффициент вариации в Excel
Из предыдущей статьи мы узнали о таких показателях, как размах вариации, межквартильный размах и среднее линейное отклонение. В этой статье изучим дисперсию, среднеквадратичное отклонение и коэффициент вариации.
Дисперсия
Дисперсия случайной величины – это один из основных показателей в статистике. Он отражает меру разброса данных вокруг средней арифметической.
Сейчас небольшой экскурс в теорию вероятностей, которая лежит в основе математической статистики. Как и матожидание, дисперсия является важной характеристикой случайной величины. Если матожидание отражает центр случайной величины, то дисперсия дает характеристику разброса данных вокруг центра.
Формула дисперсии в теории вероятностей имеет вид:
То есть дисперсия — это математическое ожидание отклонений от математического ожидания.
На практике при анализе выборок математическое ожидание, как правило, не известно. Поэтому вместо него используют оценку – среднее арифметическое. Расчет дисперсии производят по формуле:
s 2 – выборочная дисперсия, рассчитанная по данным наблюдений,
X – отдельные значения,
X̅– среднее арифметическое по выборке.
Стоит отметить, что у такого расчета дисперсии есть недостаток – она получается смещенной, т.е. ее математическое ожидание не равно истинному значению дисперсии. Подробней об этом здесь. Однако при увеличении объема выборки она все-таки приближается к своему теоретическому аналогу, т.е. является асимптотически не смещенной.
Простыми словами дисперсия – это средний квадрат отклонений. То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности. Разница между отдельным значением и средней отражает меру отклонения. В квадрат возводится для того, чтобы все отклонения стали исключительно положительными числами и чтобы избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании. Затем, имея квадраты отклонений, просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений. Отклонения возводятся в квадрат, и считается средняя. Теперь вы знаете, как найти дисперсию.
Расчет дисперсии в Excel
Генеральную и выборочную дисперсии легко рассчитать в Excel. Есть специальные функции: ДИСП.Г и ДИСП.В соответственно.
В чистом виде дисперсия не используется. Это вспомогательный показатель, который нужен в других расчетах. Например, в проверке статистических гипотез или расчете коэффициентов корреляции. Отсюда неплохо бы знать математические свойства дисперсии.
Свойства дисперсии
Свойство 1. Дисперсия постоянной величины A равна 0 (нулю).
Свойство 2. Если случайную величину умножить на постоянную А, то дисперсия этой случайной величины увеличится в А 2 раз. Другими словами, постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.
Свойство 3. Если к случайной величине добавить (или отнять) постоянную А, то дисперсия останется неизменной.
Свойство 4. Если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их дисперсий.
Свойство 5. Если случайные величины X и Y независимы, то дисперсия их разницы также равна сумме дисперсий.
Среднеквадратичное (стандартное) отклонение
Если из дисперсии извлечь квадратный корень, получится среднеквадратичное (стандартное) отклонение (сокращенно СКО). Встречается название среднее квадратичное отклонение и сигма (от названия греческой буквы). Общая формула стандартного отклонения в математике следующая:
На практике формула стандартного отклонения следующая:
Как и с дисперсией, есть и немного другой вариант расчета. Но с ростом выборки разница исчезает.
Расчет cреднеквадратичного (стандартного) отклонения в Excel
Для расчета стандартного отклонения достаточно из дисперсии извлечь квадратный корень. Но в Excel есть и готовые функции: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В (по генеральной и выборочной совокупности соответственно).
Среднеквадратичное отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными.
Коэффициент вариации
Значение стандартного отклонения зависит от масштаба самих данных, что не позволяет сравнивать вариабельность разных выборках. Чтобы устранить влияние масштаба, необходимо рассчитать коэффициент вариации по формуле:
По нему можно сравнивать однородность явлений даже с разным масштабом данных. В статистике принято, что, если значение коэффициента вариации менее 33%, то совокупность считается однородной, если больше 33%, то – неоднородной. В реальности, если коэффициент вариации превышает 33%, то специально ничего делать по этому поводу не нужно. Это информация для общего представления. В общем коэффициент вариации используют для оценки относительного разброса данных в выборке.
Расчет коэффициента вариации в Excel
Расчет коэффициента вариации в Excel также производится делением стандартного отклонения на среднее арифметическое:
Коэффициент вариации обычно выражается в процентах, поэтому ячейке с формулой можно присвоить процентный формат:
Коэффициент осцилляции
Еще один показатель разброса данных на сегодня – коэффициент осцилляции. Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.
Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных.
Таким образом, в статистическом анализе существует система показателей, отражающих разброс или однородность данных.
Ниже видео о том, как посчитать коэффициент вариации, дисперсию, стандартное (среднеквадратичное) отклонение и другие показатели вариации в Excel.