что такое тетраэдр в геометрии фото

22.11.202304.05.2022 admin 0 Comments

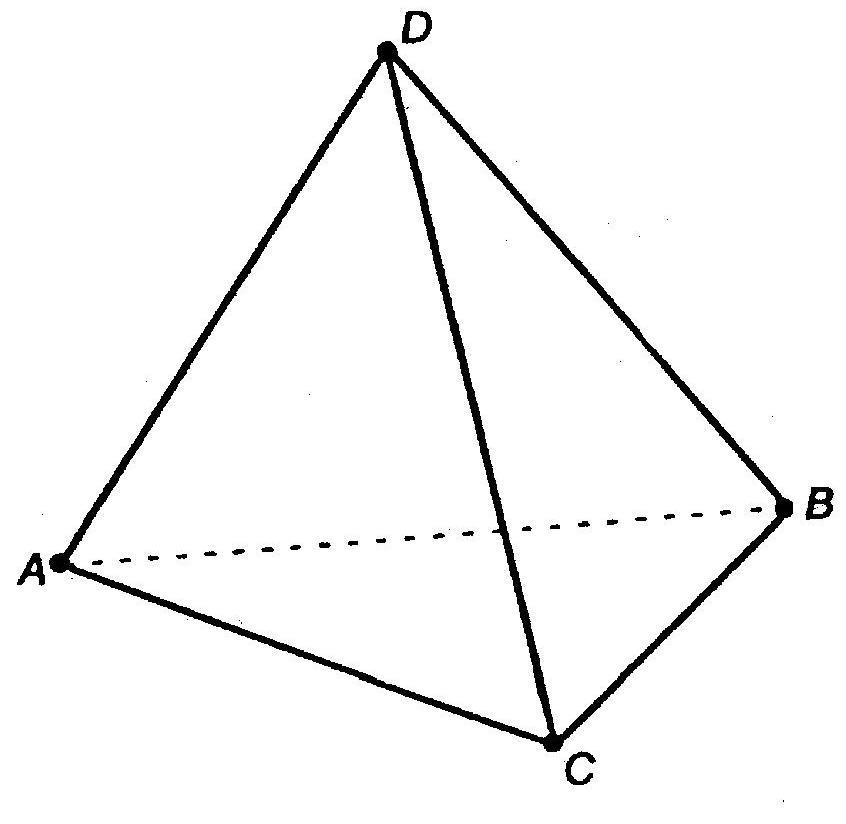
Тетраэдр

Тетраэдр имеет следующие характеристики:

Правильный тетраэдр составлен из четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольников. Следовательно, сумма плоских углов при каждой вершине равна 180°.
Тетраэдр не имеет центра симметрии, но имеет 3 оси симметрии и 6 плоскостей симметрии.

Является ли тетраэдр пирамидой? Да, тетраэдр это треугольная пирамида у которой все стороны равны.

Может ли пирамида быть тетраэдром? Только если это пирамида с треугольным основанием и каждая из её сторон равносторонний треугольник.

Отметим, что очень редко, но встречаются геометрические тела, составленные не из правильных треугольников, и их тоже называют тетраэдры, так как они имеют четыре грани.

Математические характеристики тетраэдра

Тетраэдр может быть помещен в сферу (вписан), так, что каждая из его вершин будет касаться внутренней стенки сферы.

Радиус описанной сферы тетраэдра определяется по формуле:

Сфера может быть вписана внутрь тетраэдра.

Радиус вписанной сферы тетраэдра определяется по формуле:

Площадь поверхности тетраэдра

Для наглядности, площадь поверхности тетраэдра можно представить в виде площади развёртки. Площадь поверхности можно определить как площадь одной из сторон тетраэдра (это площадь правильного треугольника) умноженной на 4. Либо воспользоваться формулой:

Объем тетраэдра определяется по следующей формуле:

Высота тетраэдра определяется по следующей формуле:

Расстояние до центра основания тетраэдра определяется по формуле:

Вариант развертки

Древнегреческий философ Платон ассоциировал тетраэдр с «земным» элементом огонь, поэтому для построения модели этого правильного многогранника мы выбрали красный цвет.

Заметим, что это не единственный вариант развертки.

Видео. Тетраэдр из набора «Волшебные грани»

Вы можете изготовить модель тетраэдра воспользовавшись деталями для сборки из набора «Волшебные грани».

Сборка многогранника из набора:

Подробная сборка от Алексея Жигулева (youtube-канал Оригами)

вращение готового многогранника:

Видео. Вращение всех правильных многогранников

Свойства тетраэдра, виды и формулы

Сегодня поговорим об элементах и свойствах тетраэдра, а также узнаем формулы нахождения у этих элементов площади, объема и других параметров.

Элементы четырехгранника

Вам будет интересно: Петрозаводский педагогический колледж: стать специалистом заочно

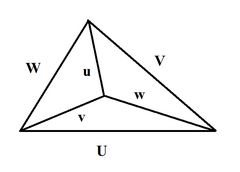
Отрезок, выпущенный из любой вершины тетраэдра и опущенный на точку пересечения медиан грани, являющейся противоположной, называется медианой.

Высота многоугольника представляет собой нормальный отрезок, опущенный из вершины напротив.

Бимедианой называется отрезок, соединяющий центры скрещивающихся ребер.

Свойства тетраэдра

1) Параллельные плоскости, которые проходят через два скрещивающихся ребра, образуют описанный параллелепипед.

3) Плоскость разделяет тетраэдр на две равные по объему части, если проходит через середину двух скрещивающихся ребер.

Виды тетраэдра

Видовое разнообразие фигуры достаточно широко. Тетраэдр может быть:

Остановимся подробно на правильном тетраэдре, свойства которого практически не отличаются.

Формулы четырехгранника

Высота тетраэдра равна произведению корня из 2/3 и длины ребра.

Объем тетраэдра находится так же, как объем пирамиды: корень квадратный из 2 разделить на 12 и умножить на длину ребра в кубе.

Остальные формулы для расчета площади и радиусов окружностей представлены выше.

Источник

Тетраэдр.

Тетраэдр — правильный многогранник (четырёхгранный), имеющий 4 грани, они, в свою очередь, оказываются правильными треугольниками. У тетраэдра 4 вершины, к каждой из них сходится 3 ребра. Общее количество ребер у тетраэдра 6.

Свойства тетраэдра.

Параллельные плоскости, которые проходят через пары рёбер тетраэдра, что скрещиваются, и определяют описанный параллелепипед около тетраэдра.

Плоскость, которая проходит сквозь середины 2-х рёбер тетраэдра, что скрещиваются, и делит его на 2 части, одинаковые по объему.

Все медианы и бимедианы тетраэдра пересекаются в одной точке. Эта точка делит медианы в отношении 3:1, если считать от вершины. Она же делит бимедианы на две равные части.

Типы тетраэдров.

У правильного тетраэдра каждый двугранный угол при рёбрах и каждый трёхгранный угол при вершинах имеют одинаковую величину.

Тетраэдр состоит из 4 граней, 4 вершин и 6 ребер.

Кроме правильного тетраэдра, заслуживают внимания такие типы тетраэдров:

— Равногранный тетраэдр, у него каждая грань представляет собой треугольник. Все грани-треугольники такого тетраэдра равны.

— Ортоцентрический тетраэдр, у него каждая высота, опущенная из вершин на противоположную грань, пересекается с остальными в одной точке.

— Прямоугольный тетраэдр, у него каждое ребро, прилежащее к одной из вершин, перпендикулярно другим ребрам, прилежащим к этой же вершине.

— Каркасный тетраэдр — тетраэдр, который таким условиям:

— Соразмерный тетраэдр, бивысоты у него одинаковы.

— Инцентрический тетраэдр, у него отрезки, которые соединяют вершины тетраэдра с центрами окружностей, которые вписаны в противоположные грани, пересекаются в одной точке.

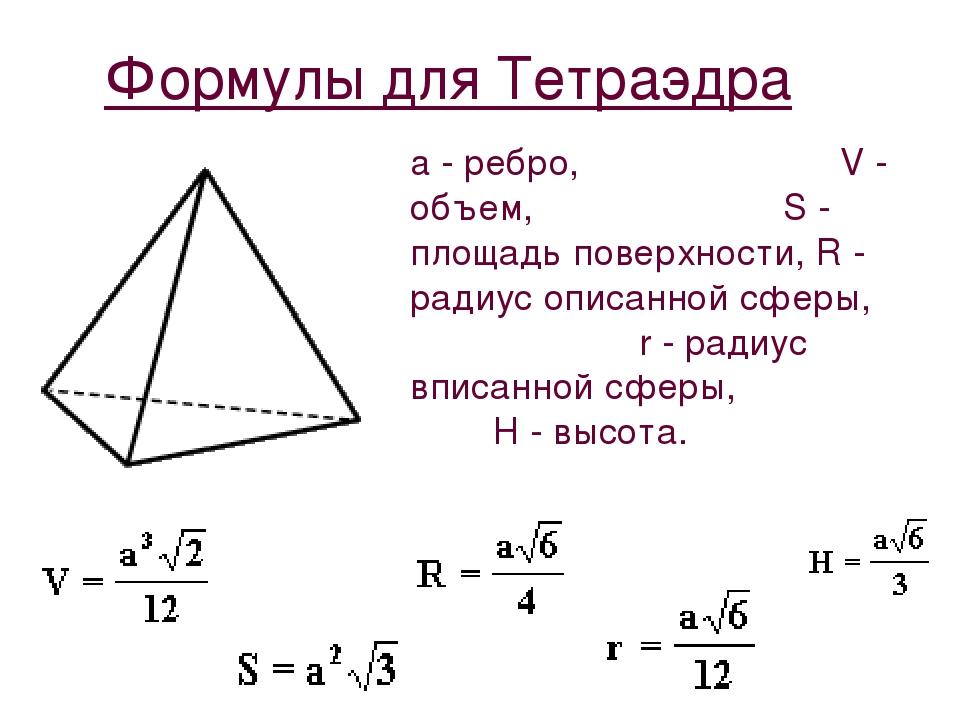
Формулы для определения элементов тетраэдра.

Высота тетраэдра:

Объем тетраэдра рассчитывается по классической формуле объема пирамиды. В нее нужно подставить высоту тетраэдра и площадь правильного (равностороннего) треугольника.

Основные формулы для правильного тетраэдра:

Источник

Презентация по геометрии на тему «Тетраэдр и его свойства»

Описание презентации по отдельным слайдам:

муниципальное автономное общеобразовательное учреждение средняя общеобразовательная школа № 45 Методическое пособие для учащихся 10 классов Составил учитель математики первой категории Гавинская Елена Вячеславовна. г.Калининград 2015-2016 учебный год

Определение. Многогранник, составленный из n-угольника А1А2A3…Аn и n треугольников с общей вершиной, называется пирамидой.

Многоугольник А1А2А3…Аn называется основанием, а треугольники- боковыми гранями пирамиды. Точка Р называется вершиной пирамиды, а отрезки РА1,РА2,…,РАn – ее боковыми ребрами. Пирамиду с основанием А1А2…Аn и вершиной Р обозначают : РА1А2…Аn и называют n-угольной пирамидой. Определение.

Перпендикуляр, проведенный из вершины пирамиды к плоскости основания, называется высотой пирамиды. Определение.

Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой. Определение.

Свойства правильной пирамиды. Все боковые ребра правильной пирамиды равны. Боковые грани правильной пирамиды являются равными равнобедренными треугольниками. Все апофемы правильной пирамиды равны друг другу. Двугранные углы при основании равны. Двугранные углы при боковых ребрах равны. Каждая точка высоты равноудалена от всех вершин основания. Каждая точка высоты равноудалена от всех боковых граней.

8. Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему : 9. В правильной треугольной пирамиде скрещивающиеся ребра взаимно перпендикулярны. 10. Плоскость, проходящая через высоту правильной пирамиды и высоту боковой грани, перпендикулярна к плоскости боковой грани. Sбок = ½ ∙ Росн ∙d

«плоскость, проходящая через середины двух ребер основания тетраэдра и вершину, не принадлежащую этому основанию, параллельна третьему ребру основания». Свойство тетраэдра:

Дано: РАВС – тетраэдр; М – середина АС: МА=МС; К – середина ВС: ВК=КС Доказать: (РМК)║ВС

Для любого тетраэдра справедлив аналог теоремы о пересечении медиан треугольника в одной точке, в которой они делятся в отношении 2:1, считая от вершины. Так, 6 плоскостей, проведенных через ребра тетраэдра и середины противолежащих ребер, пересекаются в одной точке – в центроиде тетраэдра. Медианами в тетраэдре называются отрезки, соединяющие его вершины с центроидами противоположных граней. Эти четыре отрезка всегда пересекаются в одной точке О и делятся в ней в отношении 3:1, считая от вершин. Медианы тетраэдра.

PABC– тетраэдр; РМ и АК – медианы тетраэдра; т.О – точка пересечения медиан тетраэдра РАВС.

Через точку О проходят и бимедианы – отрезки, соединяющие середины противоположных ребер тетраэдра, причем они делятся точкой О пополам. Бимедианы тетраэдра.

РАВС – тетраэдр; МН и КЕ – бимедианы тетраэдра, причем МО=ОН и КО=ОЕ.

Проведем через каждое ребро тетраэдра плоскость, параллельную противоположному ребру. Получим три пары параллельных плоскостей, ограничивающих параллелепипед, называемый описанным параллелепипедом тетраэдра. Ребра тетраэдра являются диагоналями граней параллелепипеда, середины ребер – их центроидами. Отсюда следует, что все бимедианы проходят через центр O параллелепипеда и делятся им пополам. Нетрудно увидеть, что медианы тетраэдра лежат на диагоналях граней параллелепипеда и также проходят через точку O. Центроид тетраэдра, как и центроид треугольника, является центром равных масс, помещенных в его вершины, – обстоятельство, которое можно использовать для доказательства приведенных выше свойств. Чисто геометрически их можно доказать с помощью следующей полезной конструкции.

Медианы тетраэдра «ведут себя примерно» – как и в треугольнике, они всегда проходят через одну и ту же точку. Иначе обстоит дело с высотами – перпендикулярами, опущенными из вершин тетраэдра на противоположные грани. Высоты треугольника пересекаются в одной точке – ортоцентре. То же верно и для правильных тетраэдров, в частности для правильных треугольных пирамид. Ортоцентрический и прямоугольный тетраэдры.

И все же ортоцентр существует у достаточно широкого класса тетраэдров. Они так и называются – ортоцентрические тетраэдры. Любой из них можно получить, взяв в качестве основания произвольный треугольник и соединив его вершины с любой точкой на перпендикуляре к его плоскости, восстановленном из его ортоцентра. И обратно, основания всех высот ортоцентрического тетраэдра – ортоцентры его граней.

Приведем еще несколько критериев (т.е. необходимых и достаточных условий) ортоцентричности: тетраэдр является ортоцентрическим тогда и только тогда, когда его противоположные ребра перпендикулярны; или середины всех шести ребер лежат на одной сфере; или все ребра описанного параллелепипеда равны. Некоторые свойства треугольника, связанные с ортоцентром, например, теорема о прямой Эйлера и об окружности девяти точек в соответственно измененном виде, можно найти и у ортоцентрического тетраэдра.

Центроид ортоцентрического тетраэдра лежит на отрезке между ортоцентром H и центром описанной сферы O и делит этот отрезок пополам, а точка, которая разбивает отрезок OH в отношении 1:2 является центром «сферы 12 точек» – на ней лежат ортоцентры и центроиды всех граней, а также точки, делящие отрезки от H до вершин в отношении 1:2. Об одном виде ортоцентрических тетраэдров стоит сказать отдельно – о тетраэдре, в вершине М которого сходятся три взаимно перпендикулярных ребра. Очевидно, эта вершина M и будет его ортоцентром. Такой тетраэдр называется прямоугольным. Для него выполняется своего рода «теорема Пифагора»: «Если S1, S2, S3 – площади его прямоугольных граней («катетов»), а S – площадь четвертой грани («гипотенузы»), то: S2= S12+ S22+ S32».

Правильный тетраэдр. Правильный тетраэдр – это тетраэдр, все грани которого – равносторонние треугольники.

Теоремы, отражающие особые свойства правильного тетраэдра. В правильном тетраэдре отрезки, соединяющие центры граней, равны друг другу. Центры граней правильного тетраэдра являются вершинами другого правильного тетраэдра.

Доказательство первого свойства. Дано: МРКН – правильный тетраэдр; т.А, т.В, т.С, т.Е – соответственно центры граней правильного тетраэдра: МРН, МРК, КРН, МКН. Доказать: АВ=ВС=АС=АЕ=ВЕ=СЕ

Доказательство второго свойства. Дано: МРКН – правильный тетраэдр; т.А, т.В, т.С, т.Е – соответственно центры граней правильного тетраэдра: МРН, МРК, КРН, МКН. Доказать: АВСЕ – правильный тетраэдр.

Менее симметричны правильные треугольные пирамиды (т.е. тетраэдры с равными гранями – 3 оси симметрии). Правильная пирамида переходит сама в себя при поворотах вокруг высоты на 120˚и 240˚ (Рис.2).

Сечения тетраэдра. Т.к. тетраэдр имеет четыре грани, то в сечении могут получаться либо треугольники, либо четырехугольники.

Особые пирамиды и тетраэдры.

Семиголовковая пирамида. Одна из вершин заметна сразу, остальные же немного труднее найти. Пирамида Шивы.

Энергетический звёздный тетраэдр. Вокруг женщины. Вокруг мужчины.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-107432

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

В Госдуме предлагают сделать бесплатным проезд на общественном транспорте для детей до 16 лет

Время чтения: 2 минуты

На новом «Уроке цифры» школьникам расскажут о разработке игр

Время чтения: 1 минута

Вопрос о QR-кодах для сотрудников школ пока не обсуждается

Время чтения: 2 минуты

Попова предложила изменить школьную программу по биологии

Время чтения: 1 минута

Российские школьники установили рекорд на олимпиаде по астрономии

Время чтения: 2 минуты

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

СОДЕРЖАНИЕ

Правильный тетраэдр

В правильном тетраэдре все грани имеют одинаковый размер и форму (конгруэнтны), и все ребра имеют одинаковую длину.

Координаты правильного тетраэдра

Следующие декартовы координаты определяют четыре вершины тетраэдра с длиной ребра 2 с центром в начале координат и двумя ребрами уровня:

Тетраэдр: (1,1,1), (1, −1, −1), (−1,1, −1), (−1, −1,1) Двойственный тетраэдр: (−1, −1, −1), (−1,1,1), (1, −1,1), (1,1, −1)

Углы и расстояния

Для правильного тетраэдра с длиной ребра а :

Изометрии правильного тетраэдра

Ортогональные проекции правильного тетраэдра

Ортографическая проекция

В центре	Лицо / вершина	Край
Изображение
Проективная симметрия	[3]	[4]

Поперечное сечение правильного тетраэдра

Это свойство также применяется к тетрагональным дифеноидам при применении к двум специальным парам ребер.

Сферическая черепица

Спиральная укладка

Другие особые случаи

что такое тетраэдр в геометрии фото. Смотреть фото что такое тетраэдр в геометрии фото. Смотреть картинку что такое тетраэдр в геометрии фото. Картинка про что такое тетраэдр в геометрии фото. Фото что такое тетраэдр в геометрии фото

Отношения подгруппы тетраэдрической симметрии

Тетраэдрические симметрии показаны на тетраэдрических диаграммах

Изометрии неправильных тетраэдров

Общие свойства

Объем

Объем тетраэдра определяется формулой объема пирамиды:

Абсолютное значение скалярного тройного произведения можно представить в виде следующих абсолютных значений определителей:

Если мы не требуем, чтобы d = 0, то

Учитывая расстояния между вершинами тетраэдра, объем можно вычислить с помощью определителя Кэли-Менгера :

В приведенной выше формуле используются шесть длин ребер, а в следующей формуле используются три длины ребер и три угла.

Формула типа Герона для объема тетраэдра

Делитель объема

Неевклидова книга

Расстояние между краями

Свойства, аналогичные свойствам треугольника

Тетраэдр обладает многими свойствами, аналогичными свойствам треугольника, включая внутреннюю сферу, описанную сферу, средний тетраэдр и внешние сферы. Он имеет соответствующие центры, такие как центр окружности, центр окружности, эксцентриситет, центр Шпикера и такие точки, как центроид. Однако обычно нет ортоцентра в смысле пересечения высот.

Ортогональная линия, опущенная от точки Монжа к любой грани, пересекает эту грань в середине отрезка прямой между ортоцентром этой грани и основанием высоты, опущенной из противоположной вершины.

Радиус двенадцатигранной сферы составляет одну треть описанного радиуса контрольного тетраэдра.

Существует соотношение между углами, образованными гранями общего тетраэдра, определяемое выражением

Геометрические отношения

Включение тетраэдров внутрь правильного соединения пяти кубов дает еще два правильных соединения, содержащих пять и десять тетраэдров.

Обычные тетраэдры не могут замощить пространство сами по себе, хотя этот результат кажется достаточно вероятным, чтобы Аристотель утверждал, что это возможно. Однако два правильных тетраэдра могут быть объединены с октаэдром, давая ромбоэдр, который может замостить пространство.

Если ослабить требование, чтобы все тетраэдры были одинаковой формы, можно разбить пространство, используя только тетраэдры, разными способами. Например, можно разделить октаэдр на четыре одинаковых тетраэдра и снова объединить их с двумя правильными. (В качестве примечания: эти два вида тетраэдров имеют одинаковый объем.)

Тетраэдр уникален среди однородных многогранников тем, что не имеет параллельных граней.

Закон синусов для тетраэдров и пространство всех форм тетраэдров

Можно рассматривать две стороны этого тождества как соответствующие ориентации поверхности по часовой стрелке и против часовой стрелки.

Если поставить любую из четырех вершин в роли O, мы получим четыре таких тождества, но не более трех из них являются независимыми: если стороны трех из них умножаются по часовой стрелке, и получается, что произведение равно произведению «против часовой стрелки» стороны одних и тех же трех тождеств, а затем общие множители отменяются с обеих сторон, в результате получается четвертая идентичность.

Закон косинусов для тетраэдров

Закон косинусов для этого тетраэдра, который относится к области граней тетраэдра к двугранным углам вокруг вершины, определяются следующим соотношением:

Внутренняя точка

Inradius

Обозначая внутренний радиус тетраэдра как r, а внутренние радиусы его треугольных граней как r _i для i = 1, 2, 3, 4, имеем

с равенством тогда и только тогда, когда тетраэдр правильный.

Circumradius

Кругоцентр

В отличие от центроида, центр описанной окружности не всегда может лежать внутри тетраэдра. Аналогично тупому треугольнику центр описанной окружности находится вне объекта для тупого тетраэдра.

Центроид

Сумма площадей любых трех граней больше площади четвертой грани.

Целочисленные тетраэдры

Тетраэдр может иметь целочисленный объем и последовательные целые числа в качестве ребер, например, с ребрами 6, 7, 8, 9, 10 и 11 и объемом 48.

Родственные многогранники и соединения

Имя тетраэдра				Край Эквивалентность диаграмма	Описание
Симметрия
Schön.	Кокс.	Сфера.	Ord.
Правильный тетраэдр
Название антипризмы	Дигональная антипризма	(Тригональная) Треугольная антипризма	(Тетрагональная) Квадратная антипризма		Пятиугольная антипризма	Шестиугольная антипризма	Семиугольная антипризма	Восьмиугольная антипризма	Эннеагональная антипризма	Десятиугольная антипризма	Хендекагональная антипризма	Додекагональная антипризма	.	Апейрогональная антипризма
Изображение многогранника												.
Сферическое мозаичное изображение								Плоское мозаичное изображение
Конфигурация вершины.	2.3.3.3	3.3.3.3	4.3.3.3	5.3.3.3	6.3.3.3	7.3.3.3	8.3.3.3	9.3.3.3	10.3.3.3	11.3.3.3	12.3.3.3	.	∞.3.3.3

* n 32 изменение симметрии правильных мозаик: <3, n >
Сферический				Евклид.	Компактный гипер.		Paraco.	Некомпактный гиперболический

3.3	3 3	3 4	3 5	3 6	3 7	3 8	3 ∞	3 12i	3 9i	3 6i	3 3i