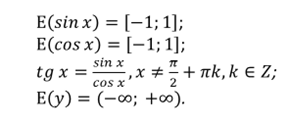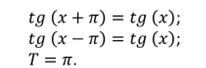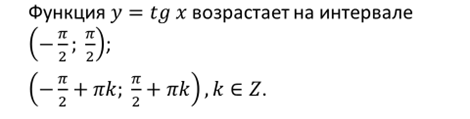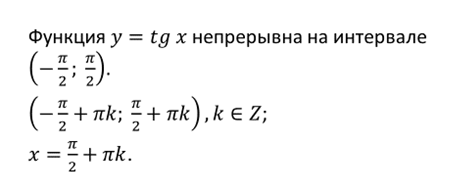что такое tgx в математике

Алгебра и начала математического анализа. 11 класс

Конспект урока

Алгебра и начала математического анализа, 11 класс

Урок №5. Свойства и график функции y=tgx и y=ctg x

Перечень вопросов, рассматриваемых в теме

Асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении от начала координат этой точки по кривой.

Тангенсоида –график функции у = tgx; плоская кривая, изображающая изменение тангенса в зависимости от изменения его аргумента (угла).

Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2010.–336 с.

Шахмейстер, А.Х. Тригонометрия / А.Х. Шахмейстер.— СПб.: Петроглиф, 2014. — 750 с.

Открытые электронные ресурсы:

Открытый банк заданий ЕГЭ ФИПИ [Электронный ресурс].–Режим доступа: http://ege.fipi.ru/

Решу ЕГЭ образовательный портал для подготовки к экзаменам [Электронный ресурс].– Режим доступа: https://ege.sdamgia.ru/

Теоретический материал для самостоятельного изучения

1. ;

2.

Ответ:

Объяснение нового материала

Изучение свойств функции y=tgx начнем с построения графика. Обратимся к единичной окружности:

рис.1 Тригонометрический круг

Переносим основные значения углов на координатную плоскость. По оси абсцисс откладываем угол в радианах, по оси ординат – значения тангенса угла.

рис.2 График y=tgx на промежутке

Как любая тригонометрическая функции, функция тангенса периодическая, делая параллельный перенос получаем:

Заметим, что график симметричен относительно начала координат, следовательно функция тангенса нечётная. Используя построенный нами график, выведем основные свойства y=tgx:

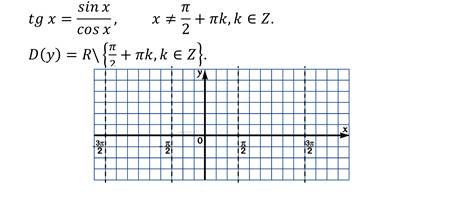
1. Область определения функции y = tgx все действительные числа, кроме чисел вида

3. Функция нечётная, т.к. . График нечётной функции симметричен относительно начала координат;

4. Функция возрастает на всём интервале;

5. Функция не ограничена ни снизу, ни сверху. Функция не имеет ни наибольшего, ни наименьшего значений;

6.

7. Функция принимает:

Для построения графика можно придерживаться алгоритму рассмотренному при построении графика , однако (формула приведения). Т.е. смещая тангенсоиду на единиц влево и делаем симметрию относительно оси Ох за счёт коэффициента –1, получаем:

Основные свойства y=сtgx:

1. Область определения функции y = сtgx все действительные числа, кроме чисел вида

2. Функция периодическая с периодом ;

3. Функция нечётная. График нечётной функции симметричен относительно начала координат;

4. Функция убывает на всём интервале;

5. Функция не ограничена ни снизу, ни сверху. Функция не имеет ни наибольшего, ни наименьшего значений;

6. .

Примеры и разборы решения заданий тренировочного модуля:

Найдем все корни уравнения , принадлежащие отрезку .

Построим графики функций и (рис. 6)

Рис. 4 – графики функций и .

Графики пересекаются в трёх точках, абсциссы которых являются корнями уравнения .

Ответ:

Пример 2. Найти все решения неравенства , принадлежащие отрезку .

рис.5 графики функций и

Графики пересекаются в трёх точках, абсциссы которых являются корнями уравнения .

Ответ:

Источник

Объяснение и обоснование

Этот результат можно получить и геометрически. Значения тангенса – это ордината соответствующей точки на линии тангенсов (рис.91). Поскольку точки Aи B единичной окружности лежат на прямых ОА и ОВ, параллельных линии тангенсов, мы не сможем найти значение тангенса дляx, kZ.

Для всех других значений аргумента мы можем найти соответствующую точку на линии тангенсов и ее ординату — тангенс. Следовательно, все

Значенияx входят в область определения функции y=tgx.

Для точек единичной окружности (которые не совпадают с точками А и В) ординаты соответствующих т

очек на линии тангенсов принимают

все значения до +, поскольку для любого действительного числа

мы можем указать соответствующую точку на оси ординат, а значит, и соответствующую точку на оси тангенсов. Учитывая, что точка О лежит

внутри окружности, а точка вне ее (или на самой окружности), получаем, что прямая имеет с окружностью хотя бы одну общую точку

(на самом деле их две). Следовательно, для любого действительного числа

найдется аргумент х, такой, что tan x равен данному действительному числу.

то есть R. Это можно записать так: E (=tgx) = R. Отсюда следует, что наибольшего и наименьшего значений функция tan x не имеет.

Как было показано в § 13, тангенс — нечетная функция:tg(-x)=tg x, следовательно, ее график симметричен относительно начала координат.

Тангенс — периодическая функция с наименьшим положительным периодом

Поэтому при построении графика

этой функции достаточно построить график на любом промежутке длиной π,

а потом полученную линию перенести параллельно вправо и влево вдоль оси

Ox на расстоянияkT = πk, где k — любое натуральное число.

Чтобы найти точки пересечения графика функции с осями координат,

напомним, что на оси Oy значение x = 0. Тогда соответствующее значение

y = tg 0 = 0, то есть график функции y = tg x проходит через начало координат.

На оси Ox значение y = 0. Поэтому необходимо найти такие значения x,

при которых tg x, то есть ордината соответствующей точки линии тангенсов, равна нулю. Это будет тогда и только тогда, когда на единичной окружности будут выбраны точки C или D, то есть при x = πk, k ∈ Z.

Промежутки знакопостоянства. Как было обосновано в § 13, значения

функции тангенс положительны (то есть ордината соответствующей точкилинии тангенсов положительна) в І и ІІІ четвертях. Следовательно, tgx > 0 при

а также, учитывая период, при всех

Значения функции тангенс отрицательны (то есть ордината соответствующей точки линии тангенсов отрицательна) во ІІ и ІV четвертях. Такимобразом,

Промежутки возрастания и убывания.

Учитывая периодичность функции tgx (период T = π), достаточно исследовать ее на возрастание и убывание на любом промежутке длиной π,

тангенсов увеличивается (то есть tgx2>tgx1). Таким образом, на этом

промежутке функция tgx возрастает. Учитывая периодичность функции

tgx, делаем вывод, что она возрастает также на каждом из промежутков

Проведенное исследование позволяет обоснованно построить график

функции y = tg x. Учитывая периодичность этой функции (с периодом π),

линии тангенсов. На рисунке 93 показано построение графика функции

y = tg x на промежутке.

Далее, учитывая периодичность тангенса (с периодом π), повторяем вид

графика на каждом промежутке длиной π (то есть параллельно переносим

график вдоль оси Ох на πk, где k — целое число).

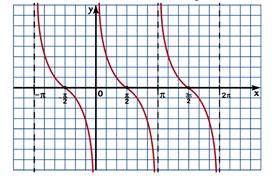
Получаем график, приведенный на рисунке 94, который называется тангенсоидой.

14.4. СВОЙСТВА ФУНКЦИИ y = ctg x И ЕЕ ГРАФИК

Объяснение и обоснование

Так как =, то областью определения котангенса будут все значения аргумента, при которых sin х ≠ 0, то есть x ≠ πk, k ∈ Z. Такимобразом,

D (ctg x): x ≠ πk, k ∈ Z.

Тот же результат можно получить, используя геометрическую иллюстрацию. Значение котангенса — это абсцисса соответствующей точки на линии

котангенсов (рис. 95).

Поскольку точки А и В единичной окружности лежат на прямых ОА

и ОВ, параллельных линии котангенсов, мы не можем найти значение котангенса для x = πk, k ∈ Z. Длядругихзначенийаргументамыможемнайтисоответствующуюточкуна линии котангенсов и ее абсциссу — котангенс. Поэтому все значения x ≠ πk входят в область определения функции у = ctg х.

Для точек единичной окружности (которые не совпадают с точками А и В) абсциссы соответствующих точек на линии котангенсов принимают все значения от –× до +×, поскольку для любого действительного числа мы можем указать соответствующую точку на оси абсцисс, а значит, и соответствующую точку Qх на оси котангенсов. Учитывая, что точка О лежит внутри окружности, а точка Qх — вне ее (или на самой окружности), получаем, что прямая ОQх имеет с окружностью хотя бы одну общую точку (на самом деле их две). Следовательно, для любого действительного числа найдется аргумент х, такой, что сtg x равен данному действительному числу. Таким образом, область значений функции y = ctg x — все действительные числа, то есть R.

Это можно записать так: E (ctgx) = R.Из приведенных рассуждений также вытекает, что наибольшего и наименьшего значений функция ctgxне имеет.

Там же было обосновано, что котангенс — периодическая функция с наи­меньшим положительным периодом T= : ctg (x+ ) = ctg x, поэтому через промежутки длиной п вид графика функции ctgxповторяется.

Чтобы найти точки пересечения графика функции с осями координат, напомним, что на оси Oyзначение x= 0. Но ctg0 не существует, значит, график функции y= ctg x не пересекает ось Oy.

На оси Оx значение y= 0. Поэтому необходимо найти такие значения x, при которых ctgx, то есть абсцисса соответствующей точки линии котанген­сов, равна нулю. Это будет тогда и только тогда, когда на единичной окруж­ности будут выбраны точки C или D(рис. 95), то есть при

Значения функции котангенс отрицательны (то есть абсцисса соответ­ствующей точки линии котангенсов отрицательна) во II и IV четвертях, та­ким образом, ctgx x₁) аб­сцисса соответствующей точки линии котангенсов уменьшается (то есть ctgx₂

Источник

Функции y=tgx, ctg x. Их свойства и графики

Урок 18. Алгебра 10 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Функции y=tgx, ctg x. Их свойства и графики»

· рассмотреть тангенс и котангенс как функции аргумента x;

· познакомиться с основным свойствам функций y=tg x, ctg x;

· построить графики функций y=tg x, ctg x.

Для того, чтобы найти область определения функции y = tg x давайте ещё раз вспомним определение тангенса x.

Найдём область значений функции y = tg x.

Найдём период функции y = tg x. И исследуем её на чётность.

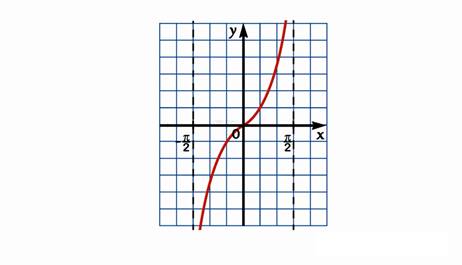
Поскольку функция y = tg x – периодичная функция с периодом π, то можно построить график функции на промежутке [-π/2; π/2], а затем сдвинуть построенную ветвь влево и вправо на π, 2π, 3π и так далее.

Поскольку функция нечётная, то можно построить на промежутке [0; π/2] и отобразить относительно начала координат.

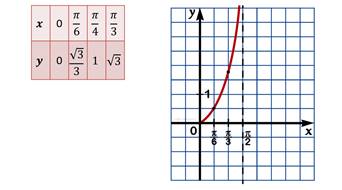
Для построения графика на промежутке [0; π/2], составим таблицу значений тангенса для основных точек из этого промежутка. Отметим эти точки на координатной плоскости.

Отобразим полученную часть графика относительно начала координат.

Сдвинем построенную ветвь влево и вправо на π.

По построенному графику легко определить основные свойства функции y = tg x.

Исследование на монотонность.

Исследование на ограниченность.

Наибольшее и наименьшее значение функции.

Исследование на непрерывность.

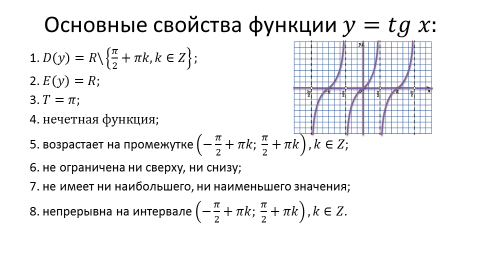
Давайте, ещё раз перечислим все свойства функции y = tg x.

Проведя аналогичные рассуждения, можно построить график функции y = ctg x на промежутке [0; π], затем отразить симметрично относительно начала координат и сдвинуть получившуюся ветвь влево и вправо.

Давайте, перечислим все свойства функции y = ctg x.

Источник

Урок «Функции y = tgx, y = ctgx, их свойства и графики»

Краткое описание документа:

В этом видеуроке рассмотрены свойства функций у = tgx, y = ctgx, показано, как построить их графики.

Видеоурок начинается с рассмотрения функции у = tgx.

Выделены свойства функции.

2) Функция у = tgxявляется периодической, где основной период равенπ. Это подтверждает равенство tg (x – π)=tg x = tg (x + π).Эти равенства изучались ранее, автор предлагает ученикам вспомнить их, указывая, что для любого допустимого значения tсправедливы равенства:

Далее перейдем к построению графика функции у = tgx. Как следует из свойств функции, описанных выше, функция у = tgx периодическая и нечетная. Поэтому достаточно построить часть графика – одну ветвь в одном промежутке, а затем воспользоваться симметрией для переноса. Автор приводит таблицу, в которой рассчитываются значения tgx при определенных значениях xдля более точного построения графика. Данные точки отмечаются на оси координат и соединяются плавной линией. Т.к. график симметричен относительно начала координат, то строится такая же ветвь, симметричная началу координат. В результате получаем одну ветвь графика у = tgx. Далее с помощью сдвига по оси х наπ, 2 πи так далее получается график у = tgx.

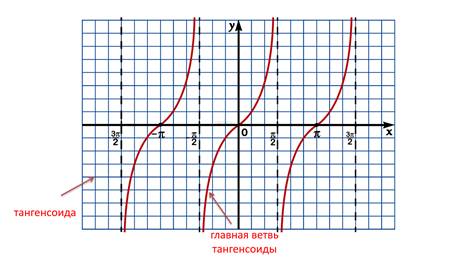
График функции у = tgx называется тангенсоида, а три ветви графика, показанные на рисунке – главные ветви тангенсоиды.

4) Функция у = tgx на каждом из промежутков (– + ; + ) возрастает.

5) График функции у = tgx не имеет ограничений сверху и снизу.

6) Функция у = tgx не имеет наибольшего и наименьшего значения.

7) Функция у = tgx непрерывна на любом промежутке (-–π/2+π;π/2+π). Прямая π/2+π называется асимптотой графика функции у = tgx, т.к. в этих точках график функции прерывается.

8) Множеством значений функции у = tgxназываются все действительные числа.

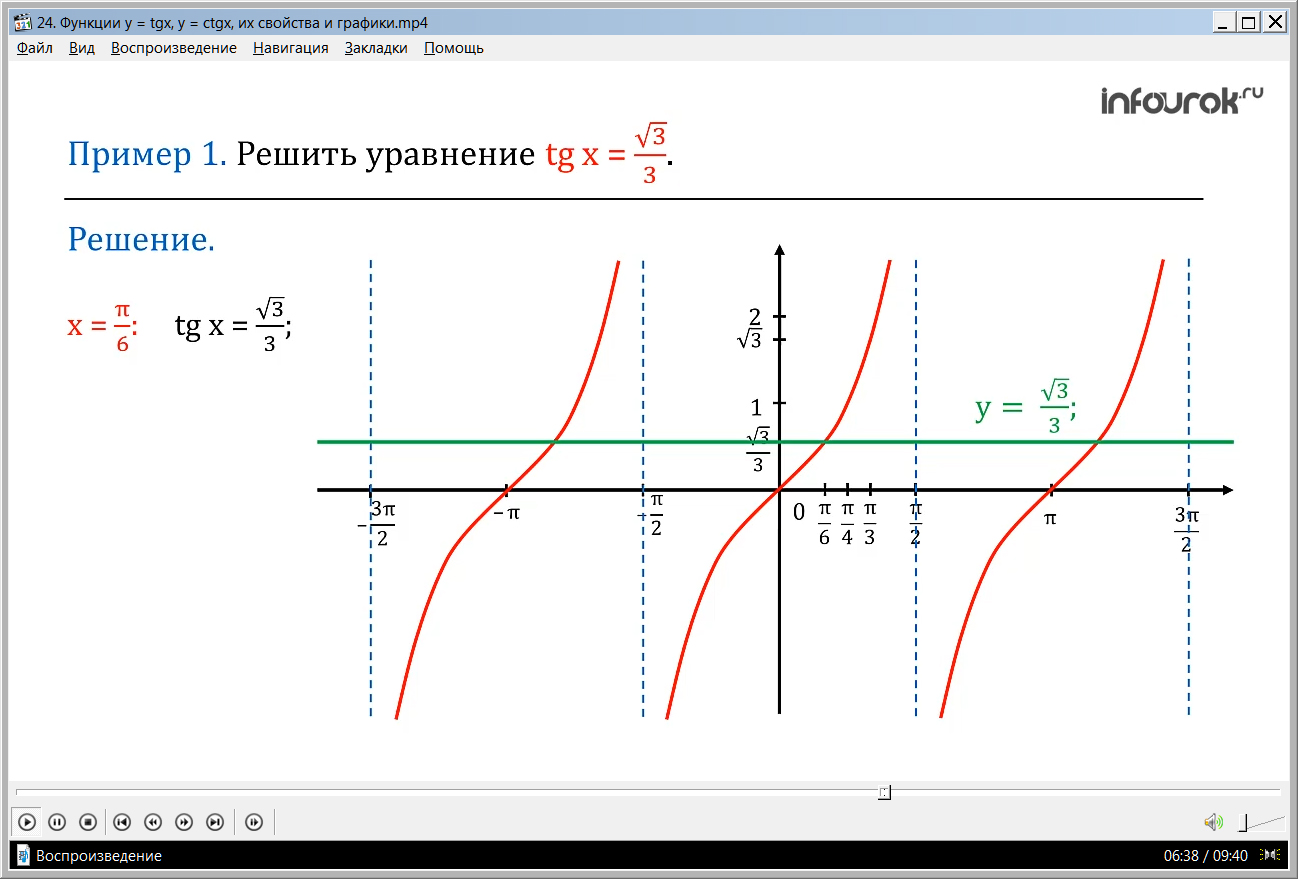
Далее в видеоуроке дается пример: решить уравнение с tgx. Для решения построим 2 графика функции у и найдем точки пересечения этих графиков: это бесконечное множество точек, абсциссы которых отличаются на πk. Корнем данного уравнения будет х = π/6 +πk.

Рассмотрим график функции у = ctgx. График функции можно построить двумя способами.

Первый способ предполагает построение графика аналогично построению графика функции у = tgx. Построим одну ветвь графика функции у = сtgxв промежутке между прямыми х = 0и х = π. Затем с помощью симметрии и периодичности построим другие ветви графика.

Второй способ более простой. График функции у = сtgxможно получить путем преобразования тангенсоиды с помощью формулы приведения сtgx = – tg (x + π/2). Для этого сдвинем одну ветвь графика функции у = tgxвдоль оси абсцисс на π/2вправо. Остальные ветви получаем путем сдвига этой ветви по оси х наπ, 2π и так далее. График функции у = ctgx называется также тангенсоида, а ветвь графика в промежутке (0;π) – главная ветвь тангенсоиды.

Мы рассмотрим свойства функции у = tg x ( игрек равно тангенс икс), у = ctg x( игрек равно котангенс икс), построим их графики. Рассмотрим функцию y = tgx

Прежде, чем строить график функции у = tg x, запишем свойства этой функции.

СВОЙСТВО 1. Областью определения функции у = tg x являются все действительные числа, кроме чисел вида х = + πk (икс равен сумме пи на два и пи ка).

СВОЙСТВО 2. Функция у = tg x является периодической с основным периодом π. (Так как справедливо двойное равенство

tg( x– π) = tgx = tg (x+π) тангенс от икс минус пи равен тангенсу икс и равен тангенсу от икс плюс пи). Это равенство мы рассматривали при изучении тангенса и котангенса. Напомним его:

Для любого допустимого значения t справедливы равенства:

Построим график функции у = tg x

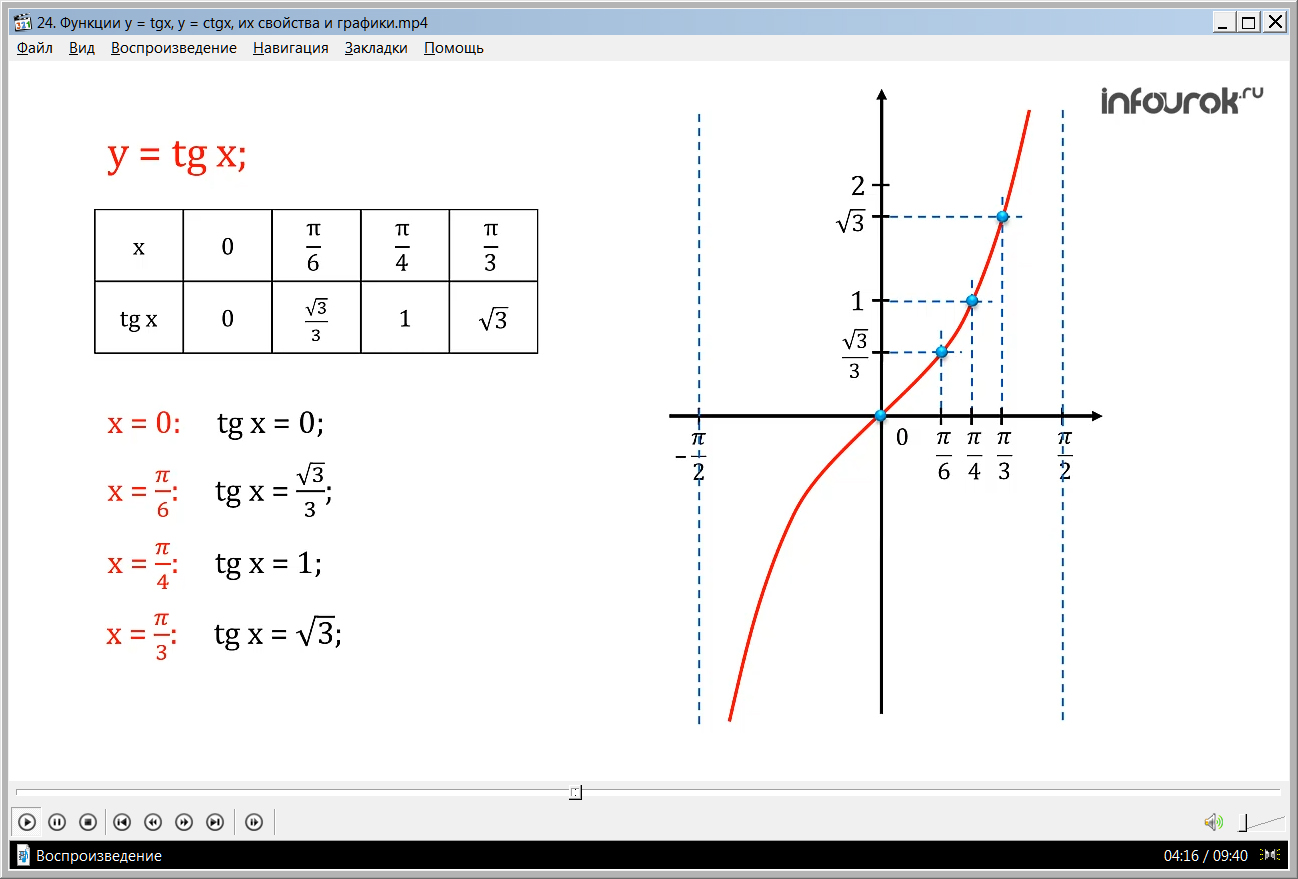
Построим таблицу значений тангенса для построения графика.

Находим первую точку: зная, что при х = 0 tg x = 0( икс равном нулю тангенс икс тоже равен нулю); следующая точка: при х = tg x = ( икс равном пи на шесть тангенс икс равен корень из трех на три); отметим следующие точки: при х = tg x = 1 (икс равном пи на четыре тангенс икс равен единице), а при х = tg x = ( икс равном пи на три тангенс икс равен корню квадратному из трех). Отметив полученные точки на координатной плоскости и соединим их плавной линией (рис. 2).

Так как график функции симметричен относительно начала координат, то построим такую же ветвь симметрично начала координат. (рис.3).

И, наконец, применив периодичность, получим график функции у = tg x.

Построенный график называется тангенсоида.

Изображенную на рисунке 3 часть тангенсоиды называют главной ветвью тангенсоиды.

На основании графика запишем еще свойства этой функции.

СВОЙСТВО 4. Функция у = tg x возрастает на каждом из промежутков (от минус пи на два плюс пи ка до пи на два плюс пи ка).

СВОЙСТВО 5. Функция у = tg x не ограничена ни сверху, ни снизу.

СВОЙСТВО 6. Функция у = tg x не имеет ни наибольшего, ни наименьшего значений.

СВОЙСТВО 7. Функция у = tg x непрерывна на любом интервале вида ( от минус пи на два плюс пи ка до пи на два плюс пи ка).

Прямая вида х = + πk (икс равно сумме пи на два и пи ка) является вертикальной асимптотой графика функции, так как в точках вида х = + πk функция терпит разрыв.

СВОЙСТВО 8. Множеством значений функции у = tg x являются все действительные числа, то есть ( е от эф равно промежутку от минус бесконечности до плюс бесконечности).

ПРИМЕР 1. Решить уравнение tg x = (тангенс икс равен корень из трех на три).

Решение. Построим в одной системе координат графики функций у = tg x

(игрек равен тангенсу икс) и у = ( игрек равен корню из трех, деленному на три).

Все решения данного уравнения запишем формулой х = + πk ( икс равно пи на шесть плюс пи ка).

Построим график функции у = сtg x.

Рассмотрим два способа построения.

Первый способ аналогичен построению графика функции у = tg x.

Воспользуемся таблицей значений котангенса для построения графика.

Отметив полученные точки на координатной плоскости и соединим их плавной линией.

Применим периодичность, получим график функции у = сtg x.

Мы построили ветвь графика функции у = сtg x в полосе от х = 0 и х =π. Строим остальные ветви путем сдвига построенной ветви по оси x на π, – π, 2π, – 2π и так далее.

Второй способ построения графика функции у =сtg x.

Получить график функции у =сtg x проще всего с помощью преобразования тангенсоиды, используя формулу приведения ( котангенс икс равно минус тангенс от суммы икс и пи на два).

При этом сначала, сдвинем ветвь графика функции у =tg x вдоль оси абсцисс на вправо, получим

у = tg (x+ ), а затем выполняем симметрию полученного графика относительно оси абсцисс. В результате получится ветвь графика функции у =сtg x (рис.4). Зная одну ветвь, можем построить весь график используя периодичность функции. Строим остальные ветви путем сдвига построенной ветви по оси x на π, 2π, и так далее.

График функции у =сtg x называется тоже тангенсоида, как и график функции у =tg x. Ветвь, которая заключена в промежутке от нуля до пи, называют главной ветвью графика функции у =сtg x.

Источник