что такое transposed convolution
Русские Блоги
[Transposed Convolution] Когда вы хотите использовать обучение для повышения
Концепция деконволюции впервые появилась в статье, опубликованной Zeiler в 2010 году.Deconvolutional networks, Но не указали название деконволюции, формальное использование термина деконволюция происходит в его последующей работеAdaptive deconvolutional networks for mid and high level feature learning). С успешным применением деконволюции в визуализации нейронных сетей,Он был принят во все большем количестве работ, таких как: сегментация сцены, генеративная модель и т. Д.Деконволюция также имеет много других названий, таких как: Транспонированная Свертка, Дробная Сверточная Свертка и так далее.
Трансфер из:
Поймите деконволюцию в одной статье, перенесите свертку
предисловие
Эта статья была переведена с《Up-sampling with Transposed Convolution》Эта статья имеет хорошее объяснение транспонированной свертки и деконволюции, здесь она переведена на китайский для китайцев.
Если есть какие-либо ошибки, пожалуйста, свяжитесь с нами. Пожалуйста, укажите источник для перепечатки.
Контактная информация:
e-mail: [email protected]
QQ: 973926198
github: https://github.com/FesianXu
Повышение частоты с транспонированной сверткой
Требования к усыновлению
Когда мы используем нейронные сети для генерации изображений, нам часто приходится конвертировать некоторые изображения с низким разрешением в изображения с высоким разрешением.
Для этой операции повышающей дискретизации в настоящее время существует несколько методов интерполяции для обработки:
Почему транспонированная свертка
Транспонированная свертка (Transposed Convolution) в некоторых литературах часто называется деконволюцией и дробно-шаговой конволюцией, потому что это легко думать и обрабатывать цифровой сигнал, потому что она называется деконволюцией Середина и деконволюция смешиваются, вызывая ненужные недоразумения, поэтому они будут называться транспонированными свертками ниже, и рекомендуется не использовать термин деконволюция.
Если мы хотим, чтобы наша сеть изучала лучший метод повышения частоты дискретизации, мы можем использовать транспонированную свертку в это время. Этот метод не использует предопределенные методы интерполяции, у него есть параметры, которые можно узнать. Важно понимать концепцию транспонированной свертки, потому что она была применена в нескольких важных литературах, таких как:
Операция свертки
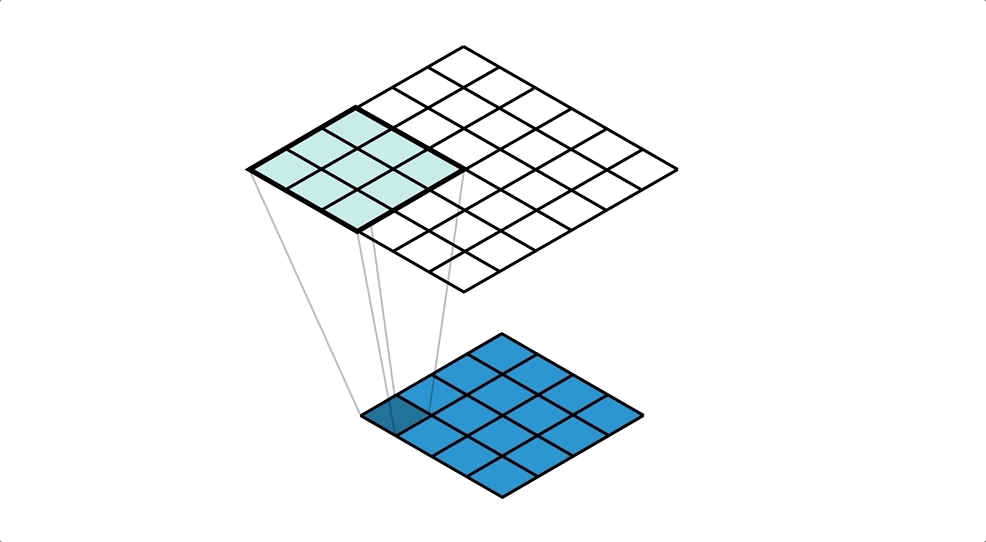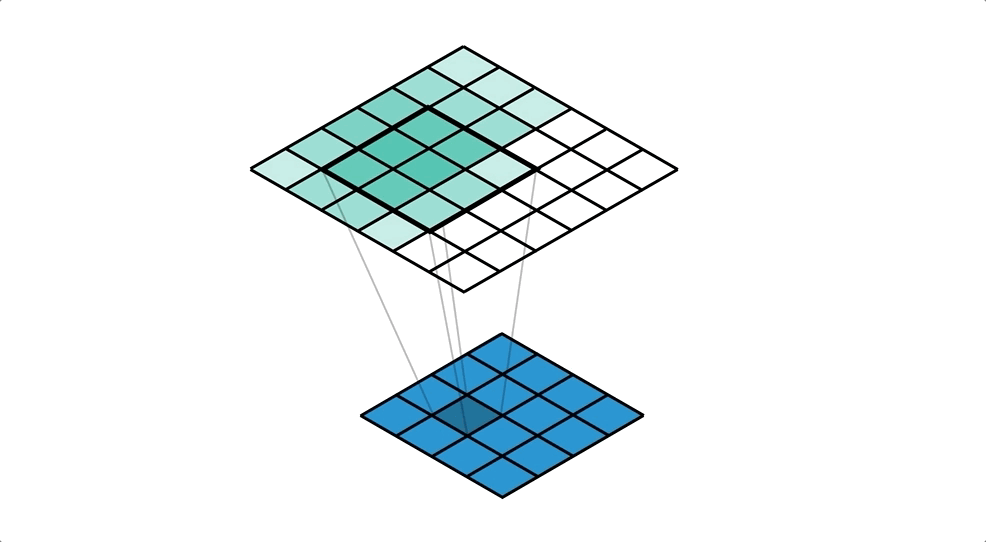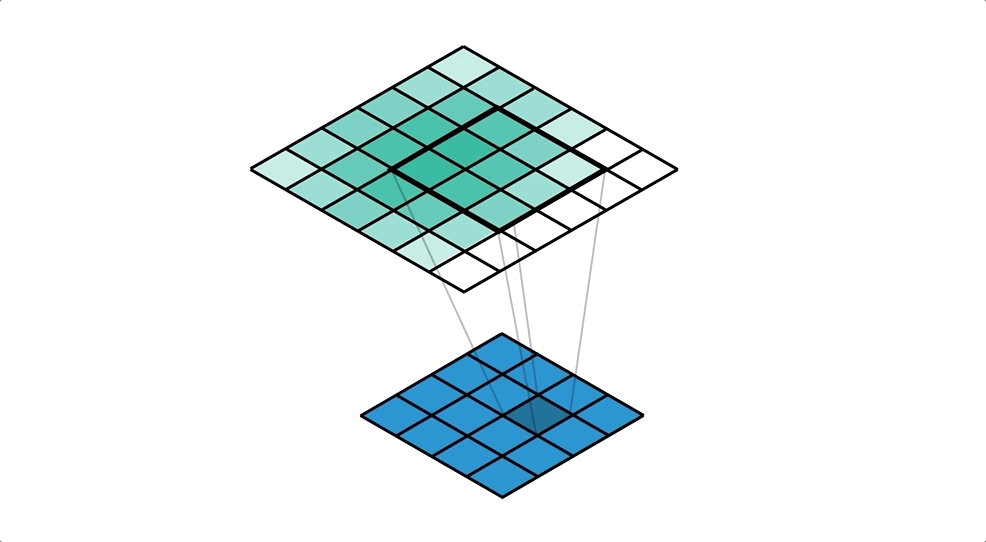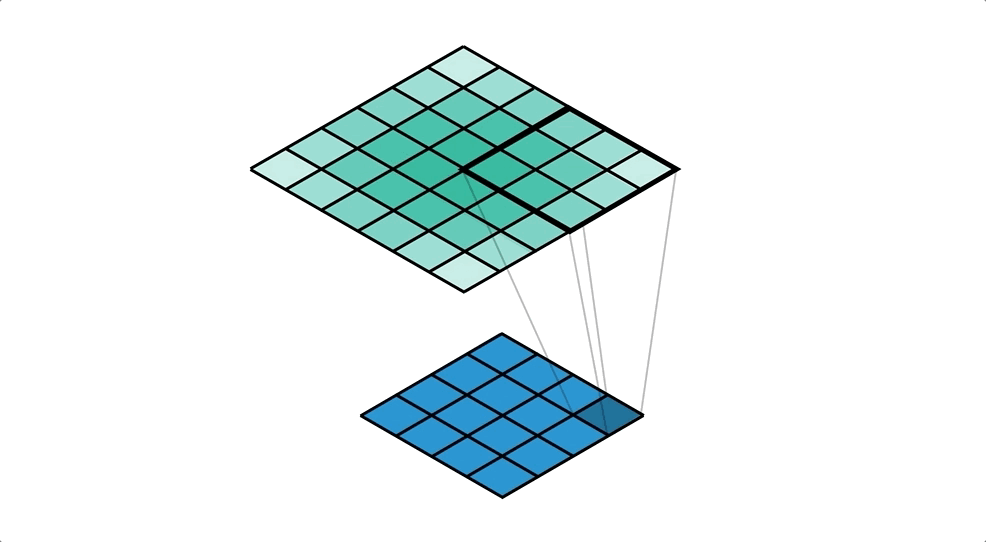
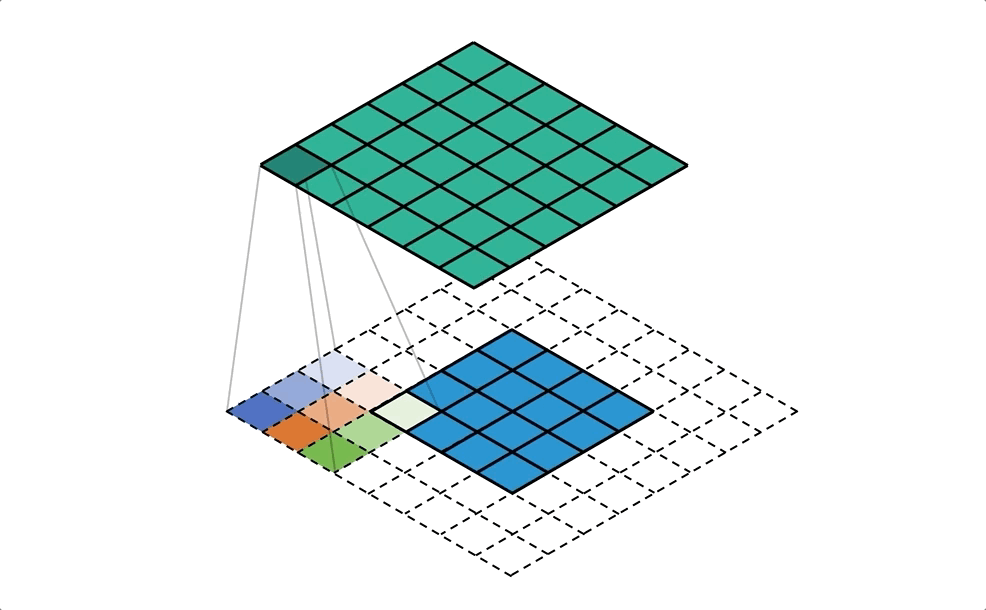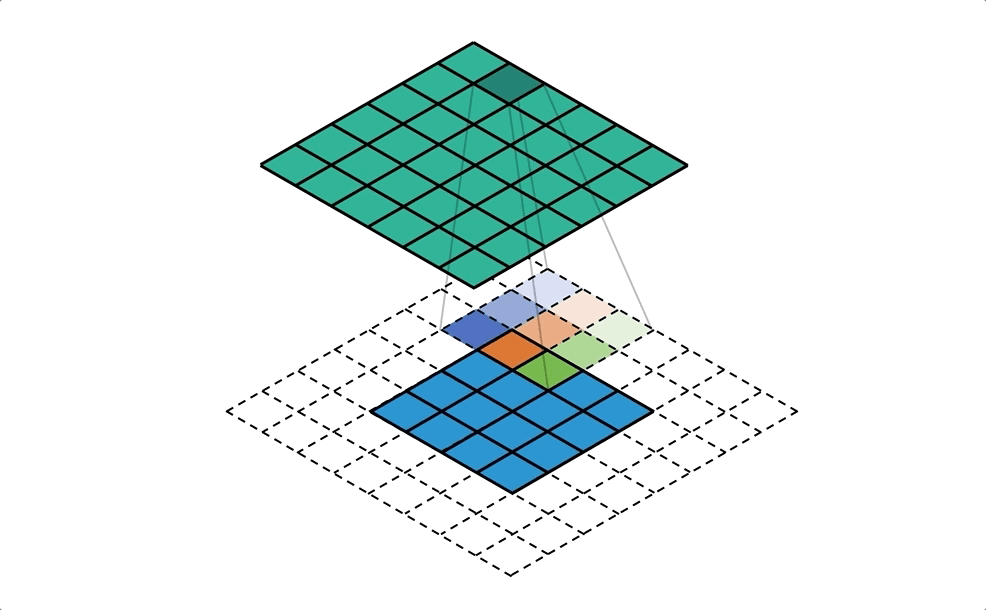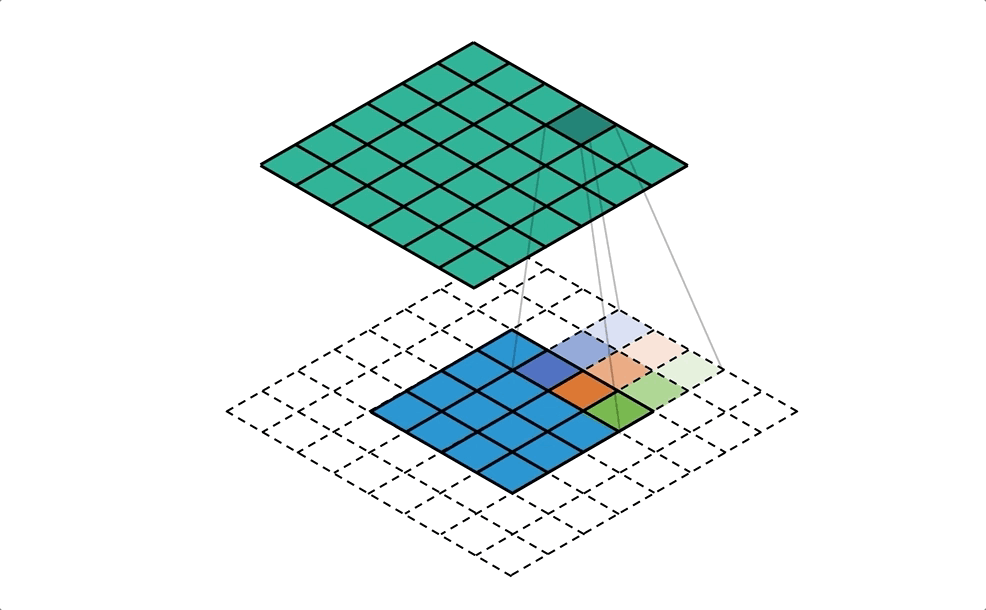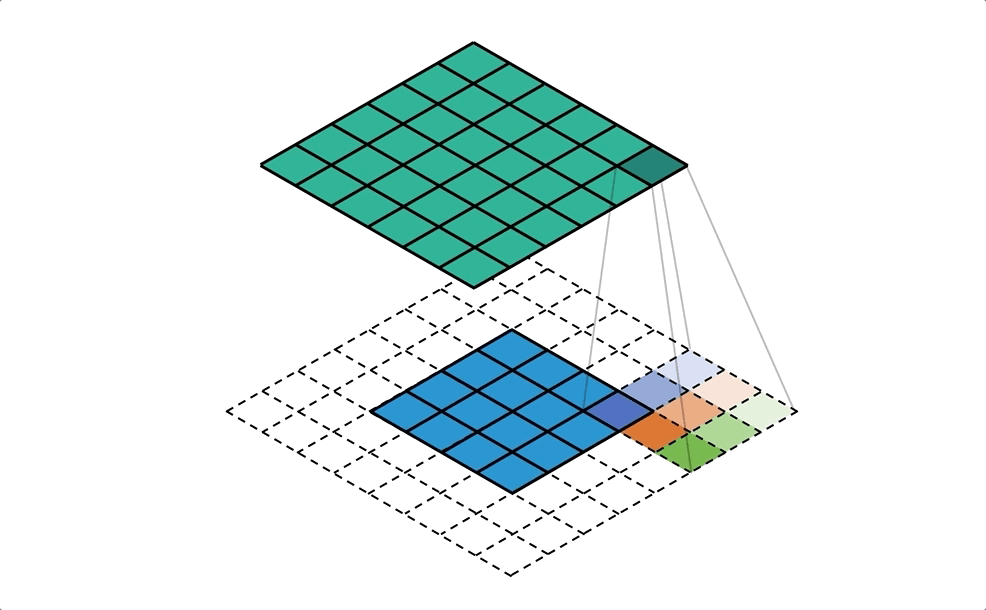
Давайте рассмотрим, как работает операция свертки, и мы будем интуитивно испытывать операцию свертки на небольшом примере. Предположим, у нас есть матрица 4 × 44 × 4. Мы применим к этой матрице ядро свертки 3 × 33 × 3 без добавления каких-либо отступов. Параметр шага устанавливается равным 1, как Как показано на рисунке ниже, вывод представляет собой матрицу 2 × 22 × 2.
Давайте сделаем наоборот
Теперь предположим, что мы хотим отменить операцию. Мы хотим отобразить одно значение во входной матрице на 9 значений в выходной матрице,Это будет отношение отображения один ко многим (один ко многим), Это похоже на обратную операцию операции свертки, основная точка зрения заключается в использовании транспонированной свертки. Например, мы повышаем частоту матрицы 2 × 22 × 2 до матрицы 4 × 44 × 4. Эта операция будет поддерживать соотношение отображения от 1 до 9.

Но как нам это сделать? Для дальнейшего обсуждения нам нужно определить матрицу свертки (convolution matrix) И соответствующая транспонированная матрица свертки (transposed convolution matrix)。
Сверточная матрица
Мы можем представить операцию свертки с матрицей. Это представление очень просто: это не более чем перестановка ядер свертки, чтобы мы могли выполнять операции свертки матриц с использованием обычного умножения матриц. На следующем рисунке показано исходное ядро свертки:

Мы переставили ядро свертки 3 × 33 × 3, чтобы получить следующую матрицу свертки 4 × 164 × 16:
Это матрица свертки, каждая строка которой определяет операцию свертки. Следующий рисунок расскажет вам более интуитивно, как выполняется эта перестановка. Каждая строка матрицы свертки выполняется путем перестановки элементов ядра свертки и добавления заполнения нулями.

Чтобы выразить операцию свертки как векторное умножение матрицы свертки и входной матрицы, мы сведем входную матрицу 4 × 44 × 4 в вектор-столбец с формой 16 × 116 × 1, как показано на рисунке ниже.
Мы можем выполнить матричное умножение этой матрицы свертки 4 × 164 × 16 и вектора входного столбца 1 × 161 × 16, чтобы получить вектор выходного столбца.
Выходная матрица 4 × 14 × 1 может быть преобразована в матрицу 2 × 22 × 2, и эта матрица точно такая же, как та, которую мы получили в ходе традиционной операции свертки в начале.
Проще говоря, эта матрица свертки не имеет ничего, кроме перестановки весов ядра свертки, и тогда операция свертки может быть выражена формой матричного произведения, выраженной в виде вектора столбца матрицы свертки и входной матрицы.
Итак, вы обнаружили, что ключевым моментом является эта матрица свертки, вы можете перейти от 16 (4 × 44 × 4) к 4 (2 × 22 × 2), потому что размер этой матрицы свертки в точности равен 4 × 164 × 16, Затем, если у вас есть матрица 16 × 416 × 4, вы можете перейти от 4 (2 × 22 × 2) к 16 (4 × 44 × 4). Разве это не операция с повышением частоты дискретизации? Aha! Давайте продолжим!
Транспонированная матрица свертки
Мы хотим перейти от 4 (2 × 22 × 2) к 16 (4 × 44 × 4), поэтому мы используем матрицу 16 × 416 × 4, но есть еще одна вещь, которую нужно отметить, мы хотим сохранить 1 До 9 картографических отношений.
Предположим, что мы переносим эту матрицу свертки C (4 × 16) C (4 × 16) в CT (16 × 4) CT (16 × 4). Мы можем умножить матрицу CTCT и вектор столбцов (4 × 1) (4 × 1), чтобы сгенерировать выходную матрицу 16 × 116 × 1. Эта транспонированная матрица отображает элемент на 9 элементов.
Этот вывод может быть сформирован как (4 × 4) (4 × 4) матрица:
Мы просто повышаем частоту малой матрицы (2 × 2) (2 × 2) в большую матрицу (4 × 4) (4 × 4). Эта транспонированная матрица свертки поддерживает отношение отображения от 1 элемента до 9 элементов, поскольку это отношение отражается в ее транспонированном элементе свертки.
Обратите внимание, что: Параметры транспонированной матрицы свертки здесь,Не обязательноЭто получается простым транспонированием исходной матрицы свертки. Операция транспонирования обеспечивает только форму транспонированной матрицы свертки.
резюме
Транспонированная операция свертки устанавливает те же отношения соединения, что и обычная операция свертки, за исключением того, что это соединение начинается с обратного направления. Мы можем использовать его для повышения дискретизации. Кроме того, параметры этой транспонированной матрицы свертки можно узнать, поэтому нам не нужны некоторые заранее определенные методы. Даже если это называется транспонированной сверткой, это не означает, что мы просто транспонируем существующую матрицу свертки и используем ее транспонированное значение.
По сути, транспонированная свертка не является сверткой, но мы можем думать о ней как о свертке и использовать ее как свертку. Мы добавляем, вставляя 0 между элементами во входной матрице, чтобы добиться увеличения размера выборки, и затем с помощью обычной операции свертки можно получить тот же эффект, что и транспонированной свертки. В некоторых статьях вы обнаружите, что все они объясняют транспонированную свертку, но это потому, что ее нужно повысить, добавив 0 перед операцией свертки, поэтому она относительно неэффективна.
Обратите внимание: Транспонированная свертка вызовет артефакты шахматной доски в сгенерированном изображении, эта статья《Deconvolution and Checkerboard Artifacts》Рекомендуется операция повышения дискретизации (то есть операция интерполяции), за которой следует операция свертки, чтобы уменьшить это явление. Если вашей основной целью является создание изображений с минимальным количеством эффектов шахматной доски, то эту статью стоит прочитать.
Transposed Convolutions explained with… MS Excel!
You’ve successfully navigated your way around 1D Convolutions, 2D Convolutions and 3D Convolutions. You’ve conquered multi-input and multi-output channels too. But for the last blog post in the convolution series we’re onto the boss level: understanding the transposed convolution.
So let’s start with the name and see what we’re dealing with. A transpose “causes (two or more things) to change places with each other”. When we’re transposing matrices we change the order of their dimensions, so for a 2D matrix we essentially ‘flip’ values with respect to the diagonal. We won’t be covering this in the series, but it’s possible to represent operations (such as rotations, translations, and convolutions) as matrices. See Section 4.1 of Dumoulin & Visin if you’re interested. When we’re transposing convolutions we change the order of the dimensions in this convolution operation matrix, which has some interesting effects and leads to different behaviours to the regular convolutions we’ve learnt about so far.
Sometimes you’ll see this operation referred to as a ‘deconvolution’ but they are not equivalent. A deconvolution attempts to reverse the effects of a convolution. Although transposed convolutions can be used for this, they are more flexible. Other valid names for transposed convolutions you might see in the wild are ‘fractionally strided convolutions’ and ‘up convolutions’.
Why do we need them?
One of the best ways for us to gain some intuition is by looking at examples from Computer Vision that use the transposed convolution. Most of these examples start with a series of regular convolutions to compress the input data into an abstract spatial representation, and then use transposed convolutions to decompress the abstract representation into something of use.
A convolutional auto-encoder is tasked with recreating its input image, after passing intermediate results through a ‘bottleneck’ of a limited size. Uses of auto-encoders include compression, noise removal, colourisation and in-painting. Success depends on being able to learn dataset specific compression in the convolution kernels and dataset specific decompression in the transposed convolution kernels. Why stop there though?
With ‘super resolution’ the objective is to upscale the input image to higher resolutions, so transposed convolutions can be used as an alternative to classical methods such as bicubic interpolation. Similar arguments to convolutions using learnable kernels over hand crafted kernels apply here.
Semantic segmentation is an example of using transposed convolution layers to decompress the abstract representation into a different domain (from the RGB image input). We output a class for each pixel of the input image, and then just for visualisation purposes, we render each class as a distinct colour (e.g. the person class shown in red, cars in dark blue, etc.).
Any disadvantages?
Clearly transposed convolutions are more flexible than classical upsampling methods (like bicubic or nearest neighbour interpolation), but there are a few disadvantages. You can’t apply transposed convolutions without learning the optimal kernel weights first, as you could with classical upsampling methods. And there can be checkerboard artifacts in the output.
Advanced: to avoid checkerboard artifacts, an alternative upsampling method that’s gaining popularity is to apply classical upsampling followed by a regular convolution (that preserves the spatial dimensions).
A spreadsheet paints a thousand formulas
Unlike for regular convolutions, where explanations are pretty consistent and diagrams are often intuitive, the world of transposed convolutions can be a little more daunting. You’ll often read different (seemingly disconnected) ways to think about the computation. So in this blog post I’ll take two mental models of transposed convolutions and help you join the dots using our trusty friend… MS Excel. And we’ll code things up in Apache MXNet because we’ll probably want to use them in practice some day!
Advanced: the transposed convolution operation is equivalent to the gradient calculation for a regular convolution (i.e. the backward pass of a regular convolution). And vice versa. Consider this while reading the next section.
Mental Model #1: Distributing Values
Our first mental model is more intuitive (at least for me), and we’ll work step-by-step towards the second mental model that’s closer to how transposed convolutions are implemented in deep learning frameworks.
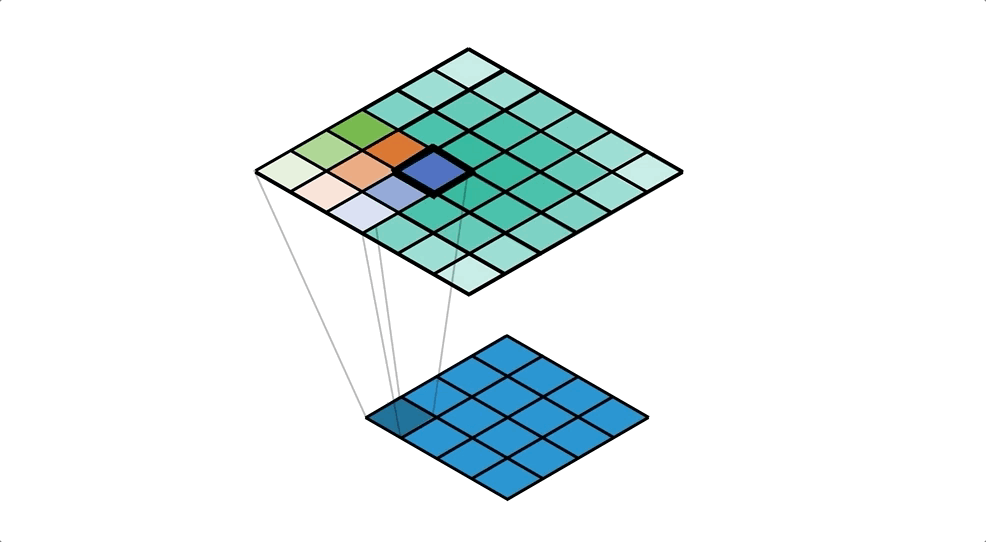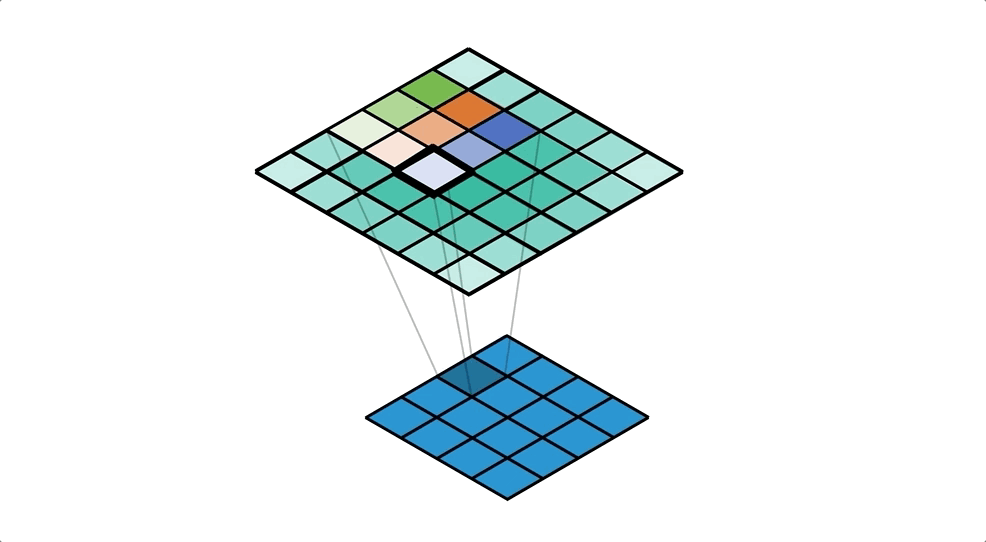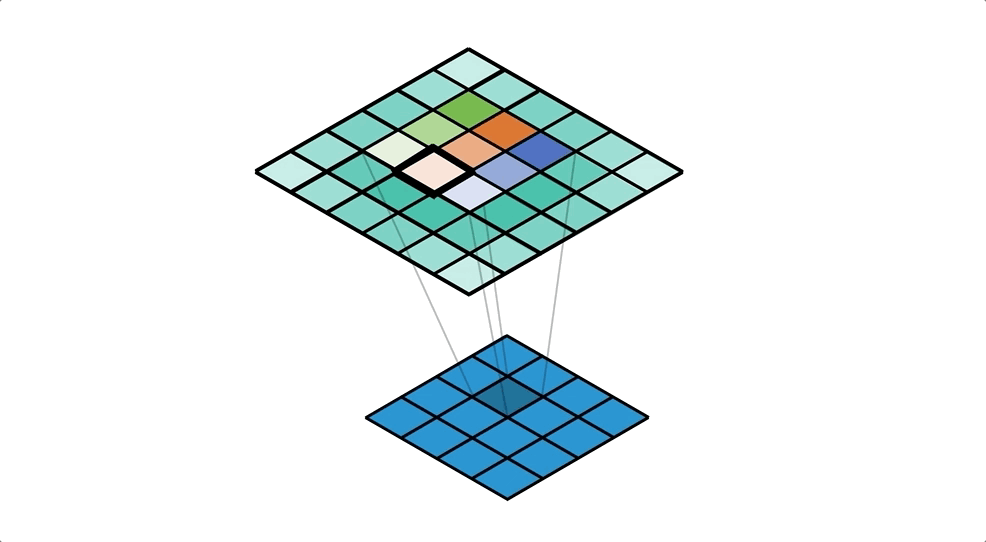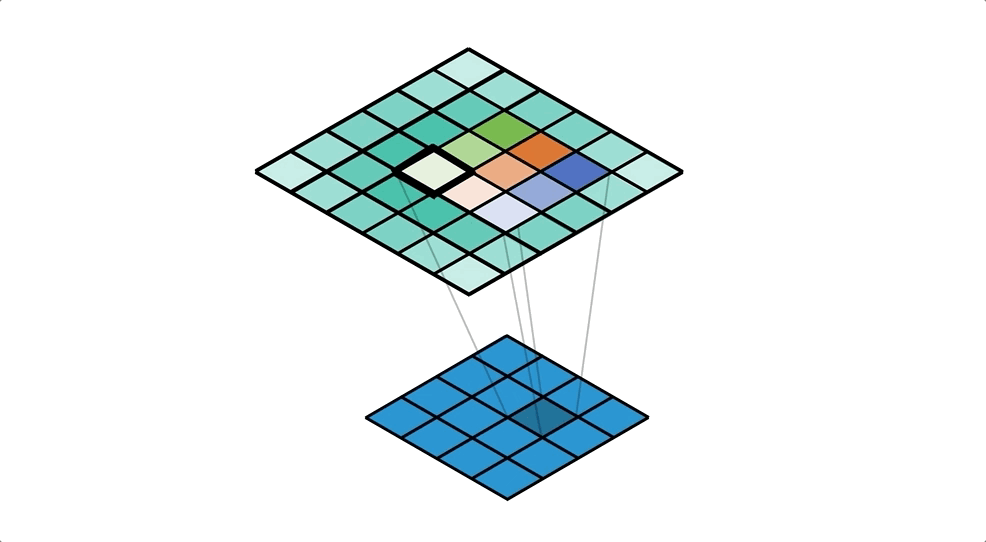
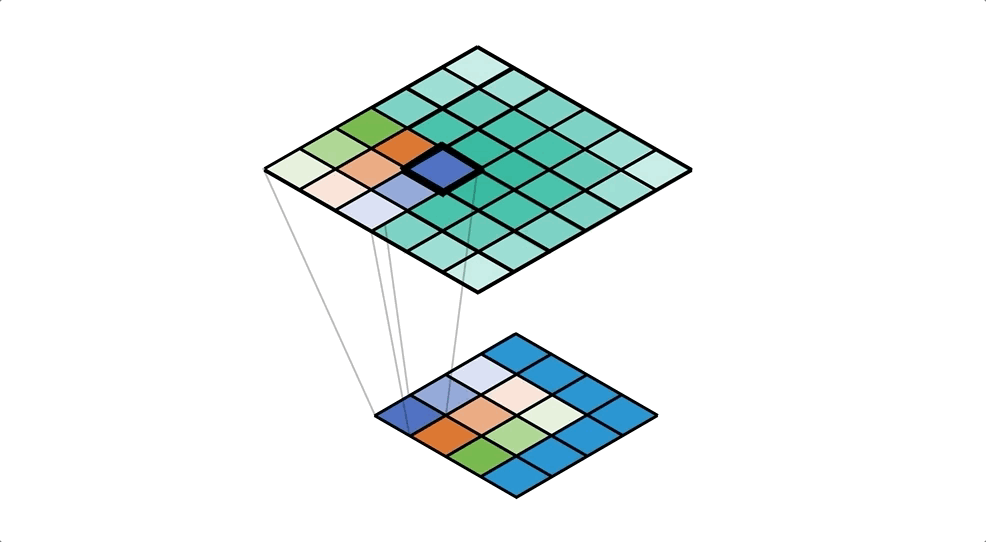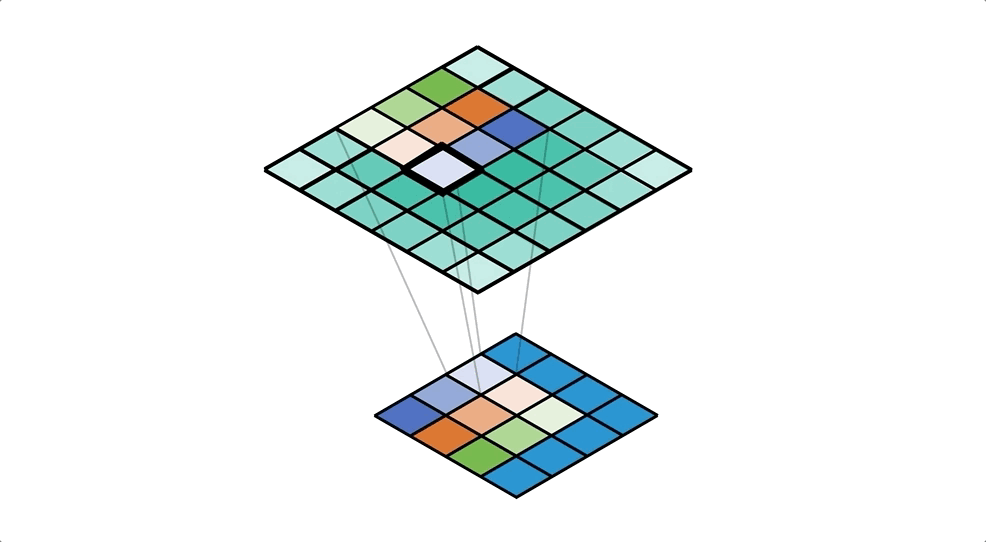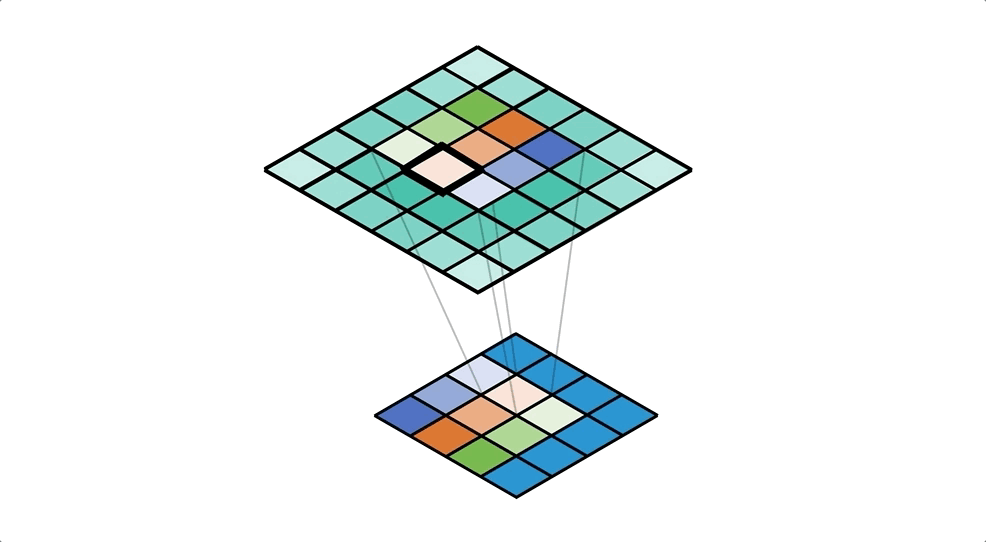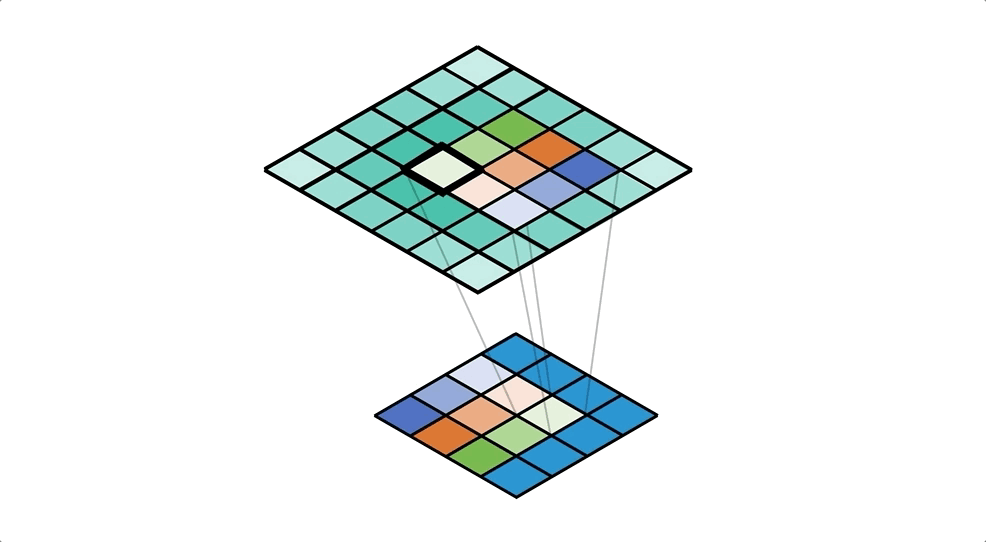
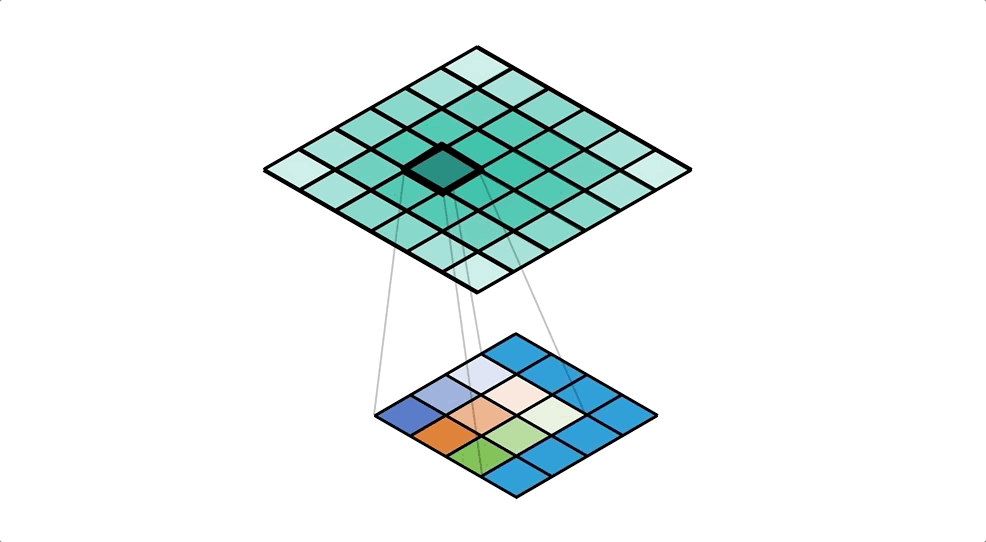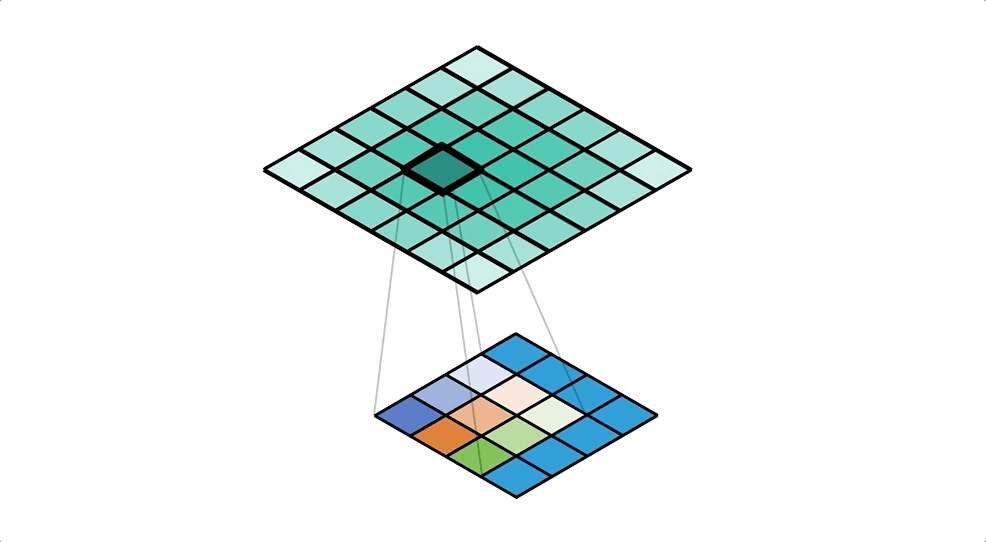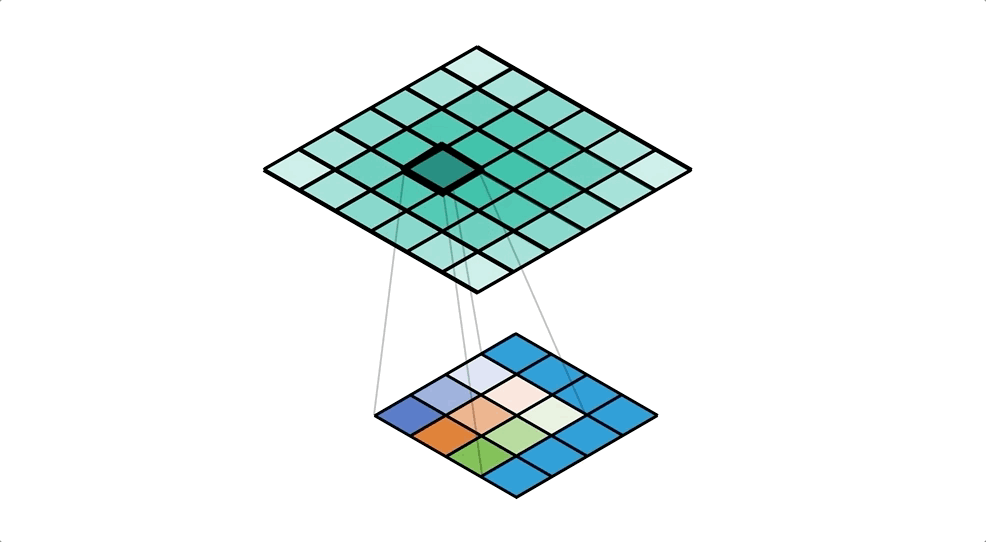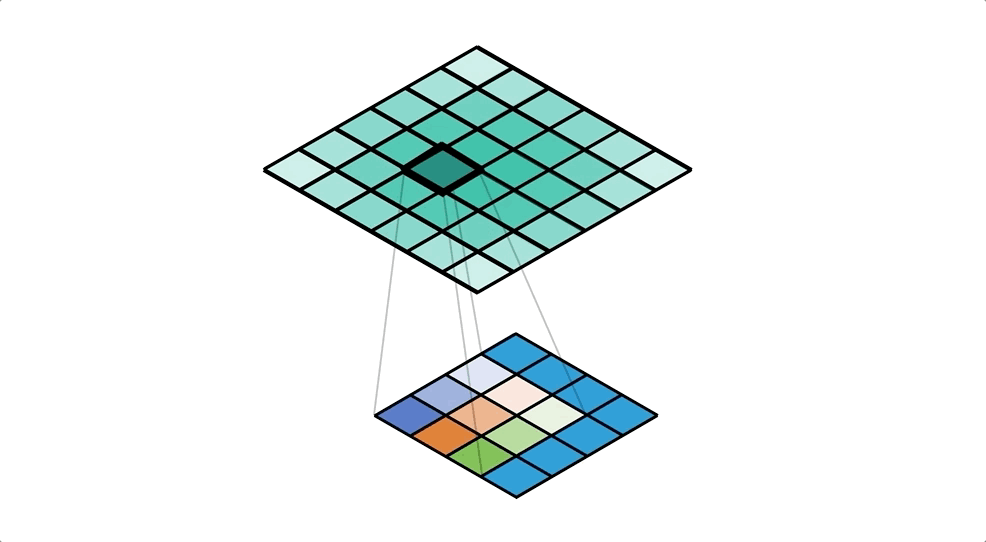
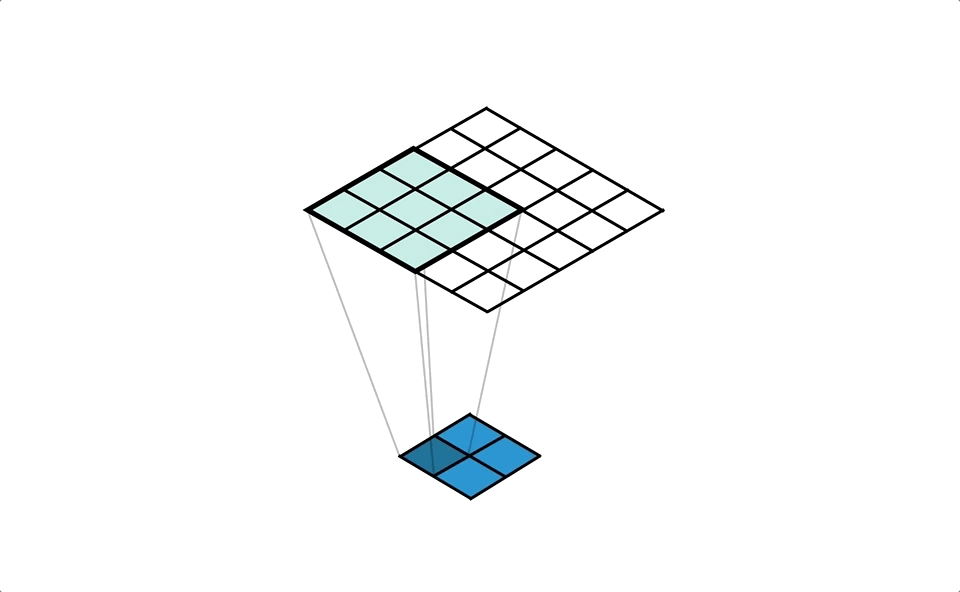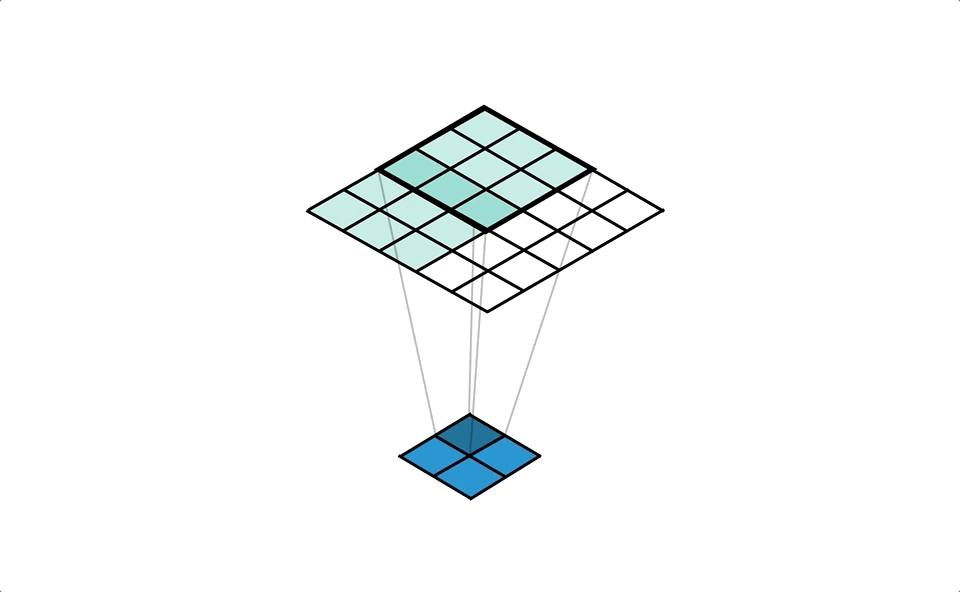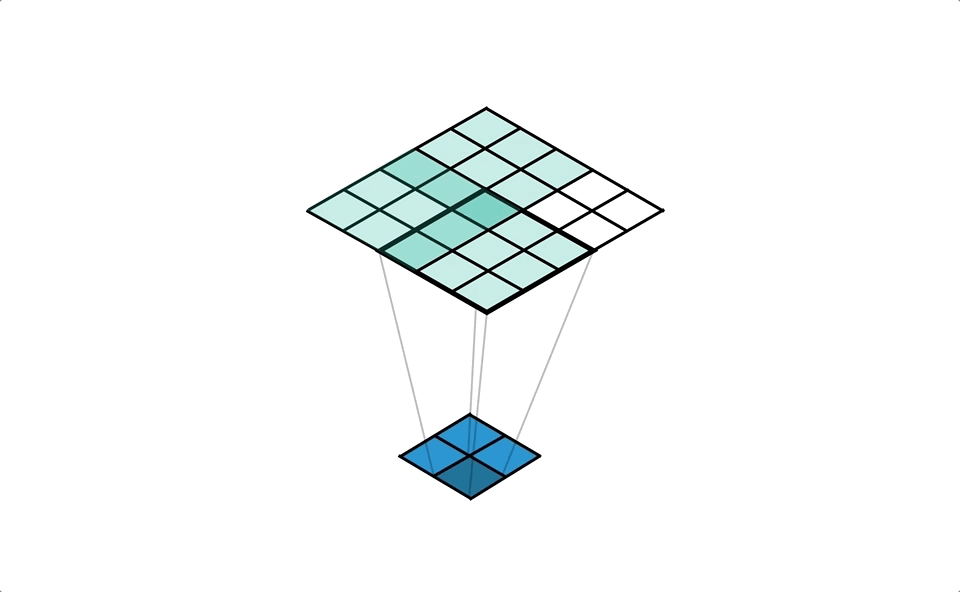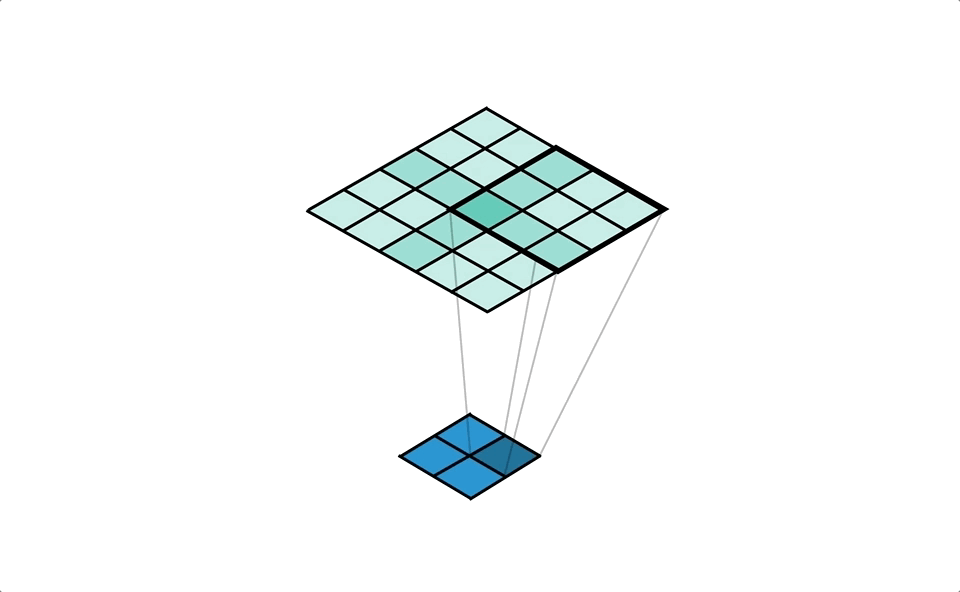
Let’s start from the perspective of a single value in the input. We take this value and ‘distribute’ it to a neighbourhood of points in the output. A kernel defines exactly how we do this, and for each output cell we multiply the input value by the corresponding weight of the kernel. We repeat this process for every value in the input, and accumulate values in each output cell. Check out Figure 4 for an example of this accumulation (with unit input and kernel).
Our kernel values are hidden in the animation above, but it is important to understand that the kernel is defining the amount of the input value that’s being distributed to each of the output cells (in the neighbourhood). We can see this more clearly in the spreadsheet in Figure 5, even with a unit kernel.
Advanced: if you’re observant you may have spotted that the edges of the output get less accumulation than the centre cells. Often this isn’t an issue because kernel weights learn to adjust for this and can be negative too.
Mental Model #2: Collecting Values
Another way of thinking about transposed convolutions is from the perspective of a cell in the output, rather than a value in the input as we did with first mental model. When we do this we end up with something strangely familiar, something very similar to a regular convolution!
One step at a time we’ll convert what we already know to this new way of thinking. We start with the animation in Figure 6. It highlights a single cell in the output, and looks at the input values that distribute into it. You should pay close attention to the kernel weights used for each of the input values.
We can make this even more obvious in Figure 7 by colour coding the input values by the kernel weight that they get multiplied with before the accumulation. You should notice how the kernel on the input has ‘flipped’ about the centre; i.e. the dark blue weight of the kernel was bottom right when distributing, but it’s moved to top left when we think about collecting.
We’ve just created a convolution! Check the freeze frame in Figure 8 if you don’t believe me. We’re using the ‘flipped’ kernel, that despite the name, ‘transposed convolution’, isn’t actually a transpose of the distribution kernel.
Collecting values with 2D Convolutions allows us to write explicit formulas for the output: ideal for MS Excel and also code implementations too. So we’d have the following formula for the top left cell of the output:
We can confirm our results with the Apache MXNet code seen previously:
GNIDDAP!
We’ve just seen a strange example of a Conv2DTranspose with no padding (appearing to have padding of 2×2 when thinking about it as a Conv2D ) but things get even more mysterious when we start adding padding.
With regular convolutions, padding is applied to the input which has the effect of increasing the size of the output. With transposed convolutions, padding has the reverse effect and it decreases the size of the output. So I’m coining ‘gniddap’ in the hope you’ll remember the reverse ‘padding’.
We can think about padding for transposed convolutions as the amount of padding that’s included in the complete output. Sticking with our usual example (where the complete output is 6×6), when we define padding of 2×2 we’re essentially saying that we don’t care about the outer cells of the output (with width of 2) because that was just padding, leaving us with a 2×2 output. When thinking about transposed convolutions as regular convolutions we remove padding from the input by the defined amount. See Figure 11 for an example with MS Excel, and notice how the outputs are identical to the central values of the output in Figure 10 when there was no padding.
SEDIRTS!
Strides are also reversed. With regular convolution we stride over the input, resulting in a smaller output. But when thinking about transposed convolutions from a distribution perspective, we stride over the output, which increases the size of the output. Strides are responsible for the upscaling effect of transposed convolutions. See Figure 12.
Advanced: checkerboard artifacts can be seen in the example below, which can start to become an issue when using strides (even after stacking multiple layers).
Although things are clear from the distributional perspective above, things get a little strange when we think about things from a collection perspective and try to implement this using a convolution. Stride over the output is equivalent to a ‘fractional stride’ over the input, and this is where the alternative name for transposed convolutions called ‘fractionally strided convolutions’ comes from. A stride of 2 over the output would be equivalent to a stride of 1/2 over the input: a fractional stride. We implement this by introducing empty spaces between our input values, the amount proportional to the stride, and then stride by one. As a result we’re applying the kernel to a region of the input that’s smaller than the kernel itself! See Figure 13 for an example.
Multi-Channel Transposed Convolutions
As with regular convolutions, each input channel will use a separate kernel and the results for each channel will be summed together to give a single output channel. We repeat this process for every output channel required, using a different set of kernels. All these kernels are kept in a single kernel array with shape:
(input channels, output channels, kernel height, kernel width)
Which is different from the kernel array shape used for a regular convolution:
(output channels, input channels, kernel height, kernel width)
Get experimental
All the examples shown in this blog posts can be found in this Excel Spreadsheet (and Google Sheet too). Click on the cells of the output to inspect the formulas and try different kernel values to change the outputs. After replicating your results in MXNet Gluon, I think you can officially add ‘convolution wizard’ as a title on your LinkedIn profile!
Congratulations!
You’ve made it to the end of this excellent series on convolutions. I hope you learnt something useful, and now feel ready to apply these techniques to real world problems with Apache MXNet. Any questions? Just drop a comment below or check out the MXNet Discussion forum. Shares and claps would also be greatly appreciated. Many thanks!
Understanding transposed convolutions
Last Updated on 30 March 2021
Recently, we’ve looked at convolutional layers and certain variations to see how they can be used in machine learning problems. Today, we’ll focus on a variant called transposed convolution, which can be used for upsampling images (making them larger) or finding the original representation of a convolutional filter map.
We’ll first cover a normal convolution before we introduce transposed ones. We do so by means of the convolution matrix. Hope you’ll enjoy!
After reading this tutorial, you will understand…
Update 09/Feb/2021: ensure that article is up to date.
Update 01/Mar/2020: adapted images for the “normal convolution” to make them equal to the convolution matrix example.
Table of contents
Summary: understanding transposed convolutions
Convolutional Neural Networks are used for computer vision projects and can be used to automatically extract features from inputs like photos and videos. These neural networks employ so-called convolutional layers that convolve (slide) over the input image, try to detect patterns, and adapt weights accordingly during the training process – allowing learning to occur.
Sometimes, however, you want the opposite to happen: invert the output of a convolutional layer and reconstruct the original input. This is for example the case with autoencoders, where you use normal convolutions to learn an encoded state and subsequently decode them into the original inputs. If done successfully, the encoded state can be used as a lower-dimensional representation of your input data, for dimensionality reduction.
Transposed convolutional layers can be used for this purpose. Rather than performing interpolation, they learn a set of weights that can be used to reconstruct original inputs. They can be trained jointly with convolutional layers during the training process. In this article, we’ll cover transposed convolutions in more detail. We’ll show you how they work and how they are applied.
What does a normal convolution do?
If we wish to understand transposed convolutions, we must be able to compare them with something – and that something, in our case, is a normal convolution.
More specifically, we’re looking at a convolution of a one-channel image: this is likely a grayscale image. Normally, you would convolve over multiple channels, and you would likely use multiple kernels. For the sake of simplicity, our image has one channel and we use N = 1 kernels.
It must now follow why the 2×2 kernel produces a 2×2 output when convolving over a 3×3 image. I’ll briefly recap it next.
When the convolution process starts, the kernel is placed at the upper left corner. It performs element-wise multiplications and hence, produces a scalar output (a number) for the overlapping area. It then moves one step to the right, performs the same thing, but then cannot move any further to the right.
Let’s pause for a second! 👩💻
Blogs at MachineCurve teach Machine Learning for Developers. Sign up to MachineCurve’s free Machine Learning update today! You will learn new things and better understand concepts you already know.
We send emails at least every Friday. Welcome!
It then simply moves one down, if possible, and does the same trick again. Once it can no longer go to the right, it will attempt to move one down, but cannot do so for the simple reason that we’ve already reached the end of the image. The convolution operation then stops. Note that in the first row, two scalar values were produced, as well as in the second row. These two times two scalar values produce the 2×2 output displayed in the image above.
Note that we assume a stride of 1 in this example.
If you wish to understand normal convolutions in more detail, I suggest that you take a look at this post before moving on.
The goal: reconstructing the original input
Now what if your goal is to do the opposite: given a summary, i.e. the result of the convolution, reconstructing the original input?
We call this “upsampling”.
You have multiple options.
Traditional interpolation techniques
First and foremost, it is possible to use traditional interpolation techniques to make your image larger. For example, you could use bicubic or bilinear interpolation to achieve the result you’re interested in. However, they’re not too flexible: they simply compute an estimate of the interpolated pixel values based on their surroundings. In the case of making images larger without losing a sense of detail, we might be interested in a different approach – one where the means of interpolation is learnt based on the target data. Regular and transposed convolutions then enter the spotlight.
Regular convolutions – or not?
First, as described more lengthily in Dumoulin & Francesco (2016), you can employ a regular convolution operation. This, however, might not be the most efficient route towards reconstructing the original image:
Finally note that it is always possible to emulate a transposed convolution with a direct convolution. The disadvantage is that it usually involves adding many columns and rows of zeros to the input, resulting in a much less efficient implementation.
Dumoulin & Francesco (2016)
(note that the paper gives many examples – it’s a good recommendation if you wish to understand it in even greater detail!)
Let’s now look at our third possible approach: a transposed convolution.
Transposed Convolution
Rather, we must find another way of doing so. Enter the transposed convolution. We’ll discuss this way of working next in a multi-stage fashion. Firstly, we describe how forward and backwards passes are normally covered by a convolutional layer and how they are inverted in a transposed convolution.
Secondly, we represent the normal convolution with a Convolution Matrix – it’s the first step to demonstrating the power of a transposed convolution. Additionally, we’ll compute the normal convolution output based on this matrix to demonstrate that we’ll achieve the same result.
Subsequently, we’ll introduce the transposed convolution based on the Convolution Matrix we defined earlier, and show that it’s indeed possible to reconstruct the original input.
Never miss new Machine Learning articles ✅
Blogs at MachineCurve teach Machine Learning for Developers. Sign up to MachineCurve’s free Machine Learning update today! You will learn new things and better understand concepts you already know.
We send emails at least every Friday. Welcome!
Representing the normal convolution with a Convolution Matrix
Let’s now see how we can represent the normal convolution by means of a Convolution Matrix. We can use this matrix to demonstrate how the Transposed Convolution works (Dumoulin & Visin, 2016).
Suppose that we’re performing convolutions with a 2×2 kernel on a 3×3 input image, like this:
With our understanding of how regular convolutions work, it’s not surprising to find that we’ll end up with a 2×2 output or feature map:
We can also represent this operation as a Convolution Matrix.
What is a convolution matrix?
It’s a matrix which demonstrates all positions of the kernel on the original image, like this:
One who looks closely, will notice that each row represents a position of the kernel on top of the image: in the first row, for example, the kernel is positioned at the top left of the image. The <1, 2, 0>at the first row of the convolution matrix therefore represents the effect of the convolution at the first row of the input image. The <2, 1, 0>represents the effect of the convolution at the second row of the input image. Since at this point in time, the convolution is not applied in either the 3rd column or the 3rd row, either the third column value of the first and second row and all the third row values are 0.
Note that when the kernel moves to the right in the second iteration, the current position is represented by the second row of the convolution matrix, and so on. The convolution matrix therefore describes the full convolutional operation of the kernel on the input image.
Computing the normal convolution output with a Convolution Matrix
The convolution matrix can be used to compute the output of a normal convolution. Doing so is really simple, namely, by flattening the input image into a (9×1) feature vector:
It’s possible to represent the 3 x 3 image as an 1 x 9 image instead, which essentially allows you to contain the same amount of data in the same ordering – by breaking the 1 x 9 image apart after each 3rd block and stacking the 1 x 3 blocks together, you’ll arrive at the 3 x 3 image again.
The fun thing is that we can multiply this (9×1) matrix with the (4×9) convolution matrix and hence achieve a (4×9) x (9×1) = (4×1) output:
When turning it around, breaking it into blocks of two and stacking them vertically, we see that it’s the same as what we saw earlier:
We can thus express the convolutional operation by means of a convolution matrix!
From output back to the input: the Transposed Convolution
Now suppose that this is your input:
While this is your desired output:
Join hundreds of other learners! 😎
Blogs at MachineCurve teach Machine Learning for Developers. Sign up to MachineCurve’s free Machine Learning update today! You will learn new things and better understand concepts you already know.
We send emails at least every Friday. Welcome!
Or, in other words: you’re trying to do the opposite – going backwards from a summarized version of the original input to the original input, rather than creating the summary.
We’ll now find why we call the type of convolution transposed, as we can also represent this by means of the convolution matrix – although not the original one, but its transpose:
a.k.a. the one where the columns have become rows and vice-versa.
The input can also be represented as follows:
You may now have noticed that once again, we’re in a situation in which we can perform a matrix multiplication: we now have a (9×4) matrix and a (4×1) matrix, which we can multiply to arrive at a (9×1) matrix or, when broken apart, the (3×3) matrix we were looking for!
Implementations in deep learning frameworks: normal convolution, transposed matrix
There are effectively two ways of implementing the transposed convolution (Theano, n.d.):
Frameworks such as TensorFlow and Theano implement transposed convolutions in this way or by using a very similar one.
Learnable kernels are what make Transposed convolutions different
Now, one may wonder:
Why should I use transposed convolutions rather than traditional interpolation techniques?
Although this is slightly dependent on why you intend to use such convolutions, there may be very good reasons for doing so.
Note that in both the regular convolution matrix and the transposed one, the non-zero fields are determined by the kernel.
And the kernel is learnt over time, as during model optimization they are adapted continuously to better reflect the relationships underlying your dataset.
What this means is that, contrary to regular interpolation techniques, you can learn kernels first (e.g. by applying regular convolution operations on your data), and subsequently using them to define your transposed convolution, in order to find your original data – or at least, something that hopefully looks like it.
This, in itself, allows one to use them for very interesting applications.
Applications of transposed convolutions
Firstly, it is of course possible to perform upsampling operations with transposed convolutions. That is, when you have a smaller image, you can make it larger by applying transposed convolutions. Note that you’ll have to learn the weights in order to do so – which might mean that you’re better off with traditional interpolation if you want fast results.
We help you with Machine Learning! 🧠
Blogs at MachineCurve teach Machine Learning for Developers. Sign up to MachineCurve’s free Machine Learning update today! You will learn new things and better understand concepts you already know.
We send emails at least every Friday. Welcome!
Secondly, transposed convolutions can be used in Generative Adversarial Networks (Shibuya, 2019). Those networks randomly generate a small matrix and use fractionally-strided convolutions (another name to describe transposed convolutions, but then perhaps in the relatively inefficient implementation of regular convolutions with fractional strides) to upsample them to true images. The weights that have been learnt in the process allow for the upsampling of the random noise to the actual image.
Thirdly, they’re also used in segmantic segmentation, where you wish to classify each pixel of an image into a certain category (Shibuya, 2019). They work by generating predictions for intermediate results achieved with convolutions, subsequently upsamling those to find predictions for the originally-shaped input image.
Finally, and perhaps more recently, they are used in what is called a convolutional autoencoder. In those, convolutional layers are used to find an encoding for some input, i.e. a representation of the original input in much lower dimensionality. A clear example would be a radar image with a landmine and one without a landmine; for the latter, one could train an autoencoder to find a particular encoding. However, autoencoders also contain a decoding side: given some encoded input, it attempts to find the original output (by, unsurprisingly, upsampling layers such as transposed convolutions). By comparing the original input image with the output image, it’s possible to identify whether the input belongs to a certain class. In our case, that would be landmine yes/no, and ‘yes’ would only be the case if the decoded encoding really looks like the original image, since then the landmine-trained encoding worked well.
Summary
In this blog, we’ve seen how transposed convolutions work and what they can be used for. We’ve looked at convolution matrices that can be used for upsampling and demonstrated how both the regular convolution matrix and the transposed one are defined by the kernels that can be learnt. Interesting application areas are upsampling, GANs, semantic segmentation and autoencoders.
Thank you for reading! I hope this blog has made things a bit more clear 🙂 Would you kindly let me know in the comments? 👇 If not – or if you have questions or remarks – please feel free to write a comment as well! I’m more than happy to reply. Should I’ve made a mistake, which can happen, I’ll gladly adapt my blog and note you as a contributor. Thank you!