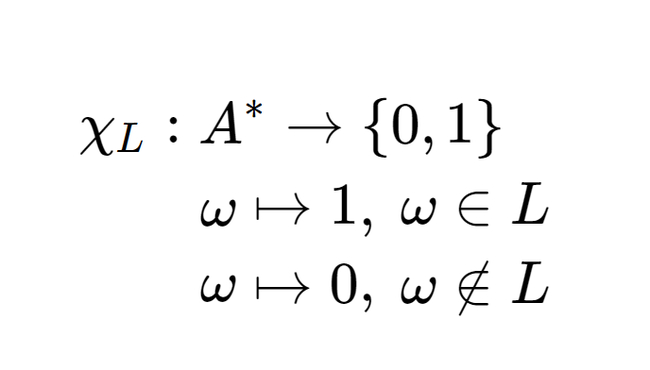что зачем почему перельман
 drumsmen
drumsmen
ПУСТЬ ВРЕМЯ ВАШИХ ПЕРЕМЕН РАБОТАЕТ НА ВАС!
«Задача тысячелетия», решенная российским математическим гением, имеет отношение к происхождению Вселенной. Понять суть загадки дано не каждому математику…
ИГРА РАЗУМА
Еще недавно математика не сулила ни славы, ни богатства своим «жрецам». Им даже Нобелевскую премию не давали. Нет такой номинации. Ведь, по весьма популярной легенде, жена Нобеля однажды изменила ему с математиком. И в отместку богач лишил всю их крючкотворную братию своего уважения и призовых денег.
Ситуация изменилась в 2000 году. Частный математический Институт Клэя (Clay Mathematics Institute) выбрал семь наиболее трудных задач и пообещал за решение каждой платить по миллиону долларов.
На математиков посмотрели с уважением. В 2001 году на экраны даже вышел фильм «Игры разума», главным героем которого стал математик.
Топология важна для математической физики, поскольку позволяет понять свойства пространства. Или оценить его, не имея возможности взглянуть на форму этого пространства со стороны. Например, на нашу Вселенную.
Как написал в своей популярной книге другой российский математик, Владимир Успенский, «в отличие от двухмерных сфер трехмерные сферы недоступны нашему непосредственному наблюдению, и нам представить себе их так же трудно, как Василию Ивановичу из известного анекдота квадратный трехчлен».
Жюль Анри Пуанкаре предположил такое в 1904 году. Теперь Перельман убедил всех понимающих, что французский тополог был прав. И превратил его гипотезу в теорему.
Доказательство помогает понять, какая форма у нашей Вселенной. И позволяет весьма обоснованно предположить, что она и есть та самая трехмерная сфера.
Гениальный математик из Санкт-Петербурга Григорий Перельман, прославившийся на весь мир доказательством гипотезы Пуанкаре, наконец, объяснил свой отказ от присужденной за это премии в миллион долларов. Как утверждает «Комсомольская правда», ученый-затворник раскрылся в беседе с журналистом и продюсером кинокомпании «Президент-фильм», которая с согласия Перельмана будет снимать о нем художественную ленту «Формула Вселенной».
Пообщаться с великим математиком посчастливилось Александру Забровскому — он несколько лет назад уехал из Москвы в Израиль и догадался связаться сначала с мамой Григория Яковлевича через еврейскую общину Петербурга, оказав ей помощь. Она поговорила с сыном, и после ее хорошей характеристики тот согласился на встречу. Это поистине можно назвать достижением — журналистам не удавалось «поймать» ученого, хотя они сутками просиживали у его подъезда.
Как рассказал газете Забровский, Перельман произвел впечатление «абсолютно вменяемого, здорового, адекватного и нормального человека»: «Реалистичный, прагматичный и здравомыслящий, но не лишенный сентиментальности и азарта… Все, что ему приписали в прессе, будто он «не в себе», — полная чушь! Он твердо знает, чего хочет, и знает, как добиться цели».
Фильм, ради которого математик пошел на контакт и согласился помогать, будет не о нем самом, а о сотрудничестве и противоборстве трех основных мировых математических школ: российской, китайской и американской, наиболее продвинувшихся по стезе изучения и управления Вселенной.
На вопрос, почему Перельман отказался от миллиона, он ответил:
«Я знаю, как управлять Вселенной. И скажите — зачем же мне бежать за миллионом?»
Забровский разрешил изданию опубликовать фрагмент интервью с ученым, взятого на скамейке в сквере напротив Мариинского театра.
Ученого обижает, как его называют в российской прессе
Перельман объяснил, что не общается с журналистами, потому что тех занимает не наука, а вопросы личного и бытового характера — начиная с причин отказа от миллиона и заканчивая вопросом о стрижке волос и ногтей.
Конкретно с российскими СМИ он не хочет контактировать еще и из-за неуважительного к нему отношения. Например, в прессе его называют Гришей, и такая фамильярность обижает.
Григорий Перельман рассказал, что еще со школьных лет привык что называется «тренировать мозг». Вспоминая, как, будучи «делегатом» от СССР получил золотую медаль на математической олимпиаде в Будапеште, он сказал: «Мы пытались решать задачи, где непременным условием было умение абстрактно мыслить.
В этом отвлечении от математической логики и был главный смысл ежедневных тренировок. Чтобы найти правильное решение, необходимо было представить себе «кусочек мира».
В качестве примера такой «труднорешаемой» задачи он привел такую: «Помните библейскую легенду о том, как Иисус Христос ходил по воде, аки посуху. Так вот мне нужно было рассчитать, с какой скоростью он должен был двигаться по водам, чтобы не провалиться».
С тех пор всю свою деятельность Перельман посвятил исследованию проблемы изучения свойств трехмерного пространства Вселенной: «Это очень интересно. Я пытаюсь объять необъятное. Только ведь любое необъятное тоже объятно», — рассуждает он.
Диссертацию ученый писал под руководством академика Александрова. «Тема была несложной: «Седловидные поверхности в евклидовой геометрии». Можете представить себе в бесконечности равновеликие и неравномерно удаленные друг от друга поверхности? Нам нужно измерить «впадины» между ними», — пояснил математик.
Что значит открытие Перельмана, пугающее спецслужбы мира
«Формулой Вселенной» утверждение Пуанкаре называют из-за его важности в изучении сложных физических процессов в теории мироздания и из-за того, что оно дает ответ на вопрос о форме Вселенной. Сыграет это доказательство большую роль в развитии нанотехнологий».
«Я научился вычислять пустоты, вместе с моими коллегами мы познаем механизмы заполнения социальных и экономических «пустот», — сказал он. — Пустоты есть везде. Их можно вычислять, и это дает большие возможности…
Как пишет издание, масштаб того, что открыл Григорий Яковлевич, фактически шагающий впереди сегодняшней мировой науки, сделало его объектом постоянного интереса спецслужб, не только российских, но и зарубежных.
Он постиг некие сверхзнания, помогающие понять мироздание. И тут возникают вопросы такого рода: «А что будет, если его знания найдут практическое воплощение?»
По сути, спецслужбам нужно знать — представляет ли собой Перельман, а точнее, его знания, угрозу для человечества? Ведь если с помощью его знаний можно свернуть Вселенную в точку, а потом ее развернуть, то мы можем погибнуть либо возродиться в ином качестве? И тогда мы ли это будем? И нужно ли нам вообще управлять Вселенной?
А В ЭТО ВРЕМЯ
Мама гения: «Не задавайте нам вопросов о деньгах!»
Когда стало известно, что математику присудили «Премию тысячелетия», перед его дверью собралась толпа журналистов. Все хотели лично поздравить Перельмана и узнать, возьмет ли он свой законный миллион.
Мы долго стучали в хлипкую дверь (вот бы на премиальные деньги заменить ее), однако математик не открыл. Зато его мать вполне доходчиво расставила все точки над «i» прямо из прихожей.
Люди, живущие в этом же подъезде, очень удивлялись, увидев внезапный интерес к Перельману.
Говорят, накануне математик был замечен с полными пакетами продуктов из магазина. Готовился «держать осаду» вместе с мамой. В прошлый раз, когда в прессе началась шумиха по поводу премии, Перельман не выходил из квартиры три недели.
КСТАТИ
За что еще дадут миллион долларов…
В 1998 году на средства миллиардера Лэндона Клея (Landon T. Clay) в Кембридже (США) был основан Математический институт его имени (Clay Mathematics Institute) для популяризации математики. 24 мая 2000 года эксперты института выбрали семь самых, по их мнению, головоломных проблем. И назначили по миллиону долларов за каждую.
1. Проблема Кука
2. Гипотеза Римана
3. Гипотеза Берча и Свиннертон-Дайера
Проблема связана с решением уравнений с тремя неизвестными, возведенными в степени. Нужно придумать, как их решать, независимо от сложности.
4. Гипотеза Ходжа
В ХХ веке математики открыли метод исследования формы сложных объектов. Идея в том, чтобы использовать вместо самого объекта простые «кирпичики», которые склеиваются между собой и образуют его подобие. Нужно доказать, что такое допустимо всегда.
5. Уравнения Навье – Стокса
О них стоит вспомнить в самолете. Уравнения описывают воздушные потоки, которые удерживают его в воздухе. Сейчас уравнения решают приблизительно, по приблизительным формулам. Нужно найти точные и доказать, что в трехмерном пространстве существует решение уравнений, которое всегда верно.
6. Уравнения Янга – Миллса
Новое в блогах
Григорий Перельман: Я знаю, как управлять Вселенной. Зачем же мне бежать за миллионом?
Фрагменты интервью
— Григорий Яковлевич, еще школьником вы представляли СССР на математической олимпиаде в Будапеште. И взяли золотую медаль…
— Готовясь к олимпиаде, мы пытались решать задачи, где непременным условием было умение абстрактно мыслить. В этом отвлечении от математической логики и был главный смысл ежедневных тренировок. Чтобы найти правильное решение, необходимо было представить себе «кусочек мира».
— Не сложновато для школьников?
— Если говорить об условных и безусловных рефлексах, младенец с рождения познает мир.
Если можно тренировать руки и ноги, то почему нельзя тренировать мозг?
— А не припомните ли какую-нибудь задачу той поры, казавшуюся неразрешимой?
— Неразрешимой… Пожалуй, нет. Труднорешаемой. Так точнее. Помните библейскую легенду о том, как Иисус Христос ходил по воде, аки посуху. Так вот мне нужно было рассчитать, с какой скоростью он должен был двигаться по водам, чтобы не провалиться.
— Вычисления оказались верными?
— Ну если легенда до сих пор существует, значит, и я не ошибся. Здесь нет никакой особой загадки. Благодаря нашим учителям мы уже достаточно хорошо изучили топологию – науку, позволяющую понять свойства пространства и оперировать формулами, понимая их прикладное значение, что помогает добиваться быстрых и точных результатов. Кстати, я тогда не считал победу на олимпиаде каким-то знаковым событием – это был всего лишь один из многих этапов познания в любимой науке.
Мог стать музыкантом
— А вы знаете, что мне пришлось поломать голову, выбирая профессию?
— Я имел право без экзаменов поступать в любое учебное заведение Советского Союза. Вот и колебался между мехматом и консерваторией. Выбрал математику… Мне сейчас очень интересно вспоминать студенческие годы. Мы так много успевали тогда… Процесс познания захватывал… Мы забывали о днях недели и времени года.
— В двадцать с небольшим лет вы сказали новое слово в науке…
— Никаких слов я не говорил… Просто продолжал исследовать проблемы изучения свойств трехмерного пространства Вселенной. Это очень интересно.
— Пытались объять необъятное?
— Совершенно верно… Только ведь любое необъятное тоже объятно. Диссертацию писал под руководством академика Александрова. Тема была несложной: «Седловидные поверхности в евклидовой геометрии». Можете представить себе в бесконечности равновеликие и неравномерно удаленные друг от друга поверхности? Нам нужно измерить «впадины» между ними.
— Это уже практика. По какой орбите полетит космический корабль к созвездию Псов? Какие препятствия встретит на своем пути… Хотите еще проще? Стоит ли косить сено между тремя холмами? Сколько людей и машин для этого надо? Министерство сельского хозяйства, оказывается, ни к чему. Есть формула. Пользуйся. Считай. И никакие кризисы тебе не страшны.
— А не схоластика ли это?
— Это колесо, топор, молот, наковальня – все что угодно, но только не схоластика. Давайте разберемся. Особенности современной математики заключаются в том, что она изучает искусственно изобретенные объекты. Нет в природе многомерных пространств, нет групп, полей и колец, свойства которых усиленно изучают математики. И если в технике постоянно создаются новые аппараты, всевозможные устройства, то и в математике создаются их аналоги – логические приемы для аналитиков в любой области науки. И всякая математическая теория, если она строгая, рано или поздно находит применение. К примеру, многие поколения математиков и философов пытались аксиоматизировать философию. В результате этих попыток была создана теория булевых функций, названных по имени ирландского математика и философа Джорджа Буля. Эта теория стала ядром кибернетики и общей теории управления, которые вместе с достижениями других наук привели к созданию компьютеров, современных морских, воздушных и космических кораблей. Таких примеров история математики
дает десятки.
— Значит, каждая ваша теоретическая разработка имеет прикладное значение?
— Безусловно. Для чего столько лет нужно было биться над доказательством гипотезы Пуанкаре? Попросту суть ее можно изложить так: если трехмерная поверхность в чем-то похожа на сферу, то ее можно расправить в сферу. «Формулой Вселенной» утверждение Пуанкаре называют из-за его важности в изучении сложных физических процессов в теории мироздания и из-за того, что оно дает ответ на вопрос о форме Вселенной. Сыграет это доказательство большую роль в развитии нанотехнологий.
— Значит, «бодрые» «жизнеутверждающие» доклады «пионеров» этой отрасли…
— Абсолютная чепуха и бессмыслица. Попытка построить дом на песке… Я научился вычислять пустоты, вместе с моими коллегами мы познаем механизмы заполнения социальных и экономических «пустот». Пустоты есть везде. Их можно вычислять, и это дает большие возможности… Я знаю, как управлять Вселенной. И скажите – зачем же мне бежать за миллионом?!
Новости Наука
28.04.2011
Новости , Кратко , Популярное
Архив
«Я знаю, как управлять Вселенной. Зачем мне миллион?!» Математик-затворник Григорий Перельман дал первое интервью
По информации «КП», проживающий в Израиле Александр Забровский вышел через еврейскую общину Петербурга сначала на мать Перельмана, которая рекомендовала сыну поговорить с журналистом. Забровский понравился математику и тот согласился на встречу. Более того, выдающийся ученый дал согласие на съемку художественную ленту «Формула Вселенной» с его участием. Это можно назвать достижением – журналистам ранее не удавалось «поймать» ученого, хотя они сутками караулили у его подъезда.
Григорий Перельман признался в беседе с Забровским, что не общается с российскими журналистами из-за неуважительного к нему отношения. Например, в прессе его называют «Гришей», рассказал ученый. Эта фамильярность его обижает.
Как рассказал Забровский, Перельман произвел впечатление «абсолютно вменяемого, здорового, адекватного и нормального человека»: «Реалистичный, прагматичный и здравомыслящий, но не лишенный сентиментальности и азарта… Все, что ему приписали в прессе, будто он «не в себе», – полная чушь! Он твердо знает, чего хочет, и знает, как добиться цели».
Фильм, ради которого математик пошел на контакт, будет не о нем самом, а о сотрудничестве и противоборстве трех основных мировых математических школ: российской, китайской и американской, наиболее продвинувшихся по стезе изучения и управления Вселенной.
По словам Григория Перельмана, он со школьной скамьи привык тренировать мозг, с тех пор для него не стало неразрешимых задач. При этом он признался, что мог стать не математиком, а музыкантом, и долго ломал голову над выбором профессии. «Я имел право без экзаменов поступать в любое учебное заведение Советского Союза. Вот и колебался между мехматом и консерваторией. Выбрал математику…», – рассказал ученый.
«Мне сейчас очень интересно вспоминать студенческие годы. Мы так много успевали тогда… Процесс познания захватывал… Мы забывали о днях недели и времени года», – признался математик.
Вспоминая, как получил золотую медаль на математической олимпиаде в Будапеште, он сказал: «Мы пытались решать задачи, где непременным условием было умение абстрактно мыслить. В этом отвлечении от математической логики и был главный смысл ежедневных тренировок. Чтобы найти правильное решение, необходимо было представить себе «кусочек мира».
В качестве примера такой «труднорешаемой» задачи он привел такую: «Помните библейскую легенду о том, как Иисус Христос ходил по воде, аки посуху. Так вот мне нужно было рассчитать, с какой скоростью он должен был двигаться по водам, чтобы не провалиться».
С тех пор всю свою деятельность Перельман посвятил исследованию проблемы изучения свойств трехмерного пространства Вселенной: «Это очень интересно. Я пытаюсь объять необъятное. Только ведь любое необъятное тоже объятно», – рассуждает он.
Диссертацию ученый писал под руководством академика Александрова. «Тема была несложной: «Седловидные поверхности в евклидовой геометрии». Можете представить себе в бесконечности равновеликие и неравномерно удаленные друг от друга поверхности? Нам нужно измерить «впадины» между ними», – пояснил математик.
В доказательстве теории Пуанкаре Перельман видит прикладное значение, так как она сыграет большую роль в развитии нанотехнологий: «Для чего столько лет нужно было биться над доказательством гипотезы Пуанкаре? Попросту суть её можно изложить так: если трехмерная поверхность в чем-то похожа на сферу, то ее можно расправить в сферу. «Формулой Вселенной» утверждение Пуанкаре называют из-за его важности в изучении сложных физических процессов в теории мироздания и из-за того, что оно дает ответ на вопрос о форме Вселенной. Сыграет это доказательство большую роль в развитии нанотехнологий».
Объяснил математик и причины отказа от награды: «Я научился вычислять пустоты, вместе с моими коллегами мы познаем механизмы заполнения социальных и экономических пустот. Пустоты есть везде. Их можно вычислять, и это дает большие возможности. Я знаю, как управлять Вселенной. И скажите, зачем же мне бежать за миллионом?!»
Григорий Перельман является объектом постоянного интереса спецслужб, не только российских, но и зарубежных, пишет «КП». Как объясняют в спецслужбах РФ, математик фактически шагает впереди сегодняшней мировой науки. Он постиг некие сверхзнания, помогающие понять мироздание. И тут возникают вопросы такого рода: «А что будет, если его знания найдут практическое воплощение?»
Как пишет издание, Перельман и сам понимает масштаб того, что он открыл. Он сам себя называет «человеком Вселенной». И, по слухам, опасается за свою безопасность – ведь его умная голова, уже оцененная в миллион долларов, стоит гораздо больше.
Математик Перельман окончательно отверг миллион долларов >>>
Москва, Ольга Панфилова
Москва. Другие новости 27.04.11
Дефицит абитуриентов породил серьезную конкуренцию среди уральских ВУЗов. О таких условиях поступления и учебы раньше можно было только мечтать. / Противники нового логотипа УрФУ перешли к активным действиям. Открытая встреча студентов и преподавателей пройдет в пятницу. / Школьные скандалы в Екатеринбурге дойдут до судов. Но системные проблемы это не решит. Читать дальше
После АБВГДейки мы читали Перельмана, а он говорил о науке с великими и объяснял её простым языком
138 лет назад 4 декабря в городе Белосток Гродненской губернии Российской империи родился будущий российский и советский учёный, один из основоположников жанра научно-популярной литературы и занимательной науки, автор понятия «научно-фантастическое», популяризатор точных наук, математик, физик, журналист и педагог Яков Исидорович Перельман.
Он не совершил никаких научных открытий, ничего не изобрёл в области техники, не имел никаких учёных званий и степеней. Однако до последней минуты жизни был предан науке и сумел передать и нам радость общения с ней.
Яков вырос в интеллигентной семье: его отец был счетоводом, а мать учительницей начальных классов. Глава семь рано умер, и Якова и его братьев и сестёр вырастила мама. Она смогла обеспечить детям возможность окончить Белостокское реальное училище, а позже и петербургский Лесной институт. В дипломе Якова значилось «учёный-лесовод I разряда».
Ещё во время учёбы в реальном училище Яков в возрасте 16 лет опубликовал свой первый труд. Это был очерк «По поводу ожидаемого огненного дождя» в газете «Гродненские губернские ведомости»: это был ответ некоему магистру, который взял на себя смелость «научно» предсказать миру скорый конец. В своём очерке Перельман легко и изящно развенчал мифы о метеоритных дождях и дал научное объяснение небесному феномену. Этот очерк вышел под псевдонимом «Я.П.», так как закон того времени запрещал учащимся публиковаться в прессе. Весь тираж был раскуплен мгновенно, а статью Перельмана ещё долго перечитывали и обсуждали.
В 1901 году, уже будучи студентом Лесного института, Яков Исидорович, начал сотрудничать с журналом «Природа и люди» (его первый очерк для издания назывался «Столетие астероидов»), а в 1905 году он стал ответственным секретарём в этом же журнале и проработал в нём без малого семнадцать лет. За это время на страницах журнала было опубликовано более пятисот его очерков, статей и заметок.
Многое из напечатанного затем вошло в первую часть книги Якова Перельмана «Занимательная физика», которая увидела свет в 1913 году, и имела грандиозный успех (вторая вышла через три года). Вызвала она интерес и в среде физиков. Профессор физики Петербургского университета Орест Данилович Хвольсон, познакомившись с Перельманом и узнав, что книга написана не учёным-физиком, а учёным-лесоводом, сказал Якову Исидоровичу: «Лесоводов-учёных у нас предостаточно, а вот людей, которые умели бы так писать о физике, как пишете Вы, нет вовсе. Мой вам настоятельнейший совет: продолжайте, обязательно продолжайте писать подобные книги и впредь». «Занимательная физика» была закуплена сразу несколькими петербургскими университетами.
В этом же году Перельман начал регулярную переписку с Константином Циолковским, которая продолжалась до последних дней жизни Циолковского. 20 ноября 1913 года Яков Перельман выступил с докладом в Российском обществе любителей мироведения «О возможности межпланетных сообщений», в основу которого легли идеи К. Э. Циолковского.
Кстати, к вопросу о единственном «изобретении» Перельмана. Вот любопытная история о создании им нового понятия. В 1914 году Яков Исидорович написал и опубликовал дополнительную главу «Завтрак в невесомой кухне» к роману Жюля Верна «Из пушки на Луну», которой дал определение «научно-фантастическая» (дело в том, что Жюль Верн свои романы называл научными, а Герберт Уэллс — фантастическими).
В 1915 году Яков Исидорович познакомился с врачом Анной Давидовной Каминской, и вскоре молодые люди поженились. Они сняли квартиру на Плуталовской улице, в доме №2, и с того дня Перельман указывал этот адрес во всех своих книгах.
В 1924 году участвовал в работе московской «Секции межпланетных сообщений» Осоавиахима СССР, в числе членов которой были Ф. Э. Дзержинский, К. Э. Циолковский, В. П. Ветчинкин, Ф. А. Цандер, Н. А. Рынин и другие.
В начале 1930-х годов Яков Исидорович заведовал отделом пропаганды в ленинградской группе изучения реактивного движения, разрабатывал проект первой отечественной противоградовой ракеты и при этом регулярно переписывался с Сергеем Павловичем Королёвым по вопросам пропаганды космических знаний.
В 1934 году Якову Перельману посчастливилось встретиться с популярным американским писателем-фантастом Гербертом Уэллсом во время его визита в Советский Союз.
За годы жизни Перельман издал более тысячи статей и заметок, не считая 40 научно-познавательных книг, 18 учебников. В СССР издавался более 450 раз, напечатано около 13 миллионов экземпляров его книг, наиболее известные из которых: «Живая математика», «Занимательная алгебра», «Занимательная арифметика», «Занимательная астрономия», «Занимательная механика», «Занимательная физика».
На счету у Перельмана немало и других весьма любопытных начинаний. Так, работая в 1916-1917 гг. в петроградском «Особом совещании по топливу», он впервые в России предложил перевести стрелку часов на час вперед в целях экономии горючего, что и было без промедления осуществлено.
Музей занимательных наук
В 1935 году учёный (думаю, у нас есть все основания именно так называть Якова Перельмана) создал в Ленинграде, в бывшем дворце графа Шереметьева, Дом занимательной науки и стал его научным руководителем. Это был один из самых удивительных музеев мира. Вместо хорошо известных надписей «Руками не трогать!» и «За ограждение не заходить!» здесь все экспонаты не только можно, но и нужно было трогать, крутить и даже пытаться сломать.
Торговые весы здесь отгадывали любое задуманное число или фамилию. В буфете из бутылки, которая стояла в кусочках колотого льда, наливали кипящий чай. А с виду металлическая чайная ложка таяла быстрее сахара, который она размешивала! (для любопытных: ложечка была отлита из сплава Вуда, плавящегося при температуре 68 градусов по Цельсию).
В музее можно было увидеть маятник Максвелла, двухметровую модель ракеты «по собственноручному эскизу Циолковского», доску Гальтона. Всего насчитывалось более пятисот удивительных экспонатов! Был даже зал Жюля Верна! И даже книга отзывов удивляла: едва посетитель садился за стол, она сама открывалась на нужной странице.
Естественно, что от экскурсий не было отбоя. Экспозиция музея постоянно росла, организаторы готовились открыть новые залы, но их планам не суждено было осуществиться — началась Великая Отечественная война. Музей пришлось закрыть в её первые дни, 29 июня. На фронт ушли многие сотрудники, в том числе директор В.А.Камский (он погиб на Волховском фронте), лекторы, художник. Многие экспозиции закопали в саду у Фонтанного дома, по некоторым сведениям, часть эвакуировали на Урал, но почти весь музей погиб в блокадном городе.
С началом Великой Отечественной войны Яков Исидорович остался в Ленинграде, где читал лекции об ориентировании на местности без приборов воинам-разведчикам нескольких фронтов и партизанам.
18 января 1942 года во время своего дежурства в госпитале умерла от истощения Анна Давидовна. Яков Исидорович Перельман пережил супругу всего на два месяца: он умер от голода в осаждённом Ленинграде 16 марта 1942 года. Умер, до последнего своего дня работая над тем, как помочь солдатам ориентироваться на местности, что должно было пригодиться им во время боевых действий.
Этот удивительный человек не считал себя учёным, а «лишь любителем поразмыслить».
Как здорово, что благодаря этим размышлениям появились замечательные книги и труды, благодаря которым уже несколько поколений легко увлекаются науками, а сложные знания становятся доступными в удивительном научно-фантастическом формате.
Про что эта серия АБВГДейки
В волшебном Двудесятом королевстве с математическим уклоном король Ноль проводит математический турнир, на который пригласил друзей из «АБВГДейки» вместе с её ведущей – Татьяной Кирилловной Черняевой. В математическом турнире решают примеры и задачи, а правильный ответ определяет победителя. Заметим, что задачи и примеры бывают не только на сложение и вычитание, но и на сообразительность.
АБВГДейка. Выпуск № 10. Математический турнир | Старые выпуски. 1985 г. Источник: канал на YouTube «Советское телевидение. Гостелерадиофонд СССР», www.youtube.com/c/gtrftv
В идеальном мире была бы премия за популяризацию науки им. Я.И.Перельмана
Пусть Перельман ничего глобального не изобрел не придумал, не открыл нового, но он сделал для популяризации науки настолько много, что заслуживает памяти в веках и памятника в граните.
На его Занимательной Физике, Математике, Геометрии, Астрономии выросло огромное количество великих ученых, многие мальчишки и девчонки прочитав его простые, понятные и безумно интересные книги пошли в науку и сделали множество открытий, с проектировали самолеты, пароходы, электростанции и всё благодаря действительно великолепным книгам «любителя поразмыслить»
Этот Человек с большой буквы очень сильно повлиял на мою жизнь. Я вырос на его книгах.
Была, была у меня такая книга. Читалась взапой, после чего учебная программа давалась легко и непринуждённо.
Когда читаешь его занимательную геометрию, находишь очень много про расстояния, высоты и прочее, что необходимо на местности.
Как ни странно, фамилия «Перельман» встречается довольно часто по отношению к наукам..
Распространено заблуждение, что Яков Исидорович Перельман является отцом известного математика Григория Яковлевича Перельмана[13]. Первый из них умер более, чем за 20 лет до рождения второго.
В послесловии А. Г. Мадеры к переизданию книги Я. И. Перельмана «Занимательные задачи» (М., 2001) Якову Исидоровичу Перельману приписано авторство статьи «Метод Б. Г. Галеркина в вариационном исчислении и в теории упругости» («Прикладная математика и механика», 1941). Однако автором этой статьи является другой Яков Перельман — тоже ленинградец, ученик академика Галеркина Яков Исаевич Перельман.
Спасибо за напоминание об этом увлеченном человеке.
Дополню статью большими подробностями:
1. Белосток. Детство и юность
Яков (Соломон-Яков) Исидорович Перельман родился 22 ноября (4 декабря) 1882 года в Белостоке — уездном городке Гродненской губернии. В 1897 году в городе насчитывалось шестьдесят шесть тысяч человек, в 1909 году — восемьдесят девять тысяч. Здесь были небольшие предприятия по обработке леса и кожи, стекольные и суконные фабрики.
Яков рано лишился отца: Исидор Перельман, германский подданный, счетовод суконной фабрики, скончался, когда младшему сыну было всего десять месяцев. Мать, Генриетта Исааковна, поднимала детей — трех сыновей и дочь Иоганну (Анну) — на жалованье учительницы младших классов и на заработки от частных уроков немецкого и французского языка. Потом стал работать старший сын Герман. Вместе с матерью он заботился об образовании детей: подбирал книги для чтения, выписывал столичные журналы. Под руководством старшего брата Яков делал первые физические опыты. Когда братья подросли, Герман уехал в Германию. Судьба его после 1933 года неизвестна.
Средний сын Иосиф, будущий русский писатель Осип Дымов, а затем и Яков, поступили в Белостокское реальное училище. Оно считалось лучшим во всей губернии. Действительно, здесь были прекрасные учебные кабинеты, библиотека насчитывала девять тысяч единиц хранения. С 1882 года действовало «Общество вспоможения нуждающимся воспитанникам», финансируемое частными лицами и отчасти городской управой. Самым бедным выдавали по три рубля на приобретение учебников.
Иосиф еще в училище начал писать. В 1892 году он опубликовал в журнале «Вокруг света» свой «Рассказ капитана». За это его чуть не исключили из училища: начальство все еще не оправилось от потрясения десятилетней давности, когда оказалось, что из Белостокского реального училища вышел один из народовольцев. Иосиф все-таки окончил училище и поступил в петербургский Лесной институт (будущая Лесотехническая академия).
Яков продолжал учиться. Ему легко давались математика и — особенно — физика. Математик А. А. Мазулов часто проводил занятия по геометрии на вольном воздухе (отсюда и название одной из частей «Занимательной геометрии» — «Геометрия на вольном воздухе»), предлагал внепрограммные задачи, подбирал для учеников литературу по истории математики, а главное — учил мыслить нестандартно. Физику преподавал Е. А. Бунимович, окончивший Петербургский Университет. Он умел учить увлекательно и занимательно. Латынь и греческий язык в реальных училищах не преподавались, так что для изучения естественных наук оставалось больше времени.
Как раз тогда Яков прочитал «Уранию» Фламмариона и увлекся астрономией. В начале 1899 года поползли слухи о близком конце света: на Землю-де выпадет огненный дождь. Реалист Перельман понимал, что этот «дождь» — не что иное, как поток метеоритов, наблюдаемый три раза в столетие, когда Земля проходит близ созвездия Льва. Земле он не приносит никакого вреда.
23 сентября (5 октября) 1899 года «Гродненские губернские ведомости» напечатали статью за подписью Я. П. «По поводу ожидаемого огненного дождя». За эту статью Яков получил семь рублей двенадцать копеек.
В 1901 году Яков Перельман окончил реальное училище. Он подал документы в Лесной институт, где уже учился его брат. Принимали по конкурсу аттестатов. В аттестате Перельмана не было отметки по закону божьему. Брат Иосиф через директора императорских театров И. А. Всеволожского обратился к министру земледелия, и 25 октября (7 ноября) 1901 года Яков был зачислен.
Есть у меня «Занимательная физика» издания 1947 года. Много раз перечитывалась и мной, и сыном. И «Занимательная математика» тоже где-то лежит среди книг.
Может, с Циолковским переписывался, а не с Королёвым? Королёв в начале 30-ых был слишком молод.
Почему гелий меняет наш голос, а также что такое инертные газы
На уроках химии мы слышали об инертных газах. Их еще называют благородными, такое красивое название было дано не с проста, ведь все инертные газы, а именно гелий, неон, аргон, криптон, ксенон, а также радиоактивные радон и оганесон обладают очень низкой химической активностью, их соединения с другими веществами существуют лишь в специальных, экстремальных условиях, а значит, эти газы не горят и не поддерживают горение, более того, не имея цвета, запаха и вкуса они не токсичны для человека, их вообще как будто нет, настоящее благородство!)
Но это не совсем так, инертные газы хоть и не отравляют человека, но наркотически действуют на него, однако это не относится к гелию и неону, поскольку их наркотический эффект проявляется при очень повышенном давлении, впрочем, поэтому наркоманы и не дышат шариками с гелием.
Интересным фактом является то, что инертные газы переходят в жидкое состояние при экстремально низких температурах, при этом почти сразу после переходя в твердое состояние. Таким образом разница между температурой кипения и плавления у веществ состовляющих инертные газы 2-5, максимум 10 градусов.
Вообще гелий удивителен. Во Вселенной он второй по распространенности после водорода, но на Земле существует в совсем малых количествах, однако не беспокойтесь, на надувание шариков всем хватит). Из за практически самого малого размера атомов гелия, они почти не сталкиваются друг с другом, когда гелий находится в газообразном состоянии, что делает гелий идеальным газом (идеальный газ это такая теоретическая модель, можете посмотреть о ней в Википедии подробнее).
Еще одна занимательная вещь, что гелий, как и все инертные газы светится при пропускании через него электрического тока. Причем при изменении давления внутри газа, можно менять его цвет. Это связанно с тем, что с увеличением давления, электроны начинают чаще сталкиваться с атомами гелия и общая энергия вещества увеличивается, приводя к изменению цвета. Так гелий может светиться желтым, розовым, оранжевым и зеленым цветами.
Но мы то все знает гелий как веселый газ, смешно изменяющий наш голос. Почему так происходит? Тут нужно разобраться, что вообще такое звук, издаваемый нами при выдохе.
По простому звук есть колебание молекул или других мельчайших частиц среды, улавливаемое нашим ухом. Такой средой является воздух. Когда мы издаем какие либо звуки, наши голосовые связки вибрируют, создавая колебания среды, то есть воздуха. Чем чаще колеблятся связки, тем выше высота звука. Если мы вдохнем вместо воздуха гелий, он станет средой для распространения звука. Но из за гораздо меньшей плотности гелия, он создает меньшее давление на голосовые связки, чем воздух, позволяя им вибрировать быстрее и издавать более тонкий звук.
Так, для понижения голоса можно вдохнуть плотный газ, например фторид серы, он в 5 раз тяжелее воздуха и сильно понижает частоту колебаний голосовых связок, позволяя Вам говорить как Халк:).
Дорога жизни
А давайте вспомним историю. 80 лет назад в ходе Великой Отечественной войны была открыта «Дорога жизни».
Дорога жизни – единственная военно-стратегическая транспортная магистраль, связывавшая во время Великой Отечественной войны (1941-1945) с сентября 1941 года по март 1943 года осажденный германскими войсками Ленинград (ныне Санкт-Петербург) с тылом страны. Проходила через Ладожское озеро.
Историю нужно знать и помнить, без этого конечно никак.
Ну логично же ответил
Олимпиада по математике 3 класс
Ответ на пост «Забавная арифметика»
Что-то очень похожее я видел в книге Ричарда Фейнмана «Вы, конечно, шутите, мистер Фейнман!», в той главе, где он рассказывал о своём участии в оценке новых учебников по математике.
Квантовая теория поля: визуализация от ScienceClic
Как согласовать теорию относительности с квантовой механикой? Что такое спин? Откуда берётся электрический заряд?
Инопланетянин
Это маленький, миленький, забавный инопланетянин. Чаще всего нам привычно представлять «гостей из космоса» именно в таком образе. Так почему бы и не создать именно такого кроху.
Связан из ниточек Пехорка «Цветное кружево» и крючком 0.7 мм. Внутри каркас из медной проволоки. Маленькие стразы на теле и голове.
Не смогла остановится и создала ещё одного «гостя», только в зелёном цвете
Друг в беде не бросит, лишнего не спросит.
25 часов в сутки
Что такое наука и какие задачи она должна решать? Существует ли музыкальная наука и какими могут быть результаты применения научного метода в этой сфере? Что такое микрохроматика и как она может изменить музыку будущего, расширить возможности её создания и восприятия?
Просьба улучшить качество фильма о теории относительности
В 1964 году Моснаучфильмом был снят замечательный образовательный фильм о теории относительности. Причём с известнейшими актёрами той эпохи: Георгий Вицин, Алла Демидова, Алексей Полевой. Сейчас такого уже никто не снимет.
Хочу показать этот фильм своим ученикам на вводном занятии по теории относительности, но качество оставляет желать лучшего. Самый качественный вариант я нашёл в VK: https://vk.com/video314558845_456239179, но там всего 480p.
Уважаемые @Mrsatana666666, @shivam, @Inquabator и все, кто занимается повышением качество видео, не могли бы вы улучшить эту короткометражку? Заранее спасибо.
История проблемы равенства классов P и NP
В 2000 году Математический институт Клэя определил 7 математических задач, решение которых не могли найти в течение многих лет. За решение каждой из них была назначена награда в размере 1 миллиона долларов. Эти 7 задач известны как «задачи тысячелетия», и на сегодняшний день только одна из них была решена — гипотеза Пуанкаре. В этой статье пойдет речь о вопросе равенства классов P и NP, ответ на который может сильно повлиять на всю IT-сферу.
Равенство P и NP классов отсылает нас к теории алгоритмов, а именно к классам сложности. Первое, с чего стоит начать, это то, что классы P и NP классифицируют языки, а не задачи. Пока что это звучит довольно абсурдно, поэтому для понимания разберемся в некоторых деталях.
Пусть А — алфавит и L ⊆ А*, тогда L называется языком над А. Для любого алфавита пустое множество и А* являются тривиальными языками. При этом пустое множество часто называют пустым языком. Однако не стоит путать пустой язык и язык, содержащий пустое слово e, — они различны. Языки могут быть как бесконечными, так и нет, но обязательно счетными. Т. е. множество всех действительных чисел языком нельзя назвать, т. к. такой набор является неисчисляемым.
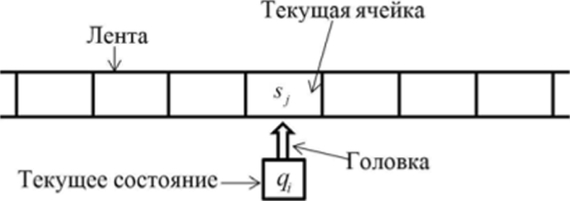
Говоря про абстрактный исполнитель, чаще всего имеют в виду машину Тьюринга, поэтому в дальнейшем под АИ будем подразумевать именно её. Итак, машина Тьюринга имеет неограниченное линейное хранилище, сгруппированное в ячейки. Каждая ячейка может содержать ровно один символ алфавита в любой момент времени. Вдоль ячеек идет считывающая головка, имеющая конечное число состояний. За одну итерацию она может считать значение только одной ячейки, переписать её значение, изменить свое состояние и перейти на одну позицию вправо/влево.
Устройство машины Тьюринга
На основе машины Тьюринга определим так называемую разрешающую машину над языком. Для начала введем определение характеризующей функции X(w). Функция X определяет, принадлежит ли слово w языку L. Если да, то значение функции равно «1»; если нет, то «0». Формально это можно записать так:
Разрешающей машиной D для языка L называется такая машина, которая для каждого w∈A вычисляет характеризующую функцию X(w) за конечное время.
В дополнение к разрешающей машине идет верификатор. Машина V, которая принимает слова w и c и выводит 0 или 1 после конечного числа шагов, называется верификатором для L, если она обладает следующими свойствами:
— выводит 1, только если w входит в язык L;
— для любого w в языке L существует такое c, что V(w,c) = 1.
Классы сложности и формулировка проблемы
Окей, мы рассмотрели несколько понятий. На первый взгляд, все это больше походит на лингвистику: алфавиты, слова, языки… Причем тут задачи? Чтобы ответить на этот вопрос, обратимся к понятию задача разрешимости (англ. Decision problem). Это такой вопрос (сформулированный в формальной системе), требующий ответа «да» или «нет», зависящего, возможно, от значений некоторых входных параметров. Например, «является ли данное натуральное число x простым?» или «даны два числа: x и y; делится ли x на y?« Метод решения в виде алгоритма называется разрешающей процедурой. Теория вычислимости имеет дело в основном с задачами разрешимости и приведенные выше конструкции наглядно соотносятся с таким типом задач: так разрешающая машина над языком является формализацией разрешающей процедуры. Но как же быть с задачами, такими как задача коммивояжера? На них нельзя дать бинарный ответ. В таких случаях применяют приемы приведения к версии decision problem. В случае коммивояжера проблема по-новому формулируется так: «существует ли маршрут не длиннее, чем заданное значение k?»
В класс сложности NP входят все языки L, для которых существует такой верификатор, что для каждого (w,c) время его работы полиномиально. Иными словами, NP включает в себя задачи разрешимости, для которых при подходящем сертификате для данного w мы быстро сможем удостовериться в том, что w действительно принадлежит L (ответ на вопрос можно довольно быстро проверить). Отсюда и название «верификатор». В качестве примера задачи в NP можно привести определение наличия в графе гамильтонова цикла. Сертификат в данном случае — последовательность вершин, образующих гамильтонов цикл.
Помимо этих классов можно выделить ещё 2: NP-hard и NP-Complete. Они основываются на приводимости одного языка к другому за полиномиальное время: пусть языки A и B — языки над одним алфавитом. Язык А будет приводимым за полиномиальное время к языку B, если существует такая функция f(w), что
— функция f может быть вычислена машиной Тьюринга за полиномиальное время.
Тогда в класс NP-hard будут входить языки, к которым приводимы все языки в NP (причем NP-hard язык может входить в NP, а может и нет), а в NP-Complete те языки, которые являются одновременно NP-hard и NP. Примером NP-Complete является язык выполнимых булевых формул (SAT). Таким образом, NP-Complete задачи образуют в некотором смысле подмножество «типовых» задач в классе NP: если для какой-то из них найден «полиномиально быстрый» алгоритм решения, то и любая другая задача из класса NP может быть решена так же «быстро».
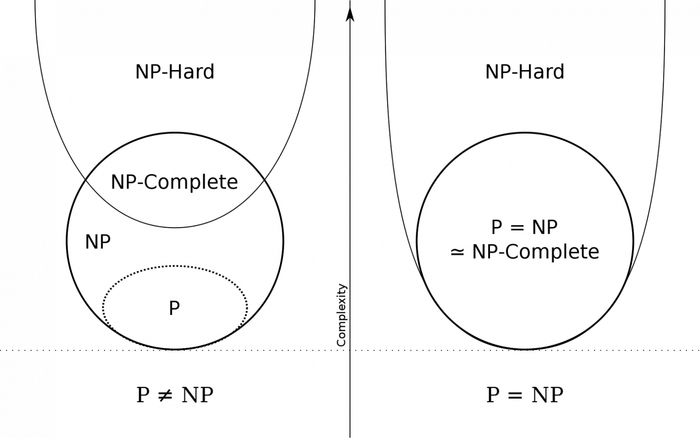
Отношение между классами при равенстве и неравенстве
Теперь, немного погрузившись в теорию алгоритмов, более конкретно обозначим проблему равенства данных классов. Итак, множество P входит в множество NP, но неизвестно, существуют ли языки, которые входят в NP и не входят в P. Что это означает на практике? Итак, простыми словами класс NP можно охарактеризовать как «трудно решить, легко проверить». Классическим примером задачи, входящей в NP, является задача коммивояжера, для решения которой на данный момент известен лишь один алгоритм — старый добрый перебор (мы не рассматриваем эвристические методы). Однако, получив ответ, его будет не так сложно проверить. Класс P же вобрал в себя те задачи, для которых существует эффективный алгоритм решения, позволяющий решать их за полиномиальное время. И равенство или, наоборот, неравенство этих классов пока не доказано. Если эти классы равны, то это будет значить, что для всех задач, которые сейчас решаются путем перебора или другим неэффективным методом, существует(-ют) полиномиальные алгоритмы. А если не равны, то придется смириться с неоптимальностью решения этих задач.
История проблемы равенства P и NP началась в 1928 году, когда Давид Гильберт сформулировал проблему, названную Entscheidungsproblem (нем. задача разрешения). Ее суть заключается в нахождении алгоритма, определяющего доказуемость данного утверждения из аксиом с использованием правил логики. По названию очевидно, что это задача является задачей разрешения (выводит «да» или «нет»).
В ходе решения этой проблемы потребовалось определить термины «алгоритм» и «вычислимая функция». В 1936 году Алонзо Чёрч и Алан Тьюринг независимо показали, что общее решение Entscheidungsproblem невозможно, предположив, что интуитивное понятие «эффективная вычислимость» соответствует вычислимости функции на машине Тьюринга. Эта гипотеза сегодня известна как тезис Чёрча-Тьюринга.
20 марта 1956 в письме к Джону фон Нейману Курт Гёдель впервые поставил вопрос о вычислительной сложности. Гёдель интересовался, можно ли получить доказательство теоремы (в математико-логическом смысле слова) за квадратичное или линейное время. К сожалению, письмо было обнаружено лишь в 1989 году и получило широкую огласку, когда Юрис Хартманис опубликовал перевод и комментарий.
Статья Алана Кобэма 1965 года под названием «The intrinsic computational difficulty of functions» является одним из первых упоминаний класса сложности P, состоящего из разрешимых за полиномиальное время задач. Тезис Кобэма-Эдмондса (известный также как расширенный тезис Чёрча-Тьюринга), названный в честь Алана Кобэма и Джека Эдмондса, утверждает, что любая разумная модель вычислений может быть выражена через другую модель с замедлением, не более чем полиномиальным по размеру входных данных. Кобэм предположил, что класс P может быть хорошим способом для описания множества реально вычислимых задач. Любая проблема, не содержащаяся в P, невозможна, но если задача реального мира может быть решена с помощью алгоритма, существующего в P, то такой алгоритм в конечном итоге будет открыт.
В 1965 году Юрис Хартманис и Ричард Стернс опубликовали статью «On the Computational Complexity of Algorithms», отмеченную премией Тьюринга. В ней даются более точные определения сложности алгоритма и класса сложности. Хартманис и Стернс определили класс сложности как совокупность всех задач, которые можно решить за установленные временные рамки. В их статье показано, что существует бесконечная иерархия классов сложности (например, задачи, для которых наиболее быстрый алгоритм имеет время, пропорциональное n, n log n, n^2, n^3, 2^n и т. д.), где небольшое увеличение временного интервала позволяет решать больше задач. Во второй статье Хартманис совместно с Филипом М. Льюисом показали, что подобная иерархия существует и для количества памяти (функция от размера входа) при решении задачи на машине Тьюринга.
В 1967 году Мануэль Блюм разработал аксиоматическую теорию сложности, которая основана на его собственных аксиомах (аксиомы Блюма), и получил важный результат — теорему об ускорении. До этого мы говорили по большей части о сложности алгоритма. Хотелось бы аналогичным образом определить и сложность задачи: например, какова сложность самого эффективного (по времени и емкости) алгоритма, решающего эту задачу. Теорема об ускорении гласит, что есть некоторые задачи, для которых не существует самого быстрого алгоритма, потому что любой алгоритм для такой задачи можно «ускорить», построив более быстрый алгоритм.
Точная формулировка проблемы равенства P и NP была представлена в 1971 году. Тогда американский ученый Стивен Кук и работавший независимо советский ученый Леонид Левин доказали, что существуют практически актуальные проблемы, которые являются NP-полными. В США Стивен Кук опубликовал статью «The complexity of theorem proving procedures», в которой формализовал понятия редукции за полиномиальное время и NP-полноты, а также доказал существование NP-полной задачи (задача выполнимости булевых формул, SAT). Теорема была независимо доказана Леонидом Левиным и, таким образом, получила название «теорема Кука-Левина».
В 1972 году Ричард Карп сделал рывок в знаменитой статье «Reducibility among Combinatorial Problems», в которой показал, что около 20 разнообразных задач из комбинаторики и теории графов, известных своей вычислительной трудностью, являются NP-полными.
В августе 2010 года Виней Деолаликар, работавший в исследовательском отделении Hewlett-Packard в Пало-Альто в Калифорнии, заявил, что разгадал загадку P vs NP. Он утверждал, что P не равняется NP, однако научное сообщество нашло в его доказательстве фатальную ошибку. В начале 2002 года SIGACT News провел опрос среди 100 ученых, задав им вопрос о равенстве классов NP и P. 61 человек ответили, что «неравны», 9 — «равны», 22 затруднились ответить и 8 сказали, что гипотеза не выводима из текущей системы аксиом и, таким образом, не может быть доказана или опровергнута.
К чему приведет решение проблемы
Окей, теория вычислимости, формализация алгоритмов и абстрактные математические теории — все это конечно интересно, но как решение проблемы равенства NP и P классов отразится на практике? На самом деле, алгоритмы для решения NP-задач используются каждый день во многих сферах. Например, в криптографии, криптовалютах, восстановлении поврежденных файлов, системах блокировки спама, оптимизации в логистике и т. д. Более эффективные решения могли бы значительно сэкономить время и деньги, так как мы пользуемся в основном эвристическими методами, дающими лишь приближенные решения.
Однако существует и обратная сторона монеты. Солидная часть криптографии (криптосистемы с открытым ключом, технологии доказательства выполнения работы в блокчейне, системы блокировки спама) основывается на предположении о неравенстве NP и P классов. Если окажется, что некоторые задачи, для которых, как считалось, не существует эффективных алгоритмов, можно решать быстро, то многие методы защиты устареют.
Может оказаться и так, что последствия решения окажутся не такими тривиальными, как это часто и бывает в математике. В качестве примера рассмотрим континуум-гипотезу о существовании мощности, меньшей континуума и большей мощности счетного множества. Оказывается, существование такого кардинала нельзя ни доказать, ни опровергнуть в аксиоматике ZFC. Так что мы вправе считать, что такие мощности бывают (впрочем, как и считать, что не бывают). Однако ясно, что мы не можем конструктивно построить соответствующее множество. Возможно, точно также окажется и с алгоритмами для NP-задач в случае равенства NP и P (к слову, некоторые математики в опросе SIGACT News так и ответили: гипотеза не выводима из существующей системы аксиом, то есть не может быть доказана или опровергнута).
Пока что существующих методов доказательств недостаточно для строго математического ответа, но не нужно терять надежду. В марте 2001 года Ричард Карп предсказал, что проблема будет решена молодым математиком (до 30 лет) с использованием подхода, о котором еще никто не думал. Стивен Кук заявил, что кто-нибудь предоставит убедительное доказательство в ближайшие 20 лет.
Про радугу
Совсем немного о природе радуги
Рубрика «Ядерная физика от А до Я».
Научные сотрудники и преподаватели МИФИ объясняют термины из ядерной физики, физики элементарных частиц, астрофизики и космологии простыми словами.
Как мою бабушку в плен угоняли
Под случайно оставленным комментарием прилетело две просьбы написать пост об этой истории. Напишу, что знаю и что помню. Тема – дети во времена ВОВ (к вопросу о том, могут ли люди, к примеру, 1939 или 1941 годов рождения считаться прошедшими войну).
Моя бабушка Надежда родилась в 1936 году. Жила со своей матерью Фёклой (моей прабабушкой, соответственно), отцом Денисом, сестрой и братом где-то в деревне Калужской области. Прадед ушел на фронт, а Фёклу с детьми взяли в плен и угнали в Германию. После путешествия на поезде, в жуткой давке, без еды и воды, их поместили в концентрационный лагерь.
Спустя время некоторых достаточно здоровых детей из концлагеря стали продавать немцам в качестве слуг. Такая участь постигла двух из детей Фёклы – Надю, которой было 7 лет, и Колю, который был на пару лет постарше.
Семья, в которой оказалась маленькая Надя, купила ее в качестве рабочей силы себе и игрушки своему ребенку. Девочке приходилось таскать воду, дрова, помогать на кухне. Иногда ее запрягали в небольшую повозку, как лошадь, и она катала сына своих хозяев, а тот погонял ее кнутом. Надю мало кормили, много били. Но она осталась жива, тогда как в концлагере огромное количество детей тем временем просто умирало от голода.
Судьба ее брата, Николая, сложилась более удачно. Его взяла себе супружеская пара, у которой не было своих детей, и приемные родители стали относиться к 9-летнему Коле как к родному сыну. Когда в 1945 году освобожденная Фекла собирала свою семью, чтобы вернуться в Россию, эта немецкая пара очень просила оставить им мальчика, которого они полюбили, но Фекла не согласилась оставить сына в чужой стране. (А так был бы у меня сейчас двоюродный дед в Германии, или как там правильно брат бабушки называется).
Третий ребенок Фёклы, Антонина, была совсем еще малышкой, ей не было и годика. Ее оставили с матерью в концлагере. Сохранить грудного ребенка стоило ее матери больших трудов. Прабабушку к тому времени определили работать на военный завод вместе с десятками других пленных. Фекла была невысокая, хрупкая, худенькая, но очень волевая женщина. После войны она рассказывала, что в лагере открыто ругала последними словами и Гитлера, и Сталина, допустивших эту войну. Одному эсэсовцу, сотруднику лагеря, очень понравилось, как маленькая русская женщина трехэтажным матом ругает правителя своей страны. Он иногда за это подкармливал ее и маленькую Тоню, закрывая глаза на то, что вместе со Сталиным изрядно достается и Гитлеру. Кстати, на каком языке беседовали, понятия не имею. Маловероятно, что крестьянская женщина знала немецкий матерный. Или там понахваталась. Это, в общем, со слов прабабушки, как она рассказывала моей матери.
Когда наши войска в 1945 году освободили пленных на территории Германии, Фёкла собрала всех своих детей и вернулась на родину. Все дети остались живы, что было неслыханной удачей для того времени. Мой прадед с войны не вернулся. О нем не было вестей с самого начала войны. Уже намного позже внуки наши в архивах информацию, что вскоре после начала войны Денис Ефимович попал в плен под Вязьмой, был помещен в концлагерь в Бремене и через месяц там скончался.
Бабушка Надя умерла в 1989, когда мне было всего 6 лет. История записана по рассказам мамы в основном. Я в дошкольном возрасте этими вещами не особо интересовалась. Для меня в бабушке Наде было самым офигенным то, что она вышила ковер. Крестиком. Большой ковер. И повесила его на стену. Там было какое-то здание, цветы. Я смотрела на бабушку и пыталась представить, сколько времени она этот ковер вышивала. По моим прикидкам, начала еще в детстве, а закончила незадолго до моего рождения. Уже при мне бабушка… начала второй ковер! Красивый, с цветами. Так и не закончила, к сожалению. Но вышивать и вязать меня научила.
Сейчас жутко представить, через что пришлось пройти и детям, и взрослым во время ВОВ. Да и после войны жизнь была не сахар. После возвращения из плена моя прабабушка поняла, что она, одинокая женщина, не сможет в такой голод сохранить в живых всех троих детей. В то время как раз русские освободили от японцев остров Сахалин, и она с детьми поехала туда по программе переселения. На Дальнем Востоке еды было больше, последствий войны меньше, и Фекла одна, без мужа, подняла на ноги всех троих детей.
Со стороны отца никто никого никуда не угонял. Была моя прабабушка Анна с дочерью. Жили они в Ивановской области, и во времена ВОВ обе работали на ткацкой фабрике. Бабушке лет 14 было тогда. Прабабушку помню еще живой. К концу жизни она потеряла зрение (полностью) и слух (почти полностью), но в остальном, вроде, была вполне адекватной. Врачи говорят, оглохла, потому что всю жизнь трудилась в постоянном шуме станков. Когда меня в дошкольном возрасте привозили в гости, бабушка ставила меня перед своей мамой, кричала ей со всей силы в ухо, что вот, правнучка приехала. Прабабушка ощупывала мое лицо, волосы. А я ее побаивалась, хоть и понимала, что это не ведьма из сказки, а бабушкина мама. Вот бабушка – это да, она добрая, печет офигенные пирожки, у нее длинная седая коса под платком (всегда мечтала о длинных волосах, но мама меня стригла под каре), куча интересных историй и всегда есть конфетка в заначке… Жаль, что я больше любила слушать сказки, а не реальные истории из жизни того поколения. Когда подросла и стала понимать значимость исторической информации, хотела расспросить, но всё «потом», «в следующий раз»… Не успела, короче.
 drumsmen
drumsmen