что значит аппроксимировать функцию

Вычислительная математика копия 1

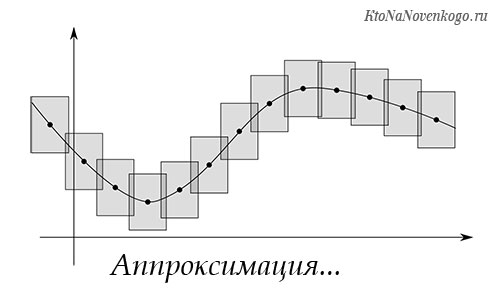
Аппроксимация – замена одной функции f(x) другой, похожей функцией Q(x). Например, функцию, полученную экспериментально в виде таблицы или графика, надо записать в аналитическом виде, либо функцию, достаточно сложную нужно заменить похожей, но более простой.

Простейший способ аппроксимации – замена функции f(x) алгебраическим полиномом

Необходимо так подобрать коэффициенты в формуле (2.1), чтобы Q(x, c_j ) как можно меньше отличалась от f ( x ).

2.1 Меры погрешности аппроксимации

1. Равномерное приближение

a) точечная аппроксимация

Подберем коэффициенты с_j таким образом, чтобы R было минимальным:

Это есть минимаксный подход, который осуществляет равномерное приближение функций.

b) интегральная аппроксимация

Критерий (2.3) перепишется в виде:

2. Метод наименьших модулей

a) точечная аппроксимация

b) интегральная аппроксимация

3. Метод наименьших квадратов

Чаще всего при точечной аппроксимации используют меру

а коэффициенты с j ищут из условия

Это точечная квадратичная аппроксимация.

При интегральной аппроксимации

Описанный подход к задаче аппроксимации называется методом наименьших квадратов. Условия (2.9) и (2.10) геометрически означают: из всех кривых заданного вида выбирают ту, у которой сумма площадей квадратов отклонений – наименьшая.

2.2 Нахождение коэффициентов c_j при точечной аппроксимации методом наименьших квадратов

Пример: построить аппроксимирующую параболу для функции

Источник

Электронная библиотека

Аппроксимацией (приближением) функции называется нахождение такой функции (аппроксимирующей функции), которая была бы близка заданной. Критерии близости функций и могут быть различные.

Основная задача аппроксимации — построение приближенной (аппроксимирующей) функции, в целом наиболее близко проходящей около данных точек или около данной непрерывной функции. Такая задача возникает при наличии погрешности в исходных данных (в этом случае нецелесообразно проводить функцию точно через все точки, как в интерполяций) или при желании получить упрощенное математическое описание сложной или неизвестной зависимости.

Рис. 3.6 Метод Лагранжа

Близость исходной и аппроксимирующей функций определяется числовой мерой

— критерием аппроксимации (близости). Наибольшее распространение получил квадратичный критерий, равный сумме квадратов отклонений расчетных значений от «экспериментальных» (т.е. заданных), — критерий близости в заданных точках:

Здесь у_i — заданные табличные значения функции; у_i расч — расчетные значения по аппроксимирующей функции; b_i — весовые коэффициенты, учитывающие относительную важность i-и точки (увеличение b,. приводит при стремлении уменьшить R к уменьшению, прежде всего отклонения в i—й точке, так как это отклонение искусственно увеличено за счет относительно большого значения весового коэффициента).

Квадратичный критерий обладает рядом «хороших» свойств, таких, как дифференцируемость, обеспечение единственного решения задачи аппроксимации при полиномиальных аппроксимирующих функциях.

Другим распространенным критерием близости является следующий:

Этот критерий менее распространен в связи с аналитическими и вычислительными трудностями, связанными с отсутствием гладкости функции и ее дифференцируемости.

Выделяют две основные задачи:

1) получение аппроксимирующей функции, описывающей имеющиеся данные, с погрешностью не хуже заданной;

2) получение аппроксимирующей функции заданной структуры с наилучшей возможной погрешностью.

Чаще всего первая задача сводится ко второй перебором различных аппроксимирующих функций и последующим выбором наилучшей.

Метод наименьших квадратов

Метод базируется на применении в качестве критерия близости суммы квадратов отклонений заданных и расчетных значений. При заданной структуре аппроксимирующей функции у_i расч (х) необходимо таким образом подобрать параметры этой функции, чтобы получить наименьшее значение критерия близости, т.е. наилучшую аппроксимацию. Рассмотрим путь нахождения этих параметров на примере полиномиальной функции одной переменной:

Запишем выражение критерия аппроксимации при b_i =1 (i=1, 2,…, n) для полиномиального у_i расч (х):

Искомые переменные а_j можно найти из необходимого условия минимума R по этим переменным, т.е. dR / dа_р = 0 (для _р =0, 1,2,…,k). Продифференцируем по а_р (р — текущий индекс):

После очевидных преобразований (сокращение на два, раскрытие скобок, изменение порядка суммирования) получим

Перепишем последние равенства

Получилась система n+1 уравнений с таким же количеством неизвестных а_j, причем линейная относительно этих переменных. Эта система называется системой нормальных уравнений. Из ее решения находятся параметры а_j аппроксимирующей функции, обеспечивающие minR, т.е. наилучшее возможное квадратичное приближение. Зная коэффициенты, можно (если нужно) вычислить и величину R (например, для сравнения различных аппроксимирующих функций). Следует помнить, что при изменении даже одного значения исходных данных (или пары значений х_i, у_i, или одного из них) все коэффициенты изменят в общем случае свои значения, так как они полностью определяются исходными данными. Поэтому при повторении аппроксимации с несколько изменившимися данными (например, вследствие погрешностей измерения, помех, влияния неучтенных факторов и т.п.) получится другая аппроксимирующая функция, отличающаяся коэффициентами. Обратим внимание на то, что коэффициенты а_j полинома находятся из решения системы уравнений, т.е. они связаны между собой. Это приводит к тому, что если какой-то коэффициент вследствие его малости захочется отбросить, придется пересчитывать заново оставшиеся. Можно рассчитать количественные оценки тесноты связи коэффициентов. Существует специальная теория планирования экспериментов, которая

позволяет обосновать и рассчитать значения х_i, используемые для аппроксимации, чтобы получить заданные свойства коэффициентов (несвязанность, минимальная дисперсия коэффициентов и т.д.) или аппроксимирующей функции (равная точность описания реальной зависимости в различных направлениях, минимальная дисперсия предсказания значения функции и т.д.).

Рис. 3.7 Влияние степени аппроксимирующего полинома М на точность аппроксимации

В случае постановки другой задачи — найти аппроксимирующую функцию, обеспечивающую погрешность не хуже заданной, — необходимо подбирать и структуру этой функции. Эта задача значительно сложнее предыдущей (найти параметры аппроксимирующей функции заданной структуры, обеспечивающей наилучшую возможную погрешность) и решается в основном путем перебора различных функций и сравнения получающихся мер близости. Для примера на рис. 3.7 приведены для визуального сравнения исходная и аппроксимирующие функции с различной степенью полинома, т.е. функции с различной структурой. Не следует забывать, что с повышением точности аппроксимации растет и сложность функции (при полиномиальных аппроксимирующих функциях), что делает ее менее удобной при использовании.

Рассмотрим решение задачи аппроксимации и интерполяции с шумом в

программе MathCAD (рисунок 3.8).

Источник

Аппроксимация

Добавлено в закладки: 0

Что такое аппроксимация – это научный метод, который можно использовать в разных областях познания. В дословном переводе он означает «приближение», и под ним подразумевается замена одних объектов, которые изучаются, на другие, схожие с исходными и более простые.

Метод аппроксимации дает возможность проводить исследования разных характеристик объектов, например, их качественных и числовых свойств.

Это достигается тем, что эти свойства сводятся к характеристикам объектов, которые уже известны, или гораздо легче определяются.

Рассмотрим, более детально, ч то значит аппроксимация. Аппроксима́ция, или приближе́ние являются научным методом, состоящим в замене одних объектов другими, в каком-то смысле близкими к исходным, однако более простыми.

Аппроксимация дает возможность исследовать качественные свойства и количественные характеристики объекта, сводя задачу к изучению более удобных или более простых объектов (к примеру, таких, свойства которых легко вычисляются или свойства которых известны уже). В теории чисел изучают диофантовы приближения, в частности, приближения рациональными иррациональных чисел. В геометрии рассматривают аппроксимации кривых ломаными. Определенные разделы математики целиком посвящены в сущности аппроксимации, к примеру, теория приближения функций, количественные методы анализа.

В переносном смысле употребляют в философии как способ приближения, указание на неокончательный, приблизительный характер. К примеру, в таком смысле термин «аппроксимация» употреблялся активно Сёреном Кьеркегором (1813—1855) в «Заключительном ненаучном послесловии…»

Остаточный член

Остаточный член — разница меж аппроксимирующей функцией и заданной функцией. Оценка остаточного члена тем самым является оценкой точности рассматриваемой аппроксимации. Данный термин используется, к примеру, в формуле ряда Тейлора.

Примеры

Когда функция будет применяться лишь для интерполяции, то достаточно аппроксимировать точки полиномом, скажем, пятой степени:

Гораздо сложней обстоит дело, когда изменения с граничными условиями. Тут уже качество итога зависит от профессионализма исследователя.

Для оптимального выбора параметров уравнений используют обычно способ наименьших квадратов.

Мы надеемся, что да ли наиболее полное определение и понятие термина аппроксимация, привели ее примеры

Источник

Линейная аппроксимация

При обработке экспериментальных данных часто возникает необходимость аппроксимировать их линейной функцией.

Наиболее часто встречающим видом точечной аппроксимации является интерполяция – нахождение промежуточных значений величины по имеющемуся дискретному набору известных значений.

В случае если между различными узлами полиномы различны, говорят о кусочной или локальной интерполяции.

Найдя интерполяционный полином, мы можем вычислить значения функции между узлами, а также определить значение функции даже за пределами заданного интервала (провести экстраполяцию ).

Аппроксимация линейной функцией

Любая линейная функция может быть записана уравнением

Аппроксимация заключается в отыскании коэффициентов a и b уравнения таких, чтобы все экспериментальные точки лежали наиболее близко к аппроксимирующей прямой.

С этой целью чаще всего используется метод наименьших квадратов (МНК), суть которого заключается в следующем: сумма квадратов отклонений значения точки от аппроксимирующей точки принимает минимальное значение:

Решение поставленной задачи сводится к нахождению экстремума указанной функции двух переменных. С этой целью находим частные производные функции функции по коэффициентам a и b и приравниваем их к нулю.

Решаем полученную систему уравнений

Определяем значения коэффициентов

Для вычисления коэффициентов необходимо найти следующие составляющие:

Тогда значения коэффициентов будут определены как

Пример реализации

Для примера реализации воспользуемся набором значений, полученных в соответствии с уравнением прямой

y = 8 · x — 3

Рассчитаем указанные коэффициенты по методу наименьших квадратов.
Результат сохраняем в форме двумерного массива, состоящего из 2 столбцов.
При следующем запуске программы добавим случайную составляющую к указанному набору значений и снова рассчитаем коэффициенты.

Построение графика функции

Для наглядности построим график функции, полученный аппроксимацией по методу наименьших квадратов. Подробнее о построении графика функции описано здесь.

Аппроксимация с фиксированной точкой пересечения с осью y

В случае если в задаче заранее известна точка пересечения искомой прямой с осью y, в решении задачи останется только одна частная производная для вычисления коэффициента a.

В этом случае текст программы для поиска коэффициента угла наклона аппроксимирующей прямой будет следующий (имя функции getApprox() заменено на getApproxA() во избежание путаницы).

Источник

Что такое аппроксимация

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Многие термины, используемые точными науками, находят свое применение и в обыденной жизни.

Сегодня рассмотрим один из них, термин «аппроксимация».

Узнаем, что такое аппроксимация в математике и в каких ситуациях это понятие можно использовать, исключая точные науки.

Аппроксимация в математике — это …

Как правило, суть термина раскрывается, если его перевести на родной язык. В переводе с латинского «proxima» – это «ближайшая», более широкое толкование перевода – «приближение».

Следовательно, аппроксимация – это метод вычислений, используемый в математике, заключающийся в том, что сложные математические объекты при расчетах (других исследованиях) заменяются более простыми (но максимально похожими).

Пример: при расчетах, в которых используются иррациональные числа (бесконечные десятичные дроби), эти числа заменяются рациональными числами (конечными дробями), приближенными по количественному значению. Этот метод называется диофантовым приближением и является примером применение метода аппроксимации.

Знакомое нам всем число π (пи) – это бесконечная десятичная дробь. π = 3,1415926535897932 …. При вычислениях, в которых используется число «пи», принято брать не дробь целиком (но это и невозможно, ведь она бесконечна), а только 2 цифры после запятой.

Таким образом, принято считать, что π = 3,14. И это тоже применение метода аппроксимации.

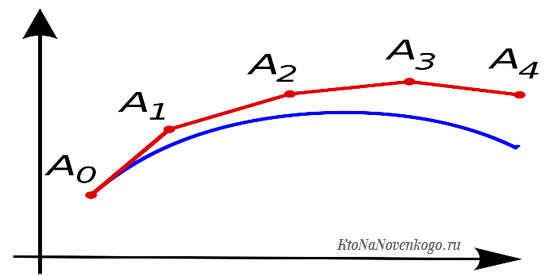
В геометрии метод аппроксимации используется в действиях с кривыми: для удобства вычислений они заменяются ломаными. Как это выглядит, можно посмотреть на схеме:

Кривая (синий цвет) для проведения каких-либо вычислений аппроксимируется в ломаную, каждое из звеньев которой имеет вершины с координатами, максимально приближенными к координатам кривой.

Термин «аппроксимация» схож по сути со следующими математическими понятиями:

Применение термина «аппроксимация» в иных областях

Суть термина применительно к философским категориям остается той же, что и в математике – это указание на приблизительный характер какого-либо процесса, явления.

Аппроксимация в экономике – это метод, используемый в моделировании экономических ситуаций, а именно – замена сложных производственных или иных экономических объектов более простыми (при сохранении основных входных и выходных параметров этих объектов).

Данный метод позволяет решать сложные задачи с помощью «пожертвования» деталями, что делает алгоритм решения (это что?) более простым.

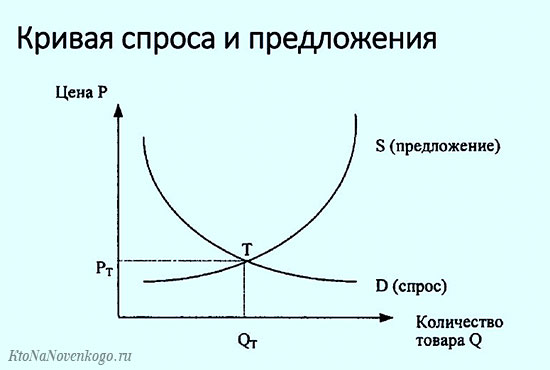
Приведу простой пример: для построения кривых спроса (что это?) и предложения используются показатели цены и количества проданных товаров. Это наглядно изображено на рисунке ниже:

На самом деле на спрос и предложение влияние оказывают и другие факторы.

При проведении анализа эти факторы не учитывают, принимая во внимание только цену и проданный товар, следовательно, построенные кривые являются аппроксимацией более сложных кривых. Но для оценки данной экономической ситуации полученные аппроксимированные графики являются достаточными.

Аппроксимация в повседневной жизни – это обобщение ряда событий, имеющих одинаковый посыл. Например, на вопрос: «Как дела?», мы чаще всего отвечаем: «Нормально, все в порядке».

Это аппроксимация оценки своей жизни, своей деятельности за недавний отрезок времени. На самом деле происходило и плохое, и хорошее, но в целом – «все по среднему», мы не вдаемся в подробности и не рассказываем, что произошло за, допустим, последнюю неделю.

Или еще пример: вчера весь день светило солнце, несколько раз «занавешиваясь» облачками. Но на вопрос о погоде мы ответим, что было солнечно, и не будем рассказывать о ее небольших изменениях, потому что они были недолгими, и не существенными.

Краткое резюме

Мы рассмотрели применение термина «аппроксимация» в различных областях. Следует отметить, что практическое использование аппроксимации в алгебре и геометрии очень специфично, поэтому в этой статье детального разъяснения нет.

Для тех, кто хочет подробней узнать про аппроксимацию функций привожу 2 ссылки: первая – лекция общего характера, другая – монография по этой же теме с прикладным уклоном.

Читайте наш блог, это познавательно!

Автор статьи: Елена Копейкина

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (2)

Мне думается, математики, социологи, маркетологи и проч. знают этот термин. Всем же прочим просто не нужно такое специфическое слово. Ну как его использовать вне профессиональной сферы?

Происхождение этого слова я вижу от английского «approximately», что означает «приблизительно». Оно в свою очередь от другого слова, кстати очень распространенный термин в авиации — «approach», то есть приближение, подход.

Источник