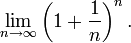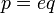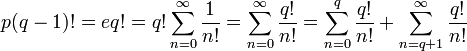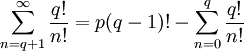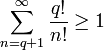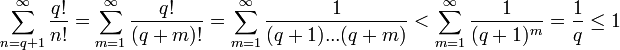что значит большая е в примерах
Экспонента и число е: просто и понятно
Число e всегда волновало меня — не как буква, а как математическая константа. Что число е означает на самом деле?
Разные математические книги и даже моя горячо любимая Википедия описывает эту величественную константу совершенно бестолковым научным жаргоном:
Математическая константа е является основанием натурального логарифма.
Если заинтересуетесь, что такое натуральный логарифм, найдете такое определение:
Натуральный логарифм, ранее известный как гиперболический логарифм, является логарифмом с основанием е, где е – иррациональная константа, приблизительно равная 2.718281828459.
Определения, конечно, правильные. Но понять их крайне сложно. Конечно, Википедия в этом не виновата: обычно математические пояснения сухи и формальны, составляются по всей строгости науки. Из-за этого новичкам сложно осваивать предмет (а когда-то каждый был новичком).
С меня хватит! Сегодня я делюсь своими высокоинтеллектуальными соображениями о том, что такое число е, и чем оно так круто! Отложите свои толстые, наводящие страх математические книжки в сторону!
Число е – это не просто число
Описывать е как «константу, приблизительно равную 2,71828…» — это все равно, что называть число пи «иррациональным числом, приблизительно равным 3,1415…». Несомненно, так и есть, но суть по-прежнему ускользает от нас.
Число пи — это соотношение длины окружности к диаметру, одинаковое для всех окружностей. Это фундаментальная пропорция, свойственная всем окружностям, а следовательно, она участвует в вычислении длины окружности, площади, объема и площади поверхности для кругов, сфер, цилиндров и т.д. Пи показывает, что все окружности связаны, не говоря уже о тригонометрических функциях, выводимых из окружностей (синус, косинус, тангенс).
Число е является базовым соотношением роста для всех непрерывно растущих процессов. Число е позволяет взять простой темп прироста (где разница видна только в конце года) и вычислить составляющие этого показателя, нормальный рост, при котором с каждой наносекундой (или даже быстрее) всё вырастает еще на немного.
Число е участвует как в системах с экспоненциальным, так и постоянным ростом: население, радиоактивный распад, подсчет процентов, и много-много других. Даже ступенчатые системы, которые не растут равномерно, можно аппроксимировать с помощью числа е.
Также, как любое число можно рассматривать в виде «масштабированной» версии 1 (базовой единицы), любую окружность можно рассматривать в виде «масштабированной» версии единичной окружности (с радиусом 1). И любой коэффициент роста может быть рассмотрен в виде «масштабированной» версии е («единичного» коэффициента роста).
Так что число е – это не случайное, взятое наугад число. Число е воплощает в себе идею, что все непрерывно растущие системы являются масштабированными версиями одного и того же показателя.
Понятие экспоненциального роста
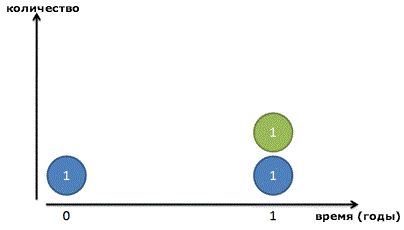
Давайте начнем с рассмотрения базовой системы, которая удваивается за определенный период времени. Например:
И выглядит это примерно так:
Деление на два или удваивание – это очень простая прогрессия. Конечно, мы можем утроить или учетверить, но удваивание более удобно для пояснения.
Математически, если у нас есть х разделений, мы получаем в 2^x раз больше добра, чем было вначале. Если сделано только 1 разбиение, получаем в 2^1 раза больше. Если разбиений 4, у нас получится 2^4=16 частей. Общая формула выглядит так:
Другими словами, удвоение – это 100% рост. Мы можем переписать эту формулу так:
Это то же равенство, мы только разделили «2» на составные части, которыми в сущности и является это число: начальное значение (1) плюс 100%. Умно, да?
Конечно, мы можем подставить и любое другое число (50%, 25%, 200%) вместо 100% и получить формулу роста для этого нового коэффициента. Общая формула для х периодов временного ряда будет иметь вид:
Это просто означает, что мы используем норму возврата, (1 + прирост), «х» раз подряд.
Приглядимся поближе
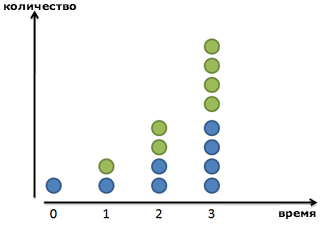
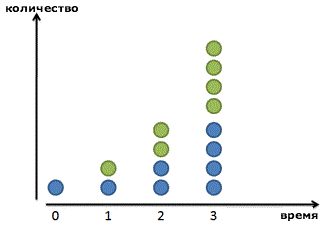
Наша формула предполагает, что прирост происходит дискретными шагами. Наши бактерии ждут, ждут, а потом бац!, и в последнюю минуту они удваиваются в количестве. Наша прибыль по процентам от депозита магическим образом появляется ровно через 1 год. На основе формулы, написанной выше, прибыль растет ступенчато. Зеленые точки появляются внезапно.
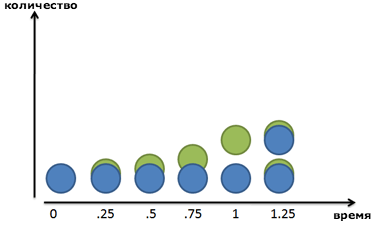
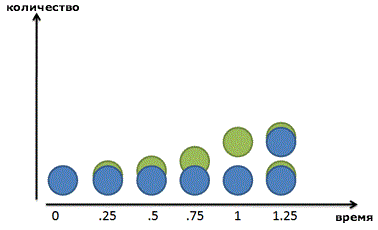
Но мир не всегда таков. Если мы увеличим картинку, мы увидим, что наши друзья-бактерии делятся постоянно:
Зеленый малый не возникает из ничего: он медленно вырастает из синего родителя. После 1 периода времени (24 часа в нашем случае), зеленый друг уже полностью созрел. Повзрослев, он стает полноценным синим членом стада и может создавать новые зеленые клеточки сам.
Эта информация как-то изменит наше уравнение?
Не-а. В случае с бактериями, полусформированные зеленые клетки все же не могут ничего делать, пока не вырастут и совсем не отделятся от своих синих родителей. Так что уравнение справедливо.
E (математическая константа)
Играет важную роль в дифференциальном и интегральном исчислении, а также многих других разделах математики.

Содержание
Способы определения
Число e может быть определено несколькими способами.
Свойства
История
Данное число иногда называют неперовым в честь шотландского учёного Непера, автора работы «Описание удивительной таблицы логарифмов» (1614 год). Однако это название не совсем корректно, так как у него логарифм числа x был равен 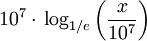
Впервые константа негласно присутствует в приложении к переводу на английский язык вышеупомянутой работы Непера, опубликованному в 1618 году. Негласно, потому что там содержится только таблица натуральных логарифмов, определённых из кинематических соображений, сама же константа не присутствует (см.: Непер).
Предполагается, что автором таблицы был английский математик Отред.
Саму же константу впервые вычислил швейцарский математик Бернулли при анализе следующего предела:
Первое известное использование этой константы, где она обозначалась буквой b, встречается в письмах Лейбница Гюйгенсу, 1690—1691 годы.
Букву e начал использовать Эйлер в 1727 году, а первой публикацией с этой буквой была его работа «Механика, или Наука о движении, изложенная аналитически» 1736 год. Соответственно, e обычно называют числом Эйлера. Хотя впоследствии некоторые учёные использовали букву c, буква e применялась чаще и в наши дни является стандартным обозначением.
Почему была выбрана именно буква e, точно неизвестно. Возможно, это связано с тем, что с неё начинается слово exponential («показательный», «экспоненциальный»). Другое предположение заключается в том, что буквы a, b, c и d уже довольно широко использовались в иных целях, и e была первой «свободной» буквой. Неправдоподобно предположение, что Эйлер выбрал e как первую букву в своей фамилии (нем. Euler ).
Способы запоминания
Доказательство иррациональности
Пускай 
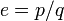
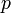
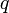
Умножая обе части уравнения на 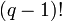
Переносим 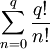
Все слагаемые правой части целые, следовательно:
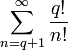
Но с другой стороны
Интересные факты
Число e – его смысл и доказательство сходимости последовательности
Определение числа e
Этот предел является частным случаем второго замечательного предела. Число e иногда называют числом Эйлера или числом Непера. Это самое используемое число в математическом анализе. Оно примерно равно
.
Число e можно представить в виде ряда:
.
Далее приводится объяснение, почему оно так популярно в математике, и дается доказательство существования конечного предела (1).
Смысл числа e
Таким образом, смысл применения числа e заключается в том, что через него выражается производная показательной функции, и без него просто нельзя обойтись.
Доказательство сходимости последовательности
Здесь мы покажем, что последовательность с общим членом
(2)
имеет конечный предел. Для этого мы применим теорему Вейерштрасса о пределе монотонной последовательности. Тогда нам нужно доказать, что
1) последовательность (2) монотонна;
2) последовательность (2) ограничена.
Доказательство можно выполнять различными способами.
Применение бинома Ньютона
Отсюда получаем ограниченность :
.
Поскольку последовательность монотонна и ограничена, то, по теореме Вейерштрасса, она имеет конечный предел.
Применение неравенства Бернулли
Итак, мы показали, что последовательность монотонна и ограничена. Тогда по теореме Вейерштрасса, она имеет конечный предел.
Использование вспомогательной последовательности
Для исследования сходимости исходной последовательности, иногда бывает удобно взять вспомогательную последовательность, которую легче исследовать. При этом предел исходной последовательности должен выражаться через предел вспомогательной.
Поскольку последовательность монотонна и ограничена, то, по теореме Вейерштрасса, она имеет конечный предел.
Элементы исходной последовательности выражаются через :
.
Далее замечаем, что
.
Применяем теорему о пределе частного числовой последовательности:
.
Поскольку последовательность имеет конечный предел, то и исходная последовательность имеет конечный предел.
Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Число Эйлера (e)
Число e (или, как его еще называют, число Эйлера) – это основание натурального логарифма; математическая константа, являющаяся иррациональным числом.
Способы определения числа e (формула):
1. Через предел:
Второй замечательный предел:
Альтернативный вариант (следует из формулы Муавра – Стирлинга):
2. Как сумма ряда:
Свойства числа e
1. Предел обратного числа e
2. Производные
Производной экспоненциальной функции является экспоненциальная функция:
Производной натуральной логарифмической функции является обратная функция:
3. Интегралы
Неопределенный интеграл натуральной логарифмической функции loge x:
Определенный интеграл от 1 до e обратной функции 1/x равен 1:
Логарифмы с основанием e
Натуральный логарифм числа x определяется как базовый логарифм x с основанием e:
Экспоненциальная функция
Это показательная функция, которая определяется следующим образом:
Формула Эйлера
Комплексное число e iθ равняется:
Экспонента и число е: просто и понятно.
Число e всегда волновало меня — не как буква, а как математическая константа. Что число е означает на самом деле?
Разные математические книги и даже моя горячо любимая Википедия описывает эту величественную константу совершенно бестолковым научным жаргоном:
Математическая константа е является основанием натурального логарифма.
Если заинтересуетесь, что такое натуральный логарифм, найдете такое определение:
Натуральный логарифм, ранее известный как гиперболический логарифм, является логарифмом с основанием е, где е – иррациональная константа, приблизительно равная 2.718281828459.
Определения, конечно, правильные. Но понять их крайне сложно. Конечно, Википедия в этом не виновата: обычно математические пояснения сухи и формальны, составляются по всей строгости науки. Из-за этого новичкам сложно осваивать предмет (а когда-то каждый был новичком).
С меня хватит! Сегодня я делюсь своими высокоинтеллектуальными соображениями о том, что такое число е, и чем оно так круто! Отложите свои толстые, наводящие страх математические книжки в сторону!
Число е – это не просто число
Описывать е как «константу, приблизительно равную 2,71828…» — это все равно, что называть число пи «иррациональным числом, приблизительно равным 3,1415…». Несомненно, так и есть, но суть по-прежнему ускользает от нас.
Число пи — это соотношение длины окружности к диаметру, одинаковое для всех окружностей. Это фундаментальная пропорция, свойственная всем окружностям, а следовательно, она участвует в вычислении длины окружности, площади, объема и площади поверхности для кругов, сфер, цилиндров и т.д. Пи показывает, что все окружности связаны, не говоря уже о тригонометрических функциях, выводимых из окружностей (синус, косинус, тангенс).
Число е является базовым соотношением роста для всех непрерывно растущих процессов. Число е позволяет взять простой темп прироста (где разница видна только в конце года) и вычислить составляющие этого показателя, нормальный рост, при котором с каждой наносекундой (или даже быстрее) всё вырастает еще на немного.
Число е участвует как в системах с экспоненциальным, так и постоянным ростом: население, радиоактивный распад, подсчет процентов, и много-много других. Даже ступенчатые системы, которые не растут равномерно, можно аппроксимировать с помощью числа е.
Также, как любое число можно рассматривать в виде «масштабированной» версии 1 (базовой единицы), любую окружность можно рассматривать в виде «масштабированной» версии единичной окружности (с радиусом 1). И любой коэффициент роста может быть рассмотрен в виде «масштабированной» версии е («единичного» коэффициента роста).
Так что число е – это не случайное, взятое наугад число. Число е воплощает в себе идею, что все непрерывно растущие системы являются масштабированными версиями одного и того же показателя.
Понятие экспоненциального роста
Давайте начнем с рассмотрения базовой системы, которая удваивается за определенный период времени. Например:
И выглядит это примерно так:
Деление на два или удваивание – это очень простая прогрессия. Конечно, мы можем утроить или учетверить, но удваивание более удобно для пояснения.
Математически, если у нас есть х разделений, мы получаем в 2^x раз больше добра, чем было вначале. Если сделано только 1 разбиение, получаем в 2^1 раза больше. Если разбиений 4, у нас получится 2^4=16 частей. Общая формула выглядит так:
Другими словами, удвоение – это 100% рост. Мы можем переписать эту формулу так:
Это то же равенство, мы только разделили «2» на составные части, которыми в сущности и является это число: начальное значение (1) плюс 100%. Умно, да?
Конечно, мы можем подставить и любое другое число (50%, 25%, 200%) вместо 100% и получить формулу роста для этого нового коэффициента. Общая формула для х периодов временного ряда будет иметь вид:
Это просто означает, что мы используем норму возврата, (1 + прирост), «х» раз подряд.
Наша формула предполагает, что прирост происходит дискретными шагами. Наши бактерии ждут, ждут, а потом бац!, и в последнюю минуту они удваиваются в количестве. Наша прибыль по процентам от депозита магическим образом появляется ровно через 1 год. На основе формулы, написанной выше, прибыль растет ступенчато. Зеленые точки появляются внезапно.
Но мир не всегда таков. Если мы увеличим картинку, мы увидим, что наши друзья-бактерии делятся постоянно:
Зеленый малый не возникает из ничего: он медленно вырастает из синего родителя. После 1 периода времени (24 часа в нашем случае), зеленый друг уже полностью созрел. Повзрослев, он стает полноценным синим членом стада и может создавать новые зеленые клеточки сам.
Эта информация как-то изменит наше уравнение?
Не-а. В случае с бактериями, полусформированные зеленые клетки все же не могут ничего делать, пока не вырастут и совсем не отделятся от своих синих родителей. Так что уравнение справедливо.
Но деньги меняют все
С деньгами дела обстоят по-другому. Как только мы зарабатываем пару монет прибыли, эти монетки начинают приносить свои микро-прибыли. Нет необходимости ждать, пока набежит целый рубль — свежим денежкам совсем не нужно дозревать, чтобы начать плодоносить.
Основываясь на нашей старой формуле, прирост процента выглядит примерно так:
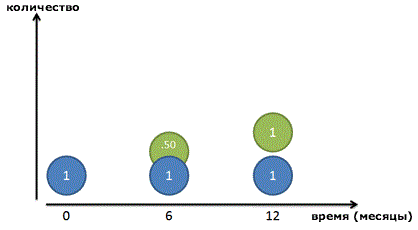
Но опять же, это не совсем правильно: вся сумма процента появляется в последний день. Давайте посмотрим поближе и разделим год на два промежутка. Мы зарабатываем 100% прибыль каждый год, или по 50% каждые 6 месяцев. Таким образом, мы заработаем 50 копеек в первые полгода, и другие 50 копеек во вторую половину года:
И все равно, это неверно! Конечно, наш рубль-родитель (Синий кружок) зарабатывает рубль в течение года. Но после 6 месяцев мы получим 50-копеечный кусочек прибыли – готовые деньги, которыми мы пренебрегаем! Эти 50 копеек уже могли бы зарабатывать свои собственные деньги:
Поскольку наш коэффициент равен 50% каждые полгода, эти 50 копеек могли бы заработать еще 25 копеек (50% от 50 копеек). В конце года мы бы получили:
Если все сложить, получится 2,25 рублей. Мы заработали 1,25 рубля всего на одном исходном рубле, и это даже лучше, чем удвоение!
Вернемся к формуле. Рост за два полу-периода по 50% составит:
Переходим на составной рост
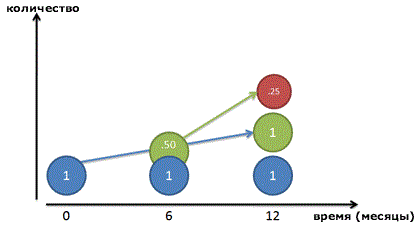
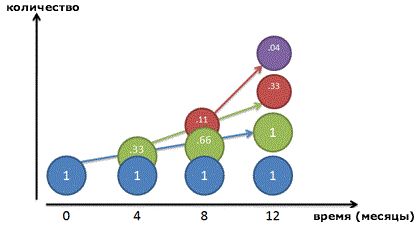
Идем дальше. Давайте поделим рост не на два периода по 50%, а на 3 сегмента по 33% каждый. Кто сказал, что надо ждать целых 6 месяцев до начала получения прибыли? Давайте детализируем наши вычисления.
Вот так выглядит наш рост, расписанный на 3 составных периода:
Фуух! Спустя 12 месяцев у нас получается: 1 + 1 + 0.33 + 0.04 или примерно 2.37 рубля.
Потратим еще чуть времени, чтобы понять, что на самом деле происходит с таким ростом:
Теперь понятнее? Поначалу это сложно — я и сам запутался, пока рисовал все эти графики. Главное понять, что каждый «рубль» создает маленьких помощников, а те, в свою очередь, создают помощников себе, и так далее.
Если рассматривать год как 3 равных периода, формула роста будет такой:
рост = (1 + 100%/3) 3 = 2.37037.
Мы заработали 1.37 рубля, а это даже лучше, чем те 1.25, что получились у нас в предыдущий раз!
Можно ли преумножать деньги бесконечно?
А почему бы не разбить год на более короткие периоды? Как насчет месяца, дня, часа или даже наносекунды? Наша прибыль взлетит до небес?
Прибыль увеличится, но уже не намного. Попробуем подставить в нашу волшебную формулу разные значения n, и получим следующее: