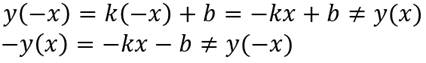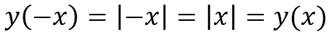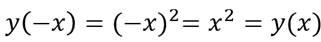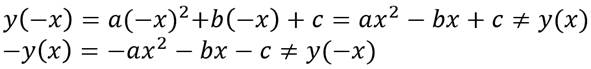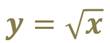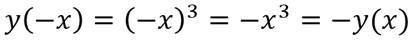что значит четная нечетная функция
Четные и нечетные функции
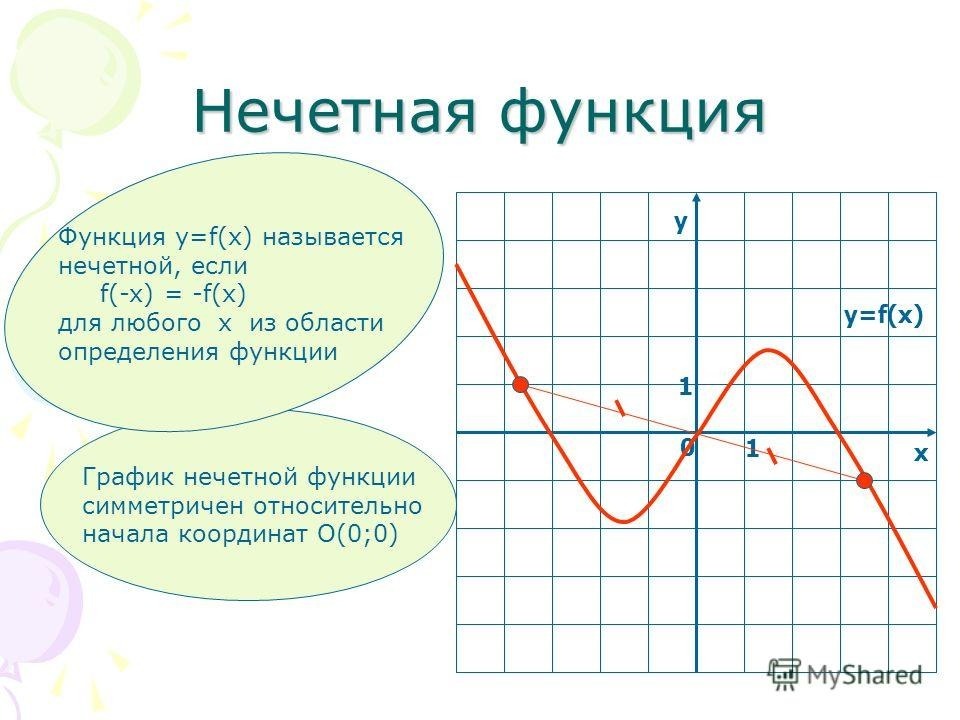
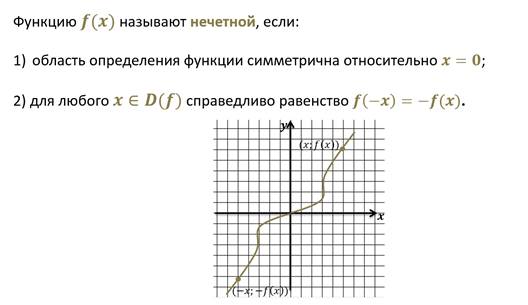
Нечётная фу́нкция — функция, меняющая знак при изменении знака независимого переменного.
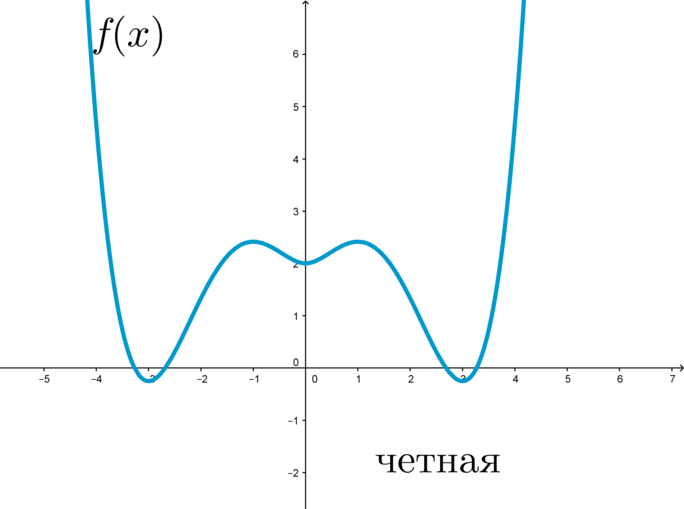
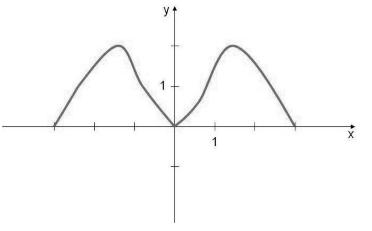
Чётная фу́нкция — это функция, не изменяющая своего значения при изменении знака независимого переменного.
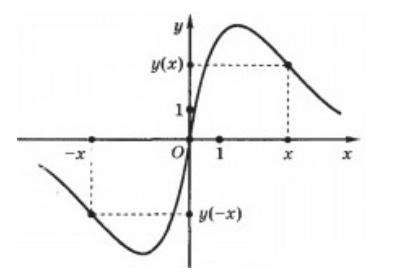
Нечётная фу́нкция — функция, симметричная относительно центра координат, а чётная — функция, симметричная относительно оси ординат.
Содержание
Определения
Свойства
Примеры
Нечётные функции
Чётные функции
Вариации и обобщения
Полезное
Смотреть что такое «Четные и нечетные функции» в других словарях:
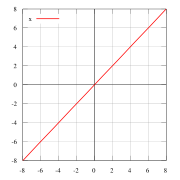
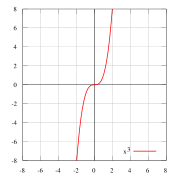
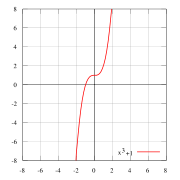
Нечетные и четные функции — f(x) = x пример нечётной функции. f(x) = x2 пример чётной функции. f(x) = x3 … Википедия
Земляков — Земляков, Александр Николаевич Файл:Zemlyakov.jpg Александр Николаевич Земляков (17 апреля 1950(19500417), Бологое 1 января 2005, Черноголовка) математик,выдающийся советский и российский педагог, автор учебно педагогической… … Википедия
Земляков, Александр Николаевич — Александр Николаевич Земляков (17 апреля 1950(19500417), Бологое 1 января 2005, Черноголовка) математик, выдающийся советский и российский педагог, автор учебно педагогической литературы. Биография Закончил в 1967 году с золотой… … Википедия
Ряд Фурье — Добавление членов ряда Фурье … Википедия
H.265 — или HEVC (англ. High Efficiency Video Coding высокоэффективное видеокодирование) предполагаемая будущая рекомендация ITU T и проект стандарта ISO/IEC по сжатию видео с применением более эффективных алгоритмов по сравнению с H.264/MPEG… … Википедия
МАРЦИАН КАПЕЛЛА — МАРЦИАН КАПЕЛЛА (Martianus Minneius Felix Capeila) (2 я пол. 5 в. н. э.), латинский платоник, последний латинский выразитель «религии культуры» спасения через пайдейю. Известен как автор сочинения «О браке Филологии и Меркурия» (De nuptiis… … Античная философия
Link 16 — (TADIL J) тип военной тактической сети обмена данных, близкому к реальному. Используется США и странами НАТО. Является одной из составных частей семейства тактических сетей передачи данных TADIL (англ. Tactical Digital Information Link … Википедия
ЛАНДАУ ТЕОРЕМЫ — теоремы для регулярных в круге функций, устанавливающие нек рые связи между геометрич. свойствами производимого этими функциями конформного отображения и начальными коэффициентами представляющих их степенных рядов. В 1904 Э. Ландау показал [1],… … Математическая энциклопедия
Четные и нечетные функции
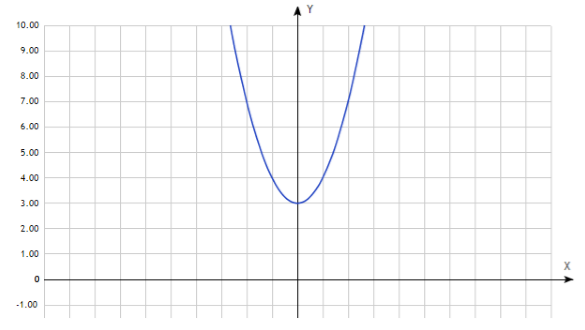
График четной функции симметричен относительно оси \(y\) :
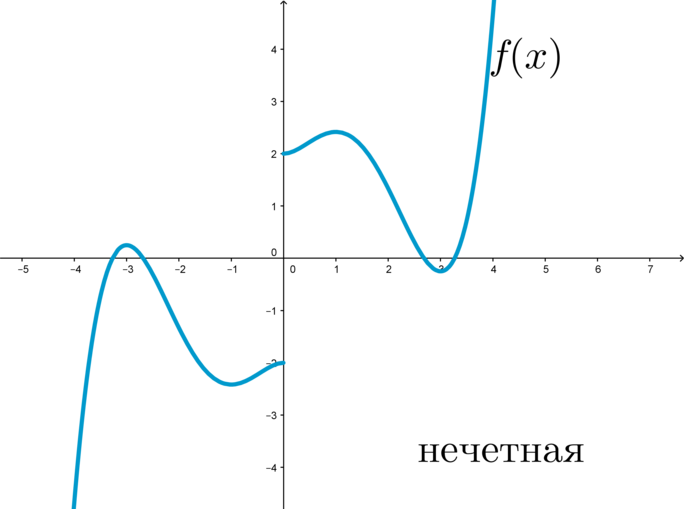
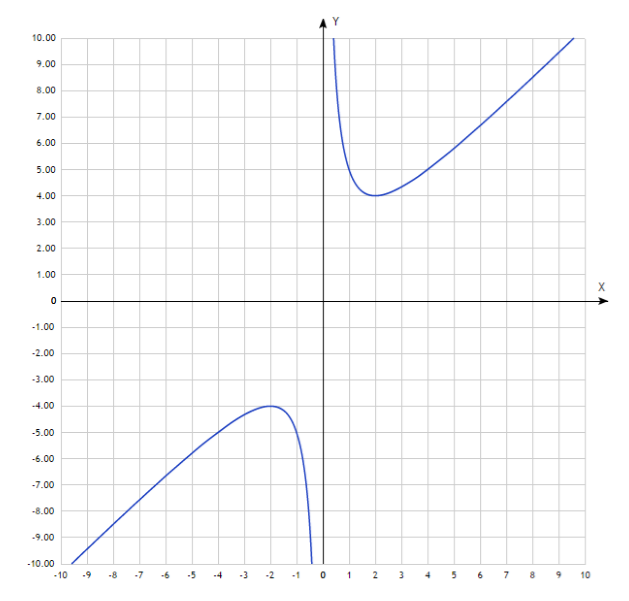
График нечетной функции симметричен относительно начала координат:
\(\blacktriangleright\) Функции, не являющиеся ни четными, ни нечетными, называются функциями общего вида. Такую функцию можно всегда единственным образом представить в виде суммы четной и нечетной функции.
\(\blacktriangleright\) Некоторые свойства:
1) Произведение и частное двух функций одинаковой четности — четная функция.
2) Произведение и частное двух функций разной четности — нечетная функция.
3) Сумма и разность четных функций — четная функция.
4) Сумма и разность нечетных функций — нечетная функция.
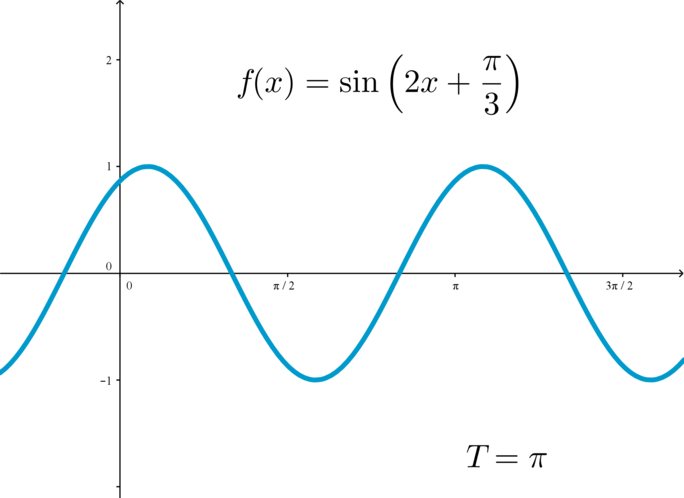
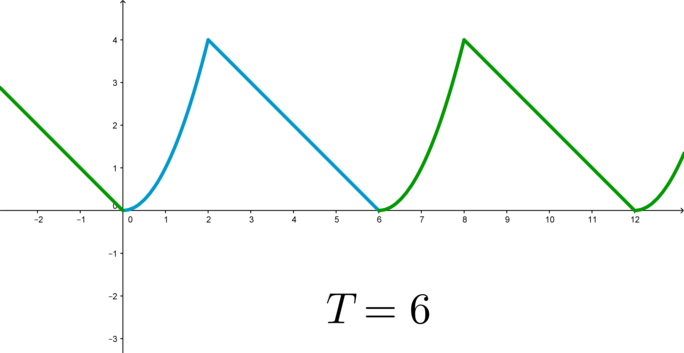
Для того, чтобы построить график периодической функции, можно построить ее график на любом отрезке длиной \(T\) (главный период); тогда график всей функции достраивается сдвигом построенной части на целое число периодов вправо и влево:
При каких значениях параметра \(a\) уравнение
имеет единственное решение?
\[2\cdot 0+a\mathrm
симметричен относительно начала координат.
Если график функции симметричен относительно начала координат, то такая функция является нечетной, то есть выполнено \(f(-x)=-f(x)\) для любого \(x\) из области определения функции. Таким образом, требуется найти те значения параметра, при которых выполнено \(f(-x)=-f(x).\)
\(\dfrac n2, n\in\mathbb
(Задача от подписчиков)
имеет хотя бы один корень.
(Задача от подписчиков)
имеет шесть различных решений.
Таким образом, план решения становится ясен. Давайте по пунктам выпишем условия, которые должны выполняться.
1) Чтобы уравнение \((*)\) имело два различных решения, его дискриминант должен быть положительным: \[D=a^2-16a+52>0\quad\Leftrightarrow\quad a\in (-\infty;8-2\sqrt3)\cup(8+2\sqrt3;+\infty)\]
2) Также нужно, чтобы оба корня были положительными (так как \(t>0\) ). Если произведение двух корней положительное и сумма их положительная, то и сами корни будут положительными. Следовательно, нужно: \[\begin
Понятие четной и нечетной функции
Понятие четности и нечетности функции
Главное условие при исследовании функции на четность/нечетность — это симметричность области определения относительно 0. Если она не симметрична, то функция не является ни четной, ни нечетной, и дальнейшее исследование производить не нужно. Например, \(D(y)\in(-\infty;+\infty)\) симметрична относительно 0, а \(D(y):x\in(-5;9)\) — нет.
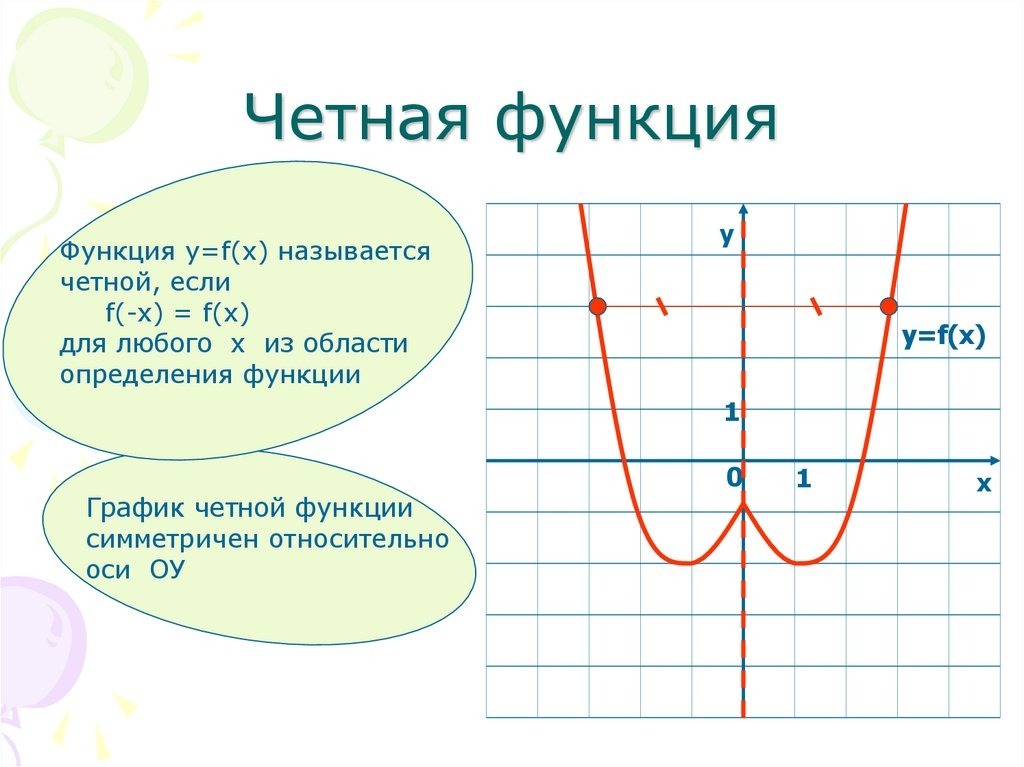
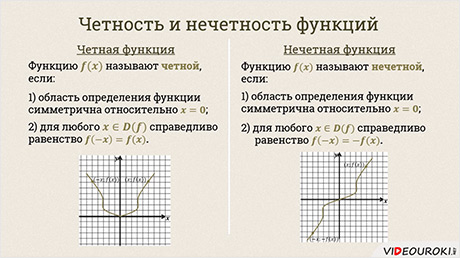
Четная функция
Функцию \(f(x)\) называют четной, если для любого значения х из области определения функции \(f(x)\) соблюдается равенство \(f(-x)=f(x).\)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
График четной функции симметричен относительно оси Ох.
Нечетная функция
Функцию \(f(x)\) называют нечетной, если для любого значения х из области определения функции \(f(x)\) соблюдается равенство \(f(-x)=-f(x).\)
График нечетной функции симметричен относительно начала координат (точки (0;0)).
Произведение четной и нечетной функции
Произведение четной и нечетной функций есть нечетная функция.
Пусть \(f(x)\) — четная функция, а \(g(x)\) — нечетная. Тогда \(f(x)=f(-x), а g(-x)=-g(x).\)
Исследование функций в примерах
Доказать, что функция \(y=x^2\) четная.
1. Найдем область определения: \(D(y):x\in(-\infty;+\infty)\) — симметрична относительно 0.
Исследовать на четность и нечетность функцию \(f(x)=8x^3-7x.\)
1. Найдем область определения: \(D(f):x\in(-\infty;+\infty)\) — симметрична относительно 0.
Исследовать на четность и нечетность функции \(f_1(x)=\frac
Рассмотрим первую функцию:
1. Найдем область определения: x — любое число, кроме 1. Она не симметрична относительно 0, значит \( f_1(x)\) относится к функциям общего вида, то есть не является ни четной ни нечетной.
Рассмотрим вторую функцию:
Четные и нечетные функции
Вы будете перенаправлены на Автор24
Четные функции
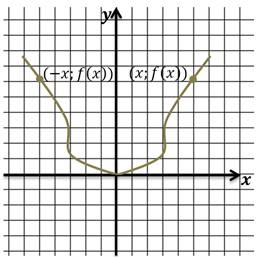
Так как при выборе равных по модулю с обоими знаками значений независимых переменных для любой четной функции значения самой функции будет совпадать, то график этих функции будет подчиняться закону осевой симметрии по отношению к оси ординат (рис. 1).
Нечетные функции
Так как при выборе равных по модулю с обоими знаками значений независимых переменных для любой четной функции значения самой функции будут также совпадать по модулю и отрицательны по знакам, то график этих функции будет подчиняться закону центральной симметрии по отношению к началу координат (рис. 2).
Готовые работы на аналогичную тему
Функция общего вида
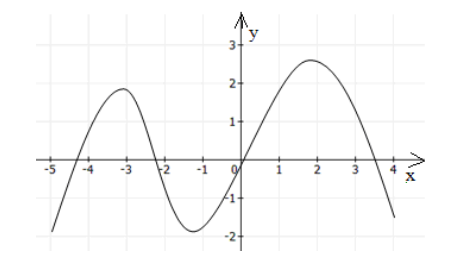
Функция общего вида никогда не будет симметрична оси ординат и началу координат. Пример функции общего вида изображен на рисунке 3.
Пример задачи
Исследовать функцию на четность и нечетность и построить их графики.
Изобразим её на графике:
Изобразим её на графике:
Четность и нечетность функций
Урок 41. Подготовка к ОГЭ по математике 9 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Четность и нечетность функций»
· повторить такое свойство функции, как чётность и нечётность.
Прежде давайте вспомним свойства функций, о которых мы уже говорили. Это: область определения функции, область значений функции, нули функции, промежутки знакопостоянства функции, промежутки монотонности функции.
Для того чтобы мы могли говорить о чётности, еще раз давайте повторим, что мы понимаем под областью определения функции.
Область определения функции – это все значения, которые может принимать аргумент.
Теперь вспомним, что
Теперь давайте разберёмся с этим определением по подробней. Первым условием является то, что область определения функции должна быть симметрична относительно икс равного нулю. Что это значит? Это значит, что если число А принадлежит области определения, то и число минус А тоже принадлежит области определения этой функции.
Второе условие чётности говорит о том, что:
Если посмотреть на график чётной функции, то можно увидеть, что он будет симметричен относительно оси ординат.
Если же нарушается первое условие, то есть область определения функции – не симметричное относительно x = 0 множество, то такая функция не обладает свойством чётности.
Теперь давайте вспомним какую функцию называют нечётной.
Если мы посмотрим на график нечётной функции, то нетрудно увидеть, что он симметричен относительно начала координат.
Мы с вами уже рассмотрели некоторые элементарные функции, их свойства и графики. А теперь давайте попробуем определить какие из этих функций являются чётными, нечётными, ни чётными, ни нечётными.
Если мы посмотрим на графики прямой пропорциональности, то увидим, что эти графики симметричны относительно начала координат.
Теперь давайте рассмотрим обратную пропорциональность.
Область определения этой функции – симметричная относительно x = 0 область, то есть говорить о чётности или нечётности этой функции можно.
Следующей мы рассмотрим линейную функцию.
То есть линейная функция не является ни чётной, ни нечётной.
Рассмотрим функцию y = │x│.
Тогда получим, что функция игрек равно модуль икс – чётная функция.
Область определения – вся числовая прямая.
то есть функция чётная.
Рассмотрим квадратичную функцию.
Область определения – вся числовая прямая.
то есть квадратичная функция не является ни чётной, ни нечётной.
Теперь давайте рассмотрим функцию:
Область определения функции – промежуток [0; + ∞) – это не симметричное относительно точки x = 0 множество, то есть мы сразу можем написать, что о чётности или нечётности этой функции говорить нельзя.
то есть перед нами нечётная функция.
Теперь давайте решим несколько заданий.
Рассмотрим ещё один пример.
Сегодня на уроке мы повторили такое свойство функций как чётность. Вспомнили какая функция называется чётной, а какая – нечётной.