что значит функция задана неявно
Неявные функции
Неявные функции, определяемые одним уравнением.
Пусть функция \(F(x,y)\) определена в \(R^2\). Рассмотрим уравнение
$$
F(x,y)=0.\label
$$
Множество \(G_F\) точек плоскости, координаты которых удовлетворяют уравнению \eqref
Так, график уравнения \(x^2 + y^2 — 1 = 0\) есть окружность, график уравнения \((x-1)(x+y-1)=0\) есть пара прямых \(x = 1\) и \(x+y-1=0\) (рис. 28.1).
Рис. 28.1
Если график \(G_F\) уравнения \eqref
Меняя местами переменные \(x\) и \(y\), можно говорить о том, что уравнение \eqref
Докажем теорему, дающую достаточные условия существования, непрерывности и дифференцируемости неявной функции, определяемой уравнением \eqref
Тогда существует прямоугольник
$$
K = \<(x,y): \; x_0-a\leq x\leq x_0+a, \; y_0-b\leq y\leq y_0+b\>,\nonumber
$$
в котором уравнение \(F(x,y) = 0\) определяет \(y\) как неявную функцию \(x\). Функция \(y=f(x)\) непрерывно дифференцируема на интервале \((x_0-a,x_0+a)\) и
$$
f'(x)=-\frac
$$
\(\circ\) Разобьем доказательство на два пункта.
Доказательство существования неявной функции. Из условия \(F_y(x_0,y_0)\neq 0\) следует, что либо \(F_y(x_0,y_0) > 0\), либо \(F_y(x_0,y_0) 0.\label
$$
Если \(F_y(x_0,y_0) 0\).
Так как функция \(F_y(x,y)\) в точке \((x_0,y_0)\) непрерывна и в силу условия \eqref
$$
K_1=\<(x,y): \; |x-x_0|\leq a_1, \; |y-y_0|\leq b\>,\nonumber
$$
в котором функция \(F_y(x,y) > 0\).
Рис. 28.3
Рассмотрим функцию одной переменной
$$
\psi (y)=F(x_0,y),\quad y_0-b\leq y\leq y_0+b.\nonumber
$$
Функция \(\psi (y)\) строго возрастает на отрезке \([y_0-b,y_0+b]\), так как
$$
\psi'(y)=F_y(x_0,y) > 0.\nonumber
$$
Кроме того, в силу условия \(F(x_0,y_0)=0\)
$$
\psi (y_0) = F(x_0,y_0) = 0.\nonumber
$$
Поэтому
$$
\psi (y_0-b)= F(x_0,y_0-b) 0.\label
$$
Неравенства \eqref
$$
F(x,y_0-b) 0.\label
$$
Покажем, что в прямоугольнике
$$
K=\<(x,y): \; |x-x_0|\leq a, \; |y-y_0|\leq b\>,\nonumber
$$
уравнение \(F(x,y) = 0\) определяет \(y\) как неявную функцию \(x\).
Возьмем любую точку \(x^*\in [x_0-a,x_0+a]\) и рассмотрим непрерывную на отрезке \([y_0-b,y_0+b]\) функцию одной переменной \(\varphi (y)=F(x^*,y)\). В силу условия \eqref
$$
\varphi(y_0-b)= F(x^*,y_0-b) 0.\nonumber
$$
По теореме Коши о промежуточных значениях найдется такая точка \(y^*\in [y_0-b,y_0+b]\), что
$$
\varphi(y^*) = F(x^*,y^*)=0.\nonumber
$$
Так как \(\varphi'(y) = F_y(x^*,y) > 0\), то функция \(\varphi(y)\) строго возрастает на отрезке \([y_0-b,y_0+b]\) и не может обратиться на этом отрезке в нуль более одного раза.
Таким образом, для любого \(x\in [x_0-a,x_0+a]\) найдется единственный \(y\in [y_0-b,y_0+b]\) такой, что \(F(x,y) = 0\). Это означает, что в прямоугольнике \(K\) уравнение \(F(x,y) = 0\) определяет \(y\) как неявную функцию \(x\).
Доказательство непрерывной дифференцируемости неявной функции. Непрерывная на замкнутом прямоугольнике \(K\) функция \(F_y(x,y)\) по теореме Вейерштрасса принимает на этом прямоугольнике свое наименьшее значение \(\alpha\). Так как \(F_y(x,y) > 0\) на \(K\), то
$$
F_y(x,y)\geq a > 0,\qquad (x,y)\in K.\label
$$
Непрерывная на \(K\) функция \(F_x(x,y)\) ограничена на \(K\). Поэтому
$$
|F_x(x,y)| Замечание 1.
Если известно, что уравнение \(F(x,y)=0\) определяет в прямоугольнике \(a\leq x\leq b, \; c\leq y\leq d\) переменную \(y\) как неявную функцию \(x\), то связь между \(dy\) и \(dx\) можно установить, формально дифференцируя тождество \(F(x,y(x)) = 0\). Воспользовавшись инвариантностью формы дифференциала, получаем
$$
F_x(x,y)dx + F_y(x,y)dy = 0.\nonumber
$$
Дифференцируя последнее тождество еще раз, можем найти второй дифференциал \(d^2y\)
$$
F_
$$
Неявные функции, определяемые системой уравнений.
Рассмотрим систему \(m\) уравнений с \(n+m\) неизвестными
$$
\left\<\begin
$$
При формулировке общей теоремы о неявных функциях удобно пользоваться понятием декартова произведения множеств. Если \(A\) и \(B\) — произвольные множества, то их декартово произведение \(A\times B\) есть множество пар \((x,y)\), где \(x\in A\), \(y\in B\). Так, декартово произведение \([a,b]\times [c,d]\) есть множество пар вещественных чисел таких, что \(a\leq x\leq b,\) и \(c\leq y\leq d\), то есть прямоугольник в \(R^2\).
Легко видеть, что в том случае, когда \(K_1(x^0)\subset R^n\) и \(K_2(y^0)\subset R^m\) — клеточные окрестности, их декартово произведение \(K_1(x^0)\times K_2(y^0)\) есть клеточная окрестность точки \((x^0,y^0)=(x_1^0,…,x_n^0,y_1^0,…,y_m^0\) в пространстве \(R^
Для дальнейшего удобно преобразовать переменные, полагая \(x=(x_1,…,x_n), \; y=(y_1,…,y_m)\), где \(y_1=x_
Тогда систему уравнений \eqref
$$
F_i(x,y) = 0, \; i=\overline<1,m>.\label
$$
Функции \(F_i(x,y) = 0\) будем считать определенными в некоторой клеточной окрестности точки \((x^0,y^0)\).
Пусть \(K(x^0)\subset R^n\) и \(Q(y_0)\subset R^m\) есть клеточные окрестности. Будем говорить, что система уравнений \(F_i(x,y)=0, \; i=\overline<1,m>\), определяет в \(K(x^0)\times Q(y_0)\) переменные \(y_1,…,y_m\) как неявные функции переменных \(x_1,…,x_n\), если для любого \(x\in K(x^0)\) найдется единственный \(y\in Q(y^0)\) такой, что \(F_i(x,y) = 0, \; i=\overline<1,m>\).
Пусть выполнены следующие условия:
Тогда найдутся клеточные окрестности \(K(x^0) \subset R^n\) и \(Q(y^0) \subset R^m\) такие, что в \(K(x^0)\times Q(y^0)\) система уравнений \eqref
\(\circ\) Воспользуемся методом индукции по числу уравнений \(m\). При \(m=1\) доказательство теоремы 2 не отличается от доказательства теоремы 1 (в дальнейшем будем ссылаться на этот частный случай теоремы 2 как на теорему 1).
Предположим, что утверждение теоремы верно в том случае, когда система \eqref
Так как определитель \eqref
$$
<\begin
$$
(Здесь и в дальнейшем символ \(0\) означает, что значение соответствующей функции берется для аргументов с верхним индексом \(0\)).
Тогда в силу индукции найдутся такие клеточные окрестности
$$
\begin
Существует несколько способов доказательства теоремы о неявных функциях. Предложенный способ является, по-видимому, наиболее простым, но обладает двумя недостатками: не дает алгоритма для вычисления неявной функции и не обобщается на бесконечномерный случай.
Локальная обратимость регулярного отображения.
Пусть на множестве \(E\subset R^n\) заданы \(n\) функций
$$
f_1(x),…,f_n(x).\nonumber
$$
Они задают отображение \(f: \; E\rightarrow R^n\), которое каждой точке \(x\in E\) ставит в соответствие точку \(y=f(x)\), где
$$
y_1=f_1(x),\quad,…,\quad y_n=f_n(x).\nonumber
$$
Точка \(y=f(x)\) называется образом точки \(x\) при отображении \(f\). Точка \(x\) называется прообразом точки \(y\).
Если \(\Omega\subset E\), то множество
$$
f(\Omega)=\
$$
называется образом множества \(\Omega\) при отображении \(f\). Если \(\omega\subset f(E)\), то множество
$$
f^<-1>(\omega)=\
$$
называется прообразом множества \(\omega\).
Пусть \(G \subset R^n\) есть открытое множество. Отображение \(f: \; G\rightarrow R^n\) называется непрерывным в точке \(x^0\), если \(\forall \varepsilon > 0 \; \exists\delta > 0\) такое, что \(\forall x\) таких, что \(\rho(x,x^0) Лемма 1.
Если \(G\) есть открытое множество, а \(f: \; G\rightarrow R^n\) — непрерывное отображение, то прообраз каждого открытого множества \(\omega\in f(G)\) есть открытое множество.
\(\circ\) Пусть \(\Omega= f^<-1>(\omega)\). Возьмем любую точку \(x^0\in\Omega\). Тогда \(f(x^0)=y^0\in \omega\). Так как множество \(\omega\) открыто, то найдется окрестность \(S_<\varepsilon>(y^0)\in \omega\). В силу непрерывности отображения \(f\) в точке \(x^0\) найдется шаровая окрестность \(S_<\delta>(x^0)\), для которой выполнено условие \eqref
Следовательно,
$$
S_<\delta>(x^0)\subset f^<-1>(\omega)\subset\Omega,\nonumber
$$
и \(\Omega\) — открытое множество. \(\bullet\)
Как обычно, под окрестностью \(A(x^0)\) точки \(x^0\) будем понимать любое множество \(A\), для которого точка \(x^0\) внутренняя.
Пусть \(G \subset R^n\) — открытое множество. Отображение \(f: \; G\rightarrow R^n\) будем называть непрерывно дифференцируемым, если функции \(f_1(x),…,f_n(x)\), задающие это отображение, непрерывно дифференцируемы в \(G\). Непрерывно дифференцируемое отображение \(f: \; G\rightarrow R^n\) будем называть регулярным, если в области \(G\) якобиан отображения \(j_f(x)\neq 0\). Якобианом отображения \(j_f(x)\) называется следующий функциональный определитель:
$$
j_f(x)=\begin
$$
Пусть \(G\) — открытое множество в \(R^n\), а отображение \(f: \; G\rightarrow R^n\) регулярно. Тогда в каждой точке \(x^0\in G\) оно локально регулярно обратимо, то есть \(\forall x^0\in G\) найдутся такие окрестности \(A(x^0) \subset G\) и \(B(y^0)\subset f(G)\), где \(y^0= f(x^0)\), что отображение \(f: \; A(x^0)\rightarrow B(y^0)\) будет взаимно однозначным, причем обратное отображение \(f^<-1>: \; B(y^0)\rightarrow A(x^0)\) регулярно.
\(\circ\) Рассмотрим в \(G\times R^n\) систему уравнений
$$
F_i(x,y)\equiv y_i-f_i(x)=0,\quad i=\overline<1,n>.\label
$$
Пусть \(x^0\) — произвольная точка множества G и \(y^0=f(x^0)\). Тогда функции \(F_i(x,y)\) непрерывно дифференцируемы в \(G\times R^n\) и \(y_i^0= f_i(x^0), \; i=\overline<1,n>\). Так как отображение \(f\) регулярно, то Если \(f: \; G\rightarrow R^n\) есть регулярное отображение, то образ любого открытого множества \(\Omega\subset G\) есть открытое множество. \(\circ\) Пусть \(\omega=f(\Omega)\). Возьмем произвольную точку \(y^0\in\omega\) и пусть \(x^0\) есть какой-то ее прообраз. Тогда, вследствие теоремы 3, найдутся такие окрестности \(A(x^0) \subset \Omega\) и \(B(y^0) \subset \omega\); что отображение \(f: \; A(x^0)\rightarrow B(y^0)\) регулярно обратимо. Поэтому каждая точка \(y^0\in\omega\) принадлежит \(\omega\) вместе с некоторой окрестностью \(B(y^0)\). Множество \(\omega=f(\Omega)\) открыто. \(\bullet\) ПРИМЕР 1. Построение графиков неявных функций одной переменной. Неявная функция многих переменных. Аналогично рассматривают функции многих переменных, заданные неявно. Например, при выполнении соответствующих условий, уравнение Производная неявной функции. При вычислении производной неявной функции воспользуемся правилом дифференцирования сложной функции. Продифференцируем уравнение ПРИМЕР 2. Вычисление производных функций, заданных неявно. Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter Предположим, что значения двух переменных х и у связаны между собой уравнением, которое, если все члены его перенести налево, в общем случае имеет вид имеет место уже тождественно относительно х. Возьмем, например, уравнение оно, очевидно, определяет у как двузначную функцию от х в промежутке И, если вместо у подставить в уравнение (1а) эту функцию, то получится тождество. Здесь удалось найти для у очень простое аналитическое выражение через х, даже в элементарных функциях. Так обстоит дело далеко не всегда. Если взять уравнение которое нам уже встречалось [при других лишь обозначениях переменных, 83], то мы знаем, что этим уравнением у определяется как однозначная функция от х, хотя в конечном виде она через элементарные функции и не выражается. Функция Сейчас нас будет интересовать лишь вопрос о существовании и однозначности теявнот функции (равно как и о других ее свойствах), независимо от возможности представить ее в «явном» виде аналитической формулой. Впрочем, в этой постановке вопрос для нас не нов; с частным случаем его мы имели дело, когда речь шла о существовании и о свойствах обратной функции, и уравнением переменная х определялась как «неявная» функция от у. Поучительна геометрическая трактовка указанного вопроса. Уравнение (1), при известных условиях, выражает кривую на плоскости [например, уравнение (1а), как известно, выражает эллипс (рис. 111)]; в этом случае оно называется неявным уравнением кривой. Вопрос заключается в том, может ли кривая (1) (или ее часть) быть выражена обычным уравнением вида Если мы желаем иметь однозначную функцию, то как видно на примере того же эллипса, нужно ограничить не только область изменения х, но и область изменения у. Мы будем говорить, для краткости, что в прямоугольнике функцию от х, если при каждом значении х в промежутке Обычно нас будет интересовать определенная точка Определение. Функция называется явной, если она задана формулой, правая часть которой не содержит зависимой переменной. Такая функция имеет вид: Например, Определение. Неявной функцией y независимой переменной х называется функция, значения которой находятся из уравнения, связывающего х и y и, не разрешенного относительно y. Неявная функция имеет вид: Например, Замечание. Термины «явная функция» и «неявная функция» характеризуют не природу функции, а способ ее задания. Основные характеристики функции Изучить функцию – это значит охарактеризовать ход ее изменения (ее поведение) при изменении независимой переменной. Характеризуют функцию по следующим свойствам: 1) четность или нечетность функции; 2) периодичность функции; 4) возрастание или убывание функции (монотонность функции); 5) ограниченность функции. Рассмотрим эти характеристики. Четные и нечетные функции Определение. Функция Например, График четной функции расположен симметрично относительно оси Определение. Функция Например, График нечетной функции расположен симметрично относительно начала координат (рис.1.5). Функция может быть ни четной. ни нечетной, и в этом случае её называют функцией общего вида. Например, Графики таких функций не симметричны ни относительно оси Периодические функции Определение. Функция Наименьшее из положительных чисел Т, удовлетворяющих условию определения, называется периодом функции Например, функции Нули функции Определение. Значение аргумента, при котором функция обращается в нуль, Например, нулями функции Монотонные функции Определение. Функция называется возрастающей (убывающей) в некоторой области изменения аргумента, если большему значению аргумента соответствует большее (меньшее) значение функции (рис.1.6, 1.7). Определение. Если функция в некоторой области изменения аргумента является только возрастающей или только убывающей, то функция называется монотонной. Ограниченные функции Определение. Функция Например, функции График ограниченной функции лежит между прямыми УПРАЖНЕНИЯ 1. Найти область определения следующих функций: 1) 2) 3) 4) 2. Найти множество значений функции: 1) 2) 3) 3. Найти Ответ: 4. Пусть Ответ: 5. Установить чётность или нечётность функции: 1) 2) 3) 4) 6. Найти основные периоды функций: 1) 2) 3) 7. Введя промежуточные аргументы, представить данную функцию, как суперпозицию других функций: 1) 2) 8. Для данных функций найти явные обратные: 1) 2) 3)
$$
<\begin
$$
Для системы уравнений \eqref
$$
\begin
$$
что в \(K(x^0)\times Q(y^0)\) система уравнений \eqref
$$
\begin
$$
Пусть \(B(y^0)\) есть внутренность \(Q(y^0)\):
$$
B(y^0) = \left\Что значит функция задана неявно
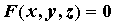
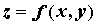
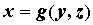
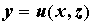
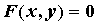
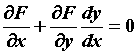
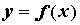
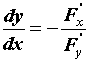
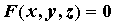
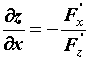
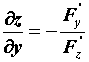
Что значит функция задана неявно









Явные и неявные функции













































































































