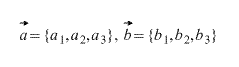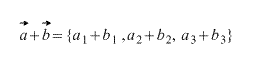что значит геометрическая сумма
Сложение векторов. Векторная сумма. Правила сложения векторов. Геометрическая сумма. Он-лайн калькулятор.
Сложение векторов. Векторная сумма. Правила сложения векторов. Геометрическая сумма. Он-лайн калькулятор
Покоординатное сложение векторов.
Тогда координаты вектора, получившегося при сложении этих двух векторов вычисляются по формуле:
В двумерном случае все абсолютно анологично, просто отбрасываем третью координату.
Теперь перейдем к геометрическому смыслу сложения двух векторов:
При сложении векторов нужно учитывать и их числовые значения, и направления. Есть несколько широко используемых методов сложения:
Правило параллелограмма. Сложение векторов по правилу параллелограмма.
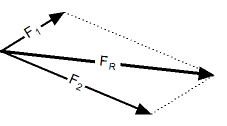
Процедура сложения векторов по правилу параллелограмма заключается в следующем:
Правило треугольника. Сложение векторов по правилу треугольника.

Сложение векторов по правилу треугольника заключается в следующем:
Тригонометрический способ. Сложение векторов тригонометрическим способом.
Сила 1 равна 5кН и воздействует на тело в направлении, на 80 o отличающемся от направления действия второй силы, равной 8 кН.
Результирующая сила вычисляется следующим образом:
Угол между результирующей силой и первой силой равен:
А угол между второй и результирующей силой можно посчитать следующим образом: as
Он-лайн калькулятор сложения векторов.
Калькулятор ниже может быть использован для любвых векторных величин ( силы, скорости и т.д.) Точка начала вектора совпадает с началами обоих исходных векторов.
Консультации и техническая
поддержка сайта: Zavarka Team
Большая Энциклопедия Нефти и Газа
Геометрическая сумма
Геометрическая сумма активного и реактивного сопротивлений называется полным сопротивлением. [2]
Геометрическая сумма 2 dFnoK 0, так как на двух симметрично расположенных элементарных площадках элементарные силы трения покоя равны по величине и противоположны по направлению. [3]
Геометрическая сумма всех сил данной пространственной системы называется главным вектором. [4]
Геометрическая сумма этих трех построенных векторов, согласно ур-нию ( II. [5]
Геометрическая сумма этих компонент с течением времени описывает эллипс, частными случаями которого являются окружность и прямая линия. [6]
Геометрическая сумма любых двух компонент дает эллипс в плоскости, проходящей через эти компоненты. [7]
Геометрическая сумма двух показаний, поделенная пополам, дает точное положение плоскости. При установке уровня с помощью столбиков и призмы необходимо предварительно проверить столбики по высоте, а призму повернуть на 180 и вторично произвести два замера. [8]
Геометрическая сумма и результирующие моменты системы векторов, расположенных произвольно. [9]
Геометрическая сумма этих векторов образует, как уже отмечалось, вектор П %, амплитуда которого в установившемся режиме также является величиной постоянной. [10]
Геометрическая сумма всех трех векторов равна напряжению U на входе цепи. [11]
Геометрическая сумма ( главный вектор) всех, внутренних сил системы равняется нулю. В самом деле, по третьему закону динамики любые две точки системы ( рис. 274) действуют друг на друга с равными по модулю и противоположно направленными силами / и и / ji, сумма которых равна нулю. [12]
Геометрическая сумма всех сил данной пространственной системы называется главным вектором. [13]
Геометрическая сумма всех сил данной системы называется главным вектором этой системы. [14]
Геометрическая сумма не изменяется от перемены мест слагаемых. [15]
Геометрическая прогрессия и сумма ее членов
теория по математике 📈 последовательности
Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему, умноженному на одно и то же число.
Другими словами, последовательность (bn) – геометрическая последовательность, если для натурального n выполняются условия:
где q некоторое число, которое называется знаменатель прогрессии, и bn≠0
Формула n-ого члена геометрической прогрессии
Рассмотри на примерах применение формулы b n = b 1 q n − 1 для указанного члена геометрической прогрессии.
Пример №1. Найти четвертый член геометрической прогрессии, если известно, что b1=6, q=3. Составляем формулу для b4:
b 4 = b 1 q 4 − 1 = b 1 q 3
b 6 = b 1 q 6 − 1 = b 1 q 5 = 2 × ( − 3 ) 5 = − 486
Свойство геометрической прогрессии
Квадрат любого члена геометрической прогрессии, начиная со второго, равен произведению предыдущего и последующего ее членов. Формула:
b 2 n = b n − 1 × b n + 1
Верным является и утверждение, обратное данному: если в последовательности чисел, отличных от нуля, квадрат каждого члена, начиная со второго, равен произведению предыдущего и последующего членов, то эта последовательность чисел является геометрической прогрессией.
Другими словами, с помощью данной формулы можно найти неизвестный член геометрической прогрессии, соседние члены которого известны. Рассмотрим применение данного свойства на примерах.
Пример №2. Найти b5, если задана геометрическая прогрессия, в которой b4=32, b6=128. Составляем формулу, подставляем в нее значения и вычисляем:
b 2 5 = b 5 − 1 × b 5 + 1 = b 4 × b 6 = 32 × 128 = 4096
Этим действием мы нашли квадрат пятого члена геометрической прогрессии, поэтому извлекаем квадратный корень из числа 4096 для нахождения значения b5: b5= √ 4096 =64
Найти у, если дана геометрическая прогрессия …..24; у; 96. Видим, что у находится между соседними известными числами 24 и 96. Поэтому, следуя свойству, умножаем данные числа и извлекаем квадратный корень из полученного числа: у= √ 24 × 96 = √ 2304 =48.
Формула суммы n первых членов геометрической прогрессии
Для нахождения суммы по данной формуле нужно знать первый и последний член геометрической прогрессии, а также ее знаменатель.
Также есть вторая формула, по которой можно находить сумму нескольких первых членов прогрессии, зная только первый ее член и знаменатель: Формула суммы членов геометрической прогрессии с известным первым членом и знаменателем
Рассмотрим применение данных формул на примере, решив его двумя способами. Пример №3. Найти сумму пяти первых членов геометрической прогрессии, если известно, что b1=2; b5=162; q=-3. Способ №1 (первая формула). Составим формулу для нахождения S5:
Подставим значения b1=2; b5=162 и найдем результат:
Способ №2 (вторая формула).
Для решения нам нужен первый член и знаменатель: b1=2; q=-3. Составим формулу:
Подставим в формулу данные значения и вычислим сумму:
Таким образом, мы увидели, что у нас получился один и тот же результат 122 в обоих способах решения. Выбор формулы зависит от данных в условии задачи.