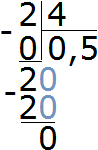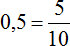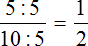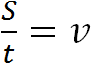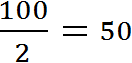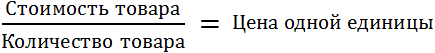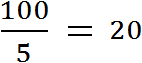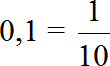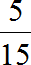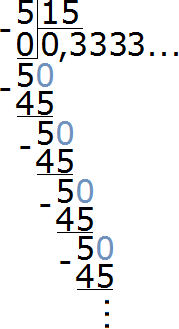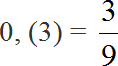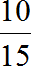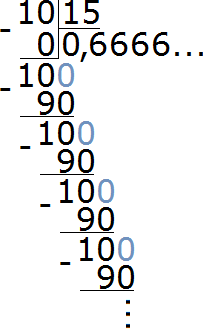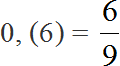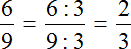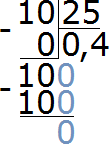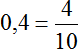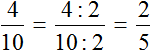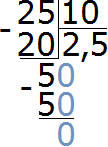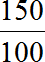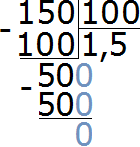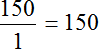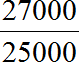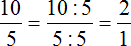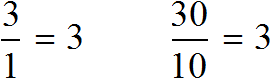что значит как соотносятся понятия

Значение слова «соотношение»

Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека

Проще говоря, соотношение показывает для каждого количества чего-то одного сколько есть чего-то другого. Например, предположим, что у кого-то есть 8 апельсинов и 6 лимонов в вазе для фруктов, соотношение апельсинов и лимонов составит 4:3 (что эквивалентно 8:6), а соотношение лимонов и апельсинов составит 3:4. Кроме того, количество апельсинов относительно общего количества фруктов составит 4:7 (что эквивалентно 8:14). Соотношение 4:7 можно преобразовать в дробь 4/7, показывающую, какую долю от общего числа фруктов составляют апельсины.

СООТНОШЕ’НИЕ, я, ср. (книжн.). Взаимное отношение, связь между двумя или несколькими предметами или явлениями. Экономика и политика находятся в постоянном соотношении. С. спроса и предложения. С. борющихся сил.

Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека

соотноше́ние

1. взаимное отношение; взаимная связь, зависимость ◆ Для меня достижимость желаемого (вещи ли, души ли) в обратном соотношении с желанностью его: чем желанней ― тем недостижимей. М. И. Цветаева, «Смерть Стаховича», 1919 г. (цитата из НКРЯ)

2. научн. мера относительной величины двух количеств ◆ В результате несколько снижается динамический диапазон сигнала, то есть соотношение самого высокого и самого низкого уровней, и плохо воспроизводятся крутые фронты. В. Хорт, «Информохранилища», 2008 г. // «Наука и жизнь» (цитата из НКРЯ) ◆ С гололёдом на улицах столицы много лет боролись, используя смесь песка и технической соли (обычное соотношение 92: 8). Александр Попов, «Ледниковый период», 2004 г. // «За рулем» (цитата из НКРЯ) ◆ Естественно, мы напрямую зависим от стабильности этой валюты, и вы прекрасно понимаете: соотношение, или курс, рубля к доллару ― это очень важно. Александр Гимельштейн, «Мы должны быть ответственны!», 2003 г. // «Восточно-Сибирская правда» (цитата из НКРЯ) ◆ Соотношение времени экспонирования ― 1: 2: 4: 8. Лев Быстров, «Цветное тоноразделение», 1974 г. // «Техника — молодежи» (цитата из НКРЯ) ◆ А оптимальное соотношение газов для роста водородных бактерий: 7 частей водорода, 2 части кислорода и 1 часть углекислого газа. Владимир Котелев, ««Водородный» белок — соперник «нефтяного»», 1974 г. // «Техника — молодежи» (цитата из НКРЯ)

Делаем Карту слов лучше вместе

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Я стал чуточку лучше понимать мир эмоций.

Вопрос: очный — это что-то нейтральное, положительное или отрицательное?

Источник

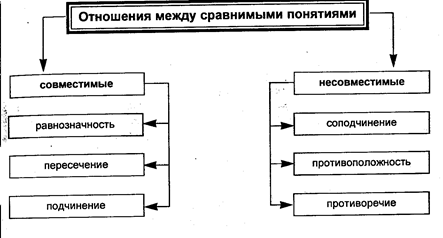
Логические отношения между понятиями

Так как все предметы находятся во взаимодействии и взаимообусловленности, то и понятия, отражающие данные предметы, также находятся в определённых отношениях. Конкретные виды отношений устанавливаются в зависимости от содержания и объёма понятий.

По содержанию могут быть два вида отношений между понятиями – сравнимость и несравнимость.

1). Сравнимыми называются понятия, отражающие некоторые общие суще­ственные признаки предмета или класса однородных предметов. Например, «право», «политика», «мораль» (общественное явление), «юрист» и «адвокат» (высшее юридическое образование), «взятка» и «кража» (правонарушения). Степень сравнимости понятий может быть различной, а сами сравнения – весьма разнообразными, отражающими всё многообразие отношений предметов и явлений в окружающем мире.

2). Несравнимыепонятия не имеют общих признаков, далеки друг от друга по свое­му содержанию. Например, «симфониче­ская музыка» и «кассационная жалоба», «процессуальные акты предварительного расследования» и «общая тетрадь», «государство» и «всемирное тяготение».

В логических отношениях могут находиться только сравнимые понятия. Логический анализ несравнимых понятий невозможен.

В зависимости от того, как соотносятся объёмы сравнимых понятий, понятия делятся на две группы: совместимые и несовместимые.

Совместимые– это такие понятия, объёмы которых совпадают полностью или частично.Несовместимые – это понятия, объёмы которых не сов­падают ни в одном элементе, но которые могут быть включены частично или полностью в объём общего для них понятия. Отношения между понятиями разделяются на отношения совместимости и несовместимости.

Отношения между понятиями принято иллюстрировать при помощи кругов Эйлера (круговых схем), названных так в честь Леонарда Эйлера (1707 – 1783) – одного из крупнейших математиков XVIII века, родившегося в Швейцарии, но весь свой талант отдавшего России. Каждый круг обозна­чает объём понятия, а любая точка внутри круга – предмет, входящий в его объём. Круговые схемы позволяют наглядно представить отношения между различными понятиями, лучше осмыслить и усвоить эти отношения.

Типы отношений совместимости понятий:

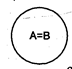
1). В отношенияхравнозначности (тождественности) находятся совместимые понятия, объёмы которых полностью совпадают. В таких понятиях мыслится один и тот же предмет или класс однородных предметов. Однако содержание этих понятий различно, так как каждое из них отражает только определённую сторону (су­щественный признак) данного предмета или класса однородных предметов.

Например, объёмы понятий А – «сын» и В – «внук» совпа­дают (каждый сын есть чей-то внук и каждый внук – чей-то сын), но содержания их различны. Аналогично: «Россия» и «Российская Федерация», «Ленинград» и «Санкт-Петербург», «равносторонний прямоугольник» и «квадрат».

Необходимо отличать равнозначные понятия от равнозначных слов-синонимов. У равнозначных понятий одинаковый объём, но разное содержание. А слова-синонимы выражают понятия с одинаковым объёмом и содержанием. Замена в любом осмысленном высказывании слов-си­нонимов друг с другом не влияет на смысл высказывания. Замена же слов, вы­ражающих равнозначные понятия, может привести к существенному искаже­нию смысла. Например, в высказывании «В 1980 году Москва была столицей игр XXII Олимпиады» нельзя заменить понятие «столица игр XXII Олимпиа­ды» равнозначным ему понятием «центр Московской области». Таким обра­зом, слова или словосочетания, выражающие равнозначные понятия, сами по себе не являются равнозначными.

2). В отношенииподчинения (субординации) находятся совместимые понятия, объём одно­го из которых полностью входит в объём другого, составляя его часть, не исчерпывая всего его содержания.

В таком отношении, например, находятся понятия А – «кража» и В – «кража личного имущества граждан», «металл» и «золото», «дерево» и «берёза».

Объём первого понятия шире объёма второго поня­тия: кроме кражи личного имущества граждан в него входит также кража государственного, кооперативного имущества; есть другие металлы, кроме золота; берёза – один из видов деревьев.

Из двух понятий, находящихся в отношении подчинения, понятие с большим объёмом (подчиняющее) является родовым, илиродом, по отношению к понятию с меньшим объёмом (подчинённому), а последнее по отношению к первому называется видовым, иливидом. Понятие «республика» является родовым по отношению к понятию «федеративная республика», но видовым по отношению к понятию «государство».

Предельно общие понятия являются только родовыми, единичные понятия – только видовыми, остальные могут быть и теми, и другими. Родовидовые отношения лежат в основе логических операций ограничения и обобщения понятий, деления объёма понятий и некоторых видов определения.

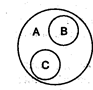
3). В отношениипересечения (перекрещивания) находятся совместимые поня­тия, у которых объёмы частично совпадают. Частично совпадает и содержание данных понятий.

Например, пересекающимися понятиями являются А – «спортсмен» и В – «студент»: часть спортсменов являются студентами, a часть студентов – спортсменами. В совместившейся части кругов мыслятся те спортсмены, которые являются студентами, а также те студенты, которые являются спортсменами.

При иллюстрации отношений междунесовместимыми понятиями возни­кает потребность во введении более широкого по объёму понятия, которое включало бы объёмы несовместимых понятий.

Типы отношений несовместимости понятий:

1). В отношении соподчинения (координации) находятся два или более непересекающихся понятий, принадлежащих общему родо­вому понятию.

Соподчинённые понятия В и С – это виды одного рода А, у них общий родовой признак, но видовые признаки различны. Например, В – «должностное преступление» и С – «хозяйствен­ное преступление», где А – «преступление»; «монархия» и «республика» – соподчинённые понятия при родовом понятии «форма правления».

2). В отношениипротивоположности (контрарности) находятся понятия, которые являются видами одного и того же рода, и при этом содержат взаимоисключающие при­знаки.

Например, А – «тяжкое телесное повреждение» и В – «лёгкое телесное повреждение», где родовое понятие – «телесное повреждение». Объёмы противоположных понятий составляют лишь часть объёма общего для них родо­вого понятия: «богатство» и «бедность», «мудрость» и «глупость», «добро» и «зло», «чёрный» и «белый».

Слова, выражающие противоположные понятия, называютсяантонимами. Например: осудить – оправдать, обвинение – защита, алиби – улики, мягкое наказание – строгое наказание и др. Неудачное использование анто­нимов приводит к неясности мысли: «Потерпевший делал всё возможное, силясь побороть свою слабость» или «Гудов участвовал в преступных действиях в силу слабости своего характера».

3). В отношениипротиворечия (контрадикторности) находятся такие два поня­тия, которые являются видами одного и того же рода, и при этом одно понятие указывает на некоторые признаки, а другое эти признаки отрицает, исключает, не заменяя их никакими другими признаками.

Например, А – «виновный» и не-А – «невиновный», где родовое понятие – «человек». Объёмы двух противоречащих понятий со­ставляют весь объём рода, видами которого они являются (закон «третьего не дано»): «металл» – «неметалл», «живое» – «неживое».

Итак, в логике выделяется шесть вариантов отношений между понятиями. Любые два сравнимых понятия обязательно находятся в одном из шести указанных случаев отношений.

Надо обратить внимание на то, что если два понятия обозначают часть и целое, например, «месяц»и «год»,то они находятся в отношении соподчинения, хотя может показаться, что между ними отношение подчинения, ведь месяц входит в год. Однако если бы понятия «месяц»и «год» были подчинёнными, то тогда надо было бы утверждать, что месяц – это обязательно год, а год – это не обязательно месяц. Месяц – это не год, а год – это не месяц, но и то, и другое – отрезок времени, следовательно, понятия «месяц»и «год»,так же как и понятия «книга» и «страница книги», «автомобиль» и «колесо автомобиля», «молекула» и «атом»и т. п., находятся в отношении соподчинения, так как часть и целое – не то же самое, что вид и род.

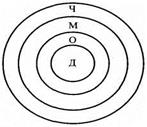
Рассмотрим отношения между понятиями «дедушка», «отец», «мужчина», «человек»с помощью круговой схемы.

Как видим, указанные четыре понятия находятся в отношении последовательного подчинения: дедушка – это обязательно отец, а отец – не обязательно дедушка; любой отец – это обязательно мужчина, однако не всякий мужчина является отцом; и, наконец, мужчина – это обязательно человек, но человеком может быть не только мужчина.

Отношения между понятиями «хищник», «рыба», «акула», «пиранья», «щука»изображаются следующей схемой:

Подытоживая всё сказанное, отметим, что отношения между понятиями – этоотношения между их объёмами.Значит, для того чтобы было возможно установить отношения между понятиями, их объём должен быть резким, а содержание, соответственно, ясным, то есть эти понятия должны быть определёнными. Что касается неопределённых понятий, то установить точные отношения между ними достаточно сложно, фактически невозможно, ведь из-за неясности их содержания и нерезкости объёма два каких-нибудь неопределённых понятия можно будет характеризовать как равнозначные или как пересекающиеся, или как подчиняющиеся и т. д. Например, возможно ли установить отношение между неопределёнными понятиями «неаккуратность» и «небрежность»?То ли это будет равнозначность, то ли подчинение – точно сказать невозможно. Таким образом, отношения между неопределёнными понятиями являются также неопределёнными.

Знание отношений между понятиями имеет огромное значение для их правильного употребления в устной и письменной речи, отражения действительных отношений между самими вещями, обозначаемыми понятиями. Содержание равнозначных понятий может меняться (от негативной оценки к нейтральной или положительной, и наоборот). Один и тот же человек может обозначаться по-разному: фамилия (Петров), местоимение (он), социальный статус (студент), ситуация (потерпевший).

Логические ошибки в отношениях между понятиями:

1) использование неравнозначных понятий в качестве равнозначных: плебисцит (опрос общественного мнения) и референдум (опрос, имеющий юридическую силу) – одинаковы по процедуре проведения;

2) использование равнозначных понятий в качестве различных («суверенность» и «независимость», «легальность» и «законность»);

3) смешение родовых и видовых понятий, неправильное их употребление (вместо «женщина» говорится «человек») для увеличения или уменьшения выразительности речи.

Подчинённые родовидовые понятия пишутся слитно («западноевропейский», «восточнославянский»), а соподчинённые понятия – через дефис («северо-запад», «газетно-журнальный зал», «Австро-Венгрия»).

Таким образом, уяснение логической структуры понятий, определение их видов и отношений между сравнимыми понятиями даёт возможность пе­рейти к рассмотрению логических действий, или операций над понятиями.

Источник

Отношения между понятиями

Понятия делятся на

Сравнимые понятия имеют общие признаки, по ко­торым их можно сравнить и отнести в связи с этим к определенному классу предметов. Например, можно сравнить муху и самолет? Можно, поскольку и первому, и второму понятию присущ признак «летать». Понятия «студент» и «аспирант» относятся к общему родовому понятию «учащийся», поэтому также являются сравнимыми и т. п.

Сравнимые понятия, в свою очередь, делятся на совместимые и несо­вместимые.

Несравнимые понятия не имеют общих признаков. Нельзя, например, сравнить такие понятия, как «канцелярский прибор» и «галактика», у них от­сутствует общее основание для их сравнения.

Совместимыми называются понятия, объемы которых имеют общие элементы; объемы несовместимых понятий не имеют общих элементов.

Отношения между объемами понятий принято изображать с помощью круговых диаграмм (кругов) Эйлера, которые схематично изображают объемы понятий, отношения между которыми необходимо установить. При этом мыс­лится, что внутри изображенных нами кругов находятся все предметы, носящие имя понятий, отношение между объемами которых устанавливается.

Виды совместимости понятий

1) Тождество (равнообъемность, равнозначность)

В отношении тождества находятся такие понятия, объемы которых полностью совпадают.

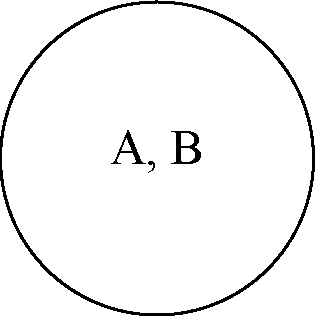
Москва (А), Столица России (В);

Преступление (А), Общественно опасное деяние (В).

2) Пересечение

В отношении пересечения находятся понятия, объемы которых частич­но совпадают.

Не каждый преподаватель является женщиной. Так же как и не каждая женщина является препо­давателем, но есть такие преподаватели, которые одновременно являются женщинами.

3) Подчинение

В отношении подчинения находятся такие понятия, объем одного из ко­торых полностью входит в объем другого, но не исчерпывает его.

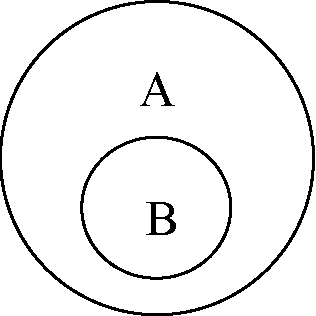
При этом понятие с большим объемом (ро­довое) называется подчиняющим (А), понятие с меньшим объемом (видовое) – подчиненным (В).

Преступление (А), Кража (В).

Виды несовместимости понятий

1) Соподчинение

2) Противоположность

3) Противоречие

Виновный (А) Невиновный (не-А)

Для чего необходимо уметь правильно соотносить объемы понятий?

Имея представление о соотношении понятий, человек верно строит с ни­ми суждения.

Например, как соотносятся между собой понятия «преступник» и «нар­коман»? Отношение пересечения, но никак не подчинение. Отсюда следует, что суждение «Все наркоманы преступники» – ложно.

Категории

Нормативные правовые акты в Российской Федерации

Постановление Пленума Верховного Суда Российской Федерации от 25 декабря 2018 года № 50 «О практике рассмотрения судами дел об оспаривании нормативных правовых актов и актов, содержащих разъяснения законодательства и обладающих нормативными свойствами»

Постановление Пленума Верховного Суда Российской Федерации от 25 декабря 2018 года № 49 «О некоторых вопросах применения общих положений Гражданского кодекса Российской Федерации о заключении и толковании договора»

Постановление Пленума Верховного Суда Российской Федерации от 25 декабря 2018 года № 48 «О некоторых вопросах, связанных с особенностями формирования и распределения конкурсной массы в делах о банкротстве граждан»

Постановление Пленума Верховного Суда Российской Федерации от 25 декабря 2018 года № 46 «О некоторых вопросах судебной практики по делам о преступлениях против конституционных прав и свобод человека и гражданина (статьи 137, 138, 138.1, 139, 144.1, 145, 145.1 Уголовного кодекса Российской Федерации)»

Постановление Пленума ВС РФ от 29 ноября 2018 года № 41 «О судебной практике по уголовным делам о нарушениях требований охраны труда, правил безопасности при ведении строительных или иных работ либо требований промышленной безопасности опасных производственных объектов»

Согласно Федеральному закону от 28.11.2018 N 451-ФЗ «О внесении изменений в отдельные законодательные акты Российской Федерации» пересмотрен порядок разрешения гражданских и административных дел в судах (со дня начала деятельности кассационных судов общей юрисдикции и апелляционных судов общей юрисдикции, но не позднее 1 октября 2019 года).

Источник

Соотношения

Соотношением называют некоторую взаимосвязь между сущностями нашего мира. Это могут быть числа, физические величины, предметы, продукты, явления, действия и даже люди.

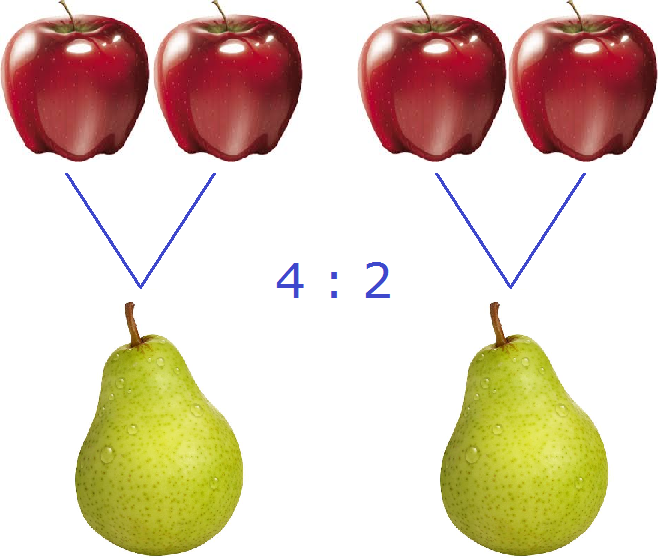
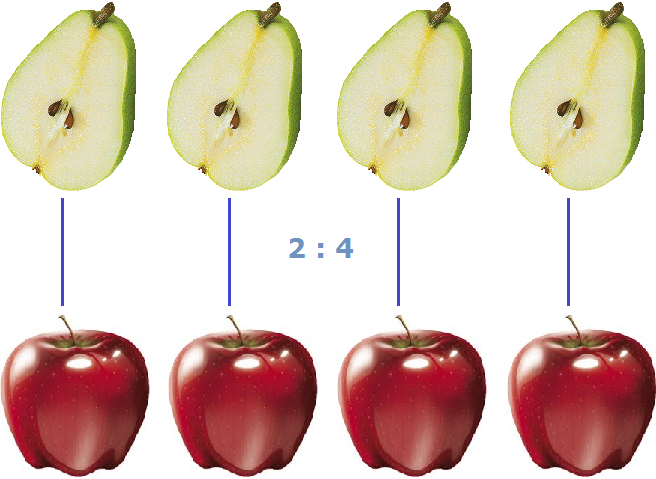
В повседневной жизни, когда речь заходит о соотношениях, мы говорим «соотношения того-то и того-то». Например, если в вазе лежит 4 яблока и 2 груши, то мы говорим «соотношения яблок и груш» или если поменять местами яблоки и груши, то «соотношения груш и яблок».

В математике соотношение чаще употребляется как «отношение того-то к тому-то». Например, соотношение четырёх яблок и двух груш, которые мы рассматривали выше, в математике будет читаться как «отношение четырех яблок к двум грушам» или если поменять местами яблоки и груши, то «отношение двух груш к четырем яблокам».

Запишем соотношение четырех яблок и двух груш с помощью символа соотношения:

Это соотношение можно прочитать как «четыре к двум» либо «соотношение четырех яблок и двух груш» либо «четыре яблока относится к двум грушам»

В дальнейшем соотношение мы будем называть просто отношением.

Что такое отношение?

Отношением в математике называют частное двух чисел.

Данное отношение представляет собой деление числа 4 на число 2. Если выполнить это деление, мы получим ответ на вопрос сколько яблок приходится на единицу груши

Получили 2. Значит четыре яблока и две груши (4 : 2) соотносятся (взаимосвязаны друг с другом) так, что на одну грушу приходится два яблока

На рисунке показано, как четыре яблока и две груши соотносятся между собой. Видно, что на каждую грушу приходятся два яблока.

Чтобы найти значение дроби нужно вспомнить, как делить меньшее число на большее

Получили 0,5. Переведём эту десятичную дробь в обыкновенную:

Сократим полученную обыкновенную дробь на 5

Получили ответ (половину груши). Значит две груши и четыре яблока (2 : 4) соотносятся (взаимосвязаны друг с другом) так, что на одно яблоко приходится половина груши

На рисунке показано, как две груши и четыре яблока соотносятся между собой. Видно, что на каждое яблоко приходится половинка груши.

Числа, из которых составлено отношение, называют членами отношения. Например, в отношении 4 : 2 членами являются числа 4 и 2.

Рассмотрим другие примеры соотношений. Для приготовления чего-либо составляется рецепт. Рецепт строят из соотношений между продуктами. Например, для приготовления овсяной каши обычно требуется стакан хлопьев на два стакана молока или воды. Получается соотношение 1 : 2 («один к двум» или «один стакан хлопьев на два стакана молока»).

Если перевернуть соотношение 1 : 2 то получится соотношение 2 : 1 («два к одному» или «два стакана молока на один стакан хлопьев»). Преобразуем соотношение 2 : 1 в дробь, получим . Вычислив эту дробь, получим 2. Значит два стакана молока и один стакан хлопьев соотносятся (взаимосвязаны друг с другом) так, что на один стакан хлопьев приходятся два стакана молока.

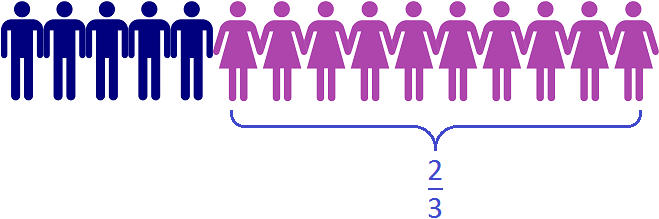
Пример 2. В классе 15 школьников. Из них 5 – это мальчики, 10 – девочки. Можно записать соотношение девочек и мальчиков 10 : 5 и преобразовать это соотношение в дробь . Вычислив эту дробь получим 2. То есть девочки и мальчики соотносятся между собой так, что на каждого мальчика приходятся две девочки

На рисунке показано, как десять девочек и пять мальчиков соотносятся между собой. Видно, что на каждого мальчика приходятся две девочки.

Соотношение не всегда можно обращать в дробь и находить частное. В некоторых случаях это будет нелогично.

Так, если перевернуть отношение получится , а это уже отношение мальчиков к девочкам. Если вычислить эту дробь получается 0,5. Получается, что пять мальчиков относятся к десяти девочкам так, что на каждую девочку приходится половина мальчика. Математически это конечно верно, но с точки зрения реальности не совсем разумно, ибо мальчик это живой человек и его нельзя просто так взять и разделить, как грушу или яблоко.

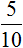
Умение построить правильное отношение — важный навык при решении задач. Так в физике, отношение пройденного расстояния ко времени есть скорость движения.

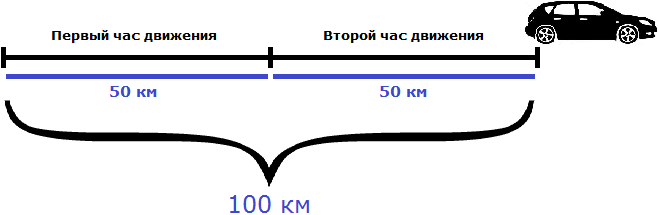
Предположим, что автомобиль проехал 100 километров за 2 часа. Тогда отношение пройденных ста километров к двум часам будет скоростью движения автомобиля:

Скоростью принято называть расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда. А отношение, как было сказано ранее, позволяет узнать сколько количества одной сущности приходится на единицу другой. В нашем примере отношение ста километров к двум часам показывает сколько километров приходится на один час движения. Видим, что на каждый час движения приходятся 50 километров

Пример 2. Отношение стоимости товара к его количеству есть цена одной единицы товара

Если мы взяли в магазине 5 шоколадных батончиков и их общая стоимость составила 100 рублей, то мы можем определить цену одного батончика. Для этого нужно найти отношение ста рублей к количеству батончиков. Тогда получим, что на один батончик приходятся 20 рублей

Сравнение величин

Ранее мы узнали, что отношение между величинами разной природы образуют новую величину. Так, отношение пройденного расстояния ко времени есть скорость движения. Отношение стоимости товара к его количеству есть цена одной единицы товара.

Но отношение можно использовать и для сравнения величин. Результат выполнения такого отношения есть число, показывающее во сколько раз первая величина больше второй или какую часть первая величина составляет от второй.

Чтобы узнать во сколько раз первая величина больше второй, в числитель отношения нужно записать большую величину, а в знаменатель меньшую величину.

Чтобы узнать какую часть первая величина составляет от второй, в числитель отношения нужно записать меньшую величину, а в знаменатель большую величину.

Рассмотрим числа 20 и 2. Давайте узнаем во сколько раз число 20 больше числа 2. Для этого находим отношение числа 20 к числу 2. В числителе отношения записываем число 20, а в знаменателе — число 2

Значение данного отношения равно десяти

Отношение числа 20 к числу 2 есть число 10. Это число показывает во сколько раз число 20 больше числа 2. Значит число 20 больше числа 2 в десять раз.

Пример 2. В классе 15 школьников. 5 из них это мальчики, 10 – девочки. Определить во сколько раз девочек больше мальчиков.

Записываем отношение девочек к мальчикам. В числителе отношения записываем количество девочек, в знаменатель отношения — количество мальчиков:

Значение данного отношения равно 2. Значит в классе из 15 человек девочек в два раза больше мальчиков.

Здесь уже не стоит вопрос о том, сколько девочек приходятся на одного мальчика. В данном случае отношение используется для сравнения количества девочек с количеством мальчиков.

Пример 3. Какую часть число 2 составляет от числа 20.

Находим отношение числа 2 к числу 20. В числителе отношения записываем число 2, а в знаменателе — число 20

Чтобы найти значение данного отношения, нужно вспомнить, как делить меньшее число на большее

Значение отношения числа 2 к числу 20 есть число 0,1

В данном случае десятичную дробь 0,1 можно перевести в обыкновенную. Такой ответ будет проще для восприятия:

Значит число 2 от числа 20 составляет одну десятую часть.

Можно сделать проверку. Для этого найдём от числа 20. Если мы всё сделали правильно, то должны получить число 2

Получили число 2. Значит одна десятая часть от числа 20 есть число 2. Отсюда делаем вывод, что задача решена верно.

Пример 4. В классе 15 человек. 5 из них это мальчики, 10 – девочки. Определить какую часть от общего количества школьников составляют мальчики.

Записываем отношение мальчиков к общему количеству школьников. В числителе отношения записываем пять мальчиков, в знаменателе — общее количество школьников. Общее количество школьников это 5 мальчиков плюс 10 девочек, поэтому в знаменателе отношения записываем число 15

Чтобы найти значение данного отношения, нужно вспомнить, как делить меньшее число на большее. В данном случае число 5 нужно разделить на число 15

При делении 5 на 15 получается периодическая дробь. Переведём эту дробь в обыкновенную

Сократим полученную дробь на 3

Получили окончательный ответ . Значит мальчики составляют одну треть от всего класса

На рисунке видно, что в классе из 15 школьников треть класса составляют 5 мальчиков.

Если для проверки найти от 15 школьников, то мы получим 5 мальчиков

Записываем отношение числа 35 к числу 5. В числитель отношения нужно записать число 35, в знаменатель — число 5, но не наоборот

Значение данного отношения равно 7. Значит число 35 в семь раз больше числа 5.

Пример 6. В классе 15 человек. 5 из них это мальчики, 10 – девочки. Определить какую часть от общего количества составляют девочки.

Записываем отношение девочек к общему количеству школьников. В числителе отношения записываем десять девочек, в знаменателе — общее количество школьников. Общее количество школьников это 5 мальчиков плюс 10 девочек, поэтому в знаменателе отношения записываем число 15

Чтобы найти значение данного отношения, нужно вспомнить, как делить меньшее число на большее. В данном случае, число 10 нужно разделить на число 15

При делении 10 на 15 получается периодическая дробь. Переведём эту дробь в обыкновенную

Сократим полученную дробь на 3

На рисунке видно, что в классе из 15 школьников две трети класса составляют 10 девочек.

Если для проверки найти от 15 школьников, то получим 10 девочек

Пример 7. Какую часть 10 см составляют от 25 см

Записываем отношение десяти сантиметров к двадцати пяти сантиметрам. В числителе отношения записываем 10 см, в знаменателе — 25 см

Чтобы найти значение данного отношения, нужно вспомнить, как делить меньшее число на большее. В данном случае число 10 нужно разделить на число 25

Переведём полученную десятичную дробь в обыкновенную

Сократим полученную дробь на 2

Получили окончательный ответ . Значит 10 см составляют от 25 см.

Пример 8. Во сколько раз 25 см больше 10 см

Записываем отношение двадцати пяти сантиметров к десяти сантиметрам. В числителе отношения записываем 25 см, в знаменателе — 10 см

Найдём значение данного отношения

Получили ответ 2,5. Значит 25 см больше 10 см в 2,5 раза (в два с половиной раза)

Важное замечание. При нахождении отношения одноименных физических величин эти величины обязательно должны быть выражены в одной единице измерения, в противном случае ответ будет неверным.

Например, если мы имеем дело с двумя длинами и хотим узнать во сколько раз первая длина больше второй или какую часть первая длина составляет от второй, то обе длины сначала нужно выразить в одной единице измерения.

Пример 9. Во сколько раз 150 см больше 1 метра?

Сначала сделаем так, чтобы обе длины были выражены в одной единице измерения. Для этого переведем 1 метр в сантиметры. Один метр это сто сантиметров

1 м = 100 см

Теперь находим отношение ста пятидесяти сантиметров к ста сантиметрам. В числителе отношения записываем 150 сантиметров, в знаменателе — 100 сантиметров

Найдём значение данного отношения

Получили ответ 1,5. Значит 150 см больше 100 см в 1,5 раза (в полтора раза).

А если бы не стали переводить метры в сантиметры и сразу попытались найти отношение 150 см к одному метру, то у нас получилось бы следующее:

Получилось бы, что 150 см больше одного метра в сто пятьдесят раз, а это неверно. Поэтому обязательно нужно обращать внимание на единицы измерения физических величин, которые участвуют в отношении. Если эти величины выражены в разных единицах измерения, то для нахождения отношения этих величин, нужно перейти к одной единице измерения.

Пример 10. В прошлом месяце зарплата человека составляла 25000 рублей, а в текущем месяце зарплата выросла до 27000 рублей. Определить во сколько раз выросла зарплата

Записываем отношение двадцати семи тысяч к двадцати пяти тысячам. В числителе отношения записываем 27000, в знаменателе — 25000

Найдём значение данного отношения

Получили ответ 1,08. Значит зарплата выросла в 1,08 раза. В будущем, когда мы познакомимся с процентами, такие показатели как зарплата будем выражать в процентах.

Пример 11. Ширина многоквартирного дома 80 метров, а высота 16 метров. Во сколько раз ширина дома больше его высоты?

Записываем отношение ширины дома к его высоте:

Значение данного отношения равно 5. Значит ширина дома в пять раз больше его высоты.

Свойство отношения

Отношение не изменится если его члены умножить или разделить на одно и тоже число.

Это одно из важнейших свойств отношения следует из свойства частного. Мы знаем, что если делимое и делитель умножить или разделить на одно и то же число, то частное не изменится. А поскольку отношение является ничем иным как делением, то свойство частного работает и для него.

В нашем примере удобнее разделить члены отношения на их наибольший общий делитель (НОД).

НОД членов 10 и 5 это число 5. Поэтому можно разделить члены отношения на число 5

Получили новое отношение . Это есть отношение два к одному (2:1). Данное отношение, как и прошлое отношение 10:5 показывает, что на одного мальчика приходятся две девочки.

На рисунке показано отношение 2 : 1 (два к одному). Как и в прошлом отношении 10 : 5 на одного мальчика приходятся две девочки. Другими словами, отношение не изменилось.

Пример 2. В одном классе 10 девочек и 5 мальчиков. В другом классе 20 девочек и 10 мальчиков. Во сколько раз в первом классе девочек больше мальчиков? Во сколько раз во втором классе девочек больше мальчиков?

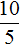
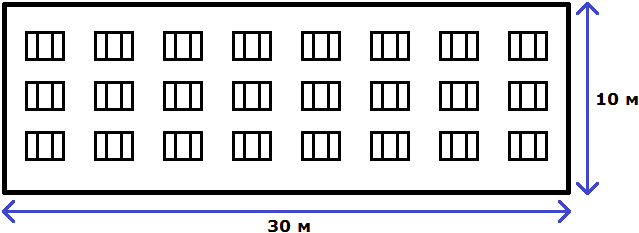
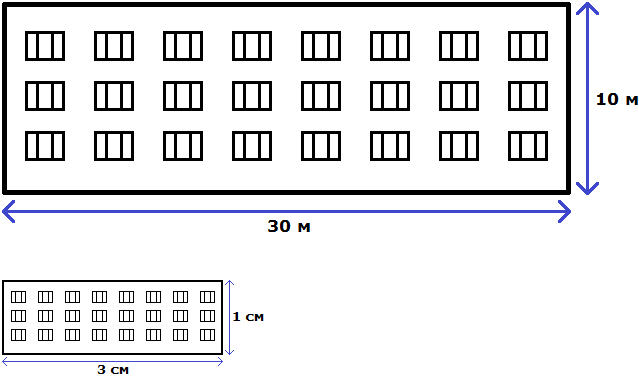
В обоих классах девочек в два раза больше мальчиков, поскольку отношения и равны одному и тому же числу.

Свойство отношения позволяет строить различные модели, которые имеют схожие параметры с реальным объектом. Предположим, что многоквартирный дом имеет ширину 30 метров и высоту 10 метров.

Переведем метры в сантиметры. 3 метра это 300 сантиметров, а 1 метр это 100 сантиметров

3 м = 300 см

1 м = 100 см

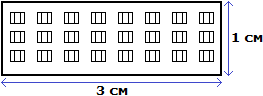
Имеем отношение 300 см : 100 см. Разделим члены этого отношения на 100. Получим отношение 3 см : 1 см. Теперь можно нарисовать дом с шириной 3 см и высотой 1 см

Конечно нарисованный дом намного меньше реального дома, но неизменным осталось отношение ширины и высоты. Это позволило нам нарисовать дом, максимально похожий на реальный

Отношение можно понимать и другим образом. Изначально было сказано, что у реального дома ширина составляет 30 метров, а высота 10 метров. Итого получается 30+10, то есть 40 метров.

Эти 40 метров можно понимать, как 40 частей. Отношение 30 : 10 говорит о том, что 30 частей приходится на ширину, а 10 частей на высоту.

Далее члены отношения 30 : 10 были разделены на 10. В результате получилось отношение 3 : 1. Это отношение можно понимать, как 4 части, три из которых приходится на ширину, одна — на высоту. В этом случае обычно требуется узнать сколько конкретно метров приходится на ширину и высоту.

Другими словами, нужно узнать сколько метров приходится на 3 части и сколько метров приходится на 1 часть. Сначала надо узнать сколько метров приходится на одну часть. Для этого общие 40 метров нужно разделить на 4, поскольку в отношении 3 : 1 всего четыре части

Далее с помощью умножения определяют сколько метров приходятся на ширину и высоту. Члены, которые даны в отношении используют в качестве сомножителя.

Определим сколько метров приходится на ширину:

Определим сколько метров приходится на высоту:

Несколько членов отношения

Если в отношении дано несколько членов, то их можно понимать как части от чего-либо.

Отношение 2 : 1 : 3 говорит о том, что мама получила 2 части, папа — 1 часть, дочка — 3 части. Другими словами, каждый член отношения 2 : 1 : 3 это определенная часть от 18 яблок:

Узнаем сколько яблок приходится на одну часть. Для этого 18 яблок разделим на 6

18 : 6 = 3 (яблока на одну часть)

Узнаем сколько яблок получила мама:

Узнаем сколько яблок получил папа:

Узнаем сколько яблок получила дочка:

4 килограмма нового серебра будет содержать 3 части никеля, 4 части цинка и 13 частей меди. Сначала узнаем сколько всего частей будет в четырех килограммах серебра:

3 + 4 + 13 = 20 (частей)

Определим сколько килограммов будет приходиться на одну часть:

Определим сколько килограммов никеля будет содержáться в 4 кг нового серебра. В отношении 3 : 4 : 13 указано, что три части сплава содержат никель. Поэтому умножаем 0,2 на 3:

0,2 кг × 3 = 0,6 кг никеля

Теперь определим сколько килограммов цинка будет содержáться в 4 кг нового серебра. В отношении 3 : 4 : 13 указано, что четыре части сплава содержат цинк. Поэтому умножаем 0,2 на 4:

0,2 кг × 4 = 0,8 кг цинка

Теперь определим сколько килограммов меди будет содержáться в 4 кг нового серебра. В отношении 3 : 4 : 13 указано, что тринадцать частей сплава содержат медь. Поэтому умножаем 0,2 на 13:

0,2 кг × 13 = 2,6 кг меди

Значит, чтобы получить 4 кг нового серебра, нужно взять 0,6 кг никеля, 0,8 кг цинка и 2,6 кг меди.

Определим сколько граммов сплава приходится на одну часть. В условии сказано, что для изготовления куска латуни требуется 120 г меди. Также сказано, что три части сплава содержат медь. Если разделить 120 на 3, мы узнаем сколько граммов сплава приходится на одну часть:

120 : 3 = 40 граммов на одну часть

Теперь определим сколько требуется цинка для изготовления куска латуни. Для этого 40 граммов умножим на 2, поскольку в отношении 3 : 2 указано, что две части содержат цинк:

40 г × 2 = 80 граммов цинка

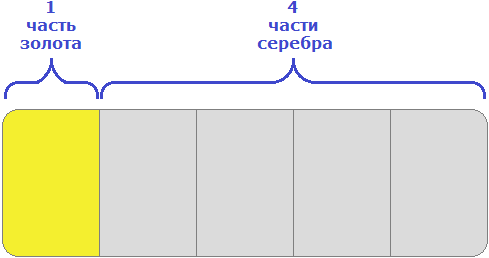
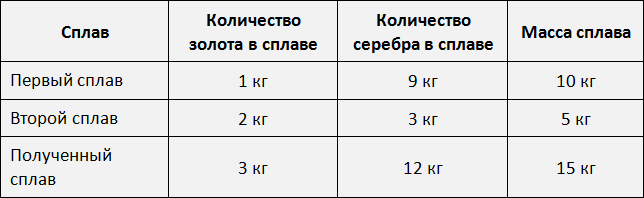
Пример 4. Взяли два сплава золота и серебра. В одном количество этих металлов находится в отношении 1 : 9, а в другом 2 : 3. Сколько нужно взять каждого сплава, чтобы получить 15 кг нового сплава, в котором золото и серебро относилось бы как 1 : 4?

Решение

15 кг нового сплава должны состоять в отношении 1 : 4. Это отношение говорит о том, что на одну часть сплава будет приходиться золото, а на четыре части будет приходиться серебро. Всего же частей пять. Схематически это можно представить следующим образом

Определим массу одной части. Для этого сначала сложим все части (1 и 4), затем массу сплава разделим на количество этих частей

1 + 4 = 5
15 кг : 5 = 3 кг

Одна часть сплава будет иметь массу 3 кг. Тогда в 15 кг нового сплава будет содержáться 3 × 1 = 3 кг золота и серебра 3 × 4 = 12 кг серебра.

Поэтому для получения сплава массой 15 кг нам нужно 3 кг золота и 12 кг серебра.

Теперь ответим на вопрос задачи — « Сколько нужно взять каждого сплава? »

Первого сплава мы возьмем 10 кг, поскольку золото и серебро в нём находятся в отношении 1 : 9. То есть этот первый сплав даст нам 1 кг золота и 9 кг серебра.

Второго сплава мы возьмем 5 кг, поскольку золото и серебро находятся в нём в отношении 2 : 3. То есть этот второй сплав даст нам 2 кг золота и 3 кг серебра.

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Источник