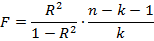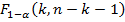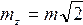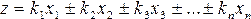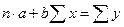что значит коэффициент аппроксимации
Метод аппроксимации в Microsoft Excel
Среди различных методов прогнозирования нельзя не выделить аппроксимацию. С её помощью можно производить приблизительные подсчеты и вычислять планируемые показатели, путем замены исходных объектов на более простые. В Экселе тоже существует возможность использования данного метода для прогнозирования и анализа. Давайте рассмотрим, как этот метод можно применить в указанной программе встроенными инструментами.
Выполнение аппроксимации
Наименование данного метода происходит от латинского слова proxima – «ближайшая» Именно приближение путем упрощения и сглаживания известных показателей, выстраивание их в тенденцию и является его основой. Но данный метод можно использовать не только для прогнозирования, но и для исследования уже имеющихся результатов. Ведь аппроксимация является, по сути, упрощением исходных данных, а упрощенный вариант исследовать легче.
Главный инструмент, с помощью которого проводится сглаживания в Excel – это построение линии тренда. Суть состоит в том, что на основе уже имеющихся показателей достраивается график функции на будущие периоды. Основное предназначение линии тренда, как не трудно догадаться, это составление прогнозов или выявление общей тенденции.
Но она может быть построена с применением одного из пяти видов аппроксимации:
Рассмотрим каждый из вариантов более подробно в отдельности.
Способ 1: линейное сглаживание
Прежде всего, давайте рассмотрим самый простой вариант аппроксимации, а именно с помощью линейной функции. На нем мы остановимся подробнее всего, так как изложим общие моменты характерные и для других способов, а именно построение графика и некоторые другие нюансы, на которых при рассмотрении последующих вариантов уже останавливаться не будем.
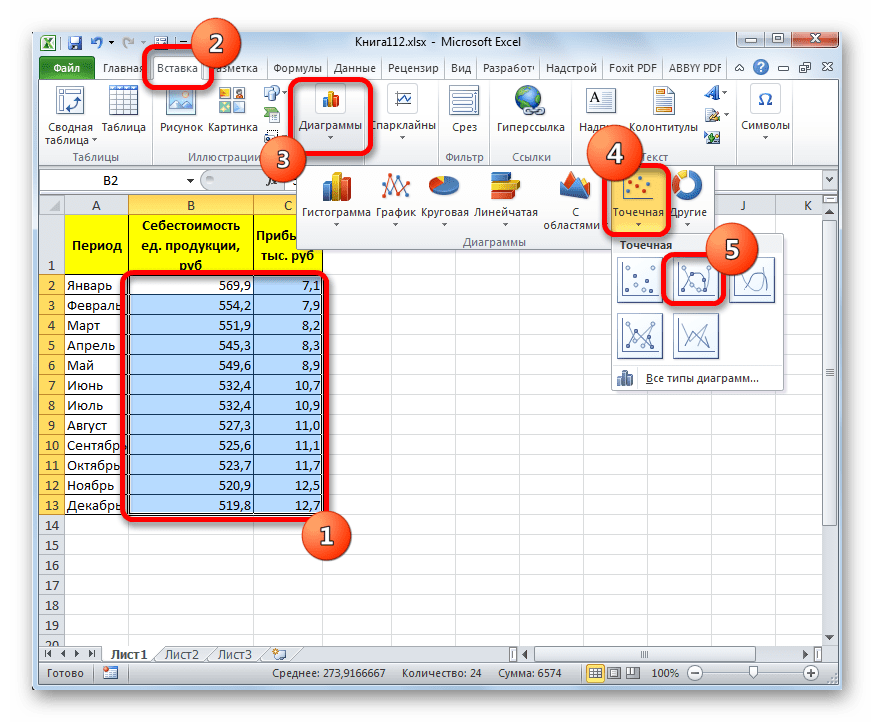
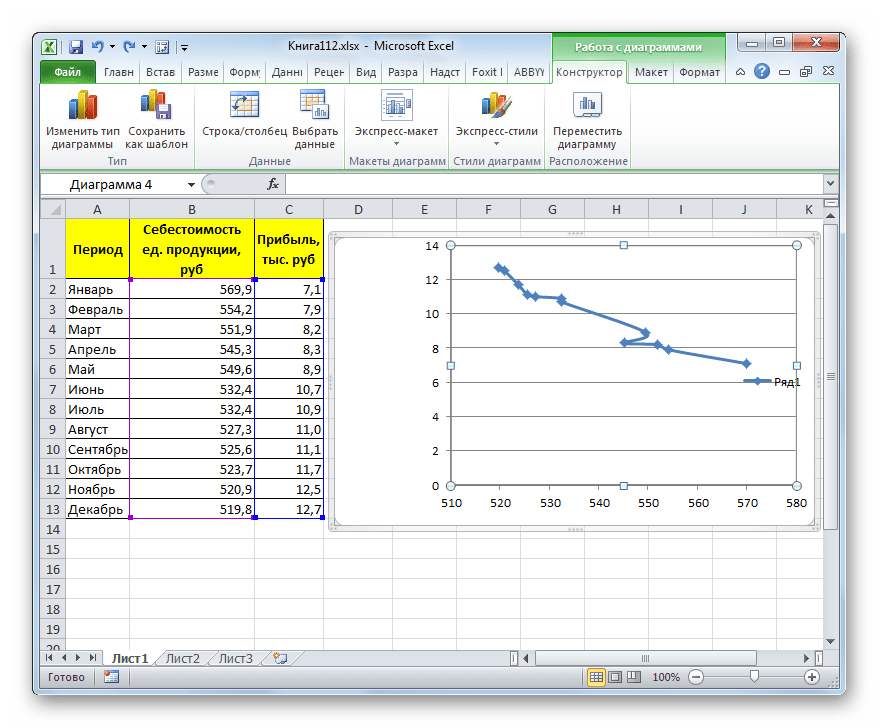
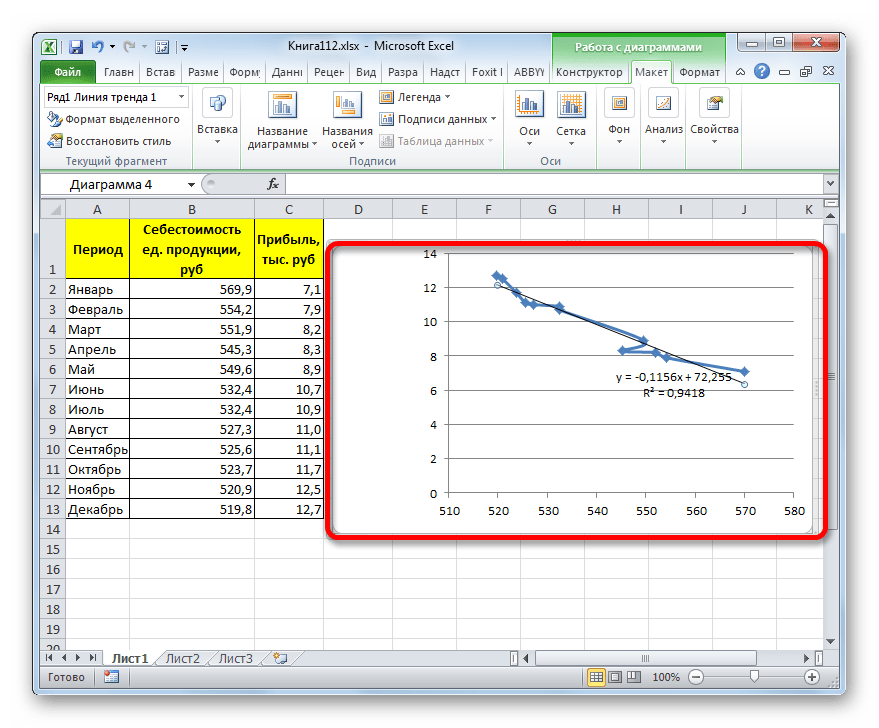
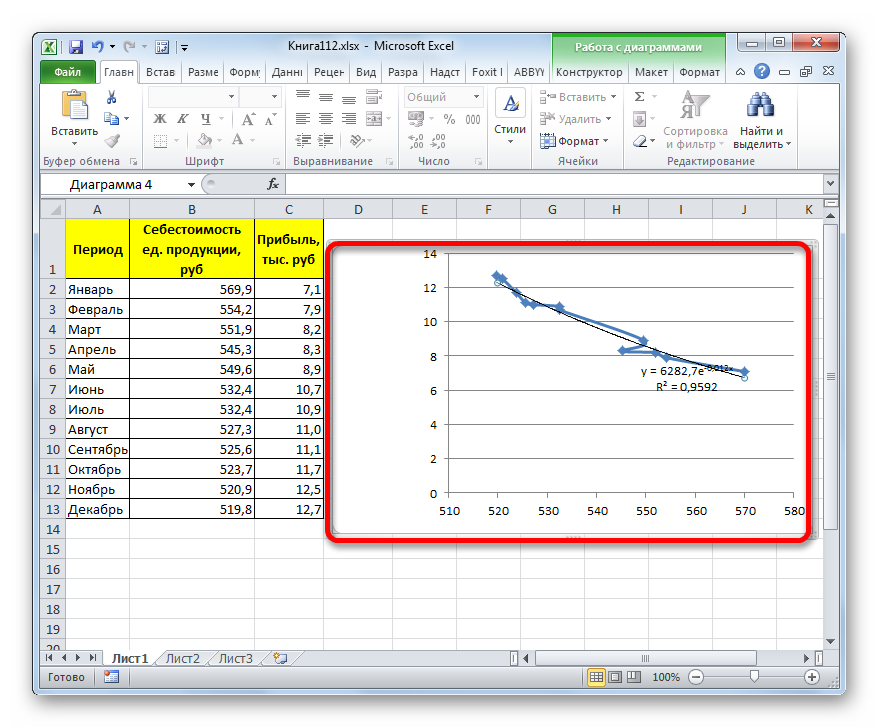
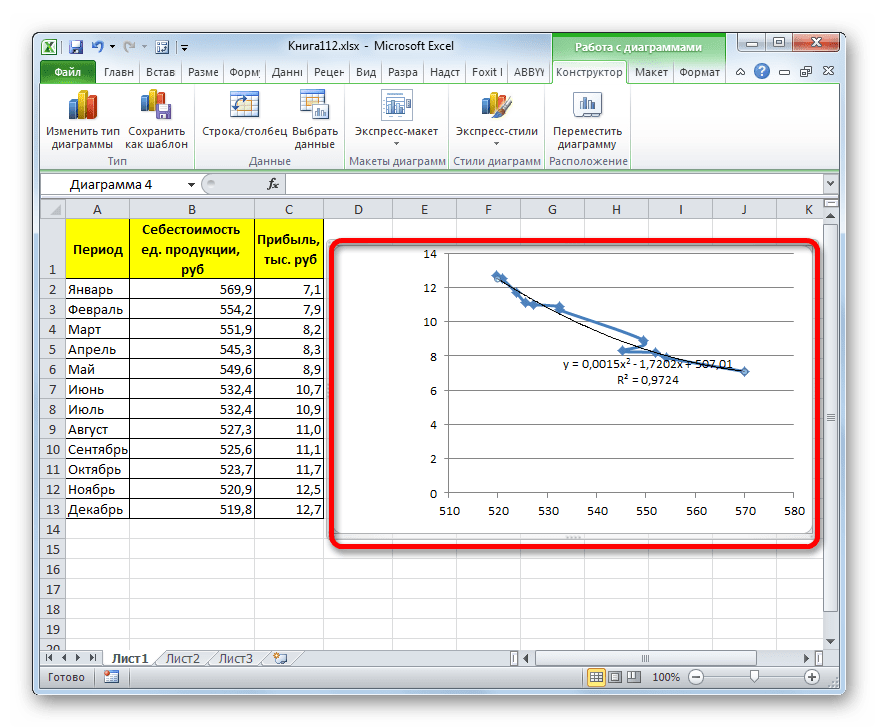
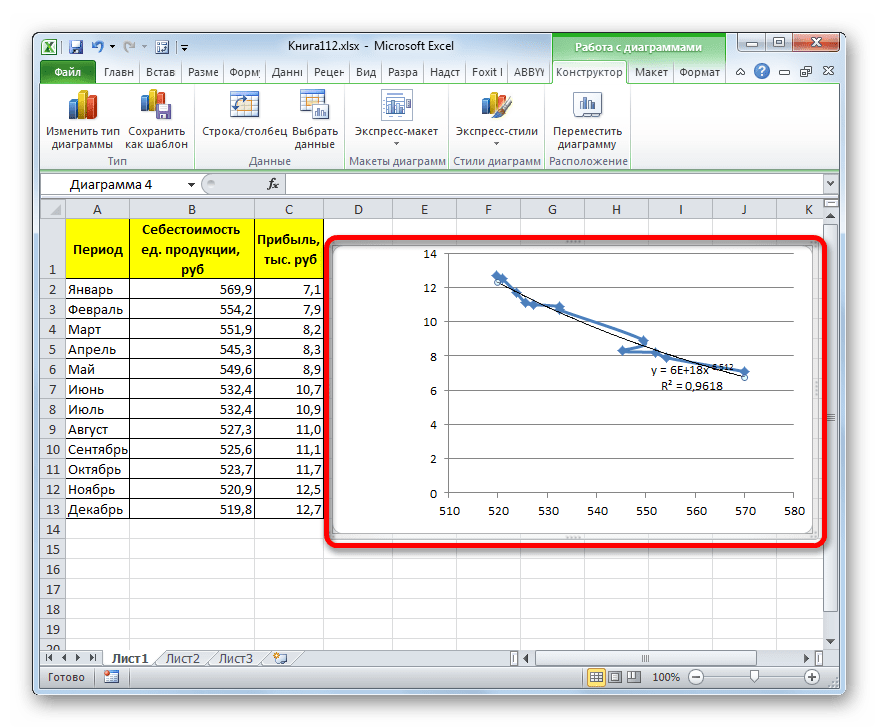
Прежде всего, построим график, на основании которого будем проводить процедуру сглаживания. Для построения графика возьмем таблицу, в которой помесячно указана себестоимость единицы продукции, производимой предприятием, и соответствующая прибыль в данном периоде. Графическая функция, которую мы построим, будет отображать зависимость увеличения прибыли от уменьшения себестоимости продукции.
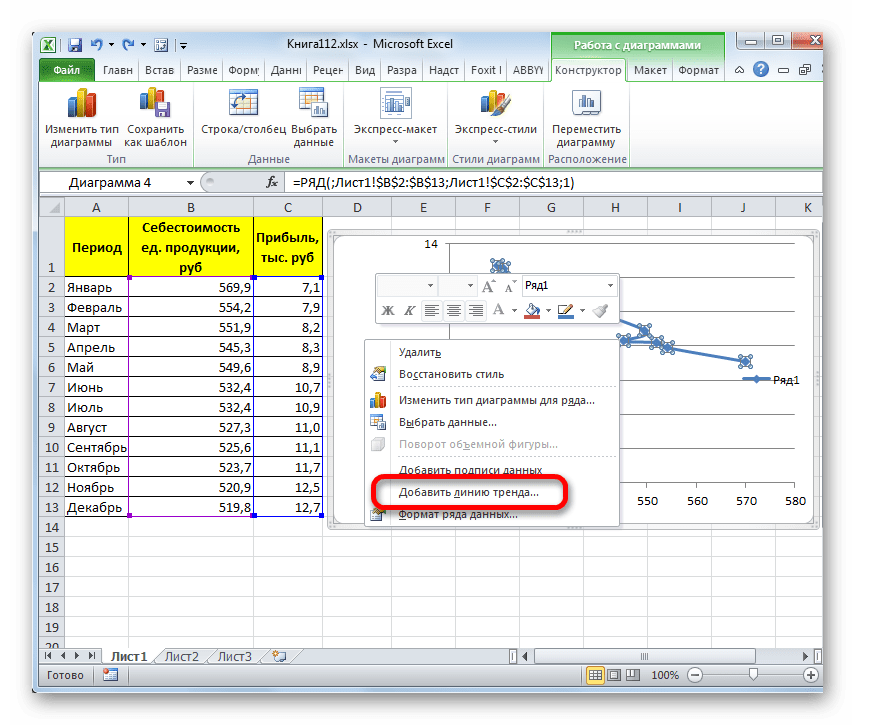
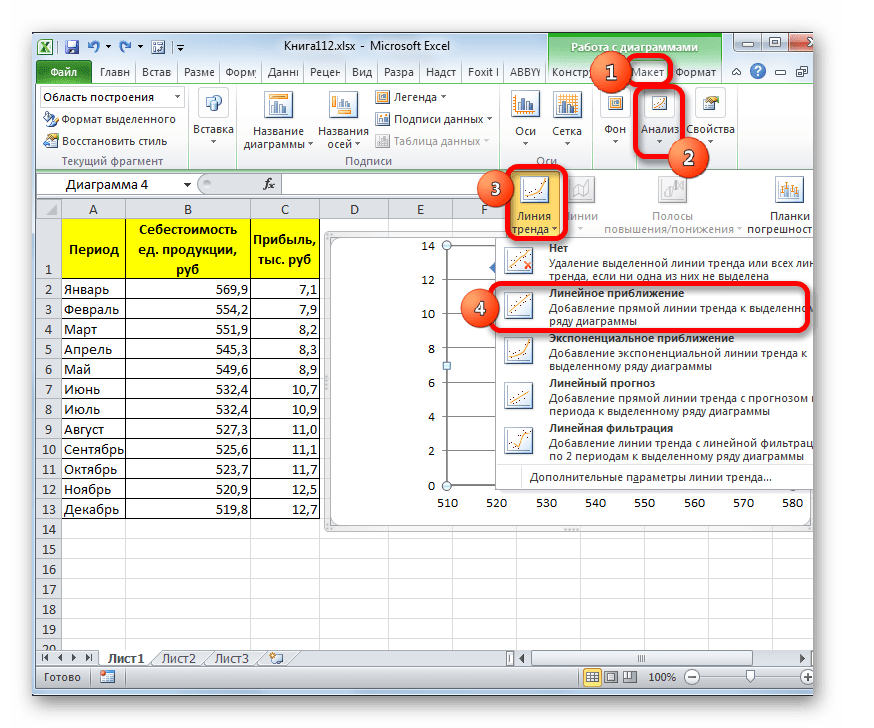
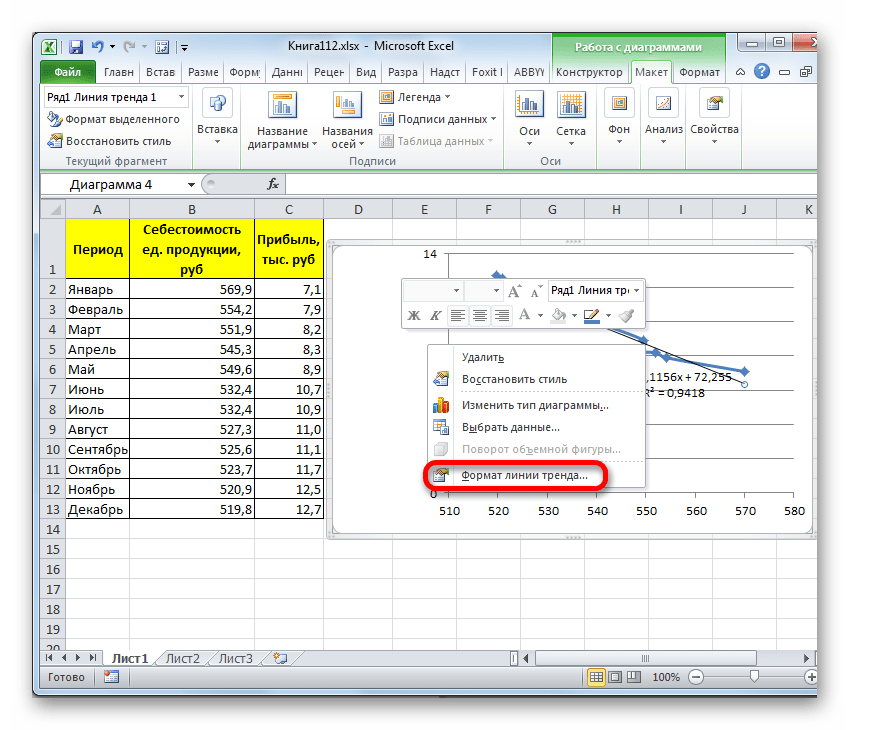
Существует ещё один вариант её добавления. В дополнительной группе вкладок на ленте «Работа с диаграммами» перемещаемся во вкладку «Макет». Далее в блоке инструментов «Анализ» щелкаем по кнопке «Линия тренда». Открывается список. Так как нам нужно применить линейную аппроксимацию, то из представленных позиций выбираем «Линейное приближение».
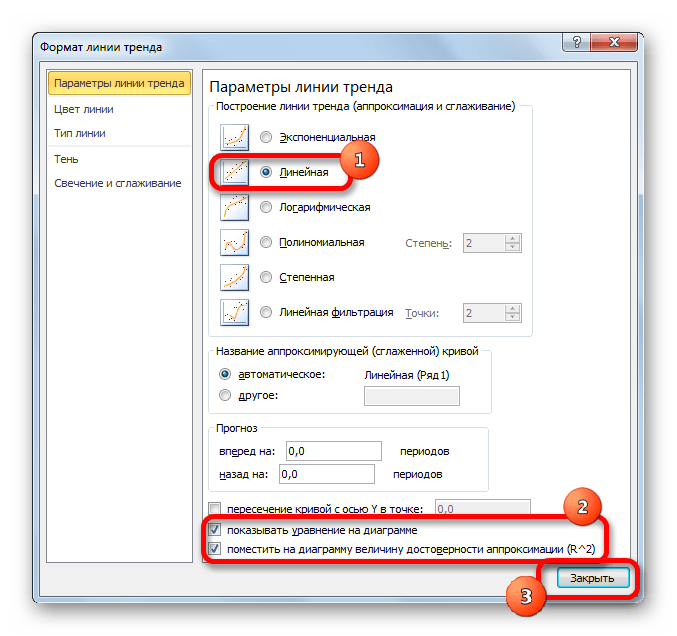
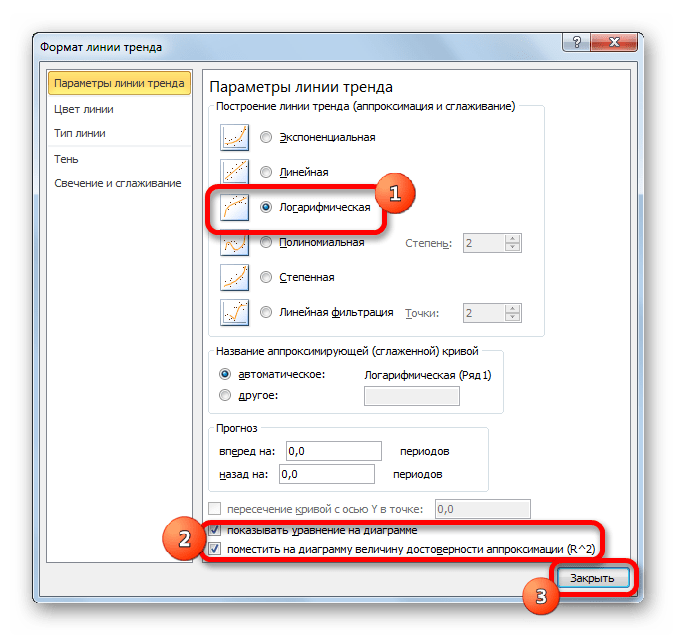
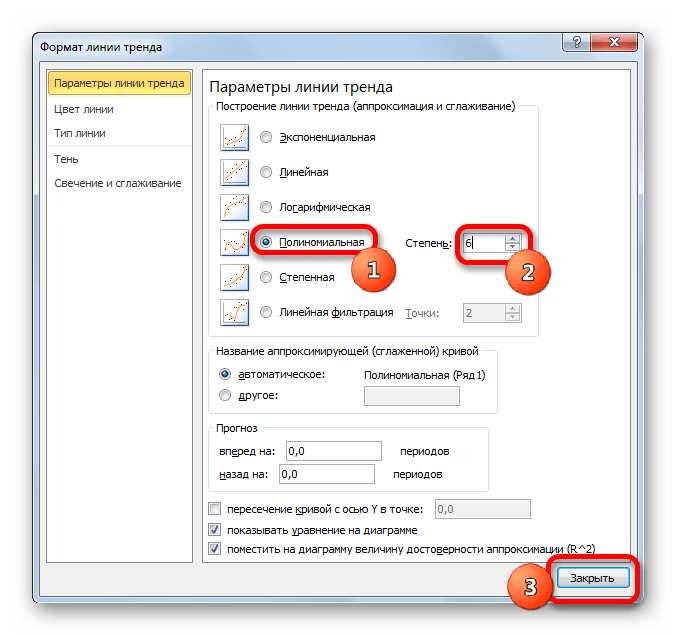
В блоке параметров «Построение линии тренда (аппроксимация и сглаживание)» устанавливаем переключатель в позицию «Линейная».
При желании можно установить галочку около позиции «Показывать уравнение на диаграмме». После этого на диаграмме будет отображаться уравнение сглаживающей функции.
Также в нашем случае для сравнения различных вариантов аппроксимации важно установить галочку около пункта «Поместить на диаграмму величину достоверной аппроксимации (R^2)». Данный показатель может варьироваться от 0 до 1. Чем он выше, тем аппроксимация качественнее (достовернее). Считается, что при величине данного показателя 0,85 и выше сглаживание можно считать достоверным, а если показатель ниже, то – нет.
После того, как провели все вышеуказанные настройки. Жмем на кнопку «Закрыть», размещенную в нижней части окна.
Сглаживание, которое используется в данном случае, описывается следующей формулой:
В конкретно нашем случае формула принимает такой вид:
Величина достоверности аппроксимации у нас равна 0,9418, что является довольно приемлемым итогом, характеризующим сглаживание, как достоверное.
Способ 2: экспоненциальная аппроксимация
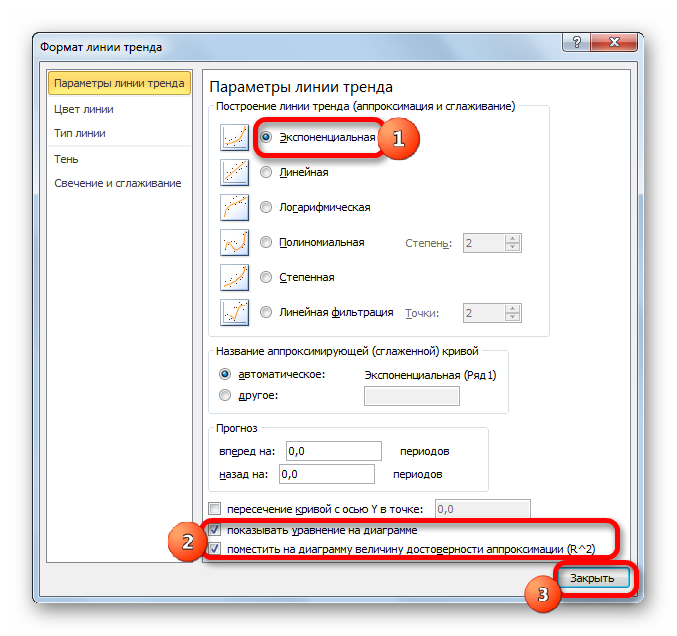
Теперь давайте рассмотрим экспоненциальный тип аппроксимации в Эксель.
Общий вид функции сглаживания при этом такой:
где e – это основание натурального логарифма.
В конкретно нашем случае формула приняла следующую форму:
Способ 3: логарифмическое сглаживание
Теперь настала очередь рассмотреть метод логарифмической аппроксимации.
В общем виде формула сглаживания выглядит так:
где ln – это величина натурального логарифма. Отсюда и наименование метода.
В нашем случае формула принимает следующий вид:
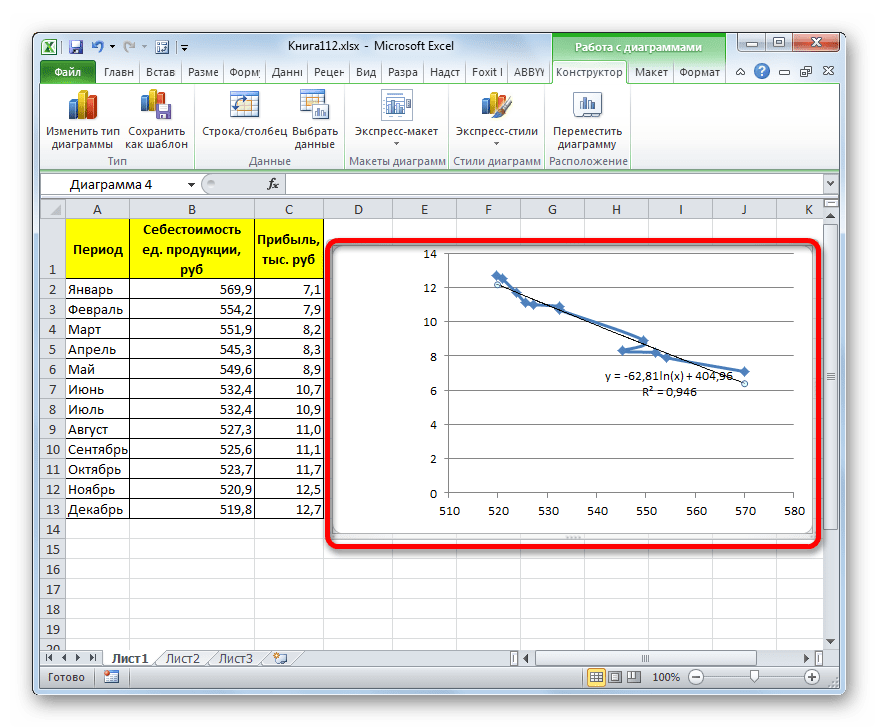
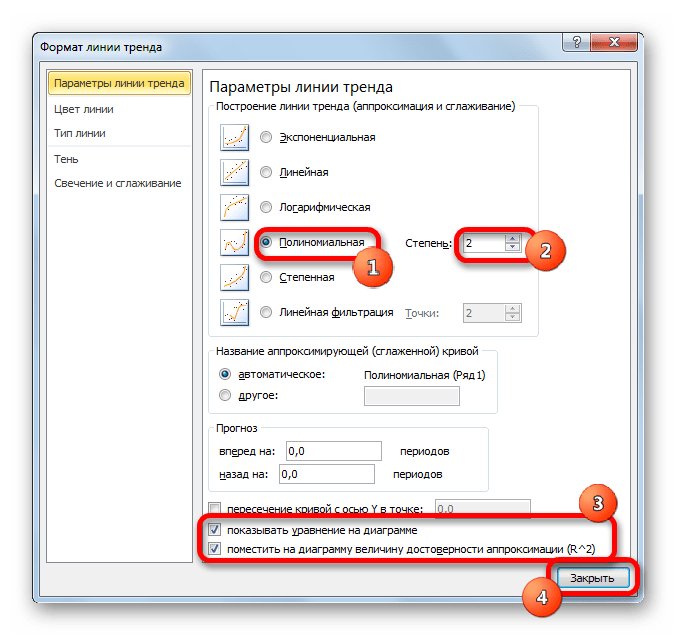
Способ 4: полиномиальное сглаживание
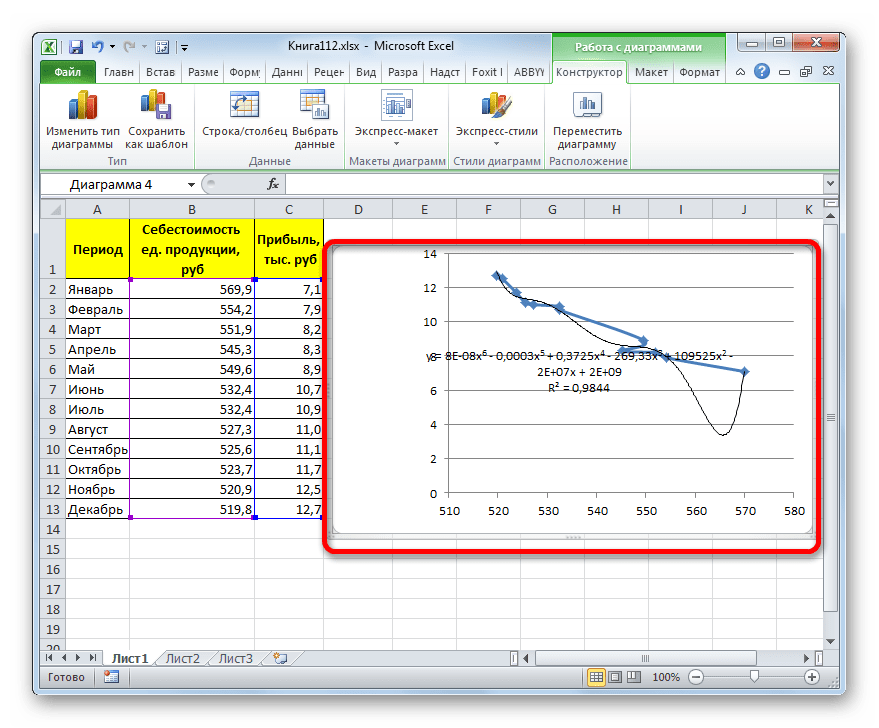
Настал черед рассмотреть метод полиномиального сглаживания.
Данный метод наиболее успешно можно применять в том случае, если данные носят постоянно изменчивый характер. Функция, описывающая данный вид сглаживания, выглядит таким образом:
В нашем случае формула приняла такой вид:
Формула, которая описывает данный тип сглаживания, приняла следующий вид:
Способ 5: степенное сглаживание
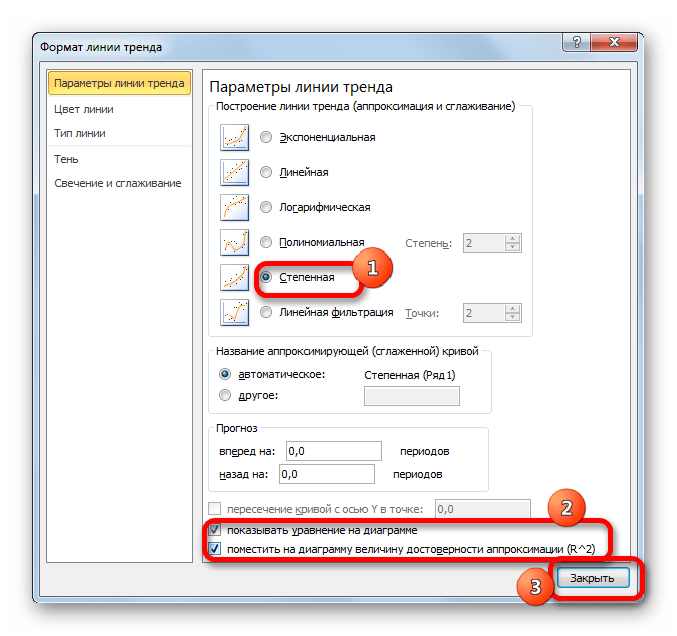
В завершении рассмотрим метод степенной аппроксимации в Excel.
Данный способ эффективно используется в случаях интенсивного изменения данных функции. Важно учесть, что этот вариант применим только при условии, что функция и аргумент не принимают отрицательных или нулевых значений.
Общая формула, описывающая данный метод имеет такой вид:
В конкретно нашем случае она выглядит так:
Как видим, при использовании конкретных данных, которые мы применяли для примера, наибольший уровень достоверности показал метод полиномиальной аппроксимации с полиномом в шестой степени (0,9844), наименьший уровень достоверности у линейного метода (0,9418). Но это совсем не значит, что такая же тенденция будет при использовании других примеров. Нет, уровень эффективности у приведенных выше методов может значительно отличаться, в зависимости от конкретного вида функции, для которой будет строиться линия тренда. Поэтому, если для этой функции выбранный метод наиболее эффективен, то это совсем не означает, что он также будет оптимальным и в другой ситуации.
Если вы пока не можете сразу определить, основываясь на вышеприведенных рекомендациях, какой вид аппроксимации подойдет конкретно в вашем случае, то есть смысл попробовать все методы. После построения линии тренда и просмотра её уровня достоверности можно будет выбрать оптимальный вариант.
Помимо этой статьи, на сайте еще 12419 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
51. Коэффициент достоверности аппроксимации. Оценка надёжности по критерию Фишера.
Коэффициент достоверности аппроксимации это значение которое характеризует точность аппроксимации, т. е. показывает на сколько точно теоретическое распределение описывает реальное распределение.
Коэффициент достоверности аппроксимации R 2 показывает степень соответствия трендовой модели исходным данным. Его значение может лежать в диапазоне от 0 до 1. Чем ближе R 2 к 1, тем точнее модель описывает имеющиеся данные.
Критерий Фишера используется для оценки значимости модели в целом.
Для оценки используется уравнение следующего вида:
где 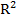
Вычисленное по этой формуле значение сравнивается с критическим значением критерия Фишера из таблиц распределения Фишера:
где 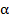
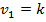
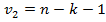
Если в результате сравнения оказывается, что 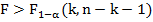
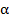
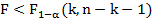

52. Понятие экстраполяции (прогнозирование результатов измерений)
Экстраполяция— это метод прогнозирования, который предполагает, что закономерность развития, действовавшая в прошлом, сохранится и в прогнозируемом будущем.
53. Фундаментальная теорема переноса ошибок имеет вид:
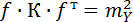
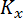
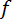
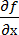
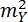
Если оценивается несколько функций, то матрица f будет являться матрицей Якоби (используем формулу 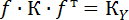
Получим ковариационную матрицу, диагональные элементы которой соответствуют дисперсии, корень из дисперсии будет соответствовать СКО функций.
Если мы имеем функцию суммы или разности двух независимых величин
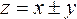
mz 2 =mx 2 +my 2 При 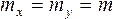
Если функция имеет вид
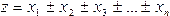
то 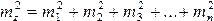
т. е. квадрат средней квадратической ошибки алгебраической суммы аргументов равен сумме квадратов средних квадратических ошибок слагаемых.
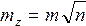
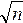
Если функция имеет вид
то 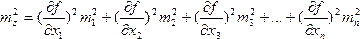
Из формулы (15) следует, что квадрат средней квадратической ошибки функции общего вида равен сумме квадратов произведений частных производных по каждому аргументу на среднюю квадратическую ошибку соответствующего аргумента
54. Оценка точности функций зависимых результатов измерений.
Формулы для вычислений средних квадратических ошибок функции u=f(x1,x2,….xn)
а) в случае некоррелированных аргументов :
mu 2 =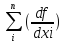
б) для коррелированных аргументов
mu 2 =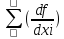
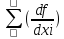
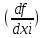
Для системы функций (вектор-функции) u = f(X)
Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.
Коэффициент детерминации или аппроксимации (RI или R2).
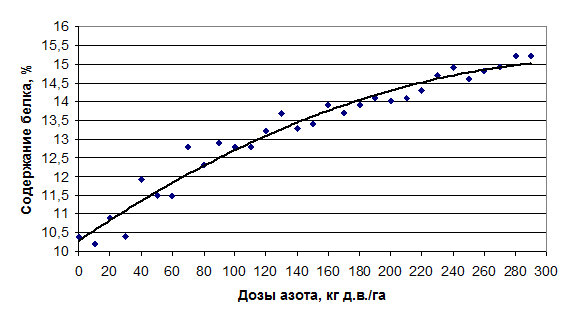
Квадрат коэффициента корреляции (r 2 ) называется коэффициентом детерминации или аппроксимации и обозначается RI или R 2 .Этот коэффициент показывает долю (%) тех изменений, которые в данном явлении зависят от изучаемого фактора. Коэффициент детерминации является более непосредственным и прямым способом выражения зависимости одной величины от другой, и в этом отношении он предпочтительнее коэффициента корреляции. В случаях, где известно, что независимая переменная у находится в причинной связи с независимой переменной х, значение r 2 показывает ту долю элементов в вариации у, которая определена влиянием х. Так, например, если было установлено, что коэффициент корреляции между дозой азотного удобрений и содержанием белка в зерне составил 0,96, то можно утверждать, что 92% (0,96 · 0,96) колебаний содержания белка в зерне обусловлено варьированием доз азотного удобрения.
В практической статистике, коэффициенты детерминации или аппроксимации более широко используются при характеристике изучаемых взаимосвязей. Его можно использовать не только для описания прямолинейной связи между признаками, но и криволинейной (в этом случае, его называют коэффициент аппроксимации, и он представляет собой квадрат корреляционного отношения 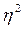
Обычно при определении взаимосвязи между изучаемыми признаками устанавливают последовательно коэффициент корреляции, коэффициент детерминации (или аппроксимации) и скорректированный коэффициент детерминации (RIadj), который рассчитывается по формуле:
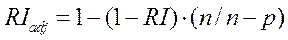
Именно, скорректированный коэффициент детерминации позволяет судить с высокой степенью вероятности о том, насколько процентов варьирование результативного признака обусловлено варьированием факториального.
Множественная корреляция.Корреляцияназывается множественной если на величину результативного признака одновременно влияют несколько факториальных.
Частные коэффициенты корреляции рассчитываются по формулам:
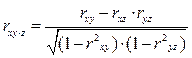
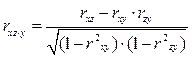
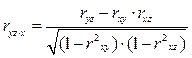
Ошибку и критерий значимости частной корреляции определяют аналогично, что и парной корреляции.
Множественный коэффициент корреляции нескольких переменных – это показатель тесноты связи между одним из признаков (буква индекса перед точкой) и совокупностью других признаков (буквы индекса после точки). Коэффициент корреляции трёх переменных рассчитывается по следующим формулам:
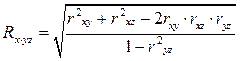
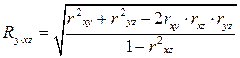
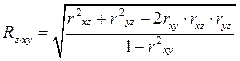
Эти формулы позволяют легко вычислить множественные коэффициенты корреляции при известных значениях коэффициентов парной корреляции. Коэффициент R положителен и всегда находится в пределах от 0 до 1.
Квадрат коэффициента множественной корреляции называется коэффициентом множественной детерминации, который, как и обыкновенный коэффициент детерминации, обозначается RI или R 2 .
Значимость множественной корреляции оценивается по F – критерию:
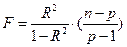
где n – объём выборки,
p – число независимых переменных или признаков.
Теоретическое значение F – критерия берут из приложения III для df1 = р-1 и df2 = n–p степеней свободы и принятого уровня значимости. Нулевая гипотеза о равенстве множественного коэффициента корреляции в совокупности нулю (Н0 : R = 0) принимается, если Fфакт
Регрессионный анализ заключается в том, чтобы отыскать линию (прямую в случае линейной корреляции, параболу первого, второго и т.д. порядка при криволинейной зависимости) наиболее точно выражающую зависимость одного признака от другого. Кроме того, при помощи регрессионного анализа можно выяснить ошибку опытных данных, влияющих на конечные результаты исследования.
Существует множество аналитических методов определения регрессии, которые зависят от типа регрессии (парная или множественная), а также от типа, по которому отмечается взаимосвязь (прямая линия, гипербола, парабола и т.д.).
Парная регрессияхарактеризует связь между двумя признаками: результативным и факторным. Аналитически связь между ними описывается уравнениями:
прямой 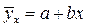
гиперболы
параболы 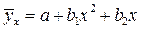
Определить тип уравнения можно, исследуя зависимость графически, однако в практике не часто прибегают к этому методу определения уравнения.
Оценка параметров уравнений регрессии (а, b1, b2…) осуществляется методом наименьших квадратов, в основе которого лежит предположение о независимости наблюдений исследуемой совокупности и нахождении параметров модели при которых минимизируется сумма квадратов отклонений эмпирических (фактических) значений результативного признака от теоретических, полученных по выбранному уравнению регрессии:
SS = 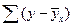
Рисунок 8. Прямая линия регрессии на графике зависимости содержания белка в зерне ячменя от дозы азотного удобрения
Рисунок 9. Параболическая линия регрессии на графике зависимости содержания белка в зерне ячменя от дозы азотного удобрения
В отношении установленной зависимости между дозами азотного удобрения и содержания белка в зерне ячменя данное правило можно интерпретировать так: прямая линия должна быть максимально приближена ко всем значениям ху или ух, что отчётливо отмечается на графике (рисунок 2 и рисунок 3)
Задача регрессионного анализа состоит в том, чтобы установить параметры уравнения регрессии (а, b1, b2…) или иными словами, описать взаимосвязь между изучаемыми показателями с помощью уравнения, оценить на какую величину изменяется значение результативного признака, при изменении факторного на единицу.
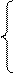
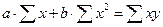
где n – объём исследуемой совокупности (число единиц наблюдений).
В уравнениях регрессии параметр a показывает усреднённое влияние на результативный признак неучтённых в уравнении факторных признаков: коэффициент регрессии b показывает, на сколько изменяется в среднем значение результативного признака при увеличении факторного на единицу собственного измерения. Таким образом, решая данную систему нормальных уравнений задача состоит именно в определении параметров уравнения регрессии a и b.
Уравнение линейной регрессии 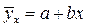
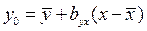
или аналогично для нахождения теоретической линии регрессии х по у: 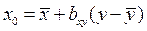
где 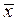
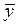
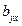
Коэффициенты регрессии вычисляются по формулам:
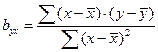
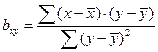
Числители этих формул представляют собой сумму произведений отклонений значений х и у от своих средних (то есть числитель формулы (64) расчёта коэффициента корреляции), а знаменатели – сумму квадратов отклонений от средних. Таким образом, связь между коэффициентов корреляции и коэффициентом регрессии можно математически выразить так:
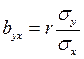
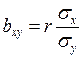
Произведение коэффициентов регрессии равно коэффициенту детерминации:
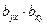
При регрессионном анализе проводят обычно две оценки выборочных коэффициентов регрессии: а) оценки величины отклонений от линии регрессии и б) оценку существенности b, то есть значимость отклонения его от нуля.
Ошибка коэффициента регрессии вычисляется по формуле:
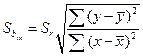

Критерий существенности коэффициента регрессии определяют по формуле:
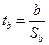
Существенность коэффициента регрессии оценивают по приложению II, число степеней свободы df принимают равным n–2.
ПРИЛОЖЕНИЯ
Значения критерия ω (по Н.Ф. Деревицкому)
| Число степеней свободы | Уровень значимости | Число степеней свободы 5%-ный | Уровень значимости |
| 5%-ный | 1%-ный | 5%-ный | 1%-ный |
| 1,41 | 1,41 | 1,93 | 2,45 |
| 1,64 | 1,72 | 1,93 | 2,45 |
| 1,76 | 1,92 | 1,93 | 2,46 |
| 1,81 | 2,05 | 1,93 | 2,46 |
| 1,85 | 2,14 | 1,94 | 2,47 |
| 1,87 | 2,21 | 1,94 | 4,47 |
| 1,88 | 2,26 | 1,94 | 2,48 |
| 1,90 | 2,29 | 1,94 | 2,48 |
| 1,90 | 2,32 | 1,94 | 2,49 |
| 1,91 | 2,34 | 1,94 | 2,49 |
| 1,92 | 2,35 | 1,94 | 2,50 |
| 1,92 | 2,38 | 1,94 | 2,50 |
| 1,92 | 2,39 | 1,94 | 2,50 |
| 1,92 | 2,41 | 1,94 | 2,51 |
| 1,93 | 2,42 | 1,95 | 2,53 |
| 1,93 | 2,43 | 1,95 | 2,54 |
| 1,93 | 2,44 | 1,96 | 2,55 |
 | 1,96 | 2,58 |
Стандартные значения критерия t (критерия Стьюдента) на 5%-ном, 1%-ном и 0,1%-ном уровне значимости (округлены до десятых)
| Число степеней свободы | Уровень значимости | Число степеней свободы | Уровень значимости | |||
| 0,05 | 0,01 | 0,001 | 0,05 | 0,01 | 0,001 | |
| 12,7 | 63,7 | 637,0 | 2,2 | 3,0 | 4,1 | |
| 4,3 | 9,9 | 31,6 | 14-15 | 2,1 | 3,0 | 4,1 |
| 3,2 | 5,8 | 12,9 | 16-17 | 2,1 | 2,9 | 4,0 |
| 2,8 | 4,6 | 8,6 | 18-20 | 2,1 | 2,9 | 3,9 |
| 2,6 | 4,0 | 6,9 | 21-24 | 2,1 | 2,8 | 3,8 |
| 2,4 | 3,7 | 6,0 | 25-28 | 2,1 | 2,8 | 3,7 |
| 2,4 | 3,5 | 5,3 | 29-30 | 2,0 | 2,8 | 3,7 |
| 2,3 | 3,4 | 5,0 | 31-34 | 2,0 | 2,7 | 3,7 |
| 2,3 | 3,3 | 4,8 | 35-42 | 2,0 | 2,7 | 3,6 |
| 2,2 | 3,2 | 4,6 | 43-62 | 2,0 | 2,7 | 3,5 |
| 2,2 | 3,1 | 4,4 | 63-175 | 2,0 | 2,6 | 3,4 |
| 2,2 | 3,1 | 4,3 | ≥176 | 2,0 | 2,6 | 3,3 |
Наиболее значимые стандартные значения критерия F (критерия Р.Фишера) на 5%-ном, 1%-ном (жирным шрифтом) уровне значимости