что значит кратчайший путь
Как по закону устанавливается кратчайший путь следования к месту отпуска?
Я работаю в ФГБУ «Авиаметтелеком» Росгидромета техником-метеорологом. Предприятие находится на Крайнем Севере. Проживаю тоже на Крайнем Севере. В этом году по льготе Крайнего Севера находилась в отпуске. Маршрут следования указала в заявлении (Мыс Каменный-Сургут-Тюмень-Москва-Симферополь-Керчь и обратно по тому же маршруту. В Тюмени находилась две недели. Бухгалтерия по предоставлении авансового отчёта со всеми проездными документами отказывает мне в оплате полного маршрута следования, оплачивает только до Тюмени, так как считает это местом проведения отпуска, мотивируя это тем, что я использовала не кратчайший путь следования. Правомерно ли это? Заранее благодарна за ответ, Людмила. »
Ответы на вопрос:
Правильно. Потому что вы там были две недели.
Следовательно отпуск проводили там, поскольку иначе непонятно что Вы там делали. Его вам и оплатят (ст. 325 ТК РФ,Закон РФ от 19.02.1993 N 4520-1 (ред. от 07.03.2018) «О государственных гарантиях и компенсациях для лиц, работающих и проживающих в районах Крайнего Севера и приравненных к ним местностях», ст. 33)
Отказ правомерен. Если бы вы ждали единственный возможный стыковочный рейс в Тюмени две недели при отсутствии прямых рейсов, тогда можно было бы попытаться оспорить отказ.
Каких либо ограничений по нахождению в пути нет если это только не связано с отдыхом в нескольких местах.
На этот счет есть Письмо Минздавсоцразвития от 20 февраля 2009 года N 194-13, в котором сказано Следует отметить, что действующее законодательство (ТК РФ и иные нормативные правовые акты) не содержит положений в части ограничения периода нахождения работника в пункте остановки по пути следования от места использования отпуска к постоянному месту жительства. В связи с этим в каждом конкретном случае вопрос о том, проводил ли работник свой очередной отпуск в нескольких местах или следовал через пункты остановки проездом, решается администрацией организации на основании объяснительной записки работника и предоставленных проездных документов.
В этом случае вам необходимо узнать, как регламентируется этот момент вашим региональным законодательством, т.к возможно, там есть какие-то ограничения по количеству дней нахождения в пересадочном пункте.
Согласно ТК РФ Статья 325
Размер, условия и порядок компенсации расходов на оплату стоимости проезда и провоза багажа к месту использования отпуска и обратно для лиц, работающих в государственных органах субъектов Российской Федерации, территориальных фондах обязательного медицинского страхования, государственных учреждениях субъектов Российской Федерации, устанавливаются нормативными правовыми актами органов государственной власти субъектов Российской Федерации
Понятия со словосочетанием «кратчайший путь»
Связанные понятия
В вычислительной геометрии и планировании движений роботов граф видимости — это граф взаимной видимости точек пространства, обычно для множества точек и преград на евклидовой плоскости. Любая вершина в графе представляет точку пространства, а любое ребро представляет прямую видимость между точками. То есть, если отрезок прямой, соединяющий две точки пространства, не проходит через какую-либо преграду, в графе будет нарисовано ребро. Если множество точек пространства лежит на прямой, их можно понимать.
В метрике теории графов выпуклым подграфом неориентированного графа G называется подграф, который включает любой кратчайший путь в G между любыми двумя вершинами. Таким образом, это аналогично определению выпуклого множества в геометрии — такое множество содержит отрезок, соединяющий любые две точки множества.
Построение выпуклой оболочки методом «разделяй и властвуй» — алгоритм построения выпуклой оболочки.
В геометрии конциклическими (или гомоциклическими) точками называют точки, находящиеся на одной окружности. Три точки на плоскости, не лежащие на одной прямой, всегда лежат на одной окружности, поэтому иногда термин «конциклические» прилагают только к наборам из 4 или более точек.
Задача о наибольшей пустой сфере — это задача нахождения гиперсферы наибольшего радиуса в d-мерном пространстве, внутренность которой не перекрывает какое-либо из заданных препятствий.
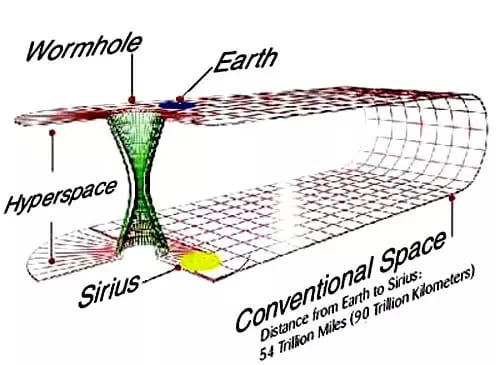
Червоточины могут быть устойчивыми и представлять собой реальные кратчайшие пути в пространстве-времени
Если бы эти структуры были стабильными, это означало бы, что объект, способный выдерживать все механические нагрузки — мог бы перемещаться с экстремальными скоростями между выходом и входом в червоточину, как это, в частности, изображено в некоторых научно-фантастических произведениях («Интерстеллар», если назвать наиболее заметным за последние несколько лет). Эти пространственно-временные связи известны как «мосты Эйнштейна-Розена».
Метрика Эддингтона-Финкельштейна: создание проходимых червоточин
В научной литературе принято считать, что экстремальные силы внутри червоточины заставляют ее растягиваться и разрываться, как резинка, как только она образуется. Но Альберт Эйнштейн и Натан Розен, пионеры этой теории, построили свою модель червоточины на обычной метрике Шварцшильда, и большинство моделей червоточин используют эту же метрику.
Координаты, используемые в их модели, получены преобразованиями (временной переменной) из координат Шварцшильда. И именно эта трансформация приносит главный ингредиент, приводящий к совершенно иному результату, касающемуся устойчивости объекта.
Пересечение горизонта событий черной дыры
«Хорошо известно, что пробная масса, падающая в черную дыру, не достигает горизонта событий ни при каком конечном значении параметров в рамках метрики Шварцшильда, — говорится в исследовании. — Напротив, мы показываем, что горизонт событий достигается при конечном значении переменной времени в рамках метрики Эддингтона — Финкельштейна«.
«Такое поведение не имеет смысла с переменной времени Шварцшильда, поскольку это было бы похоже на продолжение траектории частицы «за пределами времени«», — заключают исследователи в своей работе. Таким образом, они предполагают, что их модель будет более «логичной», чем предыдущие (общепринятые) модели для объяснения поведения червоточины.
Конечно, это не дает неопровержимых доказательств того, что червоточины стабильны и проходимы. Действительно, есть много других факторов, которые следует учитывать помимо общей теории относительности, которые могут продемонстрировать, что такой объект на самом деле «невозможен» или нестабилен вне математических моделей. Модели, которые, кстати, сами заимствуют ряд ярлыков, навязанных ограничениями нашего понимания пространства-времени и действующих сил.
M* — алгоритм поиска кратчайшего пути, через весь мир, на смартфоне
При поиске кратчайшего пути на графах большого размера плохо работает традиционная оценка стоимости т.к. данные заведомо не помещаются в памяти и общая стоимость больше зависит от числа обращений к диску нежели от числа просмотренных рёбер. А число дисковых операций — весьма субъективный фактор, зависимый от сложно формализуемой пригодности графа к хранению на диске в форме удобной для конкретного алгоритма. Кроме того, очень важным становится компактность — количество информации в расчете на ребро и вершину.
Под катом представлена обобщенная эвристика к алгоритму A*, полезная именно в свете практической пригодности на больших графах при ограниченных ресурсах, например, на мобилке.
Итак, наша задача — построение кратчайшего пути по графу из точки в точку. При этом граф достаточно велик, чтобы мы не имели возможности держать его целиком в памяти, а также невозможен предрасчет по сколь-нибудь значительному количеству вершин. Отличный образец — дорожный граф OSM. На данный момент число вершин в OSM превысило 4.6 млрд, общее число объектов — 400 млн.
Понятно, что в таких условиях поиск более-менее протяженного маршрута чистым алгоритмом Дейкстры или Левита невозможен в силу того, что мы не располагаем количеством памяти, необходимым для хранения промежуточных данных.
Как поступает алгоритм Дейкстры?
Фиг.1 Здесь мы видим найденный маршрут и просмотренные при этом ребра.
Проблема в том, что алгоритм Дейкстры не использует никакой информации о свойствах графа и искомого маршрута и при его работе (распространении т.н. «волны») периметр этой «волны» движется от искомой точки во всех направлениях без какой-либо дискриминации.
С другой стороны, на геометрических графах, например, развитой дорожной сети, есть смысл стимулировать распространение «волны» по направлению к цели и штрафовать за остальные направления. Эта идея реализована в алгоритме A*, который является обобщением алгоритма Дейкстры.
В A* стоимость вершины при помещении её в приоритетную очередь не просто равна пройденному пути, а включает еще и оценку пути оставшегося. Как нам получить эту оценку?
Стоит отметить, что это должны быть достаточно вычислительно-дешевая оценка т.к. выполняется она большое число раз. Первое что приходит в голову — вычислить геометрическое расстояние от текущей точки до финиша и исходить из этого, например: осталось 10 км — средняя скорость при движении по городу 20 км/ч, значит наша оценка — полчаса.
При этом, если ребро ведет нас по направлению к финишу, оценка для него будет уменьшаться и компенсировать пройденный путь.
Для ребер, ведущих от цели, эта оценка станет расти, в результате такие точки попадут в очередь с большим весом и вполне вероятно, что до них дело так и не дойдёт.
Примерно такого же эффекта можно достичь, кстати, с помощью техники Beam Search, где принудительно ограничивается размер приоритетной очереди и «недостойные» с точки зрения эвристики кандидаты просто отбрасываются.
Фиг.2 Здесь мы видим поиск того же маршрута с использованием описанной эвристики, почувствуйте разницу.
A* превращается в алгоритм Дейкстры если оценка стоимости возвращает 0, как если бы мы считали, что остаток пути промчимся с бесконечной скоростью.
A* относится т.н. информированным алгоритмам т.к. в эвристике мы используем предположение, что движение в направлении цели скорее приведёт нас к успеху.
Каковы должны быть свойства функции оценки? Она должна быть правдоподобной. Как мы уже выяснили, слишком оптимистичная оценка сводит на нет наши попытки уменьшить просматриваемую часть графа. С другой стороны, слишком пессимистичная оценка заставит алгоритм построить путь строго по направлению, невзирая ни на что. Вряд ли это нас устроит.
Реалистичная оценка должна опираться на свойства графа а лучше на модель данных. Например, вычисляться из уровня загруженности дорог в это время суток и уровня транспортной связности графа. Например, в городе без рек хорошо работает Манхэттенское расстояние.
Но тут сразу возникает масса нюансов:
В жизни геометрически близкие объекты могут быть достаточно удаленными с точки зрения дорожного графа. Например, находиться на разных сторонах реки, горной гряды, моря… В таком случае оценка, основанная на геометрической близости начнёт усугублять ситуацию, упорно направляя «волну» в неправильном направлении.
Фиг.3 Вот так выглядит просмотренная A* часть графа OSM для поиска пути из Италии в Албанию.
Впрочем, это всё равно лучше чем алгоритмом Дейкстры. Хорошо видно как заполнив всю Италию, «волна» начала переливаться через край, набрала скорость и быстро достигла цели.
Фиг.4 А вот так выглядит просмотренная часть графа для алгоритма Дейкстры. По сравнению с ней всё не так уж и мрачно.
А можно ли еще как-то улучшить алгоритм, что по этому поводу говорит Сomputer Sience?
Можно пустить две A* волны навстречу друг другу. Это называется bidirectional search и на первый взгляд кажется очень привлекательной идеей. В самом деле, при хорошей транспортной связности “волна” представляет собой эллипсоид, две малых волны, пущенные навстречу, заметут меньшую площадь по сравнению с одной большой. С другой стороны, возникает проблема обнаружения встречи «волн», точек в их периметрах может быть довольно много и проверять на каждом шагу наличие ребра в чужом периметре не так уж и дешево.
Фиг.5 встречные волны Дейкстры
Возможно, с этим можно было бы и смириться при реальном выигрыше в объеме просмотренной части графа. Но вот если мы рассмотрим вышеописанный пример поиска проезда из Италии в Албанию, то обнаружим, что двунаправленный поиск нам ничем не поможет, а только усугубит ситуацию т.к. кроме заливки всей Италии мы вынуждены будем просмотреть и всю Грецию с половиной Балкан, прежде чем волны встретятся. Ибо вместо одной «волны», упёршейся в препятствие, будем иметь две таковых.
Иерархические подходы
Использование иерархии дорог
Некоторые коммерческие системы, например StreetMap USA, используют для роутинга тот факт, что хорошо спланированная дорожная сеть имеет двухуровневую природу — есть сеть местных дорог и (значительно меньшая) сеть шоссе для поездок на дальние расстояния. Представляется естественным использовать этот факт. Вводятся шлюзы (transit nodes) — вершины, на которых происходит переход из одного уровня в другой. Нахождение “достаточно длинного” пути сводится к нахождению путей от:
Фиг.6 Кусочек StreetMap
Выгоды такого подхода очевидны. Минусы таковы:
Если нет возможности и/или желания выверять граф, остаётся возможность построить иерархию автоматически.
Так или иначе, эксплуатируется идея, что хоть граф и не выверен, тем не менее, атрибуты рёбер позволяют строить маршруты приемлемого качества. Но в силу размеров графа, построение тем же A* в рабочем режиме непозволительно дорого.
Маршрутизация в таком иерархическом графе осуществляется двунаправленным поиском (A* или алгоритмом Дейкстры).
Основной идеей метода является попытка разделения графа на компоненты путём удаления небольшой части ребер — сепараторов. Эти сепараторы и предварительно вычисленные пути между ними образуют следующую иерархию. Утверждается [1], что затратив O(n*log(n)**3) времени и пространства на диске для предварительного расчета, можно выполнять запросы за O(sqrt(n)*log(n))
Grid Based Transit Nodes
Это в общем та же идея с сепараторами, но в целях масштабирования и простоты граф делится на фрагменты решеткой или квадро-деревом, ребра, которые пересекают границы фрагментов становятся транзитными. Понятно, что цена этому — эффективность. В плюсах — высокая автоматизация и как следствие отсутствие человеческого фактора.
На вышестоящих уровнях иерархии в процессе поиска пути не ищутся, а стоимость подсчитывается на основе пред-вычисленных таблиц расстояний между транзитными нодами. Когда маршрут определен, пути восстанавливаются локальным поиском.
Идея метода такова — замечено, что при построении длинных оптимальных маршрутов, «локальные» рёбра посещаются только в самом начале или конце маршрута. Следовательно, построив некоторое количество «обучающих» длинных маршрутов, можно понять, насколько близко расположено то или иное ребро к любому из концов маршрута.
Для некоторого обучающего маршрута P(s…..u.v…. t) вводится показатель reach — минимальное расстояние до концов reach(uv) = min(dist(s…..u), dist(v…..t)).
На всём обучающем множестве reach(uv) — максимальное значение на всех маршрутах, где встретилось ребро (uv).
При «боевом» поиске мы вдали от старта и финиша просто будем стараться избегать рёбер с маленьким значением reach.
Идея метода очень красивая, вопросы вызывает лишь качество обучающей выборки, её достаточность и ресурсы, потраченные на обучение.
Целеустремленные алгоритмы
Граф делится на фрагменты. Проводится обучение построением кратчайших маршрутов между предопределенными точками. При построении обучающего пути, для каждого ребра сохраняется факт, что через него проходит кратчайший маршрут в клетку финальной точки.
Таким образом для каждого ребра мы храним маску флагов, в какие фрагменты графа можно через это ребро добраться кратчайшим путём.
Специфические недостатки этого метода видны невооруженным взглядом:
Из всех вершин выбирается небольшое количество landmarks: λ. В изначальном варианте для каждой вершины предварительно рассчитывались стоимости до каждого λ. Это требовало колоссального количества дополнительной памяти и в дальнейшем требования смягчились и вершины стали группировать.
Поиск в ALT осуществляется как в A*, но оценка оставшегося пути делается на основе рассчитанных стоимостей. Пусть мы рассматриваем ребро (u,v) на пути к целевой вершине t. Для каждой λ в соответствии с неравенством треугольника мы имеем оценку оставшейся части пути (через λ): dist(λ, t) − dist(λ, v) ≤ dist(v, t) и dist(v, λ) − dist(t, λ) ≤ dist(v, t). Минимум для всех λ и даст искомую оценку.
Предварительные итоги
Мы видим два основных направления, в которых идёт развитие:
Кроме того, на аморфных графах попытка построить иерархию может лишь привести к проблемам. Представим себе граф в виде прямоугольной решетки из равнозначных дорог. При движении в некотором направлении правильным решением будет поворачивать в случайном направлении с вероятностью, связанной с направлением. Т.е. если азимут к цели составляет 45°, стоит с равной вероятностью поворачивать направо и налево, чтобы не создавать пробок.
Попытка же построить на такой сетке иерархию приведет к тому, что дорожная сеть станет использоваться неэффективно.
Кроме того, требуется (нелинейное от размера графа) количество дополнительной памяти.
Вот «если бы губы Никанора Ивановича да приставить к носу Ивана Кузьмича, да взять сколь-нибудь развязности, какая у Балтазара Балтазаровича, да, пожалуй…» ©
Справедливости ради стоит сказать, что таких попыток немало, некоторые из них можно найти в списке источников данной статьи. Но мы, конечно же, не изменим себе и придумаем свой собственный, «не имеющий аналогов» метод. ️
Эвристика
Поставим задачу разработать простую и дешевую (и вычислительно и с точки зрения дополнительно хранимой информации) эвристику оценки стоимости пути из одной точки в другую на основе их географических координат. Прямое расстояние не подходит, оно может ошибаться весьма сильно, достаточно посмотреть на Гибралтар и Танжер.
Идея восходит к этой работе.
Фиг.10 — число дорог на квадратный градус в логарифмической шкале
Фиг.11 Оценка стоимости проезда из Нск, чем ближе к оранжевому, тем длинней путь.
Итак, для поиска:
Не беда, в OSM есть тип — береговая линия. Мы растеризуем береговые линии и разрешим ходить из клетки, помеченной как прибрежная, только на «материковые» клетки.

Фиг.12 Береговая линия OSM
Но тут выясняется, что:
Благо, это одноразовая работа, а таких проливов не очень много.
Вот, например, распространение «волны» из Италии, обратим внимание на Гибралтарский пролив.
Фиг.13 Оценка стоимости проезда в Италию, чем ближе к оранжевому, тем длиннее путь.
В целом схема приемлема, но:
Но всё же чувствуется во всём этом какая-то натяжка, поэтому в дело вступает План Б.
План Б.
Фиг.14 Путь, проложенный по верхнеуровневому графу.
Фиг. 11 Хорошо видно, как волна начинает расползаться вширь, когда опорный путь резко меняет направление. Тем не менее, общий объем прочитанных данных весьма невелик. Наблюдается также ускорение в
Итак, на суд читателя представлены два варианта эвристики подсчета стоимости остатка пути для A*.
Для обоих вариантов:
Алгоритм Дейкстры. Поиск оптимальных маршрутов на графе
Из многих алгоритмов поиска кратчайших маршрутов на графе, на Хабре я нашел только описание алгоритма Флойда-Уоршалла. Этот алгоритм находит кратчайшие пути между всеми вершинами графа и их длину. В этой статье я опишу принцип работы алгоритма Дейкстры, который находит оптимальные маршруты и их длину между одной конкретной вершиной (источником) и всеми остальными вершинами графа. Недостаток данного алгоритма в том, что он будет некорректно работать если граф имеет дуги отрицательного веса.
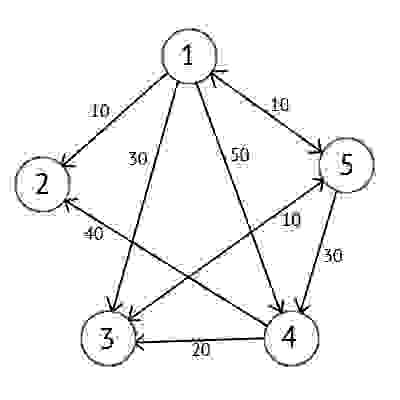
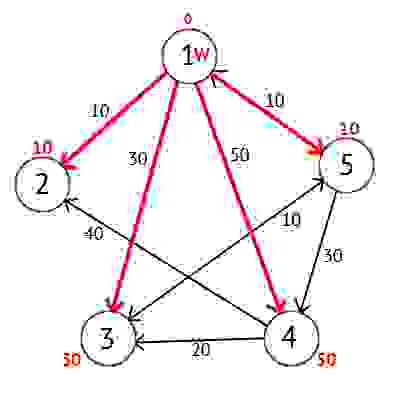
Для примера возьмем такой ориентированный граф G:
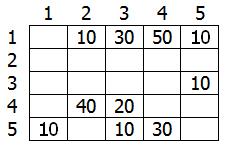
Этот граф мы можем представить в виде матрицы С:
Возьмем в качестве источника вершину 1. Это значит что мы будем искать кратчайшие маршруты из вершины 1 в вершины 2, 3, 4 и 5.
Данный алгоритм пошагово перебирает все вершины графа и назначает им метки, которые являются известным минимальным расстоянием от вершины источника до конкретной вершины. Рассмотрим этот алгоритм на примере.
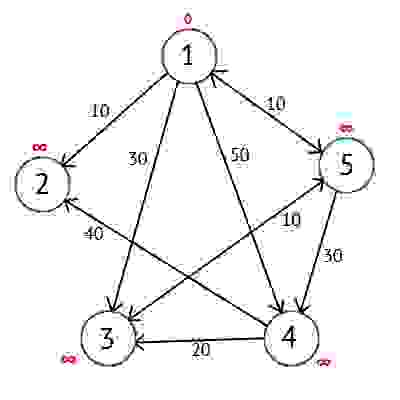
Присвоим 1-й вершине метку равную 0, потому как эта вершина — источник. Остальным вершинам присвоим метки равные бесконечности.
Далее выберем такую вершину W, которая имеет минимальную метку (сейчас это вершина 1) и рассмотрим все вершины в которые из вершины W есть путь, не содержащий вершин посредников. Каждой из рассмотренных вершин назначим метку равную сумме метки W и длинны пути из W в рассматриваемую вершину, но только в том случае, если полученная сумма будет меньше предыдущего значения метки. Если же сумма не будет меньше, то оставляем предыдущую метку без изменений.
После того как мы рассмотрели все вершины, в которые есть прямой путь из W, вершину W мы отмечаем как посещённую, и выбираем из ещё не посещенных такую, которая имеет минимальное значение метки, она и будет следующей вершиной W. В данном случае это вершина 2 или 5. Если есть несколько вершин с одинаковыми метками, то не имеет значения какую из них мы выберем как W.
Мы выберем вершину 2. Но из нее нет ни одного исходящего пути, поэтому мы сразу отмечаем эту вершину как посещенную и переходим к следующей вершине с минимальной меткой. На этот раз только вершина 5 имеет минимальную метку. Рассмотрим все вершины в которые есть прямые пути из 5, но которые ещё не помечены как посещенные. Снова находим сумму метки вершины W и веса ребра из W в текущую вершину, и если эта сумма будет меньше предыдущей метки, то заменяем значение метки на полученную сумму.
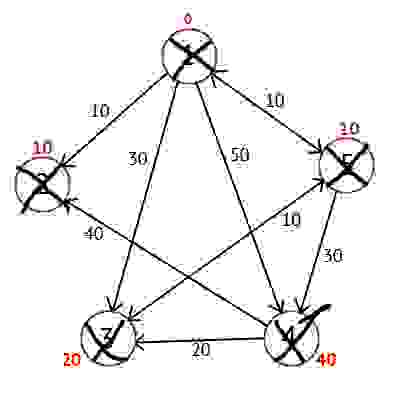
Исходя из картинки мы можем увидеть, что метки 3-ей и 4-ой вершин стали меньше, тоесть был найден более короткий маршрут в эти вершины из вершины источника. Далее отмечаем 5-ю вершину как посещенную и выбираем следующую вершину, которая имеет минимальную метку. Повторяем все перечисленные выше действия до тех пор, пока есть непосещенные вершины.
Выполнив все действия получим такой результат:
Также есть вектор Р, исходя из которого можно построить кратчайшие маршруты. По количеству элементов этот вектор равен количеству вершин в графе, Каждый элемент содержит последнюю промежуточную вершину на кратчайшем пути между вершиной-источником и конечной вершиной. В начале алгоритма все элементы вектора Р равны вершине источнику (в нашем случае Р = <1, 1, 1, 1, 1>). Далее на этапе пересчета значения метки для рассматриваемой вершины, в случае если метка рассматриваемой вершины меняется на меньшую, в массив Р мы записываем значение текущей вершины W. Например: у 3-ей вершины была метка со значением «30», при W=1. Далее при W=5, метка 3-ей вершины изменилась на «20», следовательно мы запишем значение в вектор Р — Р[3]=5. Также при W=5 изменилось значение метки у 4-й вершины (было «50», стало «40»), значит нужно присвоить 4-му элементу вектора Р значение W — P[4]=5. В результате получим вектор Р = <1, 1, 5, 5, 1>.
Зная что в каждом элементе вектора Р записана последняя промежуточная вершина на пути между источником и конечной вершиной, мы можем получить и сам кратчайший маршрут.