что значит квази группа
Значение слова «квазигруппа»
квазигру́ппа
1. матем. алгебраическая структура, напоминающая группу тем, что в ней всегда возможно деление
2. бесструктурное, неорганизованное скопление людей
Делаем Карту слов лучше вместе

Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: заслон — это что-то нейтральное, положительное или отрицательное?
Синонимы к слову «квазигруппа»
Предложения со словом «квазигруппа»
Понятия со словом «квазигруппа»
Отправить комментарий
Предложения со словом «квазигруппа»
Как показывают, однако, эти примеры, границы между группами и квази-группами весьма подвижны и изменчивы: квазигруппы могут постепенно превратиться в группы, как, напр., классы – приобрести партийную организацию, а феминистическое движение – свою ассоциацию.
Разновидности квазигрупп: аудитория, фан-группа, толпа.
Синонимы к слову «квазигруппа»
Карта слов и выражений русского языка
Онлайн-тезаурус с возможностью поиска ассоциаций, синонимов, контекстных связей и примеров предложений к словам и выражениям русского языка.
Справочная информация по склонению имён существительных и прилагательных, спряжению глаголов, а также морфемному строению слов.
Сайт оснащён мощной системой поиска с поддержкой русской морфологии.
СОДЕРЖАНИЕ
Определения
Алгебра
Пустое множество оснащены порожней бинарной операция удовлетворяет это определение квазигруппы. Некоторые авторы принимают пустую квазигруппу, но другие явно исключают ее.
Универсальная алгебра
Другими словами: умножение и деление в любом порядке, одно за другим, с одной и той же стороны одним и тем же элементом, не имеют общего эффекта.
Петли
Петля является квазигруппой с единичным элементом ; то есть элемент e такой, что
Отсюда следует, что единичный элемент e уникален и что каждый элемент Q имеет уникальные левый и правый обратные (которые не обязательно должны быть одинаковыми).
Есть более слабые свойства ассоциативности, которым были даны специальные имена.
Симметрии
Смит (2007) называет следующие важные свойства и подклассы:
Полусимметрия
Квазигруппа полусимметрична, если выполняются следующие эквивалентные тождества:
Хотя этот класс может показаться особенным, каждая квазигруппа Q индуцирует полусимметричную квазигруппу Q Δ на кубе прямого произведения Q 3 с помощью следующей операции:
Триальность
Полная симметрия
Полная антисимметрия
Он называется слабо тотально антисимметричным, если выполняется только первая импликация.
Примеры
Характеристики
Свойство латинского квадрата квазигрупп означает, что для любых двух из трех переменных в xy = z третья переменная определяется однозначно.
Операторы умножения
В этих обозначениях тождества между операциями умножения и деления квазигруппы (указанные в разделе об универсальной алгебре ) следующие:
Латинские квадраты
Бесконечные квазигруппы
Обратные свойства
Каждый элемент цикла имеет уникальную левую и правую инверсию, заданную формулой
Есть несколько более сильных понятий инверсии в циклах, которые часто бывают полезны:
Цикл имеет обратное свойство, если он имеет как левое, так и правое обратное свойство. Петли с обратными свойствами также обладают антиавтоморфными и слабыми обратными свойствами. Фактически, любая петля, удовлетворяющая любым двум из четырех приведенных выше тождеств, обладает обратным свойством и, следовательно, удовлетворяет всем четырем.
Любой цикл, который удовлетворяет левым, правым или антиавтоморфным обратным свойствам, автоматически имеет двусторонние обратные.
Морфизмы
Гомотопия и изотопия
Autotopy изотопия от квазигруппы к себе. Множество всех автотопий квазигруппы образуют группу с группой автоморфизмов в качестве подгруппы.
Спряжение (парастроф)
Левое и правое деление являются примерами формирования квазигруппы путем перестановки переменных в определяющем уравнении. Из исходной операции ∗ (т.е. x ∗ y = z ) мы можем сформировать пять новых операций: x o y : = y ∗ x ( противоположная операция), / и \ и их противоположности. Всего получается шесть квазигрупповых операций, которые называются сопряженными или парастрофами ∗. Любые две из этих операций называются «сопряженными» или «парастрофическими» друг другу (и самим себе).
Изострофа (паратопия)
Обобщения
Полиадические или многомерные квазигруппы
Примером множественной квазигруппы является итерационная групповая операция y = x 1 · x 2 · ··· · x n ; нет необходимости использовать круглые скобки для указания порядка операций, поскольку группа ассоциативна. Можно также сформировать многоарную квазигруппу, выполнив любую последовательность одинаковых или разных групповых или квазигрупповых операций, если порядок операций указан.
Правые и левые квазигруппы
Количество малых квазигрупп и петель
Здесь указано количество классов изоморфизма малых квазигрупп (последовательность A057991 в OEIS ) и петель (последовательность A057771 в OEIS ):
КВАЗИ-ГРУППА
Смотреть что такое «КВАЗИ-ГРУППА» в других словарях:
Алиса в Стране чудес — У этого термина существуют и другие значения, см. Алиса в Стране чудес (значения). Алиса в Стране чудес Alice’s Adventures in Wonderland … Википедия
Использование опросов при оценке программ — Оценить ту или иную программу в широком смысле значит сравнить интересующие показатели до и после проведения программы, на основании чего можно сделать выводы относительно её эффективности. Однако для проведения подобного сравнения… … Википедия
ГОСТ 22670-77: Сеть связи цифровая интегральная. Термины и определения — Терминология ГОСТ 22670 77: Сеть связи цифровая интегральная. Термины и определения оригинал документа: 10. n ичный сигнал электросвязи n агу digital signal Цифровой сигнал электросвязи, имеющий п возможных состояний представляющего параметра,… … Словарь-справочник терминов нормативно-технической документации
Польский поход РККА (1939) — Фотомонтаж Танки РККА переходят Польскую границу Дата … Википедия
ЛОГИКА В РОССИИ — эволюция современной (математической) логики в России. Кон. 19 в. и нач. 20 в. знаменуют выход логики за рамки силлогистики и появление логиков новаторов, таких как П.С. Порецкий, М.В. Каринский, Л.В. Рутковский, СИ. Поварнин, и др. Казанский… … Философская энциклопедия
Приключения Алисы в Стране Чудес — Алиса Лиддел прототип персонажа Алисы, фото Льюиса Кэрролла «Алиса в Стране чудес» (англ. Alice s Adventures in Wonderland) детская книга английского математика и писателя Льюиса Кэрролла. Написана в 1864 году. Есть продолжение «Алиса в… … Википедия
Приключения Алисы в стране чудес — Алиса Лиддел прототип персонажа Алисы, фото Льюиса Кэрролла «Алиса в Стране чудес» (англ. Alice s Adventures in Wonderland) детская книга английского математика и писателя Льюиса Кэрролла. Написана в 1864 году. Есть продолжение «Алиса в… … Википедия
Приключения Алисы в Стране чудес — Алиса Лиддел прототип персонажа Алисы, фото Льюиса Кэрролла «Алиса в Стране чудес» (англ. Alice s Adventures in Wonderland) детская книга английского математика и писателя Льюиса Кэрролла. Написана в 1864 году. Есть продолжение «Алиса в… … Википедия
Польский поход РККА — Не следует путать с Советско польской войной. Польский поход РККА (1939) Вторая мировая война Дата 17 29 сентября 1939 Место … Википедия
Стратегия 2020 — Стратегия 2020 это краткое общепринятое наименование обновленного варианта Концепции долгосрочного социально экономического развития РФ до 2020 года (КДР), подготовленной по заказу российского правительства в 2011 году. Содержание 1 История … Википедия
Социальные группы
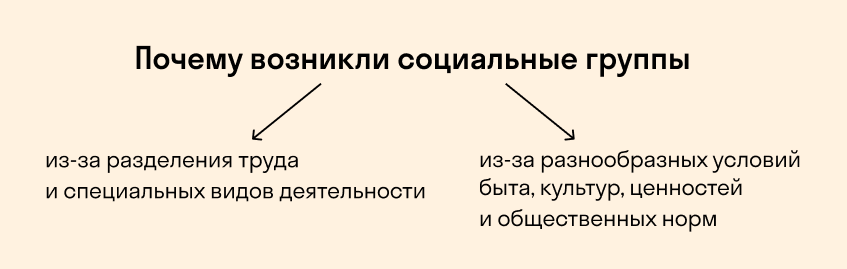
Что такое социальные группы и как они появились
Социальные группы — это устойчивые группы, людей в которых объединяют одни и те же определенные признаки и функции. Например, интересы, положение в обществе, ценности и т. д.
Людей можно назвать социальной группой, если они:
понимают, что входят в конкретную группу;
признают, что другие члены этой группы — тоже ее часть;
взаимодействуют друг с другом внутри своей социальной общности.
Виды социальных групп
Разделить социальные группы на виды можно по нескольким признакам. Всего их 5:
по характеру взаимодействия;
по факту существования;
по способу организации;
по социальному положению.
Рассмотрим, какие бывают группы, в отдельных таблицах.
Люди связаны тесной формой взаимоотношений и заняты общим делом. У всех членов одни и те же цели, поведение и психологические черты. Эта группа — элементарная ячейка общества.
Люди имеют общие цели и деятельность, но не так тесно общаются друг с другом.
Большое количество людей, которое занимает одинаковое положение в обществе и из-за этого связано общими интересами.
Семья, компания друзей, класс в школе и т. д.
Коллеги на работе, соседи по подъезду или улице, население города.
Нация, народность, класс и т. д.
По характеру взаимодействия
Люди внутри группы поддерживают друг друга и связаны личными отношениями.
Люди внутри группы связаны деловыми отношениями и общей целью.
Малые социальные группы — это семья, друзья, одноклассники и т. д.
Средние и большие группы — это коллеги, политические партии, профсоюзы и т. д.
По факту существования
Сообщество людей создали искусственно для учета статистики.
Группу создали по реальным признакам, которые осознают люди.
Пассажиры троллейбусов, покупатели конкретного магазина или товара и т. д.
Жители деревень, школьники, мужчины, женщины, дети и т. д.
По способу организации
Группа, которая существует только в пределах организации.
Группа, которая возникает за счет системы личных отношений и интересов людей.
Группа в университете, одноклассники, коллеги и т. д.
Читательский клуб, музыкальная группа, кружок гончарного искусства и т. д.
По социальному положению
Группа сложилась на конкретной территории. Люди внутри нее связаны общими чертами: языком, культурой, ценностями и т. д.
Нация, народность, раса, племя.
Группа людей, которые живут на одной территории и ведут схожий образ жизни.
Жители города, деревни и т. д.
Группа, внутри которой люди схожи по полу или возрасту.
Мужчины, женщины, молодежь, родители, дети и т. д.
Совокупность людей, в которой члены связаны одной профессией.
Врачи, актеры, инженеры, повара и т. д.
Группа людей, имеющих общие религиозные взгляды.
Синтоисты, христиане, католики, буддисты.
Что такое квазигруппа
В ряду социальных групп разных типов существует и еще одно понятие — квазигруппы. Это название происходит от латинского quasi — мнимый.
Квазигруппа — это малоустойчивая неформальная группа людей, которые взаимодействуют между собой только одним или немногими способами. У такой группы нет четкой структуры, норм и системы ценностей.
Виды квазигрупп
Люди, которых объединяет общий кумир: музыкальная группа, актер или актриса, киберспортивная команда и т. д.
Люди, которые связаны приемом-передачей одной и той же информации в конкретный момент: слушатели в концертном зале, болельщики на стадионе, зрители в кино и т. д.
Временная группа людей, которых объединяет интерес или событие.
Признаки и свойства квазигрупп отличаются от тех, что характерны для других социальных объединений. Рассмотрим их подробнее.
Анонимность. Люди в квазигруппе часто не знакомы между собой, они не ощущают контроля и ответственности перед группой.
Внушаемость. Членам такой группы проще внушить какую-либо идею, чем людям за ее пределами.
Социальная заражаемость. Люди внутри квазигруппы быстрее подхватывают эмоции от других членов и с той же скоростью меняют их.
Бессознательность. Человек внутри квазигруппы становится менее осознанным как личность, поддается инстинктам толпы и может быть непредсказуемым.
Как социальные группы влияют на человека
Мы уже выяснили, какие существуют социальные группы и что они значат в жизни всего общества. Осталось разобраться, что они значат для каждого из членов. Рассмотрим в таблице обе стороны медали — положительные и отрицательные последствия.
У членов группы формируются социальные ценности, каждый учится следовать нормам.
В группах правит мнение большинства. Ради общей цели ее члены могут пожертвовать интересами отдельных людей.
Люди внутри групп развивают коммуникативные навыки: учатся говорить, слышать и слушать.
Группы редко ставят свежий взгляд выше привычного, поэтому подавляют идеи одаренных и творческих членов.
Члены групп помогают друг другу правильно оценивать свои поступки и воспринимать свое «я».
Некоторые члены групп вынуждены идти на внутренний конфликт и соглашаться с ее идеями, которые сами не поддерживают.
В группе человек ощущает, что причастен к общему делу, и более уверен в себе.
Проверь себя
Давайте проверим, насколько хорошо вы разбираетесь в теме статьи. Ниже мы собрали 10 примеров групп людей. Ваша задача — указать виды социальных групп, к которым эти люди принадлежат. Напоминаем, что их может быть сразу несколько.
Коллектив бетонного завода.
Зрители постановки в оперном театре.
Одногруппники в университете.
Прохожие, которые остановились посмотреть на аварию.
Прихожане мечети Кул-Шариф.
Любители музыкальных групп в жанре k-pop.
Пассажиры междугороднего поезда.
Социальные группы во всем их многообразии — это сложная система, в которой предстоит разобраться каждому выпускнику. Чтобы облегчить задачу, предлагаем изучить эту тему вместе с репетиторами Skysmart. На курсах подготовки к ОГЭ и ЕГЭ по обществознанию вы сможете отыскать пробелы в знаниях о социальных группах, познакомиться с заданиями экзамена и сдать его без стресса. Вводный урок — бесплатно.
СОДЕРЖАНИЕ
Определения
Алгебра
Пустое множество оснащены порожней бинарной операция удовлетворяет это определение квазигруппы. Некоторые авторы принимают пустую квазигруппу, но другие явно исключают ее.
Универсальная алгебра
Другими словами: умножение и деление в любом порядке, одно за другим, с одной и той же стороны одним и тем же элементом, не имеют общего эффекта.
Петли
Петля является квазигруппой с единичным элементом ; то есть элемент e такой, что
Отсюда следует, что единичный элемент e уникален и что каждый элемент Q имеет уникальные левый и правый обратные (которые не обязательно должны быть одинаковыми).
Есть более слабые свойства ассоциативности, которым были даны специальные имена.
Симметрии
Смит (2007) называет следующие важные свойства и подклассы:
Полусимметрия
Квазигруппа полусимметрична, если выполняются следующие эквивалентные тождества:
Хотя этот класс может показаться особенным, каждая квазигруппа Q индуцирует полусимметричную квазигруппу Q Δ на кубе прямого произведения Q 3 с помощью следующей операции:
Триальность
Полная симметрия
Полная антисимметрия
Он называется слабо тотально антисимметричным, если выполняется только первая импликация.
Примеры
Характеристики
Свойство латинского квадрата квазигрупп означает, что для любых двух из трех переменных в xy = z третья переменная определяется однозначно.
Операторы умножения
В этих обозначениях тождества между операциями умножения и деления квазигруппы (указанные в разделе об универсальной алгебре ) следующие:
Латинские квадраты
Бесконечные квазигруппы
Обратные свойства
Каждый элемент цикла имеет уникальную левую и правую инверсию, заданную формулой
Есть несколько более сильных понятий инверсии в циклах, которые часто бывают полезны:
Цикл имеет обратное свойство, если он имеет как левое, так и правое обратное свойство. Петли с обратными свойствами также обладают антиавтоморфными и слабыми обратными свойствами. Фактически, любая петля, удовлетворяющая любым двум из четырех приведенных выше тождеств, обладает обратным свойством и, следовательно, удовлетворяет всем четырем.
Любой цикл, который удовлетворяет левым, правым или антиавтоморфным обратным свойствам, автоматически имеет двусторонние обратные.
Морфизмы
Гомотопия и изотопия
Autotopy изотопия от квазигруппы к себе. Множество всех автотопий квазигруппы образуют группу с группой автоморфизмов в качестве подгруппы.
Спряжение (парастроф)
Левое и правое деление являются примерами формирования квазигруппы путем перестановки переменных в определяющем уравнении. Из исходной операции ∗ (т.е. x ∗ y = z ) мы можем сформировать пять новых операций: x o y : = y ∗ x ( противоположная операция), / и \ и их противоположности. Всего получается шесть квазигрупповых операций, которые называются сопряженными или парастрофами ∗. Любые две из этих операций называются «сопряженными» или «парастрофическими» друг другу (и самим себе).
Изострофа (паратопия)
Обобщения
Полиадические или многомерные квазигруппы
Примером множественной квазигруппы является итерационная групповая операция y = x 1 · x 2 · ··· · x n ; нет необходимости использовать круглые скобки для указания порядка операций, поскольку группа ассоциативна. Можно также сформировать многоарную квазигруппу, выполнив любую последовательность одинаковых или разных групповых или квазигрупповых операций, если порядок операций указан.
Правые и левые квазигруппы
Количество малых квазигрупп и петель
Здесь указано количество классов изоморфизма малых квазигрупп (последовательность A057991 в OEIS ) и петель (последовательность A057771 в OEIS ):