что значит min max
Min/Max. Расшифровываем процесс расчёта
При расчёте МИН (минимум или точка заказа), МАКС (максимум) и количества к заказу, используются формулы, основанные на множестве параметров и определённые алгоритмы.
В процессе начального освоения системы автозакупок особенно хочется понимать принципы, по которым производятся эти расчёты. Конечно, все они подробно описаны в документации и отдельно проговариваются в процессе начального обучения, которым в обязательном порядке сопровождается установка Помощника закупок. Однако, когда вы остаётесь один на один со сформированным отчётом и смотрите на конкретную цифру, приходится поломать голову, чтобы понять, откуда она взялась.
К счастью, в помощнике есть возможность расшифровать процесс расчёта. Для это достаточно кликнуть по ячейке МИН или МАКС. Будет открыто окно с комментарием, в котором подробно расписан порядок вычислений, формулы и используемые параметры.
Строка с итоговыми цифрами:
Расшифровка процесса получения этих цифр:

Это пример такой расшифровки.
В первой строке каждого блока выводится результат. Например, МИН_Авто = 1 — это конечный результат расчёта минимума. Сам расчёт выведен чуть ниже, где приведена формула МИН:
Мин = Продано за срок Мин (0.4) + Страховой запас (0.09) + Неснижаемый остаток (0)
ниже расшифровано значение каждого из параметров формулы. Значения каждого параметры указаны в скобках. Например ПроданоЗаСрокМин = 0.4, а СтраховойЗапас = 0.09.
Три логические CSS-функции: min (), max () и clamp ()
Поскольку адаптивный дизайн развивается и становится более детализированным, вместе с ним постоянно развивается CSS и предоставляет авторам больше возможностей для управления состоянием веб-страницы. Функции min(), max() и clamp(), которые теперь поддерживаются во всех современных браузерах, являются одними из последних инструментов, позволяющих сделать веб-сайты и приложения более динамичными и отзывчивыми.
Предисловие
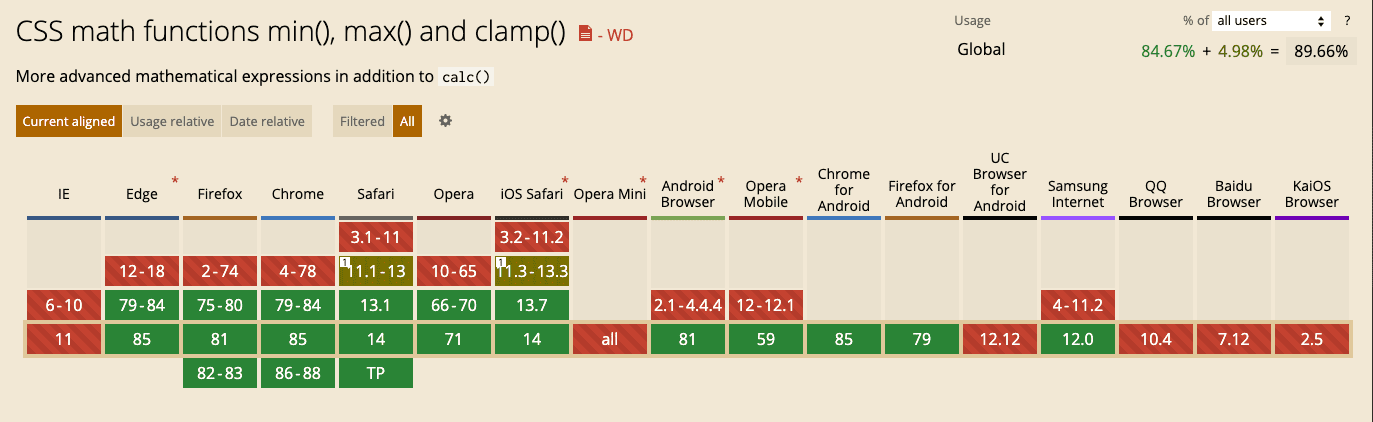
Использование
Посмотрите пример, изменяйте ширину:
Демонстрация выбора функцией min() значения на основе списка параметров и размеров родительского элемента. См. пример.
Функция max() выбирает наибольшее значение из списка выражений, разделенных запятыми.
Демонстрация выбора функцией clamp() значения на основе списка параметров и размеров родительского элемента. См. пример.
Посмотрим ещё несколько примеров.
Идеальная ширина
Согласно «Элементам типографского стиля» (Robert Bringhurst), «любая от 45 до 75 символов ширина рассматривается как удовлетворительная длина строки для страницы с одним столбцом, установленной с шрифтом с засечками и размером текста».
Чтобы текстовые блоки были шириной от 45(минимум) до 75(максимум) символов, можно использовать функцию clamp() и в качестве единиц измерения ch :
Таким образом предлагается браузеру определять ширину абзаца. Он установит ширину 50%. Если 50% окажется меньше 45ch, то будет выбрано 45ch. И, наконец, опять 50%, если это будет больше, чем 75ch.
Использование функции clamp() для ограничения минимальной и максимальной ширины.
Посмотрите пример, изменяйте ширину:
Использование функции min() для ограничения максимальной ширины.
Использование функции max() для ограничения минимальной ширины.
Управление отступами.
Посмотрите пример, изменяйте ширину:
Гибкая типографика
Чтобы обеспечить гибкую типографику, Mike Riethmeuller популяризировал технику, которая использует функцию calc() для установки минимального и максимального размера шрифта, а также позволяет масштабировать от минимального до максимального.
Создание плавной типографики с помощью функции clamp().
С помощью функции clamp() это выглядит элегантнее. Теперь не требуется много кода. Надо только указать минимально допустимый размер шрифта (например, 1.5rem для заголовка), максимальный (например, 3rem) и идеальный размер 5vw, а браузер возьмёт все заботы на себя.
Посмотрите пример, изменяйте ширину:
Таким образом, получаем типографику, которая масштабируется в зависимости от ширины окна просмотра страницы до тех пор, пока не достигнет предельных минимального или максимального значений. Очень компактная строка кода:
Предупреждение. Ограничение размера текста с помощью max() или clamp() может привести к сбою WCAG в 1.4.4 Изменение размера текста (AA), поскольку пользователь может оказаться не в состоянии масштабировать текст до 200% от его исходного размера. Обязательно нужно перепроверять результаты масштабирования.
Заключение
Минимакс на примере игры в зайца и волков

Игра «Заяц и волки»
На шахматной доске есть 4 волка сверху (на черных клеточках), и 1 заяц снизу (на одной из черных). Заяц ходит первым. Ходить можно только на одну клеточку по диагонали, притом волки могут ходить только вниз, а заяц в любую сторону. Заяц побеждает, когда достиг одной из верхних клеточек, а волки, когда они окружили или прижали зайца (когда зайцу некуда ходить).
Перед продолжением чтения, рекомендую поиграть, так будет легче понимать.
Эвристика
В практическом инженерном понимании, метод минимакса опирается на эвристику, которую мы рассмотрим прежде, чем переходить к сути алгоритмов.
В контексте минимакса, эвристика нужна для оценки вероятности победы того или иного игрока, для какого-либо состояния. Задача состоит в том, чтобы построить эвристическую оценочную функцию, которая достаточно быстро и точно, в выбраной метрике, сможет указать оценку вероятности победы конкретного игрока для конкретного расположения фигур, не опираясь на то, каким образом игроки к этому состоянию пришли. В моем примере оценочная функция возвращает значения от 0 до 254, где 0 — победа зайца, 254 — победа волка, промежуточные значения — интерполяция двух вышеуказанных оценок. Оценка вероятности — не вероятность, и не обязана быть ограниченной, линейной, непрерывной.
Пример оценочной функции 1. Чем заяц выше, тем больше у него шансов на победу. Такая эвристика эффективна с точки зрения быстродействия (О(1)), но совершенно не пригодна алгоритмически. «Высота» зайца коррелирует с вероятностью победы, но искажает основную цель зайца — победить. Эта оценочная функция говорит зайцу двигаться вверх, но при небольшой глубине расчета будет приводить к тому, что заяц двигается вверх, не взирая на преграды, и попадает в ловушки.
Пример оценочной функции 2. Заяц тем вероятней победит, чем меньше ему нужно сделать ходов для победы, при замороженных волках. Это более громоздкий алгоритм со сложностью О(n), где n – количество клеточек. Расчет количества ходов сводится к поиску в ширину:
Внимание. Исходники, приведенные в статье, видоизменены таким образом, чтобы читатель смог понять их суть вне контекста основного приложения. Достоверные исходники ищите в конце статьи.
Код, выполняющий поиск в ширину, а точнее заполнение карты значениями равными “расстоянию” от зайца:
Результатом оценочной функции должно быть значение равное «расстоянию» до ближайшей верхней клеточки, либо 254, если дойти до них невозможно. Несмотря на недостатки, которые я опишу ниже, именно эта эвристика используется в игре.
Тем, кто будет смотреть исходники и разбираться — внимание! Архитектура приложения построена таким образом, чтобы оценочную функцию можно было переделать, не затрагивая другие части кода. Но, следует использовать ранее выбранную метрику, иначе алгоритмы не будут понимать показания функции оценки.
Минимакс
Введем некоторые понятия и обозначения:
Метод разработан для решения проблемы о выборе хода с состояния Vi. Логично выбирать ход, для которого оценка вероятности будет максимально выгодной для игрока, который ходит. В нашей метрике, для волков — максимальная оценка, для зайцев минимальная. А оценка считается следующим образом:
Самое время привести пример:
На этом примере, игрок играет зайцем, а компьютер волками. После того как заяц походил, компьютер запускает алгоритм минимакса, на этом примере с глубиной 1. Что делает алгоритм? А кто его знает? Алгоритм перебирает все возможные ходы для волка, и для них получает оценку вероятности победы. Эта оценка, как мы уже говорили ранее, состоит из того же запуска алгоритма минимакса, но уже для других состояний, и уже с ходом другого игрока, и уже с минимизацией, вместо максимизации. Это уже будет второй уровень, последний для указанной глубины 1, от того и дальше алгоритм минимакса не запускается, а возвращает функцию эвристической оценки.
Этот пример будет легче понимать, если рассматривать его снизу. На втором уровне у нас состояния, для которых мы получаем эвристическую оценку (она записана числами). По второму уровню, первый получает свои оценки, соответственно выбрав минимальные значения из тех, что проверены на следующем уровне. Ну и нулевой уровень, выбирает максимальную оценку, из тех, что предоставлены ему первым уровнем.
Теперь, когда у нас есть все оценки, что делать? Радоваться. Нужно выбрать ход. Тут все очевидно, для волка выбирает ход тот, который показывает наибольшую оценку, для зайца тот, который показывает наименьшую. Но ведь оценки для разных ходов могут быть равны, и тогда в идеале нужно выбрать случайным образом, но тут начинаются нюансы. Сразу скажу, что у меня для волка берется первый ход из списка с максимальной оценкой, а для зайца – последний из списка с минимальной оценкой. И это печально, так как достаточно серьезная оптимизация опирается на то, что всегда будет выбираться первый ход из нужного списка. Но для зайца это совершенно не подходит. Дело в том, что волк очень часто (по мере возможностей) ходит так, чтобы оценка была равна бесконечности (254), что делает любой ход зайца “бессмысленным”, и если он будет выбирать любой ход – он будет ходить вниз, либо как попало, а нам нужно заставить его идти вверх, напролом, нарушая фронт волков. Правильно было бы сделать так, чтобы функция эвристики учитывала то, как высоко заяц находится, но с меньшим коэффициентом, чем основная эвристика, но я сделал не так, а как уже описал ранее. Потому и выбирается последний из списка ход, который указывает зайцу идти вверх.
Пример реализации алгоритма:
Внимание! Тут переменная bestMove инкапсулирует много смысла (уточню при запросе), взываю вас никогда не вкладывать столько смысла в 4 бита, если вы не уверены в том, что вы делает все правильно.
Будучи грамотными и образованными людьми, вы уже догадались, что там где есть деревья поиска решений, там есть и клад для оптимизаций. Данный пример не исключение.
Альфа-бета отсечение
Альфа-бета отсечение основано на той идее, что анализ некоторых ходов можно прекратить досрочно, игнорируя результат их показаний. Альфа-бета отсечение часто описывается как отдельный алгоритм, но я считаю это недопустимым и буду описывать его как оптимизирующую модификацию. Альфа-бета относится к классу методов ветвей и границ.
На нашем примере, на втором рисунке, с помощью альфа-бета отсечений, полностью отсекаются 3 нижних ряда, но без самого левого столбца. Я считаю, что это не удачный пример для объяснения, а потому возьму пример из википедии, который чуть более удачный.
Обозначения в примере:
Допустим, для некоторого дерева решений, все дети показывают одинаковую оценку. Тогда можно было бы выбрать из них любую, случайным образом, и это было бы правильно. Но у вас не получится так делать, используя условия alpha >= beta, потому что после первой оценки все остальные могут быть отсечены. Но это не беда, допустим, не будет ваш алгоритм реализовывать стохастическое поведение, это не так важно, но если в вашем алгоритме выбор лучшего из значений с одинаковой оценкой важен, то такое условие отсечения приведет к тому, что алгоритм просто поломается, и будет ходить не оптимально. Будьте бдительны!
Альфа-бета отсечение – очень простой для реализации алгоритм, и суть его сводится к тому, что в функцию минимакса нужно добавить 2 переменные alpha и beta в интерфейс процедуры минимакса, и небольшой кусок кода в ее тело, сразу после получения оценки.
Пример модификации алгоритма минимакса с альфа-бета отсечением (для большей наглядности, внесенные модификации закомментированы, но помните, что это важный код, а не комментарии):
Как я уже говорил ранее, альфа-бета отсечение очень эффективно, и доказательством тому является приведенные ниже показатели. Для каждого случая, на трех разных уровнях глубины расчетов, я замерял количество входов в функцию эвристической оценки (меньше – лучше), и вот что получилось: 
Как вывод, могу сказать что использование этого алгоритма отсечения не только ускорит работу интеллекта, но и позволит повысить его уровень.
Нюансы
Алгоритм делает оптимальные ходы, только если его противник мыслит оптимально. Качество хода в основном зависит от глубины рекурсии, и от качества эвристики. Но следует отметить, что этот алгоритм оценивает качество хода достаточно глубоко, и никоим образом не завязывается (если явно не прописать где-то в эвристике) на количество ходов. Другими словами, если применить этот алгоритм к шахматам, без дополнительных модификаций, он будет ставить маты позже, чем мог бы. А в данном примере, если заяц поймет, что у него нет пути на победу, при оптимальной стратегии волков, он может покончить жизнь самоубийством, несмотря на то, что он мог бы оттягивать проигрыш.
Еще раз, никогда не делайте условием для альфа-бета отсечения alpha >= beta, если вы не на 100% уверены, что для вашей реализации это допустимо. Иначе ваша альфа-бета ухудшит интеллектуальность алгоритма в целом, с высокой долей вероятности.
Алгоритм фундаментальный, в том смысле, что он является фундаментом для большого множества разных модификаций. В том виде, в котором он представлен тут, его нельзя применять для шашек, шахмат, го. В основном модификации стремятся:
Гибкая разметка без медиа-запросов: функции min(), max(), clamp()
С момента появления в браузерах в 2017 году, CSS Grid дал веб-дизайнерам и разработчикам новую суперсилу. На данный момент существует множество статей / руководств, иллюстрирующий возможности и преимущества CSS Grid, описывающих всё – от вдохновлённых ASCII-синтаксисом способом разметки Grid-областей до автоматического размещения элементов, делающих медиа-запросы чем-то устаревшим. Тем не менее, медиа-запросы всё ещё играют важную роль и это не может не вызывать некоторые сложности – наверное.
Проблема с медиа-запросами
На дворе 2020 год и мы ещё никогда не были настолько близки к идее о том, что дизайнеры и разработчики могут контролировать каждый пиксель разметки на любом размере экрана. А с приходом дизайн-систем мы всё чаще мыслим категориями «компоненты», а не «страницы».
Проблема с медиа-запросами заключается в том, что они не очень хорошо вписываются в дизайн-системы, поскольку компоненты в рамках указанных систем обычно определяются без определённого контекста. Компоненты должны, по большей части, вписываться в любой контекст различной ширины и высоты, но медиа-запросы регулируют поведение в соответствии с константой, которая является областью видимости.
Таким образом, медиа-запросов оказывается недостаточно, если мы хотим создать действительно гибкий компонент, который должен вписываться в любой контейнер и иметь собственный набор инструкций о том, как себя вести в разных ситуациях, независимо от внешнего контекста.
В этой статье я рассмотрю, как мы можем создать компоненты гибкой разметки с использование CSS Grid и математических функций для получения большего контроля над гипотетическими инструкциями, которые добавляем в компоненты.
Математические функции
Путаница с именами
Выглядит многообещающе, но поначалу названия этих новых функций могут немного сбивать с толку. Иногда путаница заключается в том, что функция max() используется в значениях свойств, определяющих минимальные параметры (например, когда в свойстве типа min-width используется функция max() ) и наоборот. В подобных ситуациях, из-за изобилия в коде min и max можно спутать, какую именно функцию нужно использовать в данном случае.
Теперь давайте рассмотрим некоторые примеры.
Функции min() и max() принимают два значения. Наименьшее и\или наибольшее значения соответственно, разделённые запятой. Рассмотрим следующим пример с использованием min() :
Здесь мы говорим, что ширина по умолчанию равна 200px, но она не должна быть больше, чем 100% родительского контейнера. Это, по сути, то же самое, что задать:
Довольно гибко, правда? А вот пример с использованием max() :
Данное выражение устанавливает ширину элемента равной 20vw, но не позволяет ей становиться меньше 200px.
Итак, как математические функции могут помочь нам в создании гибких компонентов и разметки в целом.
Базовый пример
Однако, в приведённом выше примере мы можем заметить, что минимальное значение карточки не учитывает ширину области видимости. Если область видимости станет меньше, чем минимальная ширина элементов, карточки исчезают из поля видимости и мы получаем бонус в виде горизонтальной полосы прокрутки. А мы не хотим иметь дело с полосами прокрутки.
Чтобы избежать подобного поведения, мы могли бы добавить медиа-запрос для нужной ширины экрана с изменёнными правилами. Но вместо этого давайте применим наши новоприобретённые знания о математических функциях.
Min() или Max()?
В рассматриваемом случае уместно использовать min()
Мы сообщаем браузеру, что значение должно равняться 350px до тех пор, пока ширина родительского контейнера больше этих 350px. В противном случае берётся значение, равное 100%.
Обратите внимание, что теперь карточки находятся в поле зрения на экранах почти* любого размера.
* «Почти» – потому что контейнер, содержащий карточки, не может стать меньше самого длинного слова.
Получается гораздо лучше. Но можем ли мы сделать еще больше?
Пример с Clamp()
Что если мы хотим немного больше контроля над выделением места для колонок, а также над точкой, в которой должен осуществляться перенос на новую строку? Вместо того, чтобы браузер принимал все решения, используя вышеупомянутую технику автоматического размещения, нам нужен полный контроль.
Скажем, вместо этого мы хотим две колонки на больших экранах и одну колонку, когда область видимости становится меньше определённой ширины, которую мы выбрали – ни больше ни меньше. Легко, правда? Медиа-запросы… да… Нет!
Мы также могли вложить функции наоборот:
В функции мы указываем, что минимально допустимым значением может быть 50%, предпочитаемое значение – 350px, а максимум – 100%.
Если между карточками нужно оставить отступ, мы должны учесть это в наших вычислениях, отняв размер отступа из минимального размера, как показано в примере ниже. Для удобного управления подобными параметрами и поддержания порядка в коде, рекомендую использовать пользовательские свойства.
Можем ли мы пойти еще дальше? Да, можем!
Более математический пример
Что если нам нужно, чтобы три или более колонок элементов перестроились в одну без промежуточных шагов. Это полезно, например, в ситуациях, когда у нас есть только три карточки и хочется избежать ситуации, в которой осуществляется перенос на новую строку из-за одной карточки.
Вы можете подумать, что сделать это будет так же легко, как заменить 50% на, скажем, 33.333% (треть от размера родительского контейнера), создав в конечном счёте три колонки. Если так, боюсь, вы ошибаетесь. При определённой ширине контейнера, достаточно места только для двух карточек, что приводит к образованию двух колонок. Но это не то, что нам нужно.
Расчёты для такой раскладки будут немного сложнее. К счастью, Heydon Pickering уже нашел решение с использванием Flexbox и техники, которую он назвал «Holy Albatross». Он использует преимущества того, как браузер обрабатывает минимальное и максимальное значения. Как сказано в статье Хейдона:
В итоге Хейдон пришел к формуле:
Давайте попробуем реализовать эту формулу в нашем Grid-примере. Применение техники «Holy Albatross» даёт нам что-то вроде этого:
Мы создали то, что называется гибким компонентом, который должен поместиться в любой контейнер с его собственным набором инструкций, определяющих поведение в разных ситуациях.
Инструкция для данной разметки гласит: «Если контейнер по ширине становится меньше 40rem, карточки должны перестраиваться».
Обратите внимание: в приведённом выше Codepen я использовал пользовательские свойства, чтобы сделать код более разборчивым
Контекст, в который помещаются компоненты, не всегда определён строго, поэтому добавляя инструкции, так сказать, в сам компонент, вы в определённой степени гарантируете, что он впишется в любой контекст, независимо от внешних границ. С помощью математических функций мы можем опираться на множество контрольных точек, которые определяются в самих компонентах разметки, как показано в следующем Codepen:
Обратите внимание, что у элементов навигации, средней секции и элементов по бокам свои точки, в которых они перестраиваются. Каждая контрольная точка определяется индивидуально в каждом компоненте разметки, а не одними медиа-запросами для всех.
Почему бы просто не использовать Flexbox?
Дополнительным преимуществом использования CSS Grid вместо Flexbox для такого типа раскладки являются возможности выравнивания, которые мы получаем от Subgrid. Таким образом, мы можем обеспечить выравнивание содержимого (например, заголовков, футера и т.д) отдельных карточек, когда карточки расположены рядом. Вот как это выглядит:
Пока что subgrid поддерживается лишь браузером Firefox 75+.
Другие примеры использования математических функций
Применение математических функций в разметке открывает почти безграничные возможности. Еще одним примером использования математических функций может быть отзывчивый размер шрифта с использованием clamp() и без использования медиа-запросов.
Я вспомнил, как некоторое время назад читал статью об отзывчивом размере шрифта, демонстрирующую удобное математическое выражение для достижения такого же результата. Однако, эта техника требует использования медиа-запросов, чтобы текст не стал слишком большим или слишком маленьким.
Теперь же с помощью математических функций мы можем полностью устранить потребность в них.
Dave Rupert сделал нечто подобное, не прибегая к сложным вычислениям, используя при определении размера шрифта единицы viewport. Используя clamp() можно ограничить диапазон значений, гарантируя, что размер шрифта не станет слишком большим или маленьким.
Это действительно очень умно, тем не менее, при использовании единиц viewport у нас нет такого же уровня контроля. Кроме того, кажется, есть некоторые подводные камни у использования единиц измерения viewport для масштабирования размеров шрифта. Это не будет работать при изменении масштаба браузера, изменение размера окна браузера повлияет на удобочитаемость, а текст на большом экране будет слишком большим.
Поддержка браузерами
Заключение
Опираясь исключительно на область видимости, медиа-запросы могут быть менее гибкими, когда вы работаете с независимыми компонентами разметки. Когда речь заходит о том, как располагать наши элементы, алгоритм автоматического размещения CSS Grid вместе с математическими функциями обеспечивают дополнительную гибкость, и всё это без необходимости явно определять внешний контекст. Предполагаю, что у разметки в вебе большое будущее и с нетерпением жду возможности увидеть дополнительные примеры работы с математическими функциями CSS.

