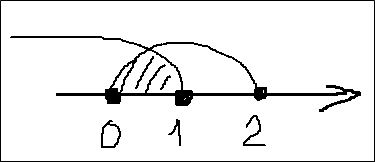что значит перечеркнутый круг в математике
Как пересекать промежутки?
Операции над числовыми промежутками.
Операций над промежутками совсем немного. Всего две. Это пересечение и объединение. При решении серьёзных заданий с неравенствами эти две операции над промежутками необходимо проделывать постоянно. В самых разных сочетаниях. По своей сути это очень простые операции. Но, справедливости ради, эти самые операции являются вторым источником досадных ошибок при решении неравенств после тождественных преобразований. Разберёмся?
Пересекать и объединять числовые промежутки, проще всего при помощи числовой оси. Начнём с пересечения, оно хоть и проще в визуальном восприятии, но простора для ошибок даёт больше…
Как пересекать промежутки?
Сама по себе операция пересечения промежутков совсем простая. Тем не менее, именно пересечение промежутков — самая богатая на сюрпризы операция, которая столько людей ушибла! И очень больно ушибла. Но мы-то с вами — люди думающие и осторожные! С сюрпризами разберёмся, да и под ноги смотреть будем.) И не споткнёмся на ровном месте.
Итак, для начала запоминаем:
Пересечением двух числовых промежутков называется их общая часть.
И всё! Смутить могут только слова «общая часть». Всё просто. Общая часть — это те точки (или кусочки оси), которые одновременно входят в каждый из промежутков. Слова «общая часть» и «одновременно» здесь синонимы. Если раз и навсегда разобраться в этих нехитрых словах, то при ответе на любой вопрос о пересечении любых промежутков вы даже не заметите проблем! Намёк понятен?)
Возможно, вы до сих пор в сомнениях, но картинка с числовой осью, наш главный помощник, всё сразу же прояснит! Это только на конкретных примерах показать можно.
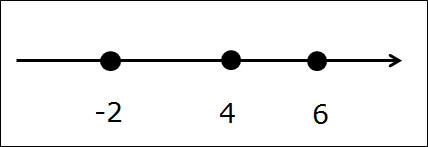
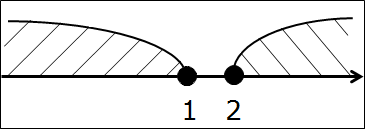
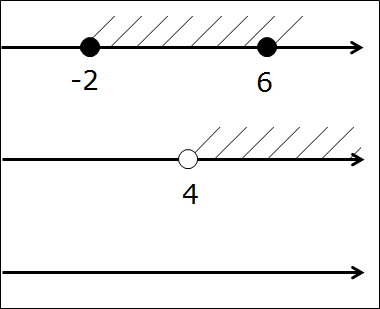
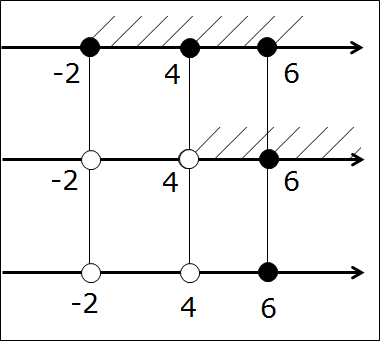
Начнём с совсем простенького, безо всяких подводных камней в виде выколотых точек. Допустим, нам надо пересечь два промежутка:
Первым делом рисуем числовую ось, отмечаем все граничные точки правильными кружочками. Они здесь — чёрные:
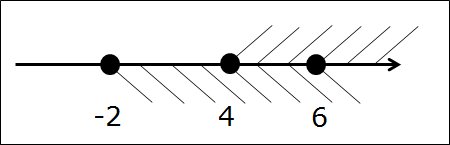
Вот так. Следующим шагом подштриховываем оба промежутка на одной оси. Чтобы не запутаться, для отличия пользуемся штриховкой с разных сторон оси в разных направлениях. Не нужно ювелирно штриховать по линеечке, мы не на черчении. Штрихуем грубо, брутально, но — разборчиво. Где-то штриховки будут встречаться одна под другой, образуя «ёлочку», но ничего не смущаемся, это — именно то, что нам и нужно! Получим такую картинку:
А теперь смотрим и соображаем: какой кусочек числовой оси подштрихован обоими видами штриховки одновременно? Верно! Кусочек между точками 4 и 6. Или — промежуток [4; 6]. Этот промежуток и будет пересечением промежутков [-2; 6] и [4; +∞). И все дела.)
Математически результат пересечения оформляют вот так:
[-2; 6] ⋂ [4; +∞) = [4; 6]
Значок «⋂» означает «пересечение».
Разбираем следующий пример. Пример совсем безобидный, но ступор у некоторых случается, да…)
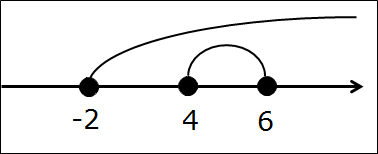
Пересечём, например, промежутки:
Рисуем. В этот раз я буду использовать второй способ рисования — дужки. Получим такую картинку:
И опять соображаем: какой кусок оси содержит точки обоих промежутков одновременно?
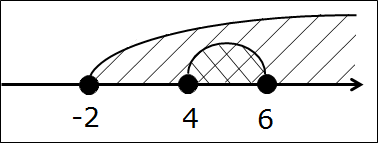
Не догадались? Тогда снова штрихуем промежутки в разных направлениях, прямо под дужками. И смотрим, где штриховки накладываются:
Ну и как, осенило? Да! Второй промежуток [4; 6] — и есть наше пересечение (т.е. общая часть)! Да, весь целиком. Дело всё в том, что второй промежуток, [4; 6], целиком содержится в первом [-2; +∞). Ничего страшного, так бывает.
В математической форме:
[-2; +∞) ⋂ [4; 6] = [4; 6]
Уловили идею? Ну-ка, быстренько закрепим успех!
Найдите пересечения следующих числовых промежутков:
Ответы (в беспорядке):
Что, примитив? Ну да, проще некуда. А вот сейчас начинаются первые сюрпризы! Я же обещал…)
Сюрприз первый — пустое множество
Попробуем пересечь, скажем, такие два промежутка:
(-∞; 1] ⋂ [2; +∞)
Дело нехитрое. Рисуем ось, точки-кружочки, помечаем дужками каждый промежуток, штрихуем, всё чин-чинарём…
И? Где здесь общая часть? А нигде! Нету такого кусочка оси, который был бы закрашен разными штриховками одновременно. На нет и суда нет. В таких случаях говорят, что данные промежутки не пересекаются.
Математически эта фишка записывается вот как:
(-∞; 1] ⋂ [2; +∞) = Ø
Этот перечёркнутый кружочек означает «пустое множество». Множество, в котором нет ни одного элемента. Ни одного числа… Очень частое явление. Особенно — при решении систем неравенств.
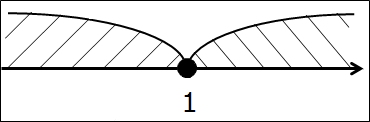
Сюрприз второй — изолированная точка
Всё то же самое, что и в предыдущем примере, только двойку во втором промежутке заменю на единичку. Вот так:
(-∞; 1] ⋂ [1; +∞)
Делать нечего, опять рисуем ось. В этот раз рисуем одну единственную точку 1. Закрашенную.
А здесь какие мысли насчёт пересечения? Да! Единственная общая часть — точка 1. Одна точка. Любая другая точка — правее ли единички, левее ли — попадает лишь в один из пересекаемых промежутков. Либо только в левый, либо только в правый. И только лишь единичка попадает в оба промежутка сразу.
В таких случаях результат пересечения (одна точка) оформляют так:
(-∞; 1] ⋂ [1; +∞) =
Фигурные скобочки в такой записи означают множество. Числовое множество. Единичка внутри фигурных скобок — элемент этого множества. Один-единственный. Или — изолированная точка.
Не следует думать, что пустое множество и изолированная точка –такая уж экзотика при решении неравенств. Такие сюрпризы попадаются в системах неравенств, в методе интервалов, в нахождении области определения функции, в уравнениях/неравенствах с модулем и прочих серьёзных темах. В соответствующих уроках убедимся.)
Кто читает вдумчиво, тот заметил, что слово «множество» я употребил в этом уроке уже не один раз. И это неспроста. Дело в том, что числовые промежутки и операции над ними — это знакомство с ещё одним новым разделом математики, помимо неравенств. Раздел называется «Теория множеств» и работает именно с множествами объектов самой разной природы. Числовыми промежутками, в том числе. Но множества — отдельная большая тема. Не в этот раз…
Полдела сделано. Можно заниматься наскальной живописью. Что-то типа такого:
Несведущий человек отшатнётся в ужасе. А сведущий сразу твёрдой рукой напишет:
(-∞; 1] ⋂ [0; 2] = [0; 1].
Так обычно оформляют пересечение промежутков в большинстве школ. Рисуют ось, штрихуют промежутки, ищут общую часть, да и записывают ответ. Такой способ хорош только в самых простых случаях. Пока точки — чёрные.
Проблемы начинаются с появлением выколотых точек.
Как работать с выколотыми точками?
Как только в игру вступают выколотые (т.е. незакрашенные) точки, вся простота куда-то испаряется напрочь… Особенно, если одна и та же точка в разные промежутки входит по-разному. Где-то она выколота, где-то закрашена… И в каком виде рисовать её на одной оси? Закрашивать её или нет?! Вот и путается народ…
Более того, обратите внимание! Во всех примерах этого урока мы пересекаем лишь два промежутка. Для простоты и понимания сути. А в более продвинутых заданиях (системы неравенств, нахождение ОДЗ и прочие крутые штучки) приходится пересекать и три, и пять… И все с разными кружочками и скобочками… Как не запутаться?
Есть, есть один секретный способ не запутаться! Но о нём — в конце урока.
А пока фиксируем в памяти одну простую вещь:
Операция пересечения — штука жёсткая. Если точка НЕ входит хотя бы в ОДИН из пересекаемых промежутков, то она автоматически НЕ входит и в окончательный результат пересечения.
Поясняю. Если какая-то точка хотя бы в одном из промежутков является выколотой, то нас уже не волнует, что там у неё с остальными промежутками (вторым, третьим, пятым…) — входит она в них или нет: в окончательный ответ такая точка УЖЕ не войдёт. Типа, даже если вы положили в борщ картошку, морковку, свёклу, лук, но в конце посолили стиральным порошком, кушать такой борщ вы уже не будете, да…) Уловили?
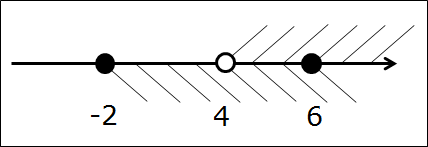
Разберём ценные зелёные слова на практике. Был у нас в самом начале урока примерчик:
[-2; 6] ⋂ [4; +∞)
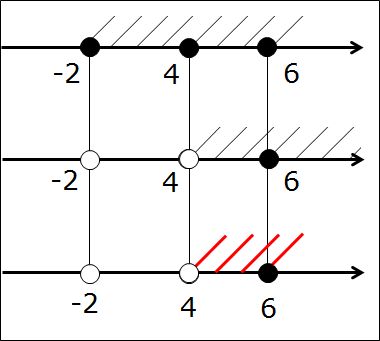
А теперь я немного видоизменю в нём один из промежутков. Сделаю во втором промежутке точку 4 выколотой. Т.е. скобочка перед четвёркой станет круглой. Вот такое пересечение теперь рассмотрим:
[-2; 6] ⋂ (4; +∞)
Рисуем, штрихуем, получаем картинку:
Ищем общую часть, записываем ответ:
[-2; 6] ⋂ (4; +∞) = (4; 6]
Кто в теме и врубился в слова «общая часть» и «одновременно», тот сразу всё понял. А кто не в теме, то… начинаем рассуждать. Примерно так:
А шестёрка? Тут без вопросов: в первый промежуток число 6 попадает на границу, но в закрашенном виде, а во второй (4; +∞) входит явно. Входит одновременно в оба? Да! Рисуем квадратную скобку: …6].
Итого: (4; 6].«
Вот так. Я же говорил, что ключевое слово здесь — одновременно!
Здесь-то ещё просто. А бывает куда злее! Когда неясно, как даже рисовать картинку-то… Например:
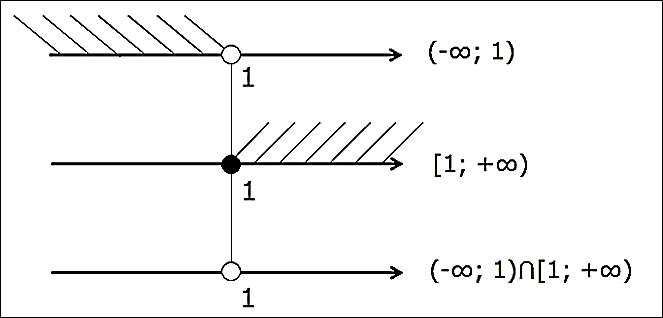
(-∞; 1) ⋂ [1; +∞)
Всё как обычно, рисуем прямую и отмечаем одну единственную граничную точку 1.
И… что-то не рисуется… В первом промежутке единичка с круглой скобкой, во втором — с квадратной. А ось — одна… Каким именно кружочком — пустым или закрашенным — рисовать единицу на оси? Непонятно…
Непонятно, если не понимать сути операции пересечения. А если понимать, то проблем — никаких. Наша граничная точка 1 в первый промежуток (-∞; 1) не входит. Выколота. Стало быть, при пересечении нам уже без разницы, закрашена ли единица во втором промежутке [1; +∞): в окончательный ответ она УЖЕ не войдёт!
Вывод: на оси точка 1 изображается выколотой. Т.е. незакрашенной.
Штриховки нигде не накладываются, а единственная разделяющая точка 1 — выколота. Ответ очевиден — пустое множество:
(-∞; 1) ⋂ [1; +∞) = Ø
Обычно именно так и поступают со всеми подозрительными точками. Берут конкретную точку, поочерёдно подставляют её в каждый из промежутков, анализируют, входит/не входит, и если хоть куда-то не входит — вычёркивают отовсюду. Так рисуются все белые точки. Потом собирают все точки, которые входят одновременно во все промежутки. И рисуют чёрными… И только потом рисуют окончательную картинку… Кошмар? Согласен, кошмар. Когда ось только одна, а точек разной раскраски — много.
Поэтому сейчас мы отдохнём от писанины и тягостных раздумий. А вместо этого — порисуем. Рисовать будем много, но зато результат окупится с лихвой. А количество ошибок резко сократится.)
Обещанный секретный способ!
Пересекаем промежутки без ошибок! Метод параллельных осей.
Итак, снова пересекаем те же самые промежутки: [-2; 6] ⋂ (4; +∞).
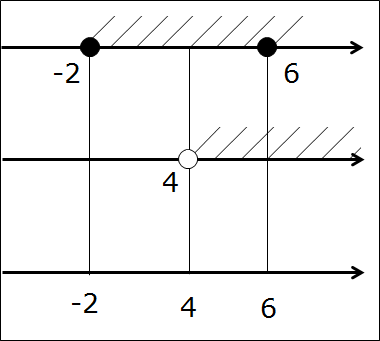
Сейчас берём в руки карандаш и рисуем… три параллельные оси! Всё правильно, именно три, я не обсчитался. На первых двух осях отдельно рисуем и штрихуем те промежутки, которые будем пересекать. Т.е. [-2; 6] и (4; +∞). На каждой из осей — свой. Соблюдаем одинаковый масштаб по всем трём осям! Это важно. Зачем нужна третья ось? Сейчас узнаем.) Получим такую картинку:
Представили? Вот так:
А нужны они нам — эти кружочки-то?! Ещё как! Самый ответственный, третий этап — рисуем нужные кружочки на третьей оси. Для этого рассуждаем так же, как и при прикидке в уме: если на первых двух осях обе точки чёрные, то и на третьей оси точка также чёрная. Если же хоть одна из двух точек выколота — на третьей оси точка также выколота!
Картинка станет вот такой:
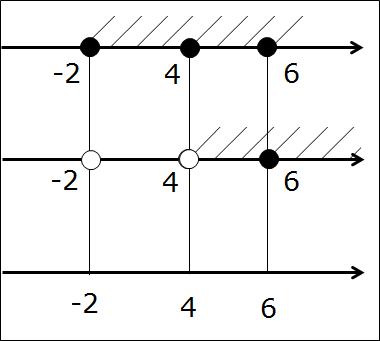
Остались пустяки. Четвёртым этапом штрихуем на третьей прямой тот её кусочек, который заштрихован на первых двух прямых одновременно. Вот так:
Ответ: (4; 6]
Решаем тот самый злой пример с единичкой и пустым множеством: (-∞; 1) ⋂ [1; +∞)
Рисуем картинку с тремя осями и сразу видим всю необходимую информацию:
Безо всяких сомнений ясно, что единичка — выколота, а штриховать на третьей оси и вовсе нечего…
Ответ: Ø
Переходим к следующей важной операции — к объединению промежутков. В следующем уроке…
Ø (латиница)
Ø (латиница)
Это — статья о букве расширенной латиницы Ø. Не следует путать её с ∅ (знаком пустого множества) и с ⌀ (символом диаметра)
| Буква латиницы Ø | ||||||
|---|---|---|---|---|---|---|
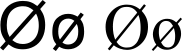 | ||||||
| Латинский алфавит | ||||||
| A | B | C | D | E | F | G |
| H | I | J | K | L | M | N |
| O | P | Q | R | S | T | U |
| V | W | X | Y | Z | ||
| Дополнительные и вариантные знаки | ||||||
| À | Á | Â | Ã | Ä | Å | Æ |
| Ā | Ă | Ą | Ç | Ć | Ĉ | Ċ |
| Č | Ð,ð | Ď,ď | Đ,đ | È | É | Ê |
| Ë | Ē | Ė | Ę | Ě | Ə | Ĝ |
| Ğ | Ġ | Ģ | Ĥ | Ħ | Ì | Í |
| Î | Ï | Ī | Į | İ,i | I,ı | IJ |
| Ĵ | Ķ | Ļ | Ł | Ñ | Ń | Ņ |
| Ň | Ò | Ó | Ô | Õ | Ö | Ø |
| Ő | Œ | Ơ | Ŕ | Ř | ß | ſ |
| Ś | Ŝ | Ş | Š | Þ | Ţ | Ť |
| Ù | Ú | Û | Ü | Ū | Ŭ | Ů |
| Ű | Ų | Ư | Ŵ | Ý | Ŷ | Ÿ |
| Ź | Ż | Ž | ||||
Ø и ø (латинская O диагонально перечёркнутая) — заглавная и строчная буквы, соответственно, используемые в датском, норвежском и фарерском алфавитах. Модификация латинской буквы O.
| ASCII | Юникод | HTML-мнемоника | |
| Ø (заглавная) | D8h | 00D8h | Ø |
| ø (строчная) | F8h | 00F8h | ø |
См. также
Полезное
Смотреть что такое «Ø (латиница)» в других словарях:
Đ (латиница) — Буква латиницы Đ, đ (дьже) Латинский алфавит A B C … Википедия
Ð (латиница) — Буква латиницы Ð, ð (eth) Латинский алфавит A B C … Википедия
латиница — алфавит, письмо, латинский алфавит Словарь русских синонимов. латиница см. латинский алфавит Словарь синонимов русского языка. Практический справочник. М.: Русский язык. З. Е. Алексан … Словарь синонимов
Латиница — наряду с кириллицей (см.) и глаголицей (см.) одна из славянских азбук, представляющая применение букв латинского алфавита для начертания славянских звуков. Первые попытки такого применения известны еще до кириллицы и глаголицы, но эти попытки… … Литературная энциклопедия
ЛАТИНИЦА — см. Латинское письмо … Большой Энциклопедический словарь
ЛАТИНИЦА — ЛАТИНИЦА, латиницы, муж. (филол.). Латинский алфавит, латинское письмо. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
ЛАТИНИЦА — ЛАТИНИЦА, ы, жен. Латинский алфавит. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
Ł (латиница) — Польская буква Ł Латинский алфавит A … Википедия
Æ (латиница) — Лигатура Æ Латинский алфавит A … Википедия
IJ (латиница) — Нидерландская буква IJ Латинский алфавит A … Википедия
Œ (латиница) — Латинский алфавит A B C D E F G H I J K … Википедия
Что означает буква “R” в кружочке в конце названия многих продуктов?
Что значит перечеркнутый кружок в математике
Бірінші бассейнде 1600м3, екінші бассейнде 1215м3 су бар. Бірінші бассейнді тазарту үшін одан сағатына 65м3 су насоспен сыртқа ағызылды. Екінші бассей нге сағатына 45м3 су насоспен құйылды. Екі насос жұмыстарын бір уақытта бастаса, неше сағаттан соң екі бассейндегі су көлемі теңеседі? 2+7=? Сколько получитса скажите поже На всё пожалуйста ответьте плииииз 15 баллов Найдите наибольшее целое число, при котором выполняется неравенство: x ≤ −64,4 Сравните a и –b, если a и b отрицательные числа. В записи чисел стерли несколько цифр и вместо них поставили звездочки. Сравните эти числа: А) −4,2** и −5,3** Б) −93* и −8** В правильной четырёхугольной пирамиде SABCD (с вершиной S) сторона основания равна √2, а боковое ребро равно 2. Найдите расстояние от точки A до прямо й SC. СРОЧНО НАДО СДЕЛАЙТЕ ПЛИЗ! Помогите пожалуйста. А куб с ребром 1 м разрезали на кубики с ребром 1 дм и сложили их в ряд Какой длины получился ряд Расположите числа в порядке возрастания: −6; 5,4; 0,7; −5,3; 0; −16; 4,7 Куб с ребром 1 м разрезали на кубики с ребром 1 дм и сложили их в ряд Какой длины получился ряд 2.Вынести общий множитель за скобки а) 8a⁴b² — 12a²b³ + 4a² б) x(y — 5) — 6(5 — y)
Символ, обозначение и значок диаметра: три способа его вставки
На компьютерной клавиатуре присутствуют не все символы. Нет на ней и символа диаметра. Общепринятое обозначение диаметра выглядит следующим образом — «Ø». Но при этом существует масса способов вставить его во многих различных приложениях. Наиболее популярным среди них является использование кодов ASCII. Второй способ связан с офисным пакетом компании Microsoft и работает только там. Третий метод это применение буфера обмена. Для его исполнения нужен непосредственно сам значок диаметра, который при помощи функции «копирования» и «вставки» будет вставлен в нужное приложение.
Все способы будут подробно рассмотрены и представлены в этой статье.
Обозначения на бирках одежды
На этикетке каждой фирменной вещи производитель перечисляет значки, которые помогут правильно ухаживать тканью. Они делятся на 4 большие группы:
Каждому значку соответствуют особые условия обработки вещей. Например, перечеркнутый символ таза означает, что стирка в вое в любом виде запрещена – она испортит ткань.
Важно! Чтобы одежда оставалась чистой и не повреждалась в процессе ухода, используйте информацию на значках комплексно – учитывайте все перечисленные на бирке.
В каких ситуациях появляется потребность символа диаметра?
Существует масса ситуаций, при которых появляется такая потребность вставить знак «Ø» в нужный электронный файл. Для примера, он может потребоваться при составлении чертежей, детальном оформлении прайс-листов, оформлении рекламных продуктов или обозначения трубных изделий или запорной арматуры. Ученики, студенты или работники всяческих учреждений, предприятий либо организаций повседневно используют данный знак в процессе своей учебной, либо трудовой деятельности.
Перечислять примеры применения значка диаметра можно бесконечно долго, но и так понятно, что в некоторых ситуациях без него приходится достаточно трудно либо не комфортно. Именно поэтому далее по тексту мы рассмотрим три способа вставки символа диаметра в электронный документ.
Первый способ
Самым популярным способом можно назвать использование кодов ASCII. Он может быть осуществлен непосредственно самой ОС Windows. Для его реализации важно знать код – «0216», который в таблице кодов ASCII распознается как знак «Ø». Алгоритм ввода будет таковым:
Главное достоинство данного способа это то, что он универсален. Он может работать во многих существующих приложениях. Особенность способа состоит в том что сам символ, в качестве исходника не нужен. Недостаток данного метода в том, что всегда нужно знать код.
Второй способ
Программа Word и другие приложения взаимозаменяемый метод ввода «Ø» связан с определенным набором таких программных приложений, как: Microsoft Office Word, Excel и других. Для примера введем знак диаметра в » Word». В других случаях алгоритм ввода будет аналогичным. Во время работы заходим на панель инструментов на вкладку «Вставка». Она расположена в верхней части экрана между закладками «Главная» и «Разметка страницы». Наводим на эту вкладку курсор мыши и кликаем один раз левой кнопкой. После этого в правой части экрана видим панель «Символы». Там выбираем строку «Символ» и в появившемся списке нажимаем «Другие символы». Все эти действия осуществляются правой кнопкой мышки.
Теперь можно наблюдать открывшееся окно вставки. Находим нужный нам знак «Ø» за счет прокрутки найденных символов. В этом нам поможет колесо мыши. После удачного поиска «Ø», выделяем его одним нажатием левой кнопки мыши и кликаем кнопку «Вставить». После этого закрываем окно. Затем наверняка появиться значок диаметра в Word (в рабочей зоне). Отрицательная сторона данного способа в том, что он будет работать только в одной группе программных продуктов. Поэтому везде его применить невозможно.
Третий способ
Так же одним из способов вставки «Ø» является применение буфера обмена и использование функций «Копировать» и «Вставить». Буфер обмена это определенная часть памяти компьютерной операционной системы, которая предназначена для временного хранения информации. Сначала требуется найти где-нибудь такой символ.
В качестве примера, можно значок диаметра вставить в ворд (word) в соответствии с вышеизложенным алгоритмом. После чего его выделяем и копируем (по желанию можно использовать так называемые горячие клавиши «Ctrl»+»C»). Затем заходим в иное приложение и осуществляем действие вставки («Ctrl»+»V»). Отрицательная сторона данного способа заключается в том, что в любом случае нужен исходный символ. А так бывает далеко не всегда.
Каждый пользователь может выбрать для себя наиболее подходящий способ вставки символа (знака) диаметра — «Ø», учитывая свой индивидуальный подход и персональные навыки.
Буфер обмена
Еще один способ вставки «Ø» базируется на использовании буфера обмена и сочетания операций «Копировать» и «Вставить». Для начала нужно найти где-то этот символ. Например, можно вставить значок диаметра в «Ворде» в соответствии с ранее изложенной методикой. Затем его выделяем и копируем (можно использовать сочетание клавиш «Ctrl»+«C»). Потом переходим в другое приложение и используем операцию вставки («Ctrl»+«V»). Минус такого решения заключается в том, что нужен исходный символ. А он не всегда есть в наличии.
Математические знаки
В разделе собраны математические символы, которые невозможно корректно отобразить с помощью ввода на клавиатуре. Весь представленный набор можно разделить на несколько групп:
Использование данных иконок – единственный вариант корректного отображения ряда математических символов на сайте или в сообщении в любой операционной системе конечного пользователя. Достаточно лишь скопировать закодированный значок. Применение изображений для этих целей значительно усложняет процесс, требует подгонки при разработке и наполнении интернет-ресурса. Кроме того, медиа-контент занимает большой объем дискового пространства.
Математические символы подойдут для публикаций в социальных сетях, создания сообщений в чатах и форумах, разработки интернет-страниц.
Математика, как язык всех наук, не может обходиться без системы записи. Многочисленные понятия, и операторы обрели своё начертание по мере развития этой науки. Так как в стандартные алфавиты эти символы не входят, напечатать их с клавиатуры может оказаться проблематично. Отсюда можно скопировать и вставить.
Консорциуму Юникода не чужды проблемы учёных, поэтому в таблицу было включено множество различных знаков. Если тут нет того, что нужно, воспользуйтесь поиском по сайту или посмотрите в разделах математические символы, разнообразные математические символы-A, разнообразные математические символы-B, дополнительные математические операторы. Буквы для формул можно взять в наборе греческие буквы и блоке математические буквенно-цифровые символы.
Числа для степеней составляются из маленьких цифр. Там же собраны дроби.
Что значат символы
Основная символика для информирования потребителей о правилах ухода за конкретным изделием разработана международными организациями и зафиксирована в стандартах международной системы ISO. Обозначения в виде пиктограмм наносятся на ярлыки, которые надёжно крепятся к одежде.
На ярлыке в форме пиктограмм размещена сложная инструкция по уходу за одеждой. Понимая значения символов, вы всё сделаете правильно.
Символы размещаются в строго установленном порядке, при этом возможно применение более одного знака для процесса, если нужно уточнить условия ухода за изделием. Кроме символов могут быть и надписи, поясняющие и уточняющие тонкости чистки.
Есть пять основных обозначений для основных способов по уходу за предметами из вашего гардероба:
– эта картинка используется, чтобы информировать владельца о допустимых параметрах стирки изделия. Если внутри этого знака проставлено число – это температура воды, при которой следует стирать вещь.
– этот знак обозначает процесс сушки (и отжима). В этом квадрате дополнительные символические обозначения устанавливают, как можно отжимать и просушивать изделие.
– о смысле этого символа легко догадаться. Дополнительные точки и штрихи на этом «утюжке» задают температурный режим глажки.
– этот значок информирует потребителей о том, допустимо ли применять отбеливание, а дополнения к нему конкретизируют условия процедуры.
– здесь показывается, разрешена ли профессиональная химчистка. А буквы и дополнительные штрихи на картинке адресованы её работникам. Они указывают, рекомендована сухая или влажная чистка и какие химические вещества допустимо применять.
В системе основных условных обозначений применяются также значки:
Все дополнения к приведённым выше картинкам показаны в таблице с вариантами значений символов и их расшифровкой.
Производители одежды из разных государств дополняют их своими пиктограммами. Делается это в интересах заботливых хозяек, желающих в точности соблюсти рекомендации по уходу за одеждой.
Детальное описание знаков на ярлыках
Ниже будет приведено детальное описание знаков, присутствующих на ярлычках, а также их полная расшифровка: