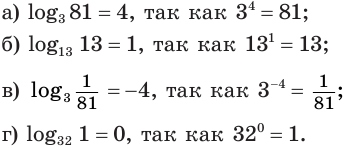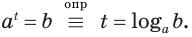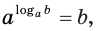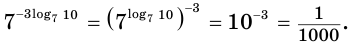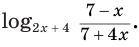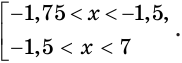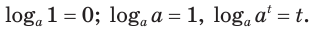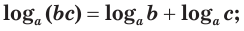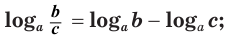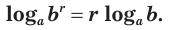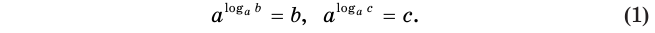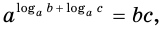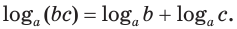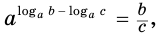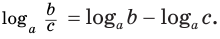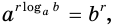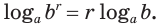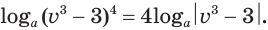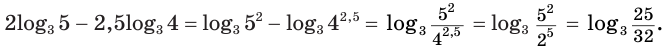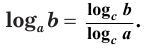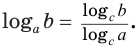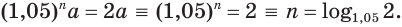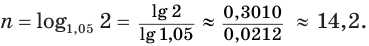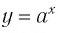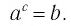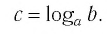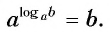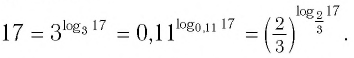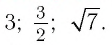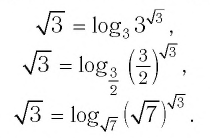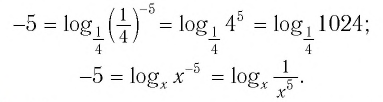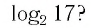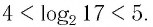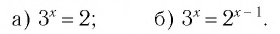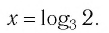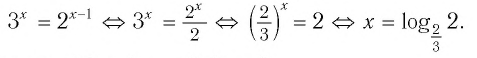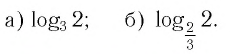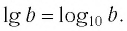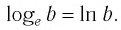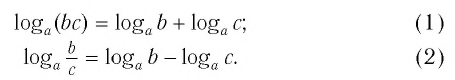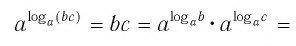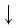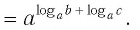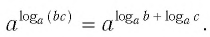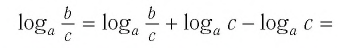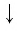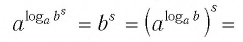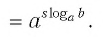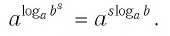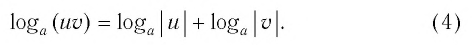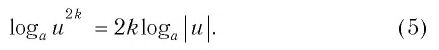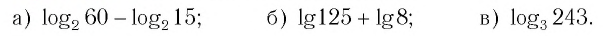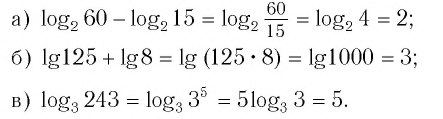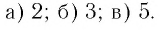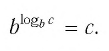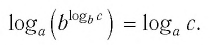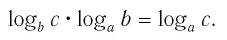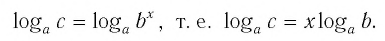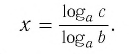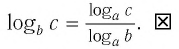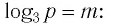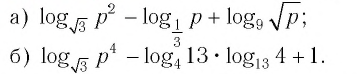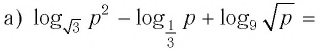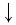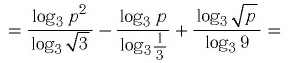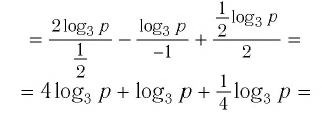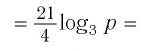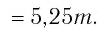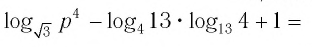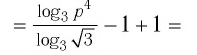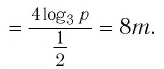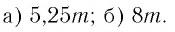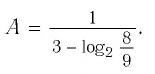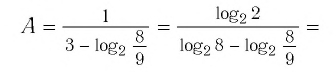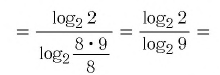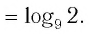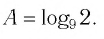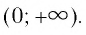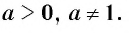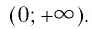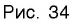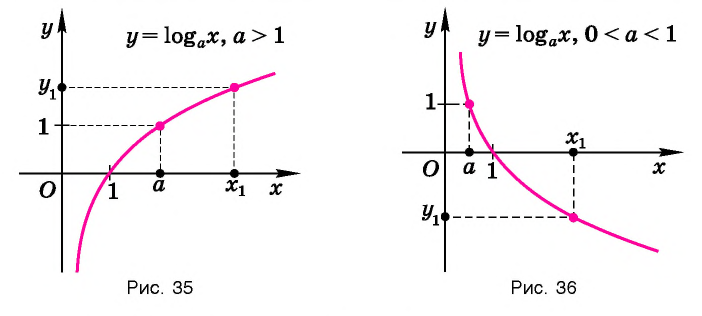что значит прологарифмировать выражение
Примеры решения задач с логарифмами
Логарифмы (Логарифмирование) активно используются в решении задач, так как значительно упрощают обычные алгебраические операции. Использование логарифмов позволяет заменить умножение на значительно более простое сложение, деление — на вычитание, а возведение в степень и извлечение корня заменяются соответственно на умножение и деление на показатель степени числа.
Перед изучением примеров решения задач советуем изучить теоретический материал по логарифмам, прочитать определения и все свойства логарифмов.
Логарифм произведения, сумма логарифмов
Примеры решения задач с логарифмами не по зубам? Тебе ответит эксперт через 10 минут!
Логарифм частного, разность логарифмов
Логарифм степени
Решение.$\log _ <2>\frac<1><8>+\log _ <5>25=\log _ <2>2^<-3>+\log _ <5>5^<2>=-3 \cdot \log _ <2>2+2 \cdot \log _ <5>5=$
Логарифм корня
$$=\log _ <8>4+\log _ <8>2=\log _<8>(4 \cdot 2)=\log _ <8>8=1$$
Разложение в ряд Маклорена натурального логарифма
Делая обратную замену, получаем:
$x^<2>+4=8 \Rightarrow x^<2>-4=0 \Rightarrow(x-2)(x+2) \Rightarrow x_<1>=2, x_<2>=-2$
Решение. ОДЗ:
$$\left\<\begin
$$x^<2>=x+2 \Rightarrow x^<2>-x-2=0 \Rightarrow x_<1>=2, x_<2>=-1$$
Решение. Находим ОДЗ:
$$\left\<\begin
Решение логарифмических неравенств
Решение. ОДЗ:
$$x-1>0 \Rightarrow x>1 \Rightarrow x \in(1 ;+\infty)$$
Учитывая выше написанное, получаем, что заданное логарифмическое неравенство равносильно неравенству:
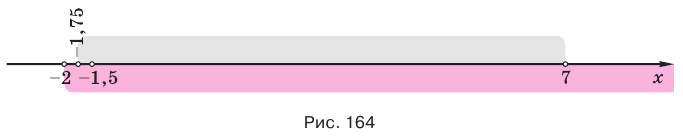
Решение. Данное неравенство равносильно системе:
Логарифмические выражения с примерами решения
Мы уже умеем по значению
Пример:
Решим уравнение 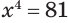
Теперь поставим задачу нахождения показателя 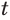
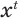
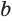
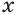
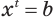
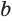
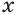
Пример:
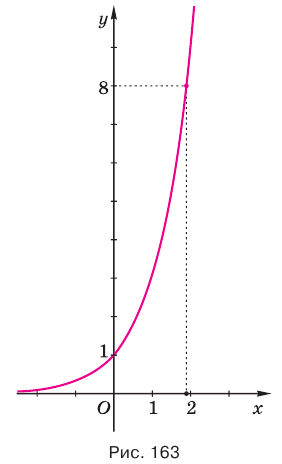
Решим уравнение 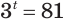
Это уравнение можно записать как 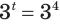
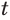
Обратим внимание на то, что при решении уравнения 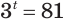
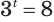
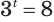
Этот корень называют логарифмом числа 8 по основанию 3 и обозначают 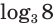
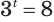
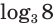
Логарифмом числа 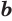
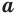
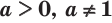
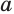
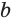
Логарифм числа 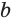
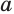
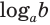
Пример:
Таким образом, учитывая определение логарифма числа, корень уравнения 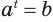
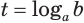
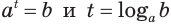
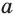
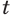
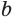
Пример:
Решим уравнение 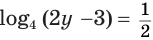
Определение логарифма позволяет данное уравнение заменить равносильным уравнением 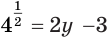
Определение логарифма коротко можно представить равенством
которое называют основным логарифмическим тождеством.
Пример:
Вычислим значение выражения 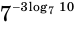
Используем свойство возведения степени в степень и основное логарифмическое тождество:
Из свойств показательной функции следует, что выражение 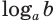
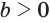
Пример:
Найдем область определения выражения
Данное выражение имеет значение, если основание логарифма 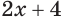
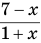
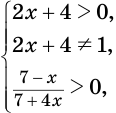
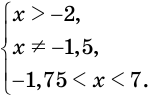
Из определения логарифма следует, что
Действие нахождения логарифма числа называется логарифмированием.
Введение действия логарифмирования порождает новый класс логарифмических выражений, т. е. выражений, которые содержат по крайней мере одно действие нахождения логарифма из выражения с переменной. При преобразованиях логарифмических выражений используются свойства действия логарифмирования. Установим эти свойства.
Теорема 5.
При любом положительном и не равном единице основании:
логарифм произведения положительных множителей равен сумме их логарифмов:
логарифм частного с положительными делимым и делителем равен разности логарифмов делимого и делителя:
логарифм любой действительной степени положительного числа равен произведению показателя степени и логарифма основания:
Доказательство:
Пусть 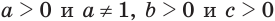
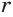
Основное логарифмическое тождество позволяет записать равенства:
Перемножив их, получим:
откуда, по определению логарифма:
Если разделить первое равенство из (1) на второе, то получим, что
откуда, по определению логарифма:
Возведя первое равенство из (1) в степень с показателем 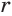
откуда, по определению логарифма:
Обращаем внимание на то, что при применениях тождеств, установленных теоремой 5, нужно следить за тем, чтобы все подлогарифмические выражения были положительными.
Пример:
а) 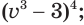
а) Получим
б) Выражение 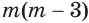
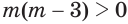
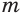
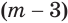
Если оба множителя 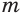
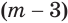
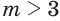
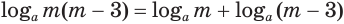
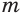
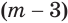
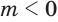
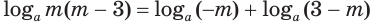
Действие, обратное логарифмированию, называют потенцированием.
Пример:
Пропотенцируем выражение 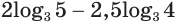
Будем последовательно получать:
Логарифмы чисел находят с помощью специальных таблиц или калькулятора. И в том, и в другом случае находят десятичные или натуральные логарифмы.
Десятичным логарифмом числа называют логарифм этого числа по основанию 10.
Для десятичного логарифма вместо 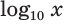
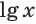
Для натурального логарифма вместо 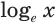
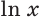
Для вычислений достаточно иметь возможность находить логарифмы по одному основанию, так как тогда можно найти логарифм числа по другому основанию. Это позволяет делать формула перехода к другому основанию.
Теорема 6.
Логарифм числа по данному основанию равен логарифму числа по новому основанию, деленному на логарифм данного основания по новому основанию:
Доказательство:
Пусть 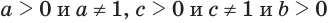
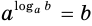
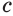
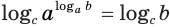
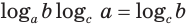
Пример:
Найдем, через сколько лет удвоится пятипроцентный вклад в банк.
Пусть имеется вклад в 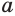
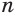
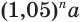
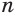
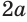
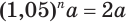
Вычисления проведем с помощью калькулятора, на котором есть клавиша для нахождения десятичных логарифмов:
Таким образом, удвоение пятипроцентного вклада произойдет через 14,2 года.
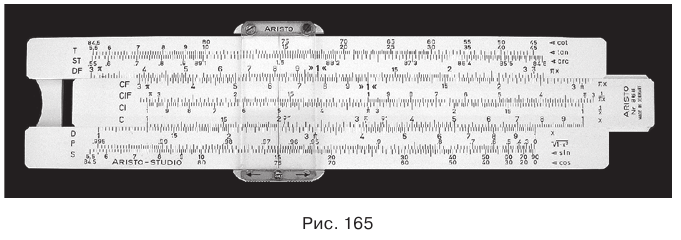
Открытие логарифмов было вызвано в XVI в. быстрым развитием астрономии и усложнением астрономических вычислений, которые имели непосредственное практическое значение при определении местонахождения судов по Солнцу и другим звездам. Логарифмы быстро вошли в практику.
Первые логарифмические таблицы были составлены в одно время и независимо друг от друга шотландским математиком Джоном Непером (1550—1617) и швейцарским математиком и астрономом Йобстом Бюрги (1552—1632). В 1623 г. английский математик Эдмунд Гантер изобрел логарифмическую линейку, с помощью которой действия над числами — умножение, деление — заменяются действиями сложения и вычитания над логарифмами этих чисел. На рисунке 165 показана одна из логарифмических линеек. Сейчас нужные вычисления проводятся с помощью калькуляторов. Леонард Эйлер (1707—1783) установил, что действие логарифмирования является обратным действию возведения в степень. Термин логарифм предложен Джоном Непером. Современное определение логарифма впервые дано в 1742 г. английским математиком Вильямом Гардинером.
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Метод логарифмирования
Один из методов решения уравнений – это метод логарифмирования. Сейчас мы детально разберем его с теоретической и практической стороны. Сначала покажем, когда применяется метод логарифмирования. Дальше дадим суть метода логарифмирования. После этого перейдем к теоретическому обоснованию. Затем запишем алгоритм решения уравнений методом логарифмирования. Наконец, рассмотрим примеры применения метода при решении уравнений.
Когда применяется
Метод логарифмирования обычно применяется для решения уравнений, логарифмирование обеих частей которых позволяет избавиться от переменной в показателях степеней. Если привязываться к внешнему виду, то такими, в основном, являются:
Суть метода логарифмирования
Суть метода логарифмирования состоит в логарифмировании обеих частей уравнения по одному и тому же основанию.
Это объясняет название метода.
Обоснование метода
В основе метода логарифмирования лежит следующая теорема:
Алгоритм решения уравнений методом логарифмирования
Информация из предыдущих пунктов позволяет записать алгоритм решения уравнений методом логарифмирования.
Чтобы решить уравнение методом логарифмирования, надо
Примеры применения
Осталось посмотреть, как метод логарифмирования применяется на практике. Для этого обратимся к конкретным примерам.
Решите уравнение 
Заданное уравнение представляет собой равенство двух степеней с положительными и отличными от единицы основаниями. Такие степени принимают только положительные значения, что следует из определения степени. Все это открывает дорогу для решения заданного уравнения методом логарифмирования.
Итак, все свелось к решению уравнения 

Все проделанные преобразования являются равносильными преобразованиями, поэтому, полученное уравнение равносильно уравнению, которое было до проведения этих преобразований. Полученное уравнение 
Остается сослаться на равносильность уравнения 


При решении следующего уравнения покажем, как правильно проводить логарифмирование по основанию с переменной.
Содержание:
Множеством (областью) значений показательной функции
Такое значение аргумента единственное, так как если 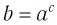
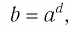
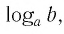
Таким образом, равенство 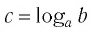
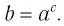
Определение:
Пусть 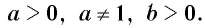
Приведем несколько примеров:
Нахождение логарифма числа называется логарифмированием.
Обозначим 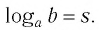
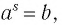
Это равенство называется основным логарифмическим тождеством.
Согласно этому тождеству, например, имеем: 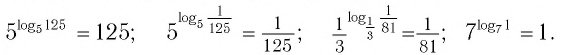
Например:
История логарифма
Логарифмы были изобретены в 1614 г. шотландским математиком Д. Непером (1550—1617) и независимо от него на 6 лет позднее швейцарским механиком и математиком И. Бюрги (1552—1632).
Оба исследователя хотели найти новое удобное средство арифметических вычислений, но их определения логарифма различны и у обоих не похожи на современные. Понимание логарифма как показателя степени с данным основанием впервые появилось в XVIII в. в работах английского математика В. Гардинера (1742). Широкому распространению этого определения логарифма более других содействовал Jl. Эйлер, который впервые применил в этой связи и термин «основание».
Термин «логарифм» принадлежит Неперу. Он возник из сочетания греческих слов логос — отношение и аритмос — число. Слово «логарифм», таким образом, означало «число отношения».
Пример:
а) Записать число 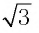
Решение:
а) По определению логарифма имеем:
б) По определению логарифма имеем:
Пример:
Между какими целыми числами находится число
Решение:
Пусть 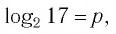
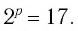
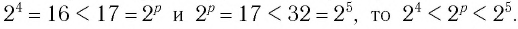
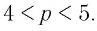
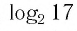
Ответ:
Пример:
Решение:
а) Поскольку 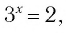
б)
Ответ:
Логарифмы по основанию 10 имеют особое название — десятичные логарифмы. Десятичный логарифм числа b обозначается 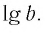
▲ Особое обозначение и название имеют не только десятичные логарифмы, но и логарифмы, основанием которых является число е:
Такие логарифмы называются натуральными.
Логарифмы по основанию е позволяют выражать математическую зависимость, которая характеризует многие биологические, химические, физические, социальные и другие процессы. По-видимому, этим объясняется и название «натуральные логарифмы», т. е. естественные (этот термин ввел в 1659 г. итальянский математик П. Менголи). Натуральные и десятичные логарифмы имели большое значение для облегчения вычислений в XVII—XX вв. до создания мощных современных вычислительных средств. Натуральные логарифмы имеют и большое теоретическое значение.▲
Основные свойства логарифмов
Теорема:
При любых положительных значениях b и с верно равенство:
Докажем утверждение (1).
По основному логарифмическому тождеству
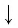
Таким образом, имеем:
Отсюда по следствию из п. 2.3 получаем равенство (1).
Докажем утверждение (2). Преобразуем левую часть равенства (2):
Заметим, что равенство (2) можно доказать тем же способом, что и равенство (1), — сделайте это самостоятельно.
Равенство (1) означает, что логарифм произведения двух положительных чисел равен сумме логарифмов этих чисел.
Равенство (2) означает, что логарифм дроби с положительными. числителем и знаменателем равен разности логарифмов числителя и знаменателя.
Замечание. Равенства, доказанные в теореме 1 (как и другие равенства этого пункта), являются тождествами. Действительно, каждое из них превращается в верное числовое равенство при любых значениях a, b и с, для которых входящие в равенство выражения имеют смысл.
Теорема:
При любых значениях s и положительных значениях b верно равенство
По основному логарифмическому тождеству
Таким образом, имеем
Отсюда по следствию из п. 2.3 получаем равенство (3).
Следствие 1. Если числа 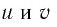
Следствие 2. При любом целом 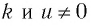
Пример №1
Найти значение выражения:
Решение:
Ответ:
Теорема:
При любых значениях 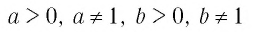
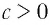
Способ 1. По основному логарифмическому тождеству имеем
Прологарифмировав левую и правую части этого тождества по основанию а, получим
Применив тождество (3), имеем
Так как 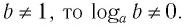
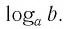
Способ 2. Пусть 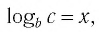
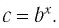
Итак,
Тождество (6) называется формулой перехода от логарифма по одному основанию к логарифму по другому основанию.
Обычно в таблицах, калькуляторах даются значения логарифмов по основанию 10, а когда нужно найти значение логарифма по другому основанию, пользуются формулой перехода от логарифма по одному основанию к логарифму по другому основанию.
Следствием из тождества (6) при основании а = с является формула
(убедитесь в этом самостоятельно).
Пример №2
Найти значение выражения, если
Решение:




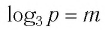
6)


Ответ:
Следствие 3. Имеют место тождества:
Тождества (8) и (9) можно доказать, используя уже доказанные тождества из этого пункта.
Пример №3
Упростить выражение
Решение:
Используя определение логарифма, представим числа 1 и 3 в виде логарифмов по основанию 2:
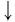
Ответ:
Развитие науки, прежде всего астрономии, уже в XVI в. привело к необходимости громоздких вычислений при умножении и делении многозначных чисел. Эти вычислительные проблемы были в некоторой степени решены с открытием логарифмов и созданием таблиц логарифмов.
Логарифмическая функция
Рассмотрим выражение 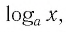
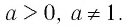
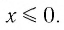
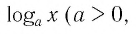
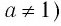
Определение:
Логарифмической функцией называется функция вида 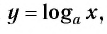
Область определения логарифмической функции — это естественная область определения выражения 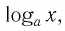
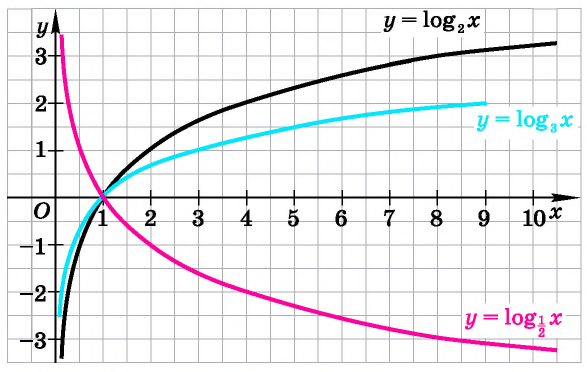
Графики некоторых логарифмических функций изображены на рисунке 34. Эти изображения (как и для графиков других функций) можно было получить, строя их по точкам. Отметим некоторые особенности изображенных графиков.
График функции 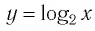
Когда значения аргумента х уменьшаются, т. е. приближаются к нулю, то график этой функции «приближается» к оси Оу и при этом «круто» опускается вниз. А когда значения аргумента х увеличиваются, то график «медленно» поднимается вверх (ем. рис. 34). Аналогично для любой функции 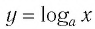
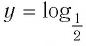
Заметим, что когда значения аргумента х уменьшаются, т. е. приближаются к нулю, то график этой функции «приближается» к оси Оу и при этом «круто» поднимается вверх. А когда значения аргумента х увеличиваются, то график «медленно» опускается вниз. Аналогично для любой функции 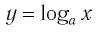
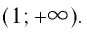
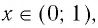
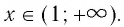
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.