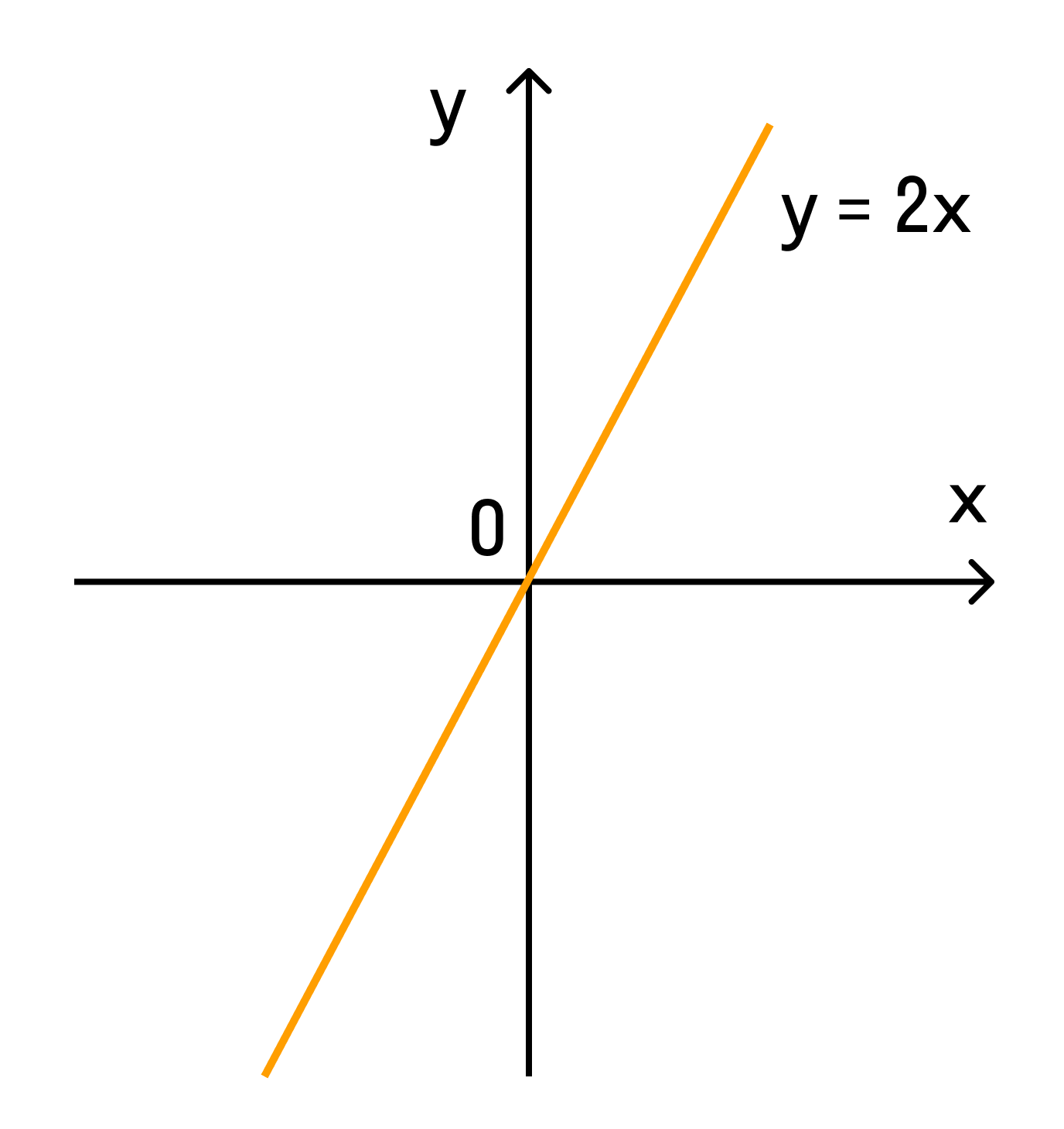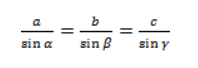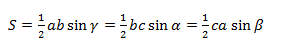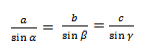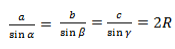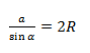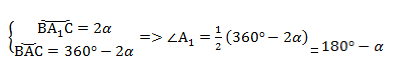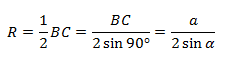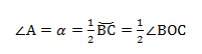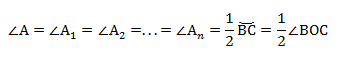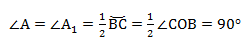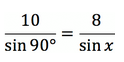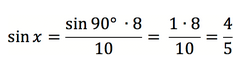что значит пропорциональные углы

Прямая и обратная пропорциональность

Основные определения

Математическая зависимость — это соответствие между элементами двух множеств, при котором каждому элементу одного множества ставится в соответствие элемент из другого множества.

Зависимости также можно классифицировать по формам: функциональная и статистическая.

Функциональная зависимость между двумя переменными величинами характеризуется тем, что каждому значению одной из них соответствует вполне определенное и единственное значение другой.

В математике функциональной зависимостью переменной Y от переменной Х называют зависимость вида y = f(x), где каждому допустимому значению X ставится в соответствие по определенному правилу единственно возможное значение Y.

Статистическая зависимость — это зависимость случайных величин, когда изменение одной переменной приводит к изменению другой.

Если изменение одной из случайных величин влечет изменение среднего другой случайной величины, то статистическую зависимость называют корреляционной. Сами случайные величины, связанные корреляционной зависимостью, оказываются коррелированными.

Пропорция в математике — это равенство между отношениями двух или нескольких пар чисел или величин. Пропорциональными называются две взаимно-зависимые величины, если отношение их значений остается неизменным.

Пропорциональность — это взаимосвязь между двумя величинами, при которой изменение одной из них влечет за собой изменение другой во столько же раз. Проще говоря — это зависимость одного числа от другого.

Есть две разновидности пропорциональностей:

Коэффициент пропорциональности — это неизменное отношение пропорциональных величин. Он показывает, сколько единиц одной величины приходится на единицу другой. Коэффициент пропорциональности обозначается латинской буквой k.

Прямо пропорциональные величины

Две величины называются прямо пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая увеличивается (или уменьшается) во столько же раз.

Прямая пропорциональность в виде схемы: «больше — больше» или «меньше — меньше».

Свойство прямо пропорциональной зависимости:

Если две величины прямо пропорциональны, то отношения соответствующих значений этих величин равны.

Примеры прямо пропорциональной зависимости:

Если говорить метафорами, то прямую пропорциональную зависимость можно отличить от обратной по пословице: «Чем дальше в лес, тем больше дров». Что значит, чем дольше ты идешь по лесу, тем больше дров можно собрать.

Формула прямой пропорциональности

y = kx,

где y и x — переменные величины, k — постоянная величина, которую называют коэффициентом прямой пропорциональности.

Коэффициент прямой пропорциональности — это отношение любых соответствующих значений пропорциональных переменных y и x, равное одному и тому же числу.

Формула коэффициента прямой пропорциональности:

Графиком прямо пропорциональной зависимости величин является прямая линия.

Например, при k = 2 график выглядит так:

Пример 1.

В одно и то же путешествие поехали два автомобиля. Один двигался со скоростью 70 км/ч и за 2 часа проделал тот же путь, что другой за 7 часов. Найти скорость второго автомобиля.

Пример 2.

Блогер за 8 дней может написать 14 постов. Сколько помощников ему понадобится, чтобы написать 420 постов за 12 дней?

Количество человек (блогер и помощники) увеличивается с увеличением объема работы, если ее нужно сделать за то же количество времени.

Если разделить 420 на 14, узнаем, что объем увеличивается в 30 раз.

Но так как по условию задачи на работу дается больше времени, то количество помощников увеличивается не в 30 раз. Таким образом:

Ответ: 20 человек напишут 420 постов за 12 дней.

Обратно пропорциональные величины

Две величины называют обратно пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая уменьшается (или увеличивается) во столько же раз.

Объясним, что значит обратно пропорционально в виде схемы: «больше — меньше» или «меньше — больше».

Свойство обратной пропорциональности величин:

Если две величины находятся в обратно пропорциональной зависимости, то отношение двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины.

Примеры обратно пропорциональной зависимости:

Формула обратной пропорциональности

где y и x — это переменные величины,

k — постоянная величина, которую называют коэффициентом обратной пропорциональности.

Коэффициент обратной пропорциональности — это произведение любых соответствующих значений обратно пропорциональных переменных y и x, равное одному и тому же числу.

Формула коэффициента обратной пропорциональности:

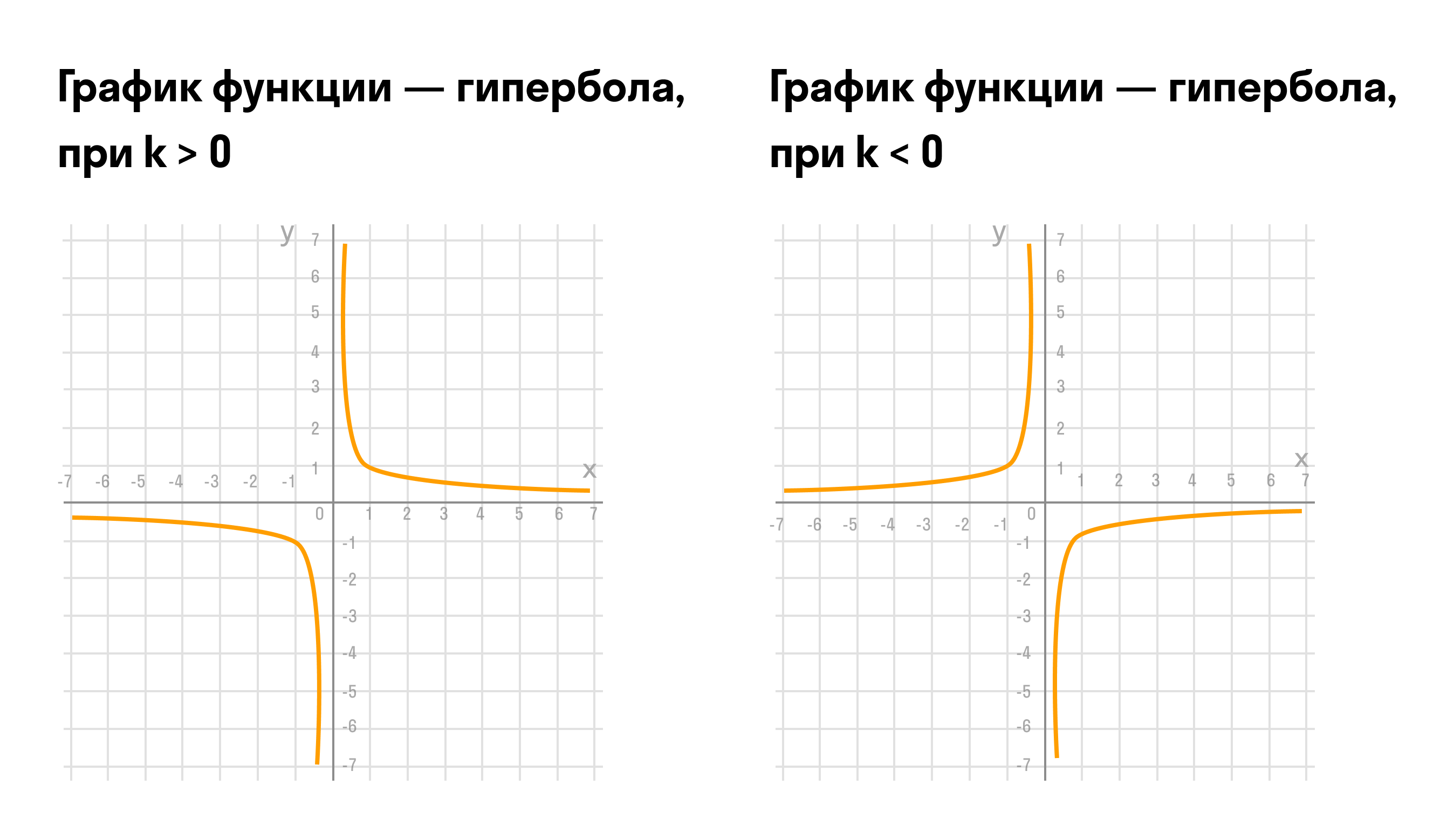
Графиком обратно пропорциональной зависимости величин является гипербола.

Свойства функции обратной пропорциональности:

Потренируемся

Пример 1. 24 человека за 5 дней раскрутили канальчик в ютубе. За сколько дней выполнят ту же работу 30 человек, если будут работать с той же эффективностью?

Пример 2. Автомобиль проезжает от одного города до другого за 13 часов со скоростью 75 км/ч. Сколько времени ему понадобится, если он будет ехать со скоростью 52 км/ч?

Скорость и время связаны обратно пропорциональной зависимостью: чем больше скорость, тем меньше времени понадобится.

Соотношения равны, но перевернуты относительно друг друга.

Источник

Теорема синусов

Доказательство теоремы синусов

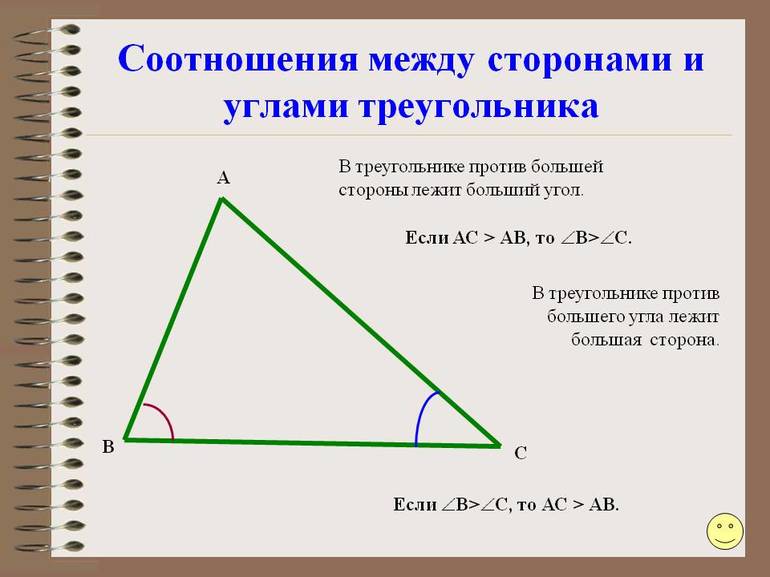
Теорема синусов звучит так: стороны треугольника пропорциональны синусам противолежащих углов.

Нарисуем стандартный треугольник и запишем теорему формулой:

Формула теоремы синусов:

Докажем теорему с помощью формулы площади треугольника через синус его угла.

Из этой формулы мы получаем два соотношения:

Из этих двух соотношений получаем:

Теорема синусов для треугольника доказана.

Эта теорема пригодится, чтобы найти:

Доказательство следствия из теоремы синусов

У теоремы синусов есть важное следствие. Нарисуем треугольник, опишем вокруг него окружность и рассмотрим следствие через радиус.

где R — радиус описанной около треугольника окружности.

Так образовались три формулы радиуса описанной окружности:

Основной смысл следствия из теоремы синусов заключен в этой формуле:

Радиус описанной окружности не зависит от углов α, β, γ. Удвоенный радиус описанной окружности равен отношению стороны треугольника к синусу противолежащего угла.

Для доказательства следствия теоремы синусов рассмотрим три случая.

1. Угол ∠А = α — острый в треугольнике АВС.

Проведем диаметр BA1. В этом случае точка А и точка А1 лежат в одной полуплоскости от прямой ВС.

Используем теорему о вписанном угле и видим, что ∠А = ∠А1 = α. Треугольник BA1C — прямоугольный, в нём ∠ BCA1 = 90°, так как он опирается на диаметр BA1.

Чтобы найти катет a в треугольнике BA1C, нужно умножить гипотенузу BA1 на синус противолежащего угла.

BA1 = 2R, где R — радиус окружности

Следовательно: R = α/2 sinα

Для острого треугольника с описанной окружностью теорема доказана.

2. Угол ∠А = α — тупой в треугольнике АВС.

Проведем диаметр окружности BA1. Точки А и A1 по разные стороны от прямой ВС. Четырёхугольник ACA1B вписан в окружность, и его основное свойство в том, что сумма противолежащих углов равна 180°.

Вспомним свойство вписанного в окружность четырёхугольника:

В треугольнике BCA1 угол при вершине С равен 90°, потому что он опирается на диаметр. Следовательно, катет а мы находим таким образом:

Следовательно: R = α/2 sinα

Для тупого треугольника с описанной окружностью теорема доказана.

Часто используемые тупые углы:

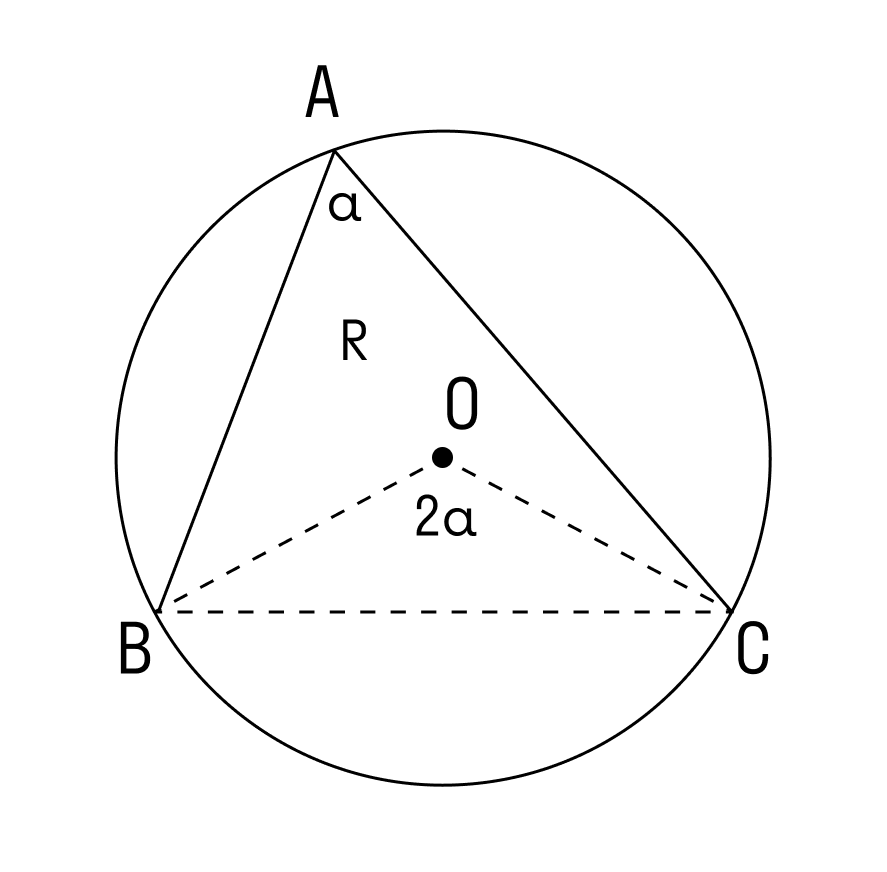
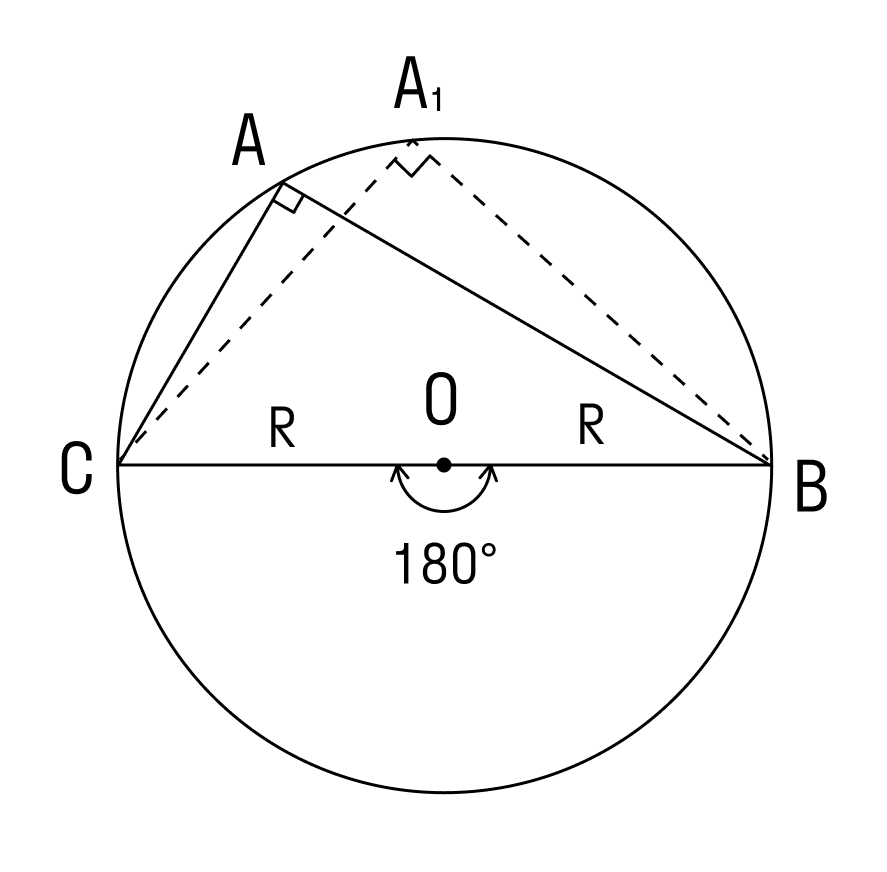
3. Угол ∠А = 90°.

В прямоугольнике АВС угол А прямой, а противоположная сторона BC = α = 2R, где R — это радиус описанной окружности.

Для прямоугольного треугольника с описанной окружностью теорема доказана.

Теорема о вписанном в окружность угле

Из теоремы синусов и ее следствия можно сделать любопытный вывод: если известна одна сторона треугольника и синус противолежащего угла — можно найти и радиус описанной окружности. Но треугольник не задаётся только этими величинами. Это значит, что если треугольник еще не задан, найти радиус описанной окружности возможно.

Раскроем эту тему на примере теоремы о вписанном в окружность угле и следствиях из нее.

Теорема о вписанном угле: вписанный в окружность угол измеряется половиной дуги, на которую он опирается.

∠А = α опирается на дугу ВС. Дуга ВС содержит столько же градусов, сколько ее центральный угол ∠BOC.

Формула теоремы о вписанном угле:

Следствие 1 из теоремы о вписанном в окружность угле

Вписанные углы, опирающиеся на одну дугу, равны.

∠А = ∠BAC опирается на дугу ВС. Поэтому ∠A = 1/2(∠COB).

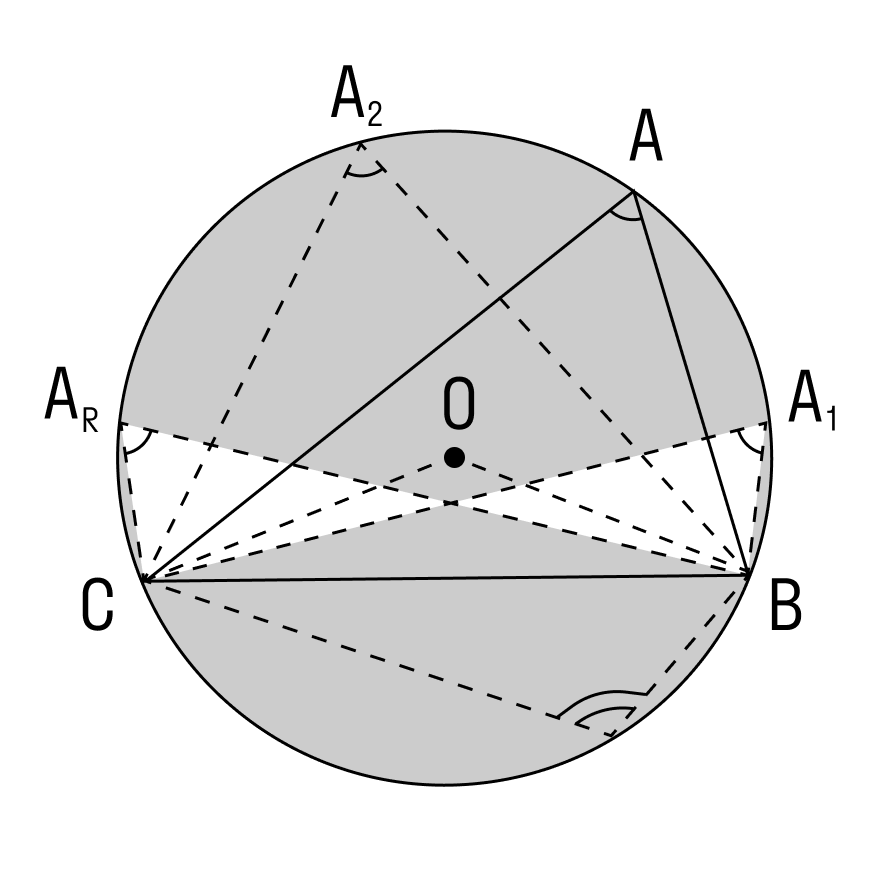
Если мы возьмём точки A1, А2. Аn и проведём от них лучи, которые опираются на одну и ту же дугу, то получим:

На рисунке изображено множество треугольников, у которых есть общая сторона СВ и одинаковый противолежащий угол. Треугольники являются подобными, и их объединяет одинаковый радиус описанной окружности.

Следствие 2 из теоремы о вписанном в окружность угле

Вписанные углы, которые опираются на диаметр, равны 90°, то есть прямые.

ВС — диаметр описанной окружности, следовательно ∠COB = 180°.

Следствие 3 из теоремы о вписанном в окружность угле

Сумма противоположных углов вписанного в окружность четырёхугольника равна 180°. Это значит, что:

Угол ∠А = α опирается на дугу DCB. Поэтому DCB = 2α по теореме о вписанном угле.

Угол ∠С = γ опирается на дугу DAB. Поэтому DAB = 2γ.

Но так как 2α и 2γ — это вся окружность, то 2α + 2γ = 360°.

Следовательно: α + γ = 180°.

Следствие 4 из теоремы о вписанном в окружность угле

Синусы противоположных углов вписанного четырехугольника равны. То есть:

Примеры решения задач

Теорема синусов и следствия из неё активно используются при решении задач. Рассмотрим несколько примеров, чтобы закрепить материал.

Пример 1. В треугольнике ABC ∠A = 45°,∠C = 15°, BC = 4√6. Найти AC.

Пример 2. Гипотенуза и один из катетов прямоугольного треугольника равны 10 и 8 см. Найти угол, который расположен напротив данного катета.

В этой статье мы узнали, что в прямоугольном треугольнике напротив гипотенузы располагается угол, равный 90°. Примем неизвестный угол за x. Тогда соотношение сторон выглядит так:

Значит x = sin (4/5) ≈ 53,1°.

Ответ: угол составляет примерно 53,1°.

Запоминаем

Обычная теорема: стороны треугольника пропорциональны синусам противолежащих углов.

>

Расширенная теорема: в произвольном треугольнике справедливо следующее соотношение:

Источник

Что значит пропорциональные углы

Признака подобия треугольников

Две фигуры `F` и `F’` называются подобными, если они переводятся друг в друга преобразованием подобия, т. е. таким преобразованием, при котором расстояния между точками изменяются (увеличиваются или уменьшаются) в одно и то же число раз. Если фигуры `F` и `F’` подобны, то пишется `F

F’`. Напомним, что запись подобия треугольников `Delta ABC

Из свойств преобразования подобия следует, что у подобных фигур соответствующие углы равны, а соответствующие отрезки пропорциональны. В частности, если `Delta ABC

Delta A_1B_1C_1`, то `/_ A = /_ A_1`, `/_ B = /_ B_1`, `/_ C = /_ C_1`,

`A_1B_1 : AB = B_1C_1 : BC = C_1A_1 : CA`.

Два треугольника подобны, если:

1. два угла одного соответственно равны двум углам другого;

2. две стороны одного пропорциональны двум сторонам другого и углы, образованные этими сторонами, равны;

3. три стороны одного треугольника пропорциональны трём сторонам другого.

В решении задач и доказательстве теорем часто используется утверждение, которое, чтобы не повторять каждый раз, докажем сейчас отдельно.

Если две стороны треугольника пересекает прямая, параллельная третьей стороне (рис. 9), то она отсекает треугольник, подобный данному.

Действительно, из параллельности `MN` и `AC` следует, что углы `1` и `2` равны. Треугольники `ABC` и `MBN` имеют два равных угла: общий угол при вершине `B` и равные углы `1` и `2`. По первому признаку эти треугольники подобны.

И сразу применим это утверждение в следующем примере, в котором устанавливается важное свойство трапеции.

Прямая, проходящая через точку пересечения диагоналей трапеции параллельно её основаниям, пересекает боковые стороны трапеции в точках `M` и `N`. Найти длину отрезка `MN`, если основания трапеции равны `a` и `b`.

Delta COB` по двум углам (рис. 10б):

`(OD)/(OB) = (AD)/(BC)`, то есть `(OD)/(OB) = a/b`.

3. Учитывая, что `BD = BO + OD` находим отношение

`(BO)/(BD) = (BO)/(BO + OD) = 1/(1 + OD//BO) = b/(a + b)`.

Подставляя это в (1), получаем `MO = (ab)/(a + b)`; аналогично устанавливаем, что `ON = (ab)/(a + b)`, таким образом `MN = (2ab)/(a + b)`.

Delta MBF`. Из подобия следует `(AE)/(MF) = (AM)/(MB) = 1/3`.

Напомним, что отношение периметров подобных треугольников равно отношению их сходственных сторон. Верно также следующее утверждение: отношение медиан, биссектрис и высот, проведённых к сходственным сторонам в подобных треугольниках, равно отношению сходственных сторон.

Отношение радиусов вписанных окружностей, как и отношение радиусов описанных окружностей, в подобных треугольниках также равно отношению сходственных сторон.

Попытайтесь доказать это самостоятельно.

Прямоугольные треугольники подобны, если:

1. они имеют по равному острому углу;

2. катеты одного треугольника пропорциональны катетам другого;

3. гипотенуза и катет одного треугольника пропорциональны гипотенузе и катету другого.

Два первых признака следуют из первого и второго признаков подобия треугольников, поскольку прямые углы равны. Третий признак следует, например, из второго признака подобия и теоремы Пифагора.

Заметим, что высота прямоугольного треугольника, опущенная на гипотенузу, разбивает его на два прямоугольных треугольника, подобных между собой и подобных данному. Доказанные в § 1 метрические соотношения Свойств 1, 2, 3 можно доказать, используя подобие указанных треугольников.

СВОЙСТВА ВЫСОТ И БИССЕКТРИС

Если в треугольнике `ABC` нет прямого угла, `A A_1` и `BB_1` — его высоты, то `Delta A_1B_1C

Delta ABC` (этот факт можно сформулировать так: если соединить основания двух высот, то образуется треугольник, подобный данному).

Как всегда, полагаем `AB = c`, `BC = a`, `AC = b`.
а) Треугольник `ABC` остроугольный (рис. 12а).

В треугольниках `A_1 B_1C` и `ABC` угол `C` общий, прилежащие стороны пропорциональны: `(A_1C)/(AC) = (B_1C)/(BC) = cos C`.

Таким образом, `Delta A_1 B_1 C

$$\left.\begin
\Delta AA_1C, \angle A_1 =90^\circ \Rightarrow A_1C=AC\cdot \cos C =b \cos C;\\
\Delta BB_1C, \angle B_1 =90^\circ \Rightarrow B_1C=BC\cdot \cos C =a \cos C,
\end
\right\>\Rightarrow \Delta A_1B_1C\sim \Delta ABC,$$

коэффициент подобия `ul (cos C)`, `/_ A_1 B_1 C = /_B`.

$$\left.\begin
\Delta AA_1C, \angle A_1 =90^\circ \Rightarrow A_1C=AC\cdot \cos\varphi =b |\cos C|;\\
\Delta BB_1C, \angle B_1 =90^\circ \Rightarrow B_1C=BC\cdot \cos\varphi =b |\cos C|,
\end
\right\>\Rightarrow \Delta A_1B_1C\sim \Delta ABC$$

с коэффициентом подобия `ul (k = |cos C|`, `(/_A_1B_1C=/_B)`.

В остроугольном треугольнике `ABC` проведены высоты `A A_1`, `B B_1`, `C C_1` (рис. 13).

Треугольник, вершинами которого служат основания высот, называется «высотным» треугольником (или ортотреугольником).

Доказать, что лучи `A_1 A`, `B_1 B` и `C_1 C` являются биссектрисами углов высотного треугольника `A_1 B_1 C_1` (т. е. высоты остроугольного треугольника являются биссектрисами ортотреугольника).

По первой лемме о высотах `Delta A_1 B_1 C

Delta ABC`, `/_ A_1 B_1 C = /_ B`.

Аналогично `Delta AB_1C_1

Delta ABC`, `/_ AB_1 C_1 = /_ B`, т. е. `/_A_1 B_1C = /_ AB_1 C_1`.

Высоты `A A_1`, `B B_1` треугольника `ABC` пересекаются в точке `H` (рис. 14). Доказать, что имеет место равенство `AH * H A_1 = BH * HB_1`, т. е. произведение отрезков одной высоты равно произведению отрезков другой высоты.

Delta BHA_1`, имеют по равному острому углу при вершине `H` (заметим, что этот угол равен углу `C`). Из подобия следует `(AH)/(BH) = (HB_1)/(HA_1)`, откуда `AH * HA_1 = BH * HB_1`. Для тупоугольного треугольника утверждение также верно. Попробуйте доказать самостоятельно.

Высоты `A A_1` и `B B_1` треугольника `ABC` пересекаются в точке `H`, при этом `BH = HB_1` и `AH = 2 HA_1` (рис. 15). Найти величину угла `C`.

Установим ещё одно свойство биссектрисы угла треугольника.

Биссектриса треугольника делит одну из сторон треугольника на отрезки длиной `3` и `5`. Найти в каких пределах может изменяться периметр треугольника.

По свойству биссектрисы `AB : AC = 3:5`. Положим `AB = 3x`, тогда `AC = 5x`. Каждая сторона треугольника должна быть меньше суммы двух других сторон, т. е. `ul (5x 1`.

Периметр треугольника `P = 8 + 8x = 8(1 + x)`, поэтому `ul (16

Источник

О многоугольнике с тремя сторонами

Соотношение углов и сторон в треугольнике интуитивно можно понять, если хорошо представлять эту фигуру. Речь идет о плоском объекте, который состоит всего из трех отрезков. Они расположены таким образом, что начало первого совпадает с концом последнего, то есть они пересекаются. Каждый отрезок представляет собой независимую сторону фигуры. Точка пересечения является вершиной, а соответствующий ей угол является внутренним.

Таким образом, два ключевых элемента образуют рассматриваемую фигуру:

И вершин, и сторон в любом треугольнике по три, поэтому его принято обозначать большими латинскими буквами, например, ABC или MNK. Малые буквы резервируют для обозначения длин сторон, например, a, b, c.

На первый взгляд может показаться, что рассматриваемый объект является несложным, и в нем нечего изучать. Действительно, он является самым простым по построению многоугольником, однако, он обладает большим количеством свойств, количественное и качественное знание которых требуют понимания многих теорем.

Существование фигуры

Пусть имеется три отрезка, и необходимо понять, возможно ли из них построить треугольник. Это можно сделать с помощью одного простого правила, которое можно сформулировать следующим образом: любая сторона треугольника всегда меньше суммы длин двух других.

Знание этого правила является очень важным и эффективным инструментом при решении задач. Например, из отрезков с условными длинами 1, 2 и 4 построить треугольник невозможно, а из 2, 3, 4 это сделать можно.

Помимо соотношения длин сторон существует также еще одна теорема, которая гласит, что во всяком треугольнике сумма его внутренних углов всегда равна 180 °. Благодаря знанию этой теоремы можно все рассматриваемые фигуры разделить на три типа:

Полноты ради следует сказать о вырожденных фигурах. К ним относятся такие многоугольники, у которых тупой стремится к 180 °. Несложно представить, что в этом случае два других будут обращаться в ноль, а сумма противолежащих им сторон окажется равной длине отрезка, расположенного напротив тупого угла. На плоскости вырожденный треугольник представляет отрезок, его площадь стремится к нулю.

Важные линии

Несмотря на всю простоту построения треугольника, при решении задач могут понадобиться дополнительные отрезки. Внутри фигуры существует целая гамма типов этих отрезков, наиболее важными из них являются следующие:

Для правильных, равнобедренных и прямоугольных треугольников некоторые из названных отрезков могут совпадать друг с другом, а также со сторонами фигуры. Например, в прямоугольном треугольнике две малые стороны (катеты) также являются высотами.

Соотношение отрезков и углов

Задачи на соотношение отрезков и угловых мер в рассматриваемой фигуре могут требовать либо качественный, либо количественный ответ. В первом случае следует провести определенное доказательство, опираясь на известные аксиомы и теоремы о сторонах треугольника и их следствия. Во втором же случае следует пользоваться формулами и выражениями, которые содержат тригонометрические функции. В действительности оба типа задач связаны между собой. Так, прежде чем использовать какую-либо формулу, следует доказать возможность ее применения в конкретной ситуации.

Большие и меньшие длины

Основная теорема о соотношении между элементами в рассматриваемом типе многоугольников гласит, что против большего угла лежит большая сторона. Ее доказательство провести несложно, если построить треугольник, например, тупоугольный. Из тупого провести отрезок к противоположной стороне таким образом, чтобы он образовывал новый равнобедренный треугольник внутри исходного. После этого следует воспользоваться тем свойством, что внешний угол треугольника всегда больше внутреннего.

Следуя условию равенства углов в построенном равнобедренном треугольнике, легко показать, что против тупого всегда находится самый длинный отрезок.

Обратно эта теорема также справедлива, то есть против большей стороны треугольника лежит больший угол. Ее справедливость понятна каждому школьнику на интуитивном уровне, а доказательство заключается в переборе возможных трех вариантов соотношения между отрезками (больше, меньше, равно) и в привлечении уже доказанной теоремы.

Рассмотренные теоремы приводят к двум важным следствиям:

Рассмотренные теоремы и их следствия активно используются при изучении подобных фигур. Поскольку напротив равных углов двух треугольников лежат соответствующие им длины отрезков, то последние будут попарно относиться друг к другу с определенным коэффициентом подобия.

Теоремы косинусов и синусов

Количественной характеристикой соотношения сторон и углов являются знаменитые формулы, содержащие зависимость длин отрезков и угловых мер. Первая из них называется теоремой косинусов. Соответствующая формула имеет вид:

c 2 = a 2 + b 2 — 2*a*b*cos©.

Здесь величины a, b, c — это длины, C — угол напротив стороны c. Формула позволяет вычислить третью сторону по известным двум другим и углу между ними. Однако, возможности выражения шире, с его помощью можно посчитать всякий внутренний угол фигуры, если известны три ее стороны.

Следующая по счету, но не по важности теорема синусов. Ее математическое выражение записывается так:

a/sin (A) = b/sin (B) = c/sin©.

Эти равенства говорят о том, что отношение стороны к синусу противоположного ей угла является постоянной характеристикой конкретного треугольника. Зная связь двух углов и стороны или двух отрезков и одного угла можно рассчитать все остальные характеристики фигуры. Следует запомнить, что для любого рассматриваемого типа многоугольников однозначное вычисление всех его свойств требует знания минимум трех элементов (кроме трех углов).

Прямоугольный треугольник

Этот особый случай следует рассмотреть подробнее. Каждый школьник знает знаменитую теорему, позволяющую сравнить соответствие отрезков друг другу в этом типе фигуры. Она гласит, что сумма квадратов катетов соответствует квадрату гипотенузы, и называется пифагоровой теоремой, то есть можно записать:

Работать с прямоугольными треугольниками удобно по одной простой причине: через их геометрические параметры вводятся в математику тригонометрические функции. Последние легко использовать при вычислении сторон и углов фигуры. Например, если фигура является не только прямоугольной, но и равнобедренной, то ее катеты равны, а углы напротив них составляют по 45 °. При этом любой из катетов всегда в 2 0,5 раза меньше гипотенузы:

Это соотношение можно получить также из теоремы Пифагора.

Другая ситуация, когда один из острых углов равен 30 °. Для лежащего напротив него катета a можно записать следующее выражение:

Иными словами, лежащий против 30 ° катет составляет ровно половину длины гипотенузы.

Таким образом, в любом треугольнике существует прямая пропорциональность между длиной стороны и противолежащим ей углом. Для количественного решения задач по геометрии с этой фигурой следует пользоваться выражениями синусов, косинусов и теоремой Пифагора.

Источник

• ← что значит родина для некрасова
• что делать если собаку укусила уличная собака →