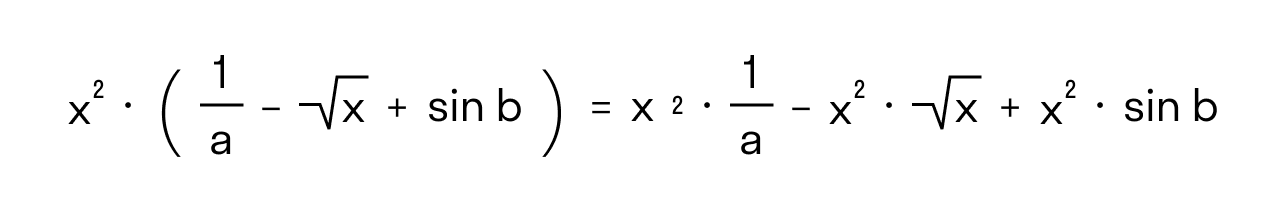что значит равно и скобка

Список текстовых смайлов и акронимов

Общался с молодым поколением, в ответ на мои текстовые смайлы пришел вопрос – «А это что значит?».
Решил написать, после первого десятка устал – решил, что проще найти в Интернете, нашел конечно но как-то кусками, тут несколько там несколько. Большинство из того, что нашлось были сайты с коллекциями графических смайлов. Из того, что нашел решил собрать коллекцию, чтобы потом больше не искать. Маленькое замечание по поводу использования, реально используется около 10% от представленного тут списка. С японскими еще сложнее, их используют в основном анимешники.

История создания:
Ещё в 1969 году Владимир Набоков в одном из своих интервью упоминал о том, что сто́ит создать специальный знак пунктуации для графического отображения эмоций:
«Мне часто приходит на ум, что надо придумать какой-нибудь типографический знак, обозначающий улыбку, — какую-нибудь закорючку или упавшую навзничь скобку, которой я бы мог сопроводить ответ на ваш вопрос.»
Однако Скотт Фалман (англ. Scott E. Fahlman) 19 сентября 1982 года первым в мире предложил смайлик в том виде, в котором он популярен сейчас, в переписке:
«Предлагаю использовать вот такую последовательность символов для обозначения шутливых сообщений: »
Установить точно, кто придумал смайлик, вряд ли возможно, так как есть свидетельства, что этот знак использовали ещё в 1960-х годах.

Японские (вертикальные) смайлы не нуждаются в напряжении шейных мышц (в этом плане они лучше для здоровья): в такой картинке

q(^_^)p можно сразу увидеть уши, изображенные символами q и p, лицо, ограниченное скобками, глаза и рот.

Японские смайлы:
Такой (^_^) вариант по японской канонике изображает мужчину, женщина рисуется так (^.^).

Изменяя количество подчеркиваний в предыдущем смайле, можно показать, что вашей радости просто нет границ! (^_____^).

(-_-)y-.o0O – Курильщик.

Далее приведен список не стандартных но забавных и необычных смайликов.

Что такое Акронимы?

Акронимы часто набирают кириллицей: ИМХО, лол, бб, гг и т. п.

Бытовые и житейские смайлы

Смайлы для Влюбленных

Разные смайлы

Разное

Mнoгo paзныx yлыбoк в coчeтaнияx oбpaзyют Cyпep-yлыбки

>:^#>) Уфф. Caми пepeвeдётe!

Источник

Раскрытие скобок

Понятие раскрытия скобок

В задачах по математике постоянно встречаются числовые и буквенные выражения, а также выражения с переменными, которые составлены с использованием скобок.

Основная функция скобок — менять порядок действий при вычислениях значений числовых выражений.

Часто можно перейти от одного выражения со скобками к тождественно равному выражению без скобок. Например:

Такой переход от выражения со скобками к тождественно равному выражению без скобок несет в себе основную идею о раскрытии скобок.

Начальное выражение со скобками и результат, полученный после раскрытия скобок, удобно записывать в виде равенства, как мы это сделали в предыдущем примере.

В школе тему раскрытия скобок обычно подходят в 6 классе. На этом этапе раскрытие скобок воспринимают, как избавление от скобок, которые указывают порядок выполнения действий. И изучают раскрытие скобок на примерах выражений, которые содержат:

Раскрытие скобок также можно рассматривать шире.

Раскрытием скобок можно назвать переход от выражения, которое содержит отрицательные числа в скобках, к выражению без скобок. Например:

Или, если в описанных выше выражениях вместо чисел и переменных могут быть любые выражения. В полученных таким способом выражениях тоже можно проводить раскрытие скобок. Например:

Раскрытие скобок — это избавление от скобок, которые указывают порядок выполнения действий, а также избавление от скобок, в которые заключены отдельные числа и выражения.

Важно отметить еще один момент, который касается особенностей записи решения при раскрытии скобок. При раскрытии скобок в громоздких выражениях можно прописывать промежуточные результаты в виде цепочки равенств. Например, вот так:

Первое правило раскрытия скобок

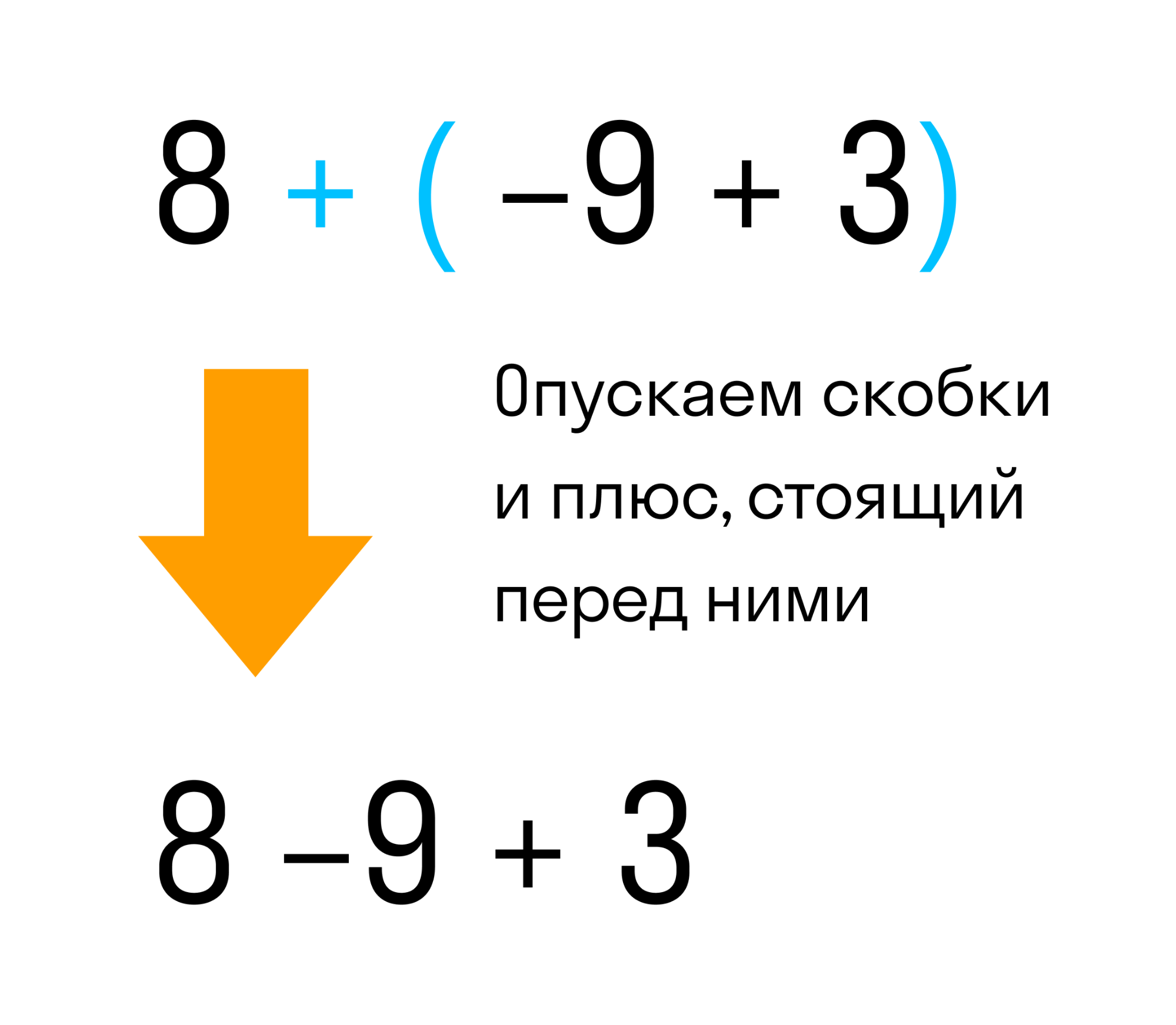
Это выражение равно двум. А теперь раскроем скобки, то есть избавимся от них. Мы ожидаем, что после избавления от скобок значение выражения 8 + (−9 + 3) также должно быть равно 2.

Первое правило раскрытия скобок

Если перед скобками стоит знак плюс — все числа, которые стоят внутри скобок, сохраняют свой знак.

Формула раскрытия скобок

Мы видим что в выражении 8 + (−9 + 3) перед скобками стоит плюс. Значит плюс нужно опустить вместе со скобками. То, что было в скобках — запишем без изменений, вот так:

Так мы получили выражение без скобок 8 − 9 + 3. Снова получаем в результате вычисления два.

Поэтому между выражениями 8 + (−9 + 3) и 8 − 9 + 3 можно поставить знак равенства, поскольку они равны одному и тому же значению:

Потренируемся применять правило на примерах.

Пример 1. Раскрыть скобки в выражении 8 + (−3 − 1)

Перед скобками стоит плюс, значит этот плюс опустим вместе со скобками. А то, что было в скобках оставим без изменений:

Пример 2. Раскрыть скобки в выражении 6 + (−2)

Перед скобками стоит плюс, значит применим то же правило:

Раскрытие скобок в предыдущих пример выглядит, как обратная операция замены вычитания сложением.

В выражении 6 − 2 происходит вычитание, но его можно заменить сложением. Тогда получится выражение 6 + (−2). Но если в выражении 6 + (−2) раскрыть скобки, то получится снова 6 − 2.

Поэтому первое правило раскрытия скобок можно использовать для упрощения выражений после любых других преобразований.

Идем дальше. Теперь упростим выражение 2a + a − 5b + b.

Чтобы упростить такое выражение, нужно привести подобные слагаемые. Для этого нужно сложить коэффициенты подобных слагаемых и результат умножить на общую буквенную часть:

Получили выражение 3a + (−4b). Раскроем скобки. Перед скобками стоит плюс, поэтому используем первое правило раскрытия скобок: опустим скобки вместе с плюсом, который стоит перед этими скобками.

Таким образом, выражение 2a + a − 5b + b упрощается до 3a − 4b.

После открытия одних скобок, по пути можно найти другие. К ним применяем те же правила, что и к первым. Например, раскроем скобки в таком выражении:

Здесь нужно раскрыть скобки в двух местах. Снова применяем первое правило раскрытия скобок, а именно опускаем скобки вместе с плюсом, который стоит перед:

Пример 3. Раскрыть скобки 6 + (−3) + (−2)

В обоих местах перед скобками стоит плюс. Применяем первое правило раскрытия скобок:

Можно встретить такой пример, когда первое слагаемое в скобках записано без знака. Например, в выражении 1 + (2 + 3 − 4) первое слагаемое в скобках 2 записано без знака. Какой знак будет стоять перед двойкой после того, как скобки и плюс, стоящий перед скобками опустятся? Ответ интуитивно понятен — перед двойкой будет стоять плюс.

Дело в том, что даже в скобках перед двойкой стоит плюс, просто мы его не видим так как плюс не принято записывать. Полная запись положительных чисел выглядит так: +1, +2, +3, но плюсы по традиции не записывают, поэтому положительные числа мы всегда видим в таком виде: 1, 2, 3.

Поэтому, чтобы раскрыть скобки в выражении 1 + (2 + 3 − 4), нужно как обычно опустить скобки вместе с плюсом, который стоит перед этими скобками, но первое слагаемое которое было в скобках записать со знаком плюс:

Пример 4. Раскрыть скобки в выражении (−7)

Перед скобками стоит плюс, но мы его не видим так как до него нет других чисел или выражений. Убираем скобки, применив первое правило раскрытия скобок:

Пример 5. Раскрыть скобки 9a + (−5b + 6c) + 2a + (−2d)

Видим два места, где нужно раскрыть скобки. В обоих участках перед скобками стоит плюс, значит этот плюс опускается вместе со скобками. То, что было в скобках запишем без изменений:

Второе правило раскрытия скобок

Здесь рассмотрим второе правило раскрытия скобок. Звучит так:

Второе правило раскрытия скобок

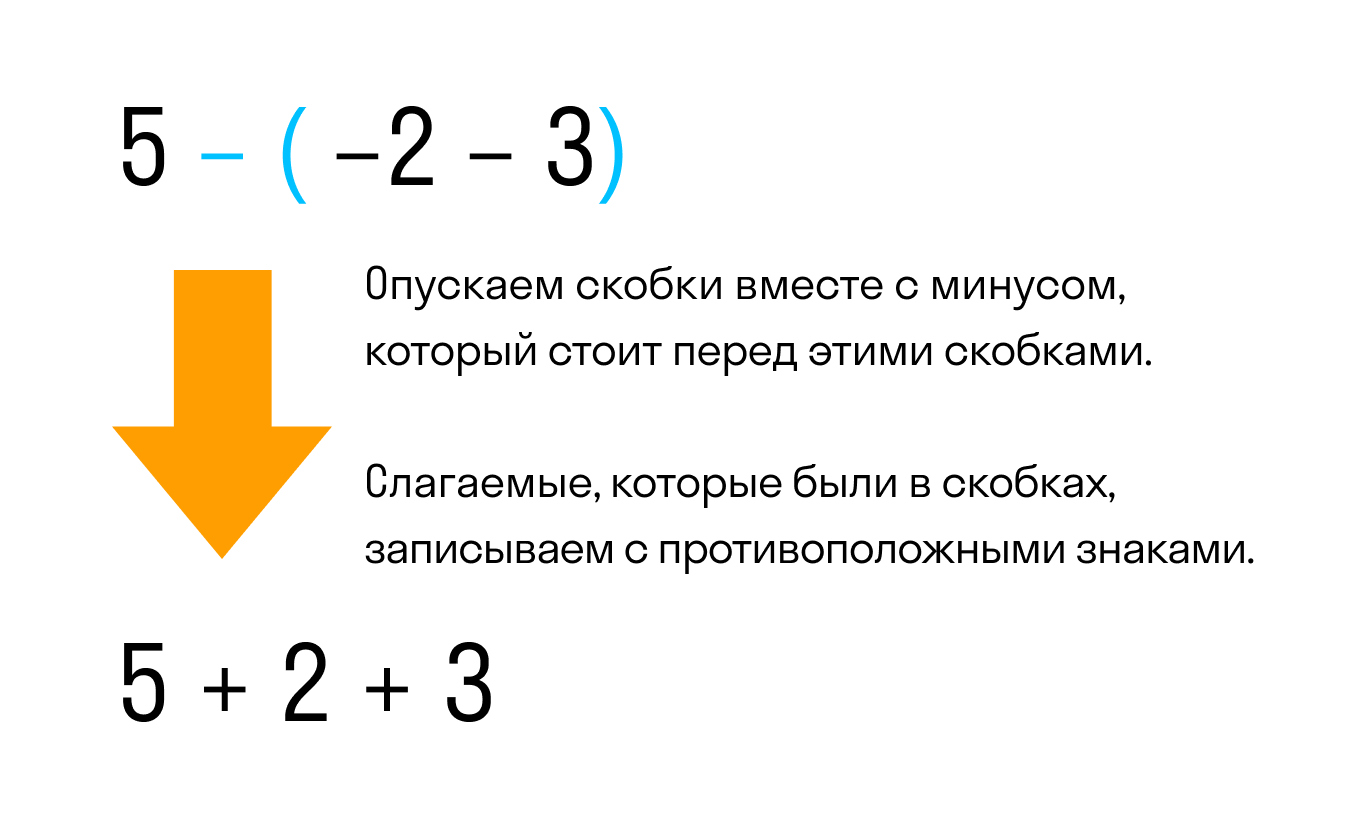
Если перед скобками стоит знак минус — все числа, которые стоят внутри скобок, меняют свой знак на противоположный.

Формула раскрытия скобок

Например, раскроем скобки в выражении 5 − (−2 − 3)

Видим, что перед скобками стоит минус. Значит нужно применить второе правило раскрытия, а именно опустить скобки вместе с минусом, который стоит перед этими скобками. При этом слагаемые, которые были в скобках, поменяют свой знак на противоположный:

Так мы получили выражение без скобок 5 + 2 + 3. Это выражение равно десяти, как и предыдущее выражение со скобками было равно 10.

Поэтому между выражениями 5 − (−2 − 3) и 5 + 2 + 3 можно поставить знак равенства так как они равны одному и тому же значению:

Пример 1. Раскрыть скобки в выражении 18 − (−1 − 5)

Перед скобками стоит минус, поэтому применим второе правило раскрытия скобок:

Пример 2. Раскрыть скобки −(−6 + 7)

Перед скобками стоит минус, поэтому применим второе правило раскрытия скобок:

Пример 3. Раскрыть скобки −(−7 − 4) + 15 + (−6 − 2)

Здесь мы видим два места, где нужно раскрыть скобки. В первом случае применим второе правило раскрытия скобок, а во втором — первое правило:

−(−7 − 4) + 15 + (−6 − 2) = 7 + 4 + 15 − 6 − 2

Пример 4. Раскрыть скобки в выражении a − (3b + 3) + 10

Перед скобками стоит минус, поэтому применим второе правило раскрытия скобок:

a − (3b + 3) + 10 = a − 3b − 3 + 10

Другие правила раскрытия скобок

Правило раскрытия скобок при делении

Если после скобок стоит знак деления — каждое число внутри скобок делится на делитель, который стоит после скобок.

Формула раскрытия скобок

Деление скобки на число предполагает, что необходимо разделить на число все заключенные в скобки слагаемые.

Деление можно предварительно заменить умножением, после чего можно воспользоваться подходящим правилом раскрытия скобок в произведении. Это же правило применимо и при делении скобки на скобку.

Например, нам необходимо раскрыть скобки в выражении (x + 2) : 2/3. Для этого сначала заменим деление умножением на обратное число:

Далее умножим скобку на число:

Правило раскрытия скобок при умножении:

Если перед скобками стоит знак умножения — каждое число, которое стоит внутри скобок, нужно умножить на множитель перед скобками.

Формула раскрытия скобок

Пример 1. Раскрыть скобки 5(3 − x)

В скобке у нас стоят 3 и −x, а перед скобкой — пятерка. Значит, каждый член скобки нужно умножить на 5:

Знак умножения между числом и скобкой в математике не пишут для сокращения размеров записей.

Пример 2. Упростить выражение: 5(x + y) − 2(x − y)

Как решаем: 5(x + y) − 2(x − y) = 5x + 5y − 2x + 2y = 3x + 7y.

Таблица с формулами раскрытия скобок

Эти таблицы с правилами раскрытия скобок можно распечатать и обращаться к ним, когда возникнут сомнения в ходе решения задачки.

Правила раскрытия круглых скобок вида (-a), в которых находится одночлен

Правила раскрытия круглых скобок, в которых находится многочлен

Скобки убирают, знаки всех слагаемых в скобках не меняют, если:

Скобки убирают, знаки всех слагаемых в скобках меняются на противоположные, если:

Раскрытие круглых скобок при умножении одночлена на многочлен

Раскрытие круглых скобок при умножении многочлена на многочлен

Раскрытие круглых скобок при возведении многочлена в степень

(a + b)2 = (a + b)(a + b) = a(a + b) + b(a + b)= a2 + ab + ab + b2 = a2 + 2ab + b2

Скобка в скобке

В 7 классе на алгебре можно встретить задачи со скобками, которые вложены внутрь других скобок. Вот пример такого задания:

Чтобы успешно решать подобные задания, нужно:

При этом важно при раскрытии одной из скобок не трогать все остальное выражение и просто переписывать его, как есть. Разберем подробнее тот же самый пример.

Пример 1. Раскрыть скобки и привести подобные слагаемые 7x + 2(5 − (3x + y))

Начнем с раскрытия внутренней скобки (той, что внутри). Раскрывая ее, имеем дело только с тем, что к ней непосредственно относится – это сама скобка и минус перед ней. Всё остальное переписываем также как было.

Теперь раскроем вторую скобку, внешнюю:

Упростим получившееся выражение:

Порядок раскрытия скобок

Теперь рассмотрим порядок применения правил, разобранных выше в выражениях общего вида. То есть в выражениях, которые содержат суммы с разностями, произведения с частными, скобки в натуральной степени.

Порядок раскрытия скобок согласован с порядком выполнения действий:

Пример 1. Раскрыть скобки и упростить выражение:

Значение выражения не зависит от переменной и всегда отрицательно. Что и требовалось доказать.

Задачи для самостоятельного решения

На алгебре в 6 и 7 классе придется решать задачки с раскрытием скобок много и часто. Поэтому лучше запомнить правила и практиковаться уже сейчас.

Задание 6. Раскройте скобки:

Задание 7. Раскройте скобки:

Источник

Как легко понять знаки Σ и П с помощью программирования

Для тех, кто подзабыл матешу

Вот говорят, что если ты не закончил Физтех, ФПМ или Бауманку, тебе в программировании делать нечего. Почему так говорят? Потому что, дескать, ты не учил сложную математику, а в программировании без неё никуда.

Это всё чушь, конечно. Если вы плохо знаете математику, вы можете быть блестящим разработчиком. Вы вряд ли напишете драйверы для видеокарты, но вы запросто сделаете мобильное приложение или веб-сервис. А это — основные деньги в этой среде.

Но всё же, чтобы получить некоторое интеллектуальное превосходство, вот вам пара примеров из страшного мира математики. Пусть они покажут вам, что не все закорючки в математике — это ад и ужас. Вот две нестрашные закорючки.

Знак Σ — сумма

Когда математикам нужно сложить несколько чисел подряд, они иногда пишут так:

Σ (читается «сигма») — это знак алгебраической суммы, который означает, что нам нужно сложить все числа от нижнего до верхнего, а перед этим сделать с ними то, что написано после знака Σ.

На картинке выше написано следующее: «посчитать сумму всех чисел от 5 до 15, умноженных на два». То есть:

Давайте для закрепления ещё один пример. На картинке ниже будет сказано «Найди сумму квадратов чисел от 5 до 10». То есть «возьми все числа от 5 до 10, каждое из них возведи в квадрат, а результаты сложи».

Но мы с вами как программисты видим, что здесь есть повторяющиеся действия: мы много раз складываем числа, которые меняются по одному и тому же правилу. А раз мы знаем это правило и знаем, сколько раз надо его применить, то это легко превратить в цикл. Для наглядности мы показали, какие параметры в Σ за что отвечают в цикле:

Произведение П

С произведением в математике работает точно такое же правило, только мы не складываем все элементы, а перемножаем их друг на друга:

А если это перевести в цикл, то алгоритм получится почти такой же, что и в сложении:

Что дальше

Сумма и произведение — простые математические операции, пусть они и обозначаются страшными символами. Впереди нас ждут интегралы, дифференциалы, приращения и бесконечные ряды. С ними тоже всё не так сложно, как кажется на первый взгляд.

Источник

Общая характеристика

Главная задача знаков — описание этапов осуществляемых действий. Математическое уравнение или выражение имеет одиночную пару квадратных, фигурных и других скобок, а также может использовать их некоторое количество.

Значение и разновидности

Скобки — это парные знаки, используемые во всевозможных областях. Чтобы правильно выстроить фразу в русском языке, для понимания смысла текста в предложении они употребляются как знаки препинания. С начальных классов школы изучают основы этих знаков.

В расчетах первая из скобок считается открывающей, а вторая — замыкающей. Оба знака соответствуют друг другу, но также используются те, в которых открытие или закрытие не различается (косые /…/, прямые скобки |…|, двойные прямые ||…||. Раскрывать значение можно чаще всего в математике, физике, химии и остальных науках для указания важности выполнения операции в формулах. На компьютерной клавиатуре представлены все виды знаков препинания.

Разновидности:

Открытие круглых () произошло в 1556 году для подкоренного выражения. По правилу первым выполняется действие внутри знака, затем произведение или определение частного (деление), а в конце — суммирование и разница.

В Microsoft word, Excel включена электронная конфигурация этих знаков. Часто используемые виды скобок, следующие: (), [ ], < >(), [ ], < >. Также встречаются двойные, называемые обратными (]] и [ [) или > в виде уголка. Их использование является двойственным — с открывающейся и замыкающей скобочкой.

Основные цели квадратной скобки в математике:

Другие варианты расчета:

Квадратные скобки в математике обозначают, что действие выполняется последовательно. Эти знаки позволяют разграничить операции.

Треугольные актуальны в теории групп. Правило записи ⟨ a ⟩ n характеризует циклическую группу порядка n, сформированную элементом a.

Круглые (операторные) () используются в математике для описания первостепенности действий. Например, (1 +5)*3 означает, что нужно сначала сложить 1 и 5, а затем полученную величину перемножить на 3. Наряду с квадратными, используются для записи разных компонент векторов, матриц и коэффициентов.

На уроке математики преподаватель объясняет, как раскрыть скобки в уравнении для последующего решения. Фигурная одинарная < встречается при решении систем уравнений, обозначает пересечение данных, а [[ используется при их слиянии.

Одинарные или двойные выражения

Употребление [] происходит реже. Одно уравнение со скобками объединяет несколько значений или неравенств различных размеров. Для решения совокупности нужно выполнить любое условие. Конец, завершение действия замыкает закрывающий знак.

В персональных компьютерах, ноутбуках, нетбуках встроена кодировка Юникод, закрепленная не за левыми или правыми объединяющими знаками, а за открывающими и замыкающими, поэтому при воспроизведении печатного текста со скобочками в режиме «справа налево» каждый знак меняет внешнее направление на обратное.

Квадратные скобки в уравнении означают, что установлен порядок действий, задаются границы промежутков и необходимость выполнения действия над выражением. Двойные квадратные скобки необходимы для записи выражений наряду с круглыми для рационального порядка действий.

По правилам интервал [−a;+a] записывается в виде нестрогого неравенства −a≤x≤a, означающего, что x находится на промежутке от −a до a включительно.

В середине парного знака с отделяющей точкой или запятой указываются два числа — наименьшее, затем большее, ограничивающие интервал. Круглая скобочка, прилегающая к цифре, означает невключение числа в промежуток, а квадратная — добавление.

В некоторых учебных пособиях для вузов встречаются расшифровки числовых интервалов, в которых вместо круглой скобочки (применяется обратная квадратная скобка ], и наоборот. В обозначениях запись ]0, 1[ равносильна (0, 1).

Открытая квадратная скобка (символ [) значит, что совокупность представляет систему уравнений разных размеров, для которых справедливы все множества решений для каждого уравнения, входящего в общее задание. Например, [x+11=2yy2−12=0

Прежде чем решать задачу или выполнять задание, нужно правильно определить принципы действий. В некоторых случаях скобочки могут быть не нужны, а иногда их обязательно нужно поставить.

Прочие знаки

Для математических, алгебраических и прочих расчетов важно знать различие обобщающих знаков. От правильности вычислений зависит итоговый результат.

Удобство записи системы уравнений

Применение фигурных знаков относится к представлению совмещения множеств. При решении системы с фигурной скобкой уравнения пересекаются, а [] объединяет их.

Источник

Что значит смайлик написанный символами — значения обозначений и расшифровка текстовых смайлов

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Не так давно мы с вами довольно подробно обсудили тему использования смайликов в социальной сети Вконтакте. Там же были приведены основные коды Emoji-смайлов (около тысячи — на все случаи жизни). Если вы с той публикацией еще не ознакомились, то настоятельно рекомендую это сделать:

Однако, приведенные в упомянутой статье коды хоть и являются универсальными (Emoji-смайлы подойдут и для Твиттера), но в некоторых местах их вставки могут и не сработать (не преобразоваться в нужную вам картинку смайлика). Таких мест встретится немного, но они все же есть. Кроме этого, довольно утомительно будет каждый раз открывать приведенную выше страницу с кодами, чтобы вставить в текст грустный, плачущий, подмигивающий или улыбающийся смайл (то есть наиболее часто выражаемые в сообщениях эмоции).

Что же делать? Все очень просто. Нужно будет только запомнить нужные вам комбинации символов, которые будут понятны всем, кто прочитает ваше сообщение (а во многих случаях вместо этих текстовых смайлов пользователи будут видеть нужные картинки, что вообще замечательно). Но как узнать что значит тот или иной смайлик? Где посмотреть их обозначения? Обо всем этом вы узнаете из продолжения этой публикации.

Обозначение эмоций символами в первых текстовых смайлах

В современной письменной речи практически нет возможности быстро отобразить эмоции, которые обуревают автора текста в момент его написания. С этим не было никаких проблем вплоть до эры повального распространения интернета (всегда было время описать свое состояние парой фраз или предложений). Но с появление всемирной паутины и увеличением доли общения путем написания сообщений (в чате, на форуме, в мессенджере и т.п.) сложившееся положение вещей многих перестало устраивать.

Ведь в интернете письменное общение очень часто идет в режиме реального времени и собеседникам просто-напросто некогда подбирать слова, которые помогут выразить эмоции. Ну, например, для восхищения можно использовать восклицательный знак, а для вопроса — вопросительный. Но как показать, что это шутка или, наоборот, что вы говорите на полном серьезе?

Эту проблему решил один из пионеров общения в сети еще в начале восьмидесятых годов прошлого века. В частности, он предложил добавлять к шуточным сообщениям символы 🙂 т.е. текстовый вариант улыбающегося лица, положенного на бок — что означает, по сути, смеющийся смайлик 🙂

Начало было положено, и затем уже человеческую фантазию ничто удержать не могло. Основной упор опять же делался на быстрое выражение эмоций с помощью набора символов, но в обиход также вошли и смысловые смайлы обозначающие действия, состояния и т.п. Никакого стандартизированного набора текстовых смайликов не существует до сих пор, но есть варианты, которые используются наиболее часто, и именно о них мы сегодня и поговорим.

Вы их видите только благодаря тому, что на вашем компьютере стоит набор шрифтов в формате Юникода, куда зашиты не только такие причудливые значки, но даже около 1000 кодов Emoji-смайлов, о которых мы уже говорили. Еще несколько примеров интересных символов сложившихся в смайлы:

Что они означают вы уж сами догадайтесь. А если не догадались, но они вам понравились и вы хотите больше, то милости просим в каталог текстовых и символьных смайликов.

Что значат текстовые смайлики составленные из символов?

Мы же с вами давайте продолжим изучать значения наиболее распространенных вариантов написания тех или иных смайликов с помощью обычных (невычурных) символов. Готовы? Ну, тогда поехали.

Обозначение символами смайликов эмоций

Значение текстовых смайликов эмоциональных действий или жестов

Что значат горизонтальные (японские) символьные смайлы?

Изначально так повелось, что большинство из придуманных и получивших распространение текстовых смайликов нужно было расшифровывать как бы „наклонив голову набок“. Однако это не совсем удобно, согласитесь. Поэтому со временем стали появляться их аналоги (тоже набранные из символов), которые не требовали виртуально или реально наклонять голову вбок, ибо создаваемое символами изображение было расположено горизонтально.

Давайте рассмотрим, что значат наиболее распространенные из горизонтальных текстовых смайлов:

Естественно, что на многих блогах и форумах уже давным-давно имеется возможность добавлять смайлики в виде картинок (из готовых наборов), но многие по-прежнему продолжают использовать текстовые смайлы, ибо уже набили на этом руку и при этом нет необходимости отыскивать в каталоге нужную картинку.

Кроме этого многие движки форумов или блогов (как, например, WordPress, на котором работает этот блог) умеют преобразовывать символы смайликов в реальные изображения, что еще больше добавляет удобства. Можете попробовать в комментариях к этому посту вставить символы улыбающегося или плачущего смайлика и увидите, что он преобразуется в картинку. Можете также посмотреть коды смайлов для вставки в WordPress.

Если хотите узнать, что значит тот или иной набор символов, являющийся текстовым смайликом, то пишите об этом в комментариях. Авось всем миром и разберемся.

Источник