что значит счетное множество
Разнообразие бесконечностей
Бесконечные множества содержат неограниченную последовательность элементов, объединенных общим признаком. Самые часто используемые из них в математике:
Все они бесконечны, вовсе не означает, что они равномощны.
Сравнение и отображение
Числа в математике можно сравнивать друг с другом и выяснять, какое из них больше. С множествами можно производить аналогичные действия. Это будет называться их отображение друг в друга. Оно может быть дизъюнктивно, конъюнктивно и биективно. Это аналог числовых понятий «больше», «меньше» и «равно». Для того чтобы разобраться, как происходит это сравнение, нужно понятие подмножества.
Подмножеством некоторого набора компонентов называется любая часть компонентов этого набора. То есть, совокупность состоящее из чисел 1 и 3 является подмножеством множества чисел 1, 3 и 5. А они оба, в свою очередь, являются подмножествами совокупности нечётных чисел и т. д.
Если каждому компоненту множества A можно сопоставить какой-то элемент подмножества совокупности В, то отображение А в В конъюнктивно или А меньше, чем В. Если при этом нельзя найти в наборе А подмножество, которое можно сопоставить с совокупностью В, то отображение В в А дизъюнктивно. Если же каждому компоненту из комплекса А можно сопоставить элемент из совокупности В и каждому компоненту из набора В можно сопоставить элемент из совокупности А, то эти множества отображаются друг в друге биективно. В таком случае говорят, что они эквивалентны.
Для сравнения совокупностей можно использовать их мощность. Если мощность А меньше мощности В, то и множество А меньше, чем В. Если мощности равны, то сами наборы элементов эквивалентны.
Сопоставление наборов элементов
Казалось бы, используя свойства сравнения наборов элементов, можно найти соотношение мощностей бесконечных совокупностей. Ведь очевидно, что множество N является подмножеством совокупности Z, они оба являются подмножеством Q, а множества Q и I вместе составляют R. И отсюда, по определению, следует, что мощности соотносятся так: |N| |I|, и загадкой остается только соотношение совокупностей Q и I. Но всё не так просто.
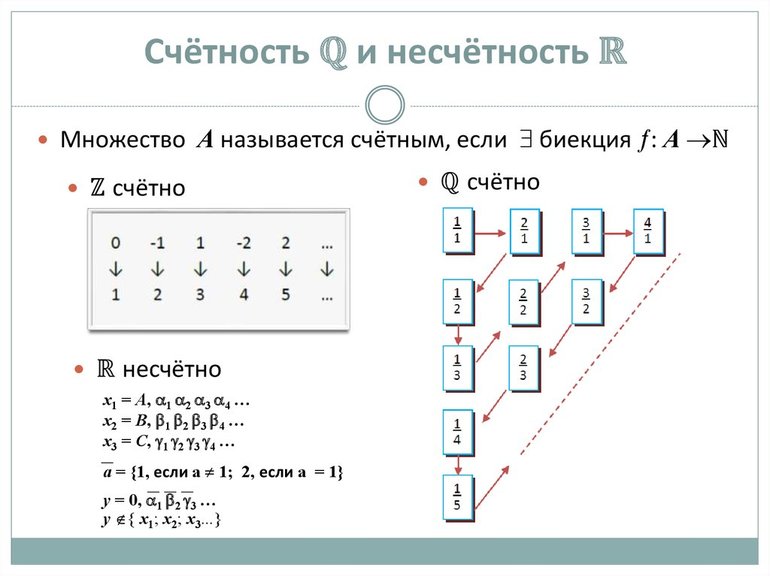
Выяснение размера бесконечного комплекса компонентов — такая же задача, как определение размера конечной совокупности — пересчёт компонентов. Возможность посчитать и пронумеровать элементы бесконечной совокупности называется счётностью. Совокупность натуральных чисел — счётная. Элементам в этом случае легко присвоить порядковые номера. И все множества, которые эквивалентны N, тоже будут счётными. Его размер |N| = a.
Но если взять R, то его элементы пронумеровать не получится. Ведь между любыми двумя точками, а прямой всегда можно поставить ещё одну. То есть, совокупность R «бесконечна вглубь»: каждый промежуток между бесконечным количеством точек содержит в себе бесконечное количество точек. Значит, свойство R — несчётность. Такие «бесконечные вглубь» множества называют континуальными. И их мощность обозначается как |R| = c.
Ещё одно важное свойство бесконечных множеств заключается в том, что если из бесконечной совокупности удалить (или добавить к ней) подмножество меньшей мощности, то размер исходной совокупности сохранится. Если из N убрать все числа от 1 до 10, то его мощность не уменьшится на 10, а останется прежней. Множество останется бесконечным и счётным: a — 10 = a.
Бесконечная мощность счётных и несчётных множеств может быть описана тремя формулами. Это два равенства и одно неравенство:
Совокупность всех точек интервала или отрезка на прямой тоже будет континуальна, так как на неё можно спроецировать всю совокупность точек действительной прямой R.
Соотношение мощностей
Континуальное множество больше счётного. Но какова их разница? Чтобы это вычислить, потребуется понятие булеан.
Что такое булеан
Есть некий набор компонентов V. Булеаном V будет называться комплекс всех его подмножеств. Как будут соотноситься размер булеана и самого V? Если V состоит из одного элемента, то его булеан будет состоять из двух элементов: пустого набора компонентов и самого V. Если V состоит из двух элементов, то булеан содержит 4 элемента: пустое множество, V и каждый из двух элементов. Если V содержит 3 элемента, то булеан содержит 8: пустое, само V, каждый из трёх его элементов в отдельности и каждую пару элементов (которых тоже три).
То есть мощность булеана — это 2 в степени размера самого V. Булеан так и записывается 2^|V|. Размер булеана всегда будет больше, чем мощность самой совокупности.
Результат сопоставления
Размер булеана любой счётной совокупности будет 2^a. Если рассматривать N, то его булеан будет состоять из пустоты, бесконечного числа элементов N, бесконечного числа пар элементов, бессчётного числа сочетаний элементов по 3, 4, 5 и так до бесконечности. Какому известному множеству можно сопоставить этот булеан?
Так как это N — натуральные числа, то каждый элемент булеана — это последовательность чисел. Если представить каждую такую последовательность в виде знаков после запятой в десятичной дроби, то получатся координаты точек в интервале от 0 до 1, который эквивалентен R. Так как булеан N содержит бесконечное количество комбинации бесконечных десятичных дробей, то он покрывает все точки в этом интервале. Это нестрогое доказательство уравнения c = 2^a.
Обозначения мощностей а и c происходят от слов account и continum, но именно такая последовательность букв порождает вопрос: а есть ли бесконечное множество мощностью b, которое меньше c, но больше a. Если и есть, то пока они неизвестны. А вот комплекс больший по мощности, чем c, есть. Это булеан континуального множества с мощностью 2^c. А у этого булеана тоже есть булеан с ещё большей мощностью.
Бесконечные множества бывают счётными и несчётными. Счётными называют те, элементы в которых можно пересчитать, то есть эквивалентные совокупности натуральных чисел. К ним относятся само множество натуральных, а также целых и рациональных чисел. Среди несчётных выделяют континуальные множества, эквивалентные совокупности всех точек на прямой. К ним относятся действительные и иррациональные числа. Континуальность является булеаном счётного набора.
Счётные и несчётные множества — понятие, свойства и примеры
Множество — это совокупность или набор элементов. Количество этих элементов называется мощностью этой совокупности. Мощность пустого набора компонентов равна нулю. С размером конечных совокупностей тоже всё просто. У них можно пересчитать количество компонентов. А вот возможность посчитать компоненты бесконечности различает счётные и несчётные множества.
Разнообразие бесконечностей
Бесконечные множества содержат неограниченную последовательность элементов, объединенных общим признаком. Самые часто используемые из них в математике:
Все они бесконечны, вовсе не означает, что они равномощны.
Сравнение и отображение
Числа в математике можно сравнивать друг с другом и выяснять, какое из них больше. С множествами можно производить аналогичные действия. Это будет называться их отображение друг в друга. Оно может быть дизъюнктивно, конъюнктивно и биективно. Это аналог числовых понятий «больше», «меньше» и «равно». Для того чтобы разобраться, как происходит это сравнение, нужно понятие подмножества.
Подмножеством некоторого набора компонентов называется любая часть компонентов этого набора. То есть, совокупность состоящее из чисел 1 и 3 является подмножеством множества чисел 1, 3 и 5. А они оба, в свою очередь, являются подмножествами совокупности нечётных чисел и т. д.
Если каждому компоненту множества A можно сопоставить какой-то элемент подмножества совокупности В, то отображение А в В конъюнктивно или А меньше, чем В. Если при этом нельзя найти в наборе А подмножество, которое можно сопоставить с совокупностью В, то отображение В в А дизъюнктивно. Если же каждому компоненту из комплекса А можно сопоставить элемент из совокупности В и каждому компоненту из набора В можно сопоставить элемент из совокупности А, то эти множества отображаются друг в друге биективно. В таком случае говорят, что они эквивалентны.
Для сравнения совокупностей можно использовать их мощность. Если мощность А меньше мощности В, то и множество А меньше, чем В. Если мощности равны, то сами наборы элементов эквивалентны.
Сопоставление наборов элементов
Казалось бы, используя свойства сравнения наборов элементов, можно найти соотношение мощностей бесконечных совокупностей. Ведь очевидно, что множество N является подмножеством совокупности Z, они оба являются подмножеством Q, а множества Q и I вместе составляют R. И отсюда, по определению, следует, что мощности соотносятся так: |N| |I|, и загадкой остается только соотношение совокупностей Q и I. Но всё не так просто.
Выяснение размера бесконечного комплекса компонентов — такая же задача, как определение размера конечной совокупности — пересчёт компонентов. Возможность посчитать и пронумеровать элементы бесконечной совокупности называется счётностью. Совокупность натуральных чисел — счётная. Элементам в этом случае легко присвоить порядковые номера. И все множества, которые эквивалентны N, тоже будут счётными. Его размер |N| = a.
Но если взять R, то его элементы пронумеровать не получится. Ведь между любыми двумя точками, а прямой всегда можно поставить ещё одну. То есть, совокупность R «бесконечна вглубь»: каждый промежуток между бесконечным количеством точек содержит в себе бесконечное количество точек. Значит, свойство R — несчётность. Такие «бесконечные вглубь» множества называют континуальными. И их мощность обозначается как |R| = c.
Ещё одно важное свойство бесконечных множеств заключается в том, что если из бесконечной совокупности удалить (или добавить к ней) подмножество меньшей мощности, то размер исходной совокупности сохранится. Если из N убрать все числа от 1 до 10, то его мощность не уменьшится на 10, а останется прежней. Множество останется бесконечным и счётным: a — 10 = a.
Поскольку N отображается в R конъюнктивно (N является подмножеством R, но не имеет подмножества эквивалентного R), то |R|=c > a=|N|. А так как R представляет собой объединение совокупностей Q и I, то размер |I| = |R| — |Q| = c — a = c. Значит, I тоже континуально.
Бесконечная мощность счётных и несчётных множеств может быть описана тремя формулами. Это два равенства и одно неравенство:
Совокупность всех точек интервала или отрезка на прямой тоже будет континуальна, так как на неё можно спроецировать всю совокупность точек действительной прямой R.
Соотношение мощностей
Континуальное множество больше счётного. Но какова их разница? Чтобы это вычислить, потребуется понятие булеан.
Что такое булеан
Есть некий набор компонентов V. Булеаном V будет называться комплекс всех его подмножеств. Как будут соотноситься размер булеана и самого V? Если V состоит из одного элемента, то его булеан будет состоять из двух элементов: пустого набора компонентов и самого V. Если V состоит из двух элементов, то булеан содержит 4 элемента: пустое множество, V и каждый из двух элементов. Если V содержит 3 элемента, то булеан содержит 8: пустое, само V, каждый из трёх его элементов в отдельности и каждую пару элементов (которых тоже три).
То есть мощность булеана — это 2 в степени размера самого V. Булеан так и записывается 2^|V|. Размер булеана всегда будет больше, чем мощность самой совокупности.
Результат сопоставления
Размер булеана любой счётной совокупности будет 2^a. Если рассматривать N, то его булеан будет состоять из пустоты, бесконечного числа элементов N, бесконечного числа пар элементов, бессчётного числа сочетаний элементов по 3, 4, 5 и так до бесконечности. Какому известному множеству можно сопоставить этот булеан?
Так как это N — натуральные числа, то каждый элемент булеана — это последовательность чисел. Если представить каждую такую последовательность в виде знаков после запятой в десятичной дроби, то получатся координаты точек в интервале от 0 до 1, который эквивалентен R. Так как булеан N содержит бесконечное количество комбинации бесконечных десятичных дробей, то он покрывает все точки в этом интервале. Это нестрогое доказательство уравнения c = 2^a.
Обозначения мощностей а и c происходят от слов account и continum, но именно такая последовательность букв порождает вопрос: а есть ли бесконечное множество мощностью b, которое меньше c, но больше a. Если и есть, то пока они неизвестны. А вот комплекс больший по мощности, чем c, есть. Это булеан континуального множества с мощностью 2^c. А у этого булеана тоже есть булеан с ещё большей мощностью.
Бесконечные множества бывают счётными и несчётными. Счётными называют те, элементы в которых можно пересчитать, то есть эквивалентные совокупности натуральных чисел. К ним относятся само множество натуральных, а также целых и рациональных чисел. Среди несчётных выделяют континуальные множества, эквивалентные совокупности всех точек на прямой. К ним относятся действительные и иррациональные числа. Континуальность является булеаном счётного набора.
Введение в теорию множеств
Концепция бесконечности идеологически далека от обычной математической терминологии — ни одна другая тема не выходит за пределы математики так, что превращается из практического, аналитического инструмента в явление мифического порядка. Понятие бесконечности на короткой ноге с такими культурными темами, как религия и философия, и окутана загадочной аурой божественности.
Когда-то давным давно во всех академических дисциплинах было заложено фундаментальное убеждение — существует единственная бесконечность.
Но 1874 году довольно малоизвестный математик провёл серию революционных наблюдений, подвергавших сомнению это всеми принятое и глубоко укоренившееся убеждение. Георг Кантор в своей (теперь уже ставшей легендарной) публикации On a Property of the Collection of All Real Algebraic Numbers доказал, что множество вещественных чисел «более многочисленно», чем множество алгебраических чисел. Так он впервые показал, что существуют бесконечные множества разных размеров (не волнуйтесь — для прояснения этого мы вскоре подробно изучим его статью).
«Множество — это большое количество, которое позволяет воспринимать себя как одно» — Георг Кантор
С 1874 по 1897 год Кантор неистово публиковал статью за статьёй, разворачивая свою теорию абстрактных множеств в расцветающую дисциплину. Однако она была встречена упорным сопротивлением и критикой; многие педанты считали, что его теории перешли в область философии и нарушили принцип религии.
Однако когда начали находиться практические применения математического анализа, отношение к теории изменилось, а идеи и результаты Кантора начали получать признание. К первому десятилению 20-го века его наблюдения, теории и публикации достигли своей кульминации — признания современной теории множеств новой, совершенно уникальной областью математики:
Теория множеств — это математическая теория о точно определённых наборах (множествах) отдельных объектов, называемых членами или элементами множества.
Сколько чисел есть между 0 и 1?
Первая публикация Кантора, состоящая из четырёх с половиной страниц, является великолепным примером краткости. Она разделена на два отдельных доказательства, совместно приводящих к выводу о существовании по крайней мере двух уникальных видов множеств.
В первой части теории исследуется множество вещественных алгебраических чисел и доказывается, что это бесконечное счётное множество. Здесь не стоит путать — «счётное» не обязательно значит, что счёт ведётся строго в целых числах; в контексте теории множеств «счётное» означает, что множество, пусть даже состоящее из бесконечного числа элементов, можно описать повторяющимся рядом, например упорядоченной многочленной функцией. Кантор назвал это свойство бесконечного набора чисел соответствия «один к одному» с рядом, наличием взаимно однозначного соответствия.
Если говорить вкратце, то набор, или множество всех вещественных алгебраических чисел можно вывести с помощью какого-то теоретического ряда многочленов с различными степенями и коэффициентами; следовательно, множество всех вещественных алгебраических чисел является бесконечным счётным множеством.
Во второй части труда Кантора анализируется роль вещественных комплексных чисел, также называющихся трансцендентными числами. Транцендентные числа (лучшие примеры которых — это пи и e) имеют любопытное свойство: математически невозможно вывести их с помощью многочленной функции — они не являются алгебраическими. Вне зависимости от величин, количества частей, степеней или коэффициентов, никакой ряд никогда не может посчитать пи в своём наборе бесконечного счётного множества.
Затем Кантор указывает, что в любом замкнутом интервале [a,b] существует хотя бы одно транцендентное число, которое никогда нельзя будет подсчитать в бесконечном счётном множестве. Поскольку одно такое число существует, то предполагается, что в семействе вещественных чисел существует бесконечное количество транцендентных чисел.
Таким образом он доказал очень чёткое различие между множеством непрерывных, идущих потоком несчётных чисел и набора счётных чисел, которые можно представить как ряд, например, всех вещественных алгебраических чисел.
Далее: запись и операции
Первая публикация Кантора завершилась на этом потрясающем подтверждении существования по крайней мере двух разных видов бесконечности. После его первой статьи появился шквал дополнений, медленно, но верно прокладывавших путь к современной теории множеств.
Стоит также поделиться интересным наблюдением: большинство людей, использующих теорию множеств на практике, ценят скорее не эту конкретную теорему, а заданный ею обобщённый язык. Благодаря своей абстрактной природе теория множеств скрытно влияет на множество областей математики. В математическом анализе, который требует дифференциального и интегрального исчисления, необходимо понимание пределов и непрерывности функций, окончательно закреплённых в теории множеств. В алгебре логики логические операции «и», «или» и «не» соответствуют операциям пересечения, объединения и разности в теории множеств. И последнее, но не менее важное — теория множеств закладывает основы топологии — исследования геометрических свойств и пространственных отношений.
Вооружившись базовым пониманием истории множеств и совершив кратковременное погружение в глубины его влияния, мы можем приступать к знакомству с основами системы обозначений теории множеств.
Часть вторая. Краткий обзор операций, обозначений и диаграмм Венна.
Как сказано в предыдущей части, одно из фундаментальных преимуществ теории множеств произрастает не из какой-то конкретной теории, а из созданного ею языка. Именно поэтому основная часть этого раздела будет посвящена обозначениям, операциям и визуальному представлению теории множеств. Давайте начнём с объяснения базовых символов обозначения множества — соответствующих ему элементов. В таблице ниже показан пример одного множества A с тремя элементами:
A — это множество с элементами «1», «2» и «3»
«1» — элемент множества A
В первой строке показано множество A с тремя отдельными элементами (A = ); во второй строке показан правильный способ обозначения отдельного конкретного элемента 1, принадлежащего множеству A. Пока всё довольно просто, но теория множеств становится существенно интереснее, когда мы добавляем второе множество — начинается путешествие по стандартным операциям.
Операции: пересечение (intersection) — множество элементов, принадлежащих множеству A и множеству B;
объединение (union) — множество элементов, принадлежащих множеству A или множеству B;
подмножество (subset) — C является подмножеством A, множество C включено во множество A;
собственное (истинное) подмножество — C является подмножеством A, но C не равно A;
относительное дополнение (relative complement) — множество элементов, принадлежащих к A и не к B.
Вот и они, самые распространённые операции в теории множеств; они довольно популярны и в областях за пределами чистой математики. На самом деле, высока вероятность того, что вы уже видели подобные типы операций в прошлом, хоть и не совсем с такой терминологией, и даже пользовались ими. Хорошая иллюстрация: попросите любого студента описать диаграмму Венна из двух пересекающихся групп, и он интуитивно придёт к правильному результату.
Ещё раз взгляните на последнюю строку, относительное дополнение — какое необычное сочетание слов, правда? Относительное к чему? Если относительное дополнение A — B определяется как A и не B, то как нам обозначить всё, что не является B?
Универсальное множество — пустое множество
Оказывается, если мы хотим получить значимый ответ, то для начала нужно предоставить генеральной совокупности нашей задачи множеств некий контекст. Он часто явным образом задаётся в начале задачи, когда допустимые элементы множества ограничиваются некоторым фиксированным классом объектов, в котором существует универсальное множество, являющееся общим множеством, содержащим все элементы для этой конкретной задачи. Например, если мы хотели бы работать со множествами только из букв английского алфавита, то наше универсальное множество U состояло бы из 26 букв алфавита.
Для любого подмножества A множества U дополнение множества A (обозначаемое A′ или U − A) определяется как множество всех элементов в генеральной совокупности U, которое не находится в A. Если вернуться к поставленному выше вопросу, то дополнением множества B является всё в пределах универсального множества, что не принадлежит B, в том числе и A.
Прежде чем мы двинемся дальше, надо упомянуть ещё одно принципиальное множество, которое достаточно важно для базового понимания: нулевое или пустое множество. Учтите, что существует единственное пустое множество, поэтому никогда не говорят «пустые множества». Хотя мы не будем рассматривать в этой статье эквивалентность, основная теория гласит, что два множества эквивалентны, если они имеют одинаковые элементы; следовательно, может быть только одно множество без элементов. Поэтому существует единственное пустое множество.
Диаграммы Венна и остальное
Диаграммы Венна, официально изобретённые в 1880 году Джоном Венном, являются именно тем, что вы и представляете, хотя их научное определение звучит примерно так:
Схематичное изображение всех возможных отношений нескольких множеств
Ниже показано изображение шести самых распространённых диаграмм Венна, и почти во всех показаны недавно изученные нами операнды:
Объединение (union), пересечение (intersection), относительное дополнение (relative complement), симметрическая разность (symmetric difference), собственное множество (proper subset), абсолютное дополнение (universal дополнение).
Начав с очень простых обозначений множества и его элементов, мы узнали затем о базовых операциях, позволивших нарисовать эту визуальную подсказку. Мы рассмотрели все операции, за исключением симметрической разности (внизу слева). Чтобы не оставлять пробелов в знаниях, скажем, что симметрическая разность, также называемая дизъюнктивным объединением — это просто множество элементов, которые находятся в любом из множеств, но не входят в их пересечение.
Закончим мы этот раздел введением понятия мощности (кардинального числа). Мощность множества, обозначаемая символом абсолютного значения — это просто количество уникальных элементов, содержащихся в определённом множестве. Для показанного выше примера мощность трёх множеств равна: |A| = 3, |B| =6, |C| = 2.
Прежде чем двигаться дальше, дам вам пищу для размышлений — какова связь между мощностью и количеством возможных подмножеств?
Часть 3. Мощность и показательные множества
В предыдущих двух частях мы разобрались с основами теории множеств. В третьей части мы укрепим своё понимание, сосредоточившись на самом важном свойстве любого множества: общем количестве содержащихся в нём уникальных элементов.
Количество уникальных элементов во множестве, также известное как мощность, предоставляет нам фундаментальную опорную точку для дальнейшего, более глубокого анализа этого множества. Во-первых, мощность — это первое из рассматриваемых нами уникальных свойств, позволяющее нам объективно сравнивать различные виды множеств, проверяя, существует ли биекция (это, с небольшими оговорками, просто более изысканный термин для function ) одного множества на другое. Ещё один способ применения мощности, а также тема этой части статьи — мощность позволяет оценить все возможные подмножества, существующие в данном множестве. Что достаточно буквально можно применять в повседневных задачах распределения решений, будь то планирование бюджета на поездку в продуктовый магазин или оптимизация портфеля акций.
Примеры мощности множеств
Например, в таблице выше показаны пять отдельных множеств с их указанной справа мощностью. Как мы уже говорили, символ мощности напоминает символ абсолютного значения — значение, заключённое между двумя вертикальными линиями. Все примеры понятны, за исключением, возможно, последней строки, которая подчёркивает тот факт, что на мощность влияют только уникальные элементы множества.
Помните подмножества из предыдущей части статьи? Оказывается, что мощность некоторого множества A и количество возможных подмножеств множества A имеют удивительную связь. Ниже показано, что количество подмножеств, которые можно составить из некоторого подмножества, увеличивается с порядком мощности на предсказуемую величину:
Количество возможных подмножеств в C= 2 |C|
Давайте подробно рассмотрим показанный ниже пример. Однако для начала поразмыслим над формулой. Представим мощность как общее количество «позиций», которое представляет множество. При создании некоторого подмножества для каждой возможной позиции принимается булево решение (да/нет). Это означает, что каждый уникальный элемент, добавляемый к множеству (то есть увеличивающий мощность на единицу) увеличивает количество возможных подмножеств на множитель два. Если вы программист или учёный, то можете уяснить эту логику немного глубже, если поймёте, что все подмножества множества можно вычислить с помощью таблицы двоичных чисел.
Показательное множество (булеан)
Прежде чем мы вычислим все подмножества для примера множества C, я хотел бы ввести последнее понятие — булеан.
Булеан обозначается заглавной буквой S, за которой в скобках указывается исходное множество S(С). Булеан — это множество всех подмножеств C, включая пустое множество и само множество C. В таблице ниже показан булеан S(С) со всеми перестановками возможных подмножеств для множества C, содержащихся в одном большом множестве.
Для удобства форматирования я убрал запятые между множествами***
Чем может быть полезен булеан? На самом деле, вы скорее всего много раз интуитивно использовали булеаны, даже об этом не догадываясь. Каждый раз, когда вы выбираете подмножество элементов из более крупного множества, вы выбираете элемент булеана. Например ребёнок внимательно изучающий кондитерский магазин с купюрой в 5 долларов — какой элемент булеана множества всех доступных сладостей он выберет? Или если взять более технический пример: вам, как разработчику ПО может потребоваться запросить всех возможных пользователей базы данных, также обладающих свойством X и Y — ещё один случай, в котором одно подмножество выбирается из всех возможных подмножеств.
Эквивалентность и биективная функция
Теперь мы понимаем, что такое мощность множества, почему оно важно, и его связь с булеаном. Поэтому вернёмся ненадолго к тому, что упоминали в самом начале: что конкретно определяет эквивалентность в теории множеств?
Очевидно, что два множества с одинаковой мощностью имеют некое общее свойство, но на этом сходства заканчиваются — что если в одном из множеств есть многократно повторяющийся элемент? Что если два множества имеют одинаковую мощность и количество элементов? Нельзя отрицать, что они в какой-то степени «эквивалентны», но даже в этом случае всё равно есть возможность различий, потому что каждое множество может иметь разные элементы, повторяющиеся одинаковое количество раз. Смысл здесь в том, что концепция эквивалентности в теории множеств немного чужда другим областям математики. Установление эквивалентности в этом мире требует знакомства с этой концепцией и нового языка. В последней части этой статьи мы введём понятие эквивалентности, а также таких базисных свойств, как инъективные, биективные и сюръективные функции.
Часть 4. Функции.
В этой части мы подробнее расскажем о функциях в пределах теории множеств. Как и в случае с предыдущими понятиями, терминология стандартных функций в теории множеств слегка отличается от других областей математики, а потому требует объяснения. Терминологии довольно много, так что давайте сразу приступим к делу! В первой таблице внизу отражены понятия области определения, области значений и значения функции:
Функция в мире теории множеств — это просто соответствие некоторых (или всех) элементов из Множества A некоторым (или всем) элементам Множества B. В показанном выше примере набор всех возможных элементов A называется областью определения; элементы A, используемые в качестве входных значений, в частности называются аргументами. Справа набор всех возможных выходных значений (называющихся в других областях математики «областью значений»), называется кообластью; набор настоящих выходных элементов B, соответствующих A, называется образом.
Пока особо ничего сложного, только новый способ задания параметров функций. Далее мы расскажем о том, как описывать поведения этих функций соответствия при помощи обычных типов функций.
Инъекции, сюръекции и биекции
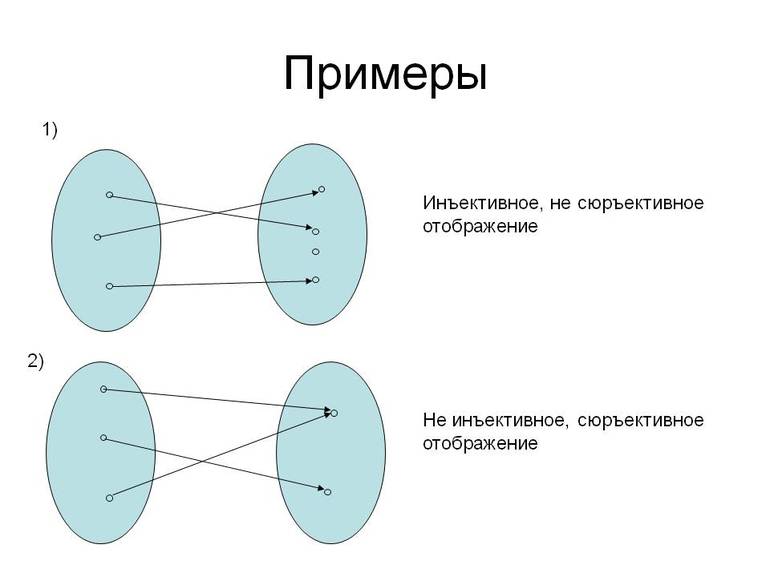
В теории множеств для классификации соответствия множеств обычно используются три понятия: инъекция, сюръекция и биекция. К сожалению, эти понятия имеют несколько разных названий, усиливающих неразбериху, поэтому мы сначала рассмотрим каждое определение, а затем изучим визуальные примеры. Все три термина описывают способ, которым отображаются аргументы на образы:
Прочитайте заново представленный выше список пунктов. Биекция — это просто функция, удовлетворяющая обоим предыдущим требованиям; то есть, функция инъективна и сюръективна. Инъективная функция не должна быть сюръективной, а сюръективная — инъективной. Ниже показан визуальный пример, в котором эти три классификации привели к созданию функций множеств, определяемых четырьмя возможными комбинациями инъективных и сюръективных свойств:
Биекция (инъекция + сюръекция), инъекция (инъекция + не-сюръекция), сюръекция (не-инъекция + сюръеция), без классификации (не-инъекция + не-сюръекция)
Вот и всё! Теперь мы обладаем элементарным пониманием самых часто встречаемых соотношений, встречающихся в мире множеств. Однако это ни в коем случае не конец нашего пути: напротив, это самое начало.
Фундаментальные основы теории множеств — ключ к пониманию более высокоуровневых областей математики. Чтобы продолжить наше движение вверх, к этим различным областям, далее нужно будет, пользуясь своими знаниями о теории множеств, уяснить одну из самых революционных теорий в истории математики: систему аксиом Цермело-Френкеля.