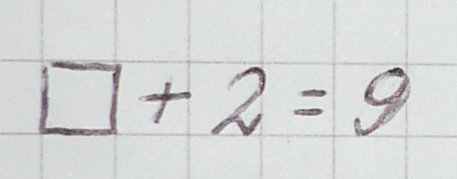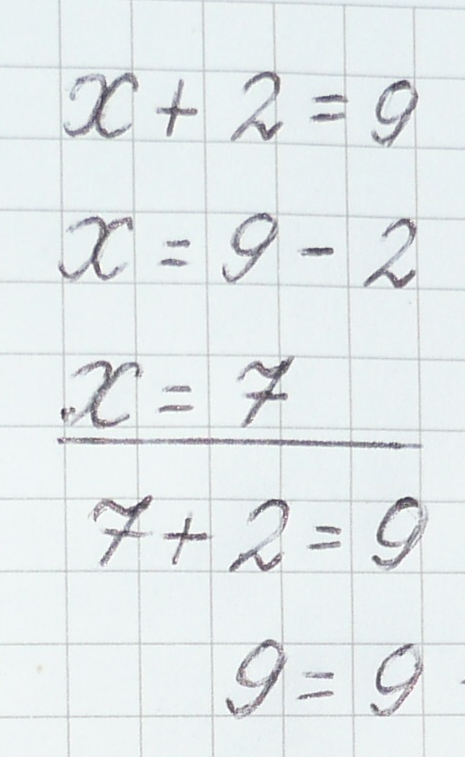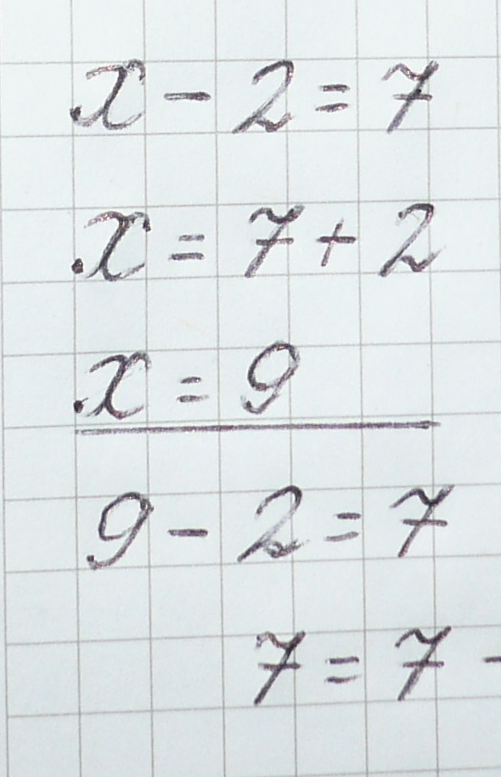что значит сделать проверку уравнения

17.11.202323.04.2022 admin 0 Comments

Что такое уравнение и корни уравнения? Как решить уравнение?

Уравнения бывают разные. Вы изучите их многие виды в курсе математике, но все они решаются по одним правилам, эти правила мы сейчас рассмотрим подробно.

Что такое уравнение? Смысл и понятия.

Узнаем сначала все понятия, связанные с уравнением.

Определение:
Уравнение – это равенство, содержащее переменные и числовые значения.

Переменные (аргументы уравнения) или неизвестные уравнения – их обозначают в основном латинскими буквами (x, y, z, f и т.д.). При подстановки числового значения переменной в уравнение получаем верное равенство – это корень уравнения.

Решить уравнение – это значит найти все корни уравнения или доказать, что у данного уравнения нет корней.

Корни уравнения – это значение переменной при котором уравнение превращается в верное равенство.

Рассмотрим теперь, все термины на простом примере:
x+1=3

В данном случае x – переменная или неизвестное значение уравнения.

Можно устно решить данное уравнение. Какое надо число прибавить к 1, чтобы получить 3? Конечно, число 2. То есть наша переменная x =2. Корень уравнения равен 2. Проверим правильно ли мы решили уравнение? Чтобы проверить уравнение, нужно вместо переменной подставить полученный корень уравнения.

Получили верное равенство. Значит, правильно нашли корни уравнения.

Но бывают более сложные уравнения, которые устно не решить. Нужно прибегать к правилам решения уравнений. Рассмотрим правила решения уравнений ниже, которые объяснят нам как решать уравнения.

Правила уменьшения или увеличения уравнения на определенное число.

Чтобы понять правило рассмотрим подробно простой пример:
Решите уравнение x+2=7

Решение:
Чтобы решить данное уравнение нужно левую и правую часть уменьшить на 2. Это нужно сделать для того, чтобы переменная x осталась слева, а известные (т.е. числа) справа. Что значит уменьшить на 2? Это значит отнять от левой части двойку и одновременно от правой части отнять двойку. Если мы делаем какое-то действие, например, вычитание применяя его одновременно к левой части уравнения и к правой, то уравнение не меняет смысл.

Как проверить правильно ли вы нашли корень уравнения? Ведь не все уравнения будут простыми как данное. Чтобы проверить корень уравнения его значение нужно поставить в само уравнение.

Проверка:
Вместо переменной x подставим 5.

x+2=7
5+2=7
Получили верное равенство, значит уравнение решено верно.
Ответ: 5.

Разберем следующий пример:
Решите уравнение x-4=12.

Решение:
Чтобы решить данное уравнение нужно увеличить левую и правую часть уравнения на 4, чтобы переменная x осталось в левой стороне, а известные (т.е. числа) в правой стороне. Прибавим к левой и правой части число 4. Получим:

Теперь выполним проверку, вместо переменной x подставим в уравнение полученное число 16.
x-4=12
16-4=12
Ответ: 16

Очень важно понять правила переноса частей уравнения через знак равно. Не всегда нужно переносить числа, иногда нужно перенести переменные или даже целые выражения.

Рассмотрим пример:
Решите уравнение 4+3x=2x-5

Теперь, когда все неизвестные в левой стороне, а все известные в правой стороне посчитаем их.
(3-2)x=-9
1x=-9 или x=-9

Получилось верное равенство, уравнение решено верно.
Ответ: корень уравнения x=-9.

Правила уменьшения или увеличения уравнения в несколько раз.

Данное правило подходит тогда, когда вы уже посчитали все неизвестные и известные, но какой-то коэффициент остался перед переменной. Чтобы избавится от не нужного коэффициента мы применяем правило уменьшения или увеличения в несколько раз коэффициент уравнения.

Рассмотрим пример:
Решите уравнение 5x=20.

Решение:
В данном уравнение не нужно переносить переменные и числа, все компоненты уравнения стоят на месте. Но нам мешает коэффициент 5 который стоит перед переменной x. Мы не можем его просто взять и перенести в правую сторону уравнения, потому что между число 5 и переменно x стоит умножение 5⋅х. Если бы между переменной и числом стоял знак плюс или минус, мы могли бы 5 перенести вправо. Но мы так поступить не можем. За то мы можем все уравнение уменьшить в 5 раз или поделить на 5. Обязательно делим правую и левую сторону одновременно.

5x=20
5x :5 =20 :5
5:5x=4
1x=4 или x=4

Делаем проверку уравнения. Вместо переменной x подставляем 4.
5x=20
5⋅ 4 =20
20=20 получили верное равенство, корень уравнение найден правильно.
Ответ: x=4.

Решение:
Так как перед переменной x стоит коэффициент необходимо от него избавиться. Надо все уравнение увеличить в 3 раза или умножить на 3, обязательно умножаем левую часть уравнения и правую часть.

Сделаем проверку уравнения. Подставим вместо переменной x полученный корень уравнения 21.

7=7 получено верное равенство.

Ответ: корень уравнения равен x=21.

Следующий пример:
Найдите корни уравнения

Далее делим все уравнение на 3.

Сделаем проверку. Подставим в уравнение найденный корень.

Как решать уравнения? Алгоритм действий.

Подведем итог разобранной теме уравнений, рассмотрим общие правила решения уравнений:

Эти правила действуют на любой вид уравнения (линейный, квадратный, логарифмический, тригонометрический, рациональные, иррациональные, показательные и другие виды). Поэтому важно понять эти простые правила и научиться ими пользоваться.

Источник

Математика. 4 класс

Конспект урока

Математика, 4 класс

Урок 21. Решение уравнений

Перечень вопросов, рассматриваемых в теме:

Уравнение – это равенство с неизвестным числом. Неизвестное число обозначают латинской буквой.

Решить уравнение – это значит найти значение неизвестного, при котором равенство будет верным.

Корень уравнения – это значение неизвестного, обозначенного латинской буквой в уравнении.

Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.

Обязательная и дополнительная литература по теме урока:

1. Моро М. И. Учебник для 4 класса четырехлетней начальной школы. М. «Просвещение» — 2017.С. 62,63

2. Волкова Е. В. математика Всероссийская проверочная работа за курс начальной школы. Издательство «Экзамен» 2018.С.27

3. Петерсон Л. Г. математика 3 класс. Часть 2. Ювента, 2015.-96с.: ил. С.77-78

Теоретический материал для самостоятельного изучения:

Являются ли эти записи уравнениями?

Это не уравнения, так как в уравнении должен быть знак «=». Это выражения.

Уравнение – это равенство с неизвестным числом. Неизвестное число обозначают латинской буквой.

Рассмотрите другие записи:

Это уравнения, так как это равенства, содержащие переменную.

Попробуем их решить.

Что значит решить уравнение?

Решить уравнение – это значит найти значение неизвестного, при котором равенство будет верным.

Вспомните алгоритм решения уравнений.

Используя алгоритм, решите первое уравнение

Значение неизвестного х = 25. Это корень уравнения.

Корень уравнения – это значение неизвестного, обозначенного латинской буквой в уравнении. В данном случае – это х.

Можно ли решить второе уравнение, используя этот же алгоритм?

Такие уравнения не рассматривались. Какова же цель нашего урока?

Цель урока: научиться решать уравнения, в которых в ответе не число, а числовое выражение.

Такие уравнения мы будем называть составные. Поэтому тема урока: «Решение составных уравнений»

Чтобы решить это уравнение, нужно упростить правую часть.

Ответ: корень уравнения 25

Составим алгоритм решения составных уравнений.

Алгоритм решения составных уравнений

1. Найти значение числового выражения.

2. Вспомнить компоненты действия данного уравнения.

3. Определить неизвестный компонент.

4. Вспомнить правило нахождения неизвестного компонента.

5. Применить правило и найти неизвестный компонент.

7. Сделать проверку.

Решим еще одно уравнение:

Применяем алгоритм решения составных уравнений:

3. Определить неизвестный компонент.

4. Вспомнить правило нахождения неизвестного компонента.

5. Применить правило и найти неизвестный компонент.

7. Сделать проверку.

Ответ: корень уравнения 12

Вывод: чтобы решить составное уравнение, в которых в ответе не число, а числовое выражение, необходимо упростить правую часть ( т.е решить выражение), после чего получаем уравнение известного вам вида и решаем его, используя алгоритм решения уравнений.

Решим задачу, составив уравнение:

Сумма неизвестного числа и числа 390 равна произведению чисел 70 и 6. Найди это число.

1. Сумма неизвестного числа и числа 390 – обозначим неизвестное число переменной х, тогда получим х + 390

2. Произведение чисел 70 и 6: 70 ∙ 6

3. Получаем уравнение: х + 390 = 70 ∙ 6

Применяя алгоритм решения составных уравнений, решим его:

Источник

Начальные классы. Уравнения.

С уравнениями ученики знакомятся в 1 классе. Сначала решают примеры с окошком: выполняют действия с числами и задания на нахождение неизвестного числа, например было равенство:

И одно число решили спрятать:

Нам нужно догадаться, что за число спрятали?
Здесь прекрасно видно, чтобы найти неизвестное число, нужно из 9 — 2
Искомое число – 7.

В нашем равенстве – искомое число называют неизвестным числом.
А равенство, в котором одно число стало неизвестным, называется УРАВНЕНИЕМ.
Никто из вас никогда не видел, чтобы уравнения делали с «окошком». Это неудобно. Гораздо проще неизвестное обозначать буквами.

Неизвестное число обозначают маленькими латинскими буквами

или любой другой буквой.

И этому числу дают имя – корень уравнения.
Давайте посмотрим записи:
8+х
8+х>5
8+х =10
Только третья запись — уравнение. Потому что здесь есть неизвестное число и знак =.
Нам необходимо узнать это число.
Найти все значения х, при котором равенство будет верным — значит, решить уравнение, т.е. найти его корень.

При решении уравнения учитываем взаимосвязи между целым и частью:
— чтобы найти целое, надо сложить части;
— чтобы найти часть, надо из целого вычесть другую часть.

Если вы хотите более подробно узнать, как связаны целое и части, читайте тут.

Решение записывается так:

Корень пишем на следующей строке и подчеркиваем прямой линией.

Корень уравнения = 7, следовательно, наше уравнение решено.
Нам обязательно нужно проверить правильно мы нашли корень уравнения или нет.
Уравнение без проверки – это не уравнение.
Итак, в нашем уравнении корень –7, мы его подчеркнули, а теперь сделаем проверку. Для этого мы переписываем первую строку уравнения, но вместо неизвестного поставим значение корня.
Теперь: знак = пишем под знаком =. Число, записанное справа от знака равно: 9 – переписываем. Выражение, которое находится слева от знака равно: 7 + 2 – считаем. Получится 9. Это число 9 записываем слева от знака =.
Читаем выражение: 9 = 9. Значит, уравнение решили правильно.

Решим еще одно уравнение:

Ученикам начальной школы нужно обязательно овладеть математической речью. Для этого нужно знать, как называются компоненты при различных действиях, и как находится неизвестный компонент:

Если из суммы вычесть одно из слагаемых, то получится другое слагаемое.
Если к разности прибавить вычитаемое, то получится уменьшаемое.
Если из уменьшаемого вычесть разность, то получится вычитаемое.

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 5 / 5. Количество оценок: 65

Источник

Решение простых линейных уравнений

Понятие уравнения

Понятие уравнения обычно проходят в самом начале школьного курса алгебры. Его определяют, как равенство с неизвестным числом, которое нужно найти.

В школьной программе за 7 класс впервые появляется понятие переменных. Их принято обозначать латинскими буквами, которые принимают разные значения. Исходя из этого можно дать более полное определение уравнению.

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.

Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.

Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.

Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.

Решить уравнение значит найти все возможные корни или убедиться, что их нет.

Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.

Какие бывают виды уравнений

Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.

Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.

Линейное уравнение выглядит так	ах + b = 0, где a и b — действительные числа. Что поможет в решении: Система уравнений — это несколько уравнений, для которых нужно найти значения неизвестных. Она имеет вид ax + by + c = 0 и называется линейным уравнением с двумя переменными x и y, где a, b, c — числа. Решением этого уравнения называют любую пару чисел (x; y), которая соответствует этому выражению и является верным числовым равенством. Числовой коэффициент — число, которое стоит при неизвестной переменной. Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз: Как решать простые уравнения Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила. 1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный. Для примера рассмотрим простейшее уравнение: x+3=5 Начнем с того, что в каждом уравнении есть левая и правая часть. Перенесем 3 из левой части в правую и меняем знак на противоположный. Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2. Решим еще один пример: 6x = 5x + 10. 2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок. Применим правило при решении примера: 4x=8. При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение. Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица. Разделим каждую часть на 4. Как это выглядит: Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения: Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: −4x = 12 Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах. Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные. Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки. Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте схему-подсказку — храните ее в телефоне, учебники или на рабочем столе. А вот и видео «Простейшие линейные уравнения» для тех, кто учиться в 5, 6 и 7 классе. Примеры линейных уравнений Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе! Пример 1. Как правильно решить уравнение: 6х + 1 = 19. Пример 2. Как решить уравнение: 5(х — 3) + 2 = 3 (х — 4) + 2х — 1. 5х — 15 + 2 = 3х — 2 + 2х — 1 Ответ: х — любое число. Пример 3. Решить: 4х = 1/8. Пример 4. Решить: 4(х + 2) = 6 — 7х. Пример 5. Решить: Пример 6. Как решить линейное уравнение: х + 7 = х + 4. 5х — 15 + 2 = 3х — 2 + 2х — 1 Пример 7. Решить: 2(х + 3) = 5 — 7х.. Источник Урок математики в 1-м классе по теме: «Уравнение. Проверка решения уравнения» I. Организационный момент. Ученики за партами поворачиваются лицом друг к другу. Один ученик раскрывает свои ладошки, а другой накрывает их своими ладонями, улыбаются, желают друг другу удачной работы. II. Актуализация знаний. 1) Счет до 10 и обратно. Даны три числа 6; 4; 10. — назовите число, которое является суммой двух других чисел; — назовите наименьшее и наибольшее число; — на сколько 10 больше 4; на сколько 4 меньше 10; — как узнать, на сколько одно число больше или меньше другого; — замените каждое из чисел суммой одинаковых слагаемых. 2) Какие числа надо записать в «окошках»? + 4 = 9 — 3 = 7 3 + = 10 Как найти неизвестные компоненты? — Лишнее неравенство 10 > а. — Лишним может быть также равенство 3 + 2 = 5, потому что только в этом равенстве все компоненты известные. — Как называются равенства, в которых есть неизвестный компонент? — Такие равенства называются уравнениями. 3) Задание №1 учебника, с.64. Помоги Вове отметить в уравнениях и на схеме целое и части и подобрать к уравнениям нужные схемы. Выполняем задание, формулируем основное правило. Как найти неизвестное целое. Как найти неизвестную часть. Называем компоненты действий в каждом из уравнений. III. «Открытие» нового знания и формулирование темы урока. Выполняем задание №2, с.64. Как Лене заполнить схему к каждому уравнению и решить уравнения? Аргументируем свои действия с помощью введенного правила. — А вдруг решения найдены неверно? Ведь мы могли ошибиться в вычислениях, а это также ошибка. Как вы думаете, что нам делать, чтобы избежать ошибок? 2) Текст под знаком Как можно проверить, верно ли мы решили уравнения? Дети высказывают свои предположения. — Петя, Катя и Вова сделали проверку решения наших уравнений. Они хорошо умеют это делать и могут научить нас. Давайте посмотрим, как они это сделали, и постараемся научиться этому сами. — Как ребята делали проверку? (Они брали число, которое получили при решении уравнения (значение х) и подставляли его вместо буквы.) — Что они делали потом? (Находили значение выражения, которое у них получилось.) Что означают числа в этих равенствах? (Здесь сравнили числа, которые стояли в уравнениях после знака равенства и значение выражения, которое получили, когда вместо х подставили его значение.) — Какое же число можно назвать решением уравнения? (Решение уравнения – это такое число, которое мы можем записать (подставить в уравнение) вместо буквы, выполнить с ним действие, которое записано в уравнении, и получим то же число. которое стояло в уравнении после знака равенства.) — Что нового мы с вами узнали? (Узнали, как делать проверку решения уравнения.) — Полезно это знание для нас? — Как вы думаете, чем мы с вами сегодня будем заниматься на уроке? IV. Первичное закрепление изученного. Выполняем на доске с комментированием по опорной записи задание № 4 (первое и второе уравнения): а) пишу: х + 4 = 9; б) отмечаю целое и части. Неизвестна часть; в) чтобы найти неизвестную часть надо из целого вычесть другую часть. Пишу: х = 9 – 4; г) пишу: х равен пяти; д) делаю проверку: подставляю вместо х в уравнение найденное число. Пять плюс четыре равно 9; е) х – 4 равно девяти и 5 + 4 равно девяти, значит х равен 5. V. Самостоятельная работа. Третье уравнение решаем самостоятельно в тетради с последующей проверкой и комментированием по ходу работы. VI. Тренировочные упражнения и задания на повторение. Помоги ребятам решить задачи. Записываем решение задач в тетрадь самостоятельно с последующей проверкой. — Придумайте, пожалуйста, к условию каждой из задач еще один вопрос. 2) Совместно ищем решение задачи № 6 на с.65. — Петя задумал число. Потом он прибавил к нему 4, из суммы вычел 5, к разности прибавил 2 и в результате получил число 3. Какое число задумал Петя? — Какие предложите решения? — Задуманное число обозначим через х и составим уравнение. — Какое получится уравнение? — Как решим такое уравнение? — Выполним обратные действия! 3 – 2 + 5 – 4 = 2. — Как ответим на вопрос задачи? — Петя задумал число 2. — Есть другой способ решения задачи? — Можно составить цепочку. Чтобы найти задуманное число, из 3 вычтем 2, прибавим 5, вычтем 4 и получим 2. Каких предметов и чисел нет на рисунке? 4) Задание № 9 – для индивидуальной работы с последующей проверкой в классе. Как Лене пройти через двое ворот, чтобы набрать числа в кружках? Найди все способы. 8 – это 6 и 2 9 – это 5 и 4 — Чему научились на уроке? — Научились проверять решения уравнения. — Как вы считаете, выполнили мы сегодня план урока? – Подведите итоги своей работы. – Какие задания вызвали наибольшие затруднения? – Что понравилось на уроке? Источник ← что значит доступный кредит в орифлейм что делать если пересолена курица в духовке → Вам также понравится что такое timer resolution 18.11.202329.04.2022 admin 0 Бисфенол а где содержится чем опасен для человека 19.11.202313.08.2023 admin 0 что делать если не работает анимация в роблокс 13.11.202314.04.2022 admin 0 Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сохранить моё имя, email и адрес сайта в этом браузере для последующих моих комментариев. Курсы криптовалют сегодня: Обыграй компьютер онлайн: Ваш ход Найти на сайте Новые записи Читайте популярную книгу Август нашей жизни прямо сейчас на нашем сайте dveripetli.ru. Скачать книгу Август нашей жизни автора Женя Онегина в формате FB2, TXT, PDF, EPUB бесплатно без регистрации. Читайте популярную книгу Василиса и Кощей прямо сейчас на нашем сайте dveripetli.ru. Скачать книгу Василиса и Кощей автора Анна Геннадьевна Гринь в формате FB2, TXT, PDF, EPUB бесплатно без регистрации. Читайте популярную книгу Родня до крови прямо сейчас на нашем сайте dveripetli.ru. Скачать книгу Родня до крови автора Валерий Шарапов в формате FB2, TXT, PDF, EPUB бесплатно без регистрации. Читайте популярную книгу Квиллифер прямо сейчас на нашем сайте dveripetli.ru. Скачать книгу Квиллифер автора Уолтер Уильямс, Владимир Гольдич, Ирина Оганесова, fanzon в формате FB2, TXT, PDF, EPUB бесплатно без регистрации. Читайте популярную книгу Вариант «Бис»: Дебют. Миттельшпиль. Эндшпиль прямо сейчас на нашем сайте dveripetli.ru. Скачать книгу Вариант «Бис»: Дебют. Миттельшпиль. Эндшпиль автора Сергей Анисимов в формате FB2, TXT, PDF, EPUB бесплатно без регистрации. Комментарии пользователей Миша к записи что такое тжс в лагере Лиза к записи что такое тжс в лагере Глаша к записи что делать если у манго сохнут листья Контакты для Роскомнадзора - informationforweb2023@gmail.com Все права сохранены. © 2025 Строительный портал dveripetli.ru Внимание! Информация, опубликованная на сайте, носит исключительно ознакомительный характер и не является рекомендацией к применению. Материалы могут содержать информацию, предназначенную для пользователей старше 18 лет. 18+.

Линейное уравнение выглядит так

ах + b = 0, где a и b — действительные числа.

Что поможет в решении:

Система уравнений — это несколько уравнений, для которых нужно найти значения неизвестных. Она имеет вид ax + by + c = 0 и называется линейным уравнением с двумя переменными x и y, где a, b, c — числа.

Решением этого уравнения называют любую пару чисел (x; y), которая соответствует этому выражению и является верным числовым равенством.

Числовой коэффициент — число, которое стоит при неизвестной переменной.

Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз:

Как решать простые уравнения

Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.

1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.

Для примера рассмотрим простейшее уравнение: x+3=5

Начнем с того, что в каждом уравнении есть левая и правая часть.

Перенесем 3 из левой части в правую и меняем знак на противоположный.

Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.

Решим еще один пример: 6x = 5x + 10.

2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.

Применим правило при решении примера: 4x=8.

При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.

Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.

Разделим каждую часть на 4. Как это выглядит:

Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:

Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: −4x = 12

Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах.

Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.

Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.

Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте схему-подсказку — храните ее в телефоне, учебники или на рабочем столе.

А вот и видео «Простейшие линейные уравнения» для тех, кто учиться в 5, 6 и 7 классе.

Примеры линейных уравнений

Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе!

Пример 1. Как правильно решить уравнение: 6х + 1 = 19.

Пример 2. Как решить уравнение: 5(х — 3) + 2 = 3 (х — 4) + 2х — 1.

5х — 15 + 2 = 3х — 2 + 2х — 1

Ответ: х — любое число.

Пример 3. Решить: 4х = 1/8.

Пример 4. Решить: 4(х + 2) = 6 — 7х.

Пример 5. Решить:

Пример 6. Как решить линейное уравнение: х + 7 = х + 4.

5х — 15 + 2 = 3х — 2 + 2х — 1

Пример 7. Решить: 2(х + 3) = 5 — 7х..

Источник

Урок математики в 1-м классе по теме: «Уравнение. Проверка решения уравнения»

I. Организационный момент.

Ученики за партами поворачиваются лицом друг к другу. Один ученик раскрывает свои ладошки, а другой накрывает их своими ладонями, улыбаются, желают друг другу удачной работы.

II. Актуализация знаний.

1) Счет до 10 и обратно.

Даны три числа 6; 4; 10.

— назовите число, которое является суммой двух других чисел;
— назовите наименьшее и наибольшее число;
— на сколько 10 больше 4; на сколько 4 меньше 10;
— как узнать, на сколько одно число больше или меньше другого;
— замените каждое из чисел суммой одинаковых слагаемых.

2) Какие числа надо записать в «окошках»?

+ 4 = 9 — 3 = 7 3 + = 10

Как найти неизвестные компоненты?

— Лишнее неравенство 10 > а.

— Лишним может быть также равенство 3 + 2 = 5, потому что только в этом равенстве все компоненты известные.

— Как называются равенства, в которых есть неизвестный компонент?

— Такие равенства называются уравнениями.

3) Задание №1 учебника, с.64.

Помоги Вове отметить в уравнениях и на схеме целое и части и подобрать к уравнениям нужные схемы.

Выполняем задание, формулируем основное правило.

Как найти неизвестное целое. Как найти неизвестную часть.

Называем компоненты действий в каждом из уравнений.

III. «Открытие» нового знания и формулирование темы урока.

Выполняем задание №2, с.64.

Как Лене заполнить схему к каждому уравнению и решить уравнения?

Аргументируем свои действия с помощью введенного правила.

— А вдруг решения найдены неверно? Ведь мы могли ошибиться в вычислениях, а это также ошибка. Как вы думаете, что нам делать, чтобы избежать ошибок?

2) Текст под знаком

Как можно проверить, верно ли мы решили уравнения?

Дети высказывают свои предположения.

— Петя, Катя и Вова сделали проверку решения наших уравнений. Они хорошо умеют это делать и могут научить нас. Давайте посмотрим, как они это сделали, и постараемся научиться этому сами.

— Как ребята делали проверку? (Они брали число, которое получили при решении уравнения (значение х) и подставляли его вместо буквы.)

— Что они делали потом? (Находили значение выражения, которое у них получилось.)

Что означают числа в этих равенствах? (Здесь сравнили числа, которые стояли в уравнениях после знака равенства и значение выражения, которое получили, когда вместо х подставили его значение.)

— Какое же число можно назвать решением уравнения? (Решение уравнения – это такое число, которое мы можем записать (подставить в уравнение) вместо буквы, выполнить с ним действие, которое записано в уравнении, и получим то же число. которое стояло в уравнении после знака равенства.)

— Что нового мы с вами узнали? (Узнали, как делать проверку решения уравнения.)

— Полезно это знание для нас?

— Как вы думаете, чем мы с вами сегодня будем заниматься на уроке?

IV. Первичное закрепление изученного.

Выполняем на доске с комментированием по опорной записи задание № 4 (первое и второе уравнения):

а) пишу: х + 4 = 9;
б) отмечаю целое и части. Неизвестна часть;
в) чтобы найти неизвестную часть надо из целого вычесть другую часть.
Пишу: х = 9 – 4;
г) пишу: х равен пяти;
д) делаю проверку: подставляю вместо х в уравнение найденное число. Пять плюс четыре равно 9;
е) х – 4 равно девяти и 5 + 4 равно девяти, значит х равен 5.

V. Самостоятельная работа.

Третье уравнение решаем самостоятельно в тетради с последующей проверкой и комментированием по ходу работы.

VI. Тренировочные упражнения и задания на повторение.

Помоги ребятам решить задачи.

Записываем решение задач в тетрадь самостоятельно с последующей проверкой.

— Придумайте, пожалуйста, к условию каждой из задач еще один вопрос.

2) Совместно ищем решение задачи № 6 на с.65.

— Петя задумал число. Потом он прибавил к нему 4, из суммы вычел 5, к разности прибавил 2 и в результате получил число 3. Какое число задумал Петя?

— Какие предложите решения?

— Задуманное число обозначим через х и составим уравнение.

— Какое получится уравнение?

— Как решим такое уравнение?

— Выполним обратные действия! 3 – 2 + 5 – 4 = 2.

— Как ответим на вопрос задачи?

— Петя задумал число 2.

— Есть другой способ решения задачи?

— Можно составить цепочку.

Чтобы найти задуманное число, из 3 вычтем 2, прибавим 5, вычтем 4 и получим 2.

Каких предметов и чисел нет на рисунке?

4) Задание № 9 – для индивидуальной работы с последующей проверкой в классе.

Как Лене пройти через двое ворот, чтобы набрать числа в кружках? Найди все способы.

8 – это 6 и 2 9 – это 5 и 4

— Чему научились на уроке?

— Научились проверять решения уравнения.

— Как вы считаете, выполнили мы сегодня план урока?
– Подведите итоги своей работы.
– Какие задания вызвали наибольшие затруднения?
– Что понравилось на уроке?

Источник

Что такое уравнение и корни уравнения? Как решить уравнение?

Что такое уравнение? Смысл и понятия.

Правила уменьшения или увеличения уравнения на определенное число.

Правила уменьшения или увеличения уравнения в несколько раз.

Как решать уравнения? Алгоритм действий.

Математика. 4 класс

Конспект урока

Начальные классы. Уравнения.

Решение простых линейных уравнений

Понятие уравнения

Какие бывают виды уравнений

Как решать простые уравнения

Примеры линейных уравнений

Урок математики в 1-м классе по теме: «Уравнение. Проверка решения уравнения»

Вам также понравится

что такое timer resolution

Бисфенол а где содержится чем опасен для человека

что делать если не работает анимация в роблокс

Добавить комментарий Отменить ответ