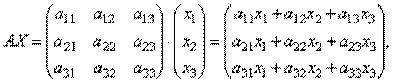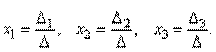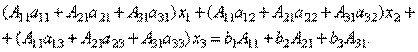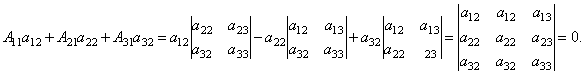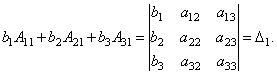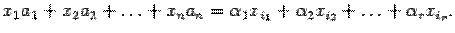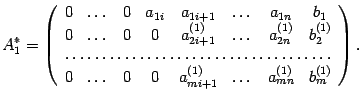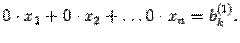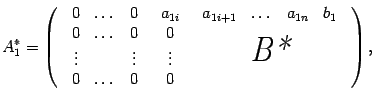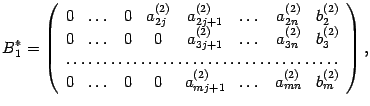что значит система несовместна
НЕСОВМЕСТНАЯ СИСТЕМА УРАВНЕНИЙ
Смотреть что такое «НЕСОВМЕСТНАЯ СИСТЕМА УРАВНЕНИЙ» в других словарях:
несовместная система уравнений — система, которая не имеет решений. Например, система 2х + у = 4, 4х + 2у = 5. * * * НЕСОВМЕСТНАЯ СИСТЕМА УРАВНЕНИЙ НЕСОВМЕСТНАЯ СИСТЕМА УРАВНЕНИЙ, система, которая не имеет решений. Напр., система … Энциклопедический словарь
Несовместная система уравнений — система, которая не имеет решений. Так, например, уравнения 2x + у = 4, 4x + 2y = 5 образуют Н. с. у. (первое из этих уравнений противоречит второму, так как если 2x + у = 4, то 4x + 2y = 8). См. Уравнение … Большая советская энциклопедия
Линейное уравнение — уравнение, в которое неизвестные входят в 1 й степени (т. е. линейно) и отсутствуют члены, содержащие произведения неизвестных. Несколько Л. у. относительно одних и тех же неизвестных образуют систему Л. у. Решением системы Л. у. называют … Большая советская энциклопедия
Линейные уравнения — [linear equations] уравнения, в которые неизвестные входят в 1 й степени (линейно) и нет членов, содержащих произведения неизвестных или экспоненты. Система линейных уравнений может иметь либо единственное решение, либо бесконечное множество… … Экономико-математический словарь
линейные уравнения — Уравнения, в которые неизвестные входят в 1 й степени (линейно) и нет членов, содержащих произведения неизвестных или экспоненты. Система линейных уравнений может иметь либо единственное решение, либо бесконечное множество решений (неопределенная … Справочник технического переводчика
Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Системы линейных уравнений
Можно доказать (см. результаты ☟ НИЖЕ ), что все возможности для произвольной системы ограничиваются следующими вариантами:
1. система совместна и имеет единственное решение;
2. cистема совместна и имеет бесконечное множество решений;
3. cистема несовместна.
Матричная форма записи
Исключение переменных (метод Гаусса)
метода достаточно проста.
Теперь осталось формализовать изложенную идею метода (сформулировав допустимые правила действия над уравнениями — те, что в принципе, очевидны из здравого смысла ), а также исследовать возможные последствия его применения к системам общего вида.
Исключение переменных
Элементарными преобразованиями системы л.у. называются преобразования следующих трех типов:
1. перестановка двух уравнений;
2. умножение обеих частей уравнения на любое отличное от нуля число;
Теорема. Любое элементарное преобразование системы л.у. переводит эту систему в ей эквивалентную, т.е. имеющую то же множество решений, что и исходная.
Задача. С помощью элементарных преобразований привести систему л.у. к наиболее простому виду: такому, из которого легко было бы установить множество решений.
Процесс получения системы такого вида из исходной системы уравнений называется прямым ходом метода Гаусса.
Исторический комментарий о Гауссе ☞ ЗДЕСЬ.
Установление множества решений
Пример. Решить систему л.у.
Ответ. Система несовместна.
Пример. Решить систему л.у.
Дальнейший матричный анализ метода Гаусса ☞ ЗДЕСЬ.
Формулы Крамера
Теорема. Cистема
Доказательство ☞ ЗДЕСЬ
Пример. Решить систему уравнений
Кроме того, формулы Крамера начинают конкурировать по вычислительной эффективности с методом Гаусса в случае систем, зависящих от параметра. Подробнее ☞ ЗДЕСЬ.
Найти достаточное условие существования общего решения систем уравнений:
Теорема Кронекера-Капелли
Доказательство достаточности проводится в следующем пункте. ♦
Система однородных уравнений
Доказать, что для совместности системы
An elementary treatise on determinants
в следующей формулировке.
Ответ ☞ ЗДЕСЬ
Общее решение
Пример. Исследовать совместность и найти общее решение системы уравнений:
Теперь посмотрим как можно описать общее решение однородной системы.
Система однородных уравнений
Теперь обсудим способы нахождения ФСР.
Оформим этот способ построения ФСР в теорему:
Пример. Найти ФСР для системы уравнений
Пример. Найти ФСР для системы уравнений
3. Еще один способ построения ФСР основан на теореме Гамильтона-Кэли.
Пример. Найти ФСР для системы уравнений
Геометрическая интерпретация
Статья не закончена!
Ортогональность
Геометрические соображения из предыдущего пункта могут быть обобщены на случай когда размерности рассматриваемых пространств увеличиваются, и мы говорим о точках и векторах многомерных пространств. В последующих пунктах нам потребуются понятия линейной оболочки, линейного пространства, размерности, базиса и координат применительно к векторам-столбцам или векторам-строкам. Их можно найти ☞ ЗДЕСЬ.
Что значит система несовместна
Решением системы называется совокупность n значений неизвестных
при подстановке которых все уравнения системы обращаются в тождества.
Система линейных уравнений может быть записана в матричном виде:
где A — матрица системы, b — правая часть, x — искомое решение, Ap — расширенная матрица системы:

Система, имеющая хотя бы одно решение, называется совместной; система, не имеющая ни одного решения — несовместной.
Однородной системой линейных уравнений называется система, правая часть которой равна нулю:
Матричный вид однородной системы: Ax=0.
Однородная система в с е г д а с о в м е с т н а, поскольку любая однородная линейная система имеет по крайней мере одно решение:
Если однородная система имеет единственное решение, то это единственное решение — нулевое, и система называется тривиально совместной. Если же однородная система имеет более одного решения, то среди них есть и ненулевые и в этом случае система называется нетривиально совместной.
Доказано, что при m=n для нетривиальной совместности системы необходимо и достаточно, чтобы определитель матрицы системы был равен нулю.
ПРИМЕР 1. Нетривиальная совместность однородной системы линейных уравнений с квадратной матрицей.
Применив к матрице системы алгоритм гауссова исключения, приведем матрицу системы к ступенчатому виду

Для того, чтобы однородная система была нетривиально совместна, необходимо и достаточно, чтобы ранг r матрицы системы был меньше числа неизвестных n.
ПРИМЕР 2. Нетривиальная совместность однородной системы трех линейных уравнений с четырьмя неизестными.
Исследовать однородную систему — значит установить, является ли она нетривиально совместной, и если является, то найти фундаментальную систему решений и записать выражение для общего решения системы.
Исследуем однородную систему методом Гаусса.
матрица исследуемой однородной системы, ранг которой r
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Совместная, несовместная СЛАУ.
Система называется совместной, или разрешимой, если она имеет по крайней мере одно решение. Система называется несовместной, или неразрешимой, если она не имеет решений.
Определённая, неопределённая СЛАУ.
Если СЛАУ имеет решение и при том единственное, то её называют определённой а если решение неединственное – то неопределённой.
МАТРИЧНЫЕ УРАВНЕНИЯ
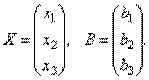
Матрицы дают возможность кратко записать систему линейных уравнений. Пусть дана система из 3-х уравнений с тремя неизвестными:
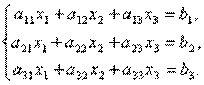
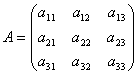
Найдем произведение
т.е. в результате произведения мы получаем левые части уравнений данной системы. Тогда пользуясь определением равенства матриц данную систему можно записать в виде

Здесь матрицы A и B известны, а матрица X неизвестна. Её и нужно найти, т.к. её элементы являются решением данной системы. Это уравнение называют матричным уравнением.
Заметим, что поскольку обратную матрицу можно найти только для квадратных матриц, то матричным методом можно решать только те системы, в которых число уравнений совпадает с числом неизвестных.
Формулы Крамера
Метод Крамера состоит в том, что мы последовательно находим главный определитель системы, т.е. определитель матрицы А : D = det (ai j) и n вспомогательных определителей D i (i= 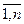
Формулы Крамера имеют вид: D × x i = D i (i = 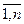
Из этого следует правило Крамера, которое дает исчерпывающий ответ на вопрос о совместности системы: если главный определитель системы отличен от нуля, то система имеет единственное решение, определяемое по формулам: x i = D i / D.
Если главный определитель системы D и все вспомогательные определители D i = 0 (i= 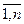
Теорема (правило Крамера): Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём
Доказательство: Итак, рассмотрим систему 3-х уравнений с тремя неизвестными. Умножим 1-ое уравнение системы на алгебраическое дополнение A11 элемента a11, 2-ое уравнение – на A21 и 3-е – на A31:
Сложим эти уравнения:
Рассмотрим каждую из скобок и правую часть этого уравнения. По теореме о разложении определителя по элементам 1-го столбца 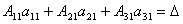
Далее рассмотрим коэффициенты при x2:
Аналогично можно показать, что и 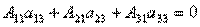
Наконец несложно заметить, что
Таким образом, получаем равенство: 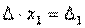
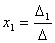
Аналогично выводятся равенства 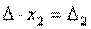

Система линейных уравнений является совместной тогда и только тогда, когда ранг матрицы системы 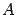
Доказательство: Оно распадается на два этапа.
1. Пусть система имеет решение. Покажем, что 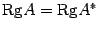
Пусть набор чисел 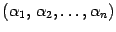


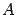


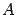
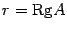

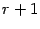
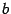
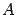
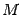
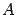


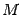



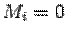

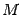

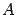

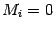

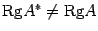
2. Пусть 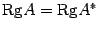
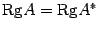
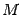
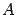
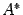
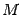
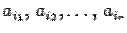
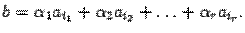 | (1) |
Положим 
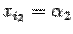

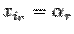
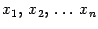
В силу равенства (1) 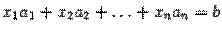

В рассмотренной выше системе 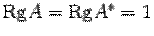


Замечание:Хотя теорема Кронекера-Капелли дает возможность определить, является ли система совместной, применяется она довольно редко, в основном в теоретических исследованиях. Причина заключается в том, что вычисления, выполняемые при нахождении ранга матрицы, в основном совпадают с вычислениями при нахождении решения системы. Поэтому, обычно вместо того, чтобы находить 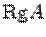
Алгоритм нахождения решений произвольной системы линейных уравнений (метод Гаусса)
Пусть дана система 

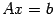
Выпишем расширенную матрицу системы
Назовем элементарными операциями следующие действия с матрицами:
1. перестановка строк;
2. умножение строки на число, отличное от нуля;
3. сложение строки с другой строкой, умноженной на число.
Отметим, что при решении системы уравнений, в отличие от вычисления определителя и нахождения ранга, нельзя оперировать со столбцами. Если по матрице, полученной из 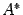
Шаг алгоритма заключается в следующем. Находим первый ненулевой столбец в матрице 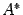

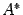

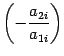
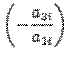
(Первые нулевые столбцы, как правило, отсутствуют.)
Если в матрице 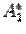
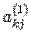
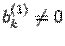
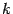
Этому уравнению не удовлетворяет ни один набор чисел 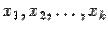
Матрицу 
По отношению к матрице 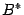
где 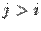
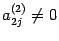
и к матрице 
Процесс останавливается, если после выполнения очередного шага новая уменьшенная матрица состоит из одних нулей или если исчерпаны все строки. Заметим, что заключение о несовместности системы могло остановить процесс и ранее.
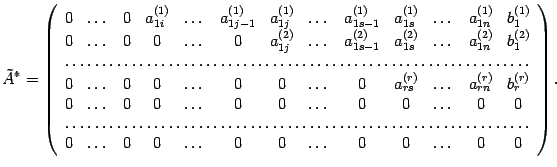
Если бы мы не уменьшали матрицу, то в итоге пришли бы к матрице вида
Далее выполняется так называемый обратный ход метода Гаусса. По матрице 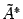

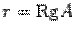
Теперь, придавая неизвестным в правой части произвольные значения и вычисляя значения переменных левой части, мы будем находить различные решения исходной системы Ax=b. Чтобы записать общее решение, нужно неизвестные в правой части обозначить в каком-либо порядке буквами 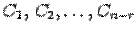
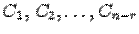
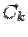
Если система была однородной, то получим общее решение однородной системы. Коэффициенты при 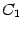

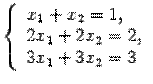 |
имеет решение 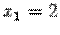
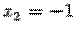
 |
решений не имеет, то есть является несовместной.
Определение: Расширенной матрицей системы линейных уравнений называется матрица 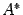
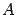
Следствие: Ранг расширенной матрицы 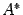
Доказательство: Так как любая линейно независимая система столбцов матрицы A является линейно независимой системой столбцов матрицы 

Квадратные системы с невырожденной матрицей.
Решение СЛАУ:Пусть дана СЛАУ


Данная система всегда совместна так как имеет тривиальное решение х1=…=хn=0
Для существования нетривиальных решений необходимо и достаточно выполнение
Любая совокупность (n-r) линейно независимых решений СЛАУ (являющаяся базисом в пространстве решений) называется фундаментальной совокупностью решений(ФСР).
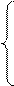
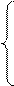
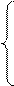
Определив значения базисных переменных, соответствующие каждому набору значений свободных переменных, получим решения:
Х (1) = 


Построенная таким образом система решений системы уравнений называется нормальнойфундаментальной совокупностью решений.
Теорема. Множество всех решений однородной системы уравнений