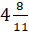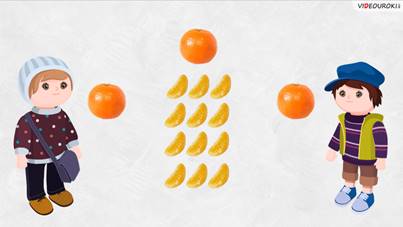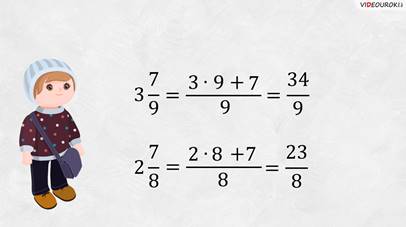что значит смешанное число
Смешанные числа
Так можно записать любую неправильную дробь, у которой числитель не делится на знаменатель.
Дробная часть смешанного числа − это правильная дробь.
Научимся записывать неправильную дробь в виде смешанного числа, т.е. выделять (находить) его целую и дробные части.
Заметим, что число 4 и есть ццелая часть смешанного числа, а число 2 − числитель его дробной части.
Чтобы неправильную дробь, числитель которой нацело не делится на знаменатель, преобразовать в смешанное число, надо числитель разделить на знаменатель; полученное неполное частное записать как целую часть смешанного числа, а остаток − как числитель его дробной части.
Любую неправильную дробь, у которой числитель нацело делится на знаемнатель, можно представить в виде смешанного числа.
Решение. Разделим числитель дроби на знаменатель:
Чтобы преобразовать смешанное число в неправильную дробь, надо целую часьт числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в ее знаемнатель записать знаменатель дробной части смешанного числа.
Отметим, что свойства сложения натуральных чисел выполняются и для дробных чисел:
a + b = b + a − переместительное свойство сложения,
(a + b) + c = a + (b + c) − сочетательное свойство сложения.
Чтобы сложить два смешанных числа, надо отдельно сложить их целые и дробные части.
Научимся вычитать смешанные числа, дробные части котрых имеют равные знаменатели. Если дробная часть уменьшаемого больше или равна дробной части вычитаемого, то можно восспользоваться следующим правилом.
Чтобы найти разность двух смешанных чисел, надо из целой и дробной частей уменьшаемого вычесть соответственно целую и дробную части вычитаемого.
Урок 38 Бесплатно Смешанные числа
На данном уроке мы продолжим разговор об обыкновенных дробях.
Выясним, какие числа называют смешанными, как их принято записывать и читать.
Установим связь между смешанными числами и правильными дробями.
Научимся переводить смешанное число в неправильную дробь.
Рассмотрим обратную операцию перевода неправильной дроби в смешанное число.
Определим расположение смешанных чисел на координатном луче.
Взаимосвязь между смешанным числом и неправильной дробью
Правильной называют дробь, в которой числитель меньше знаменателя, она всегда меньше единицы.
Неправильной называют дробь, в которой числитель больше знаменателя или равен ему, такие дроби всегда больше единицы.
Сегодня речь пойдет о неправильных дробях.
Рассмотрим несколько примеров.
Пример №1.
Разделили три конфеты на троих человек.
Сколько конфет получил каждый?
Известно, что обыкновенная дробь \(\mathbf<\frac
Общее количество конфет (m = 3) разделим на количество человек (n = 3).
Запишем частное в виде дроби.
В результате получили неправильную дробь, в которой числитель равен знаменателю.
\(\mathbf<\frac<3> <3>= 3 \div 3 = 1>\) (конф.) получил каждый.
Ответ: каждый получил 1 конфету.
Пример №2.
Разделили поровну шесть конфет между тремя друзьями.
Сколько конфет получил каждый?
Общее количество конфет (m = 6) разделим на количество друзей (n = 3).
Запишем частное в виде дроби.
В итоге получилась неправильная дробь, в которой числитель больше знаменателя.
\(\mathbf<\frac<6> <3>= 6 \div 3 = 2>\) (конф.) получил каждый из друзей.
Ответ: по 2 конфеты получил каждый из друзей.
В рассмотренных примерах частное двух чисел найти было нетрудно, так как числитель дроби нацело делится на знаменатель.
Рассмотрим еще одну ситуацию.
Пример №3.
Два брата решили разделить поровну пять апельсинов.
Сколько апельсинов достанется каждому из братьев?
Общее количество апельсинов (m = 5) разделим на количество братьев (n = 2).
Запишем частное в виде дроби.
В данном примере мы получили неправильную дробь, в которой числитель хоть и больше знаменателя, но он не делится нацело.
Разделить пять апельсинов на две равные части можно двумя способами.
1. Можно разрезать каждый апельсин на две равные части.
Каждая полученная часть будет равна ½ апельсина.
Тогда по одной части от каждого апельсина достанется каждому из братьев.
Оба мальчика получат по пять таких частей: \(\mathbf<\frac<1> <2>+ \frac<1> <2>+ \frac<1> <2>+ \frac<1> <2>+ \frac<1><2>>\)
Следовательно, каждый получит \(\mathbf<\frac<5><2>>\) апельсина.
Если внимательно присмотреться к сумме дробей, можно заметить, что две части, т.е. сумма \(\mathbf<\frac<1> <2>+ \frac<1><2>>\) составляет \(\mathbf<\frac<2><2>>\).
В свою очередь нам известно, что неправильная дробь \(\mathbf<\frac<2><2>>\) равна единице: \(\mathbf<\frac<2> <2>= 2 \div 2 = 1>\).
Таким образом получится, что каждому мальчику достанется два апельсина, да еще половинка: \(\mathbf<2 + \frac<1><2>>\) апельсина.
2. Можно поделить поровну сначала целые апельсины.
В таком случае каждому брату достанется по два апельсина.
Затем оставшийся апельсин необходимо разделить поровну на двоих, так каждый получит еще по половине апельсина, т.е. (\(\mathbf<\frac<1><2>>\)) его часть.
В результате оба брата получат по два целых апельсина, да еще половину: \(\mathbf<2 + \frac<1><2>>\) апельсина.
Сумму \(\mathbf
Такую сокращенную запись называют смешанным числом, оно имеет целую часть (натуральное число) и дробную часть (дробное число).
Дробная часть смешанного числа- это всегда правильная дробь.
Например, представим смешанные числа в виде суммы их целой и дробной части.
\(\mathbf<1\frac<4> <11>= 1 + \frac<4><11>>\) (целая часть равна 1, дробная- \(\mathbf<\frac<4><11>>\)).
\(\mathbf<7\frac<10> <15>= 7 + \frac<10><15>>\) (целая часть равна 7, дробная- \(\mathbf<\frac<10><15>>\)).
\(\mathbf<\frac<5> <16>= 0 + \frac<5><16>>\) (целая часть отсутствует, т.е. равна 0, дробная- \(\mathbf<\frac<5><16>>\)).
А теперь наоборот сумму натурального числа и правильной дроби представим в виде смешанного числа.
Выразим в килограммах 3 килограмма 150 граммов.
Известно, что 1 кг = 1000 г.
Значит 150 г- это часть от килограмма, т.е. часть от 1000 г.
Чтобы узнать какую часть составляет 150 г от 1000 г, необходимо 150 разделить на 1000, получим \(\mathbf<\frac<150><1000>>\).
В итоге имеем 3 килограмма, да еще часть- \(\mathbf<\frac<150><1000>>\) килограмма, получаем \(\mathbf<3 + \frac<150><1000>>\).
Ответ: 3 килограмма 150 граммов- это \(\mathbf<3\frac<150><1000>>\) килограмма.
Число, содержащее целую часть (натуральное число) и дробную часть (правильную дробь), называют смешанным числом.
Читают смешанное число следующим образом: произносится сначала целая часть, затем дробная, в соответствии с правилами чтения дробных чисел.
В нашем примере про апельсины выражение \(\mathbf<2 + \frac<1><2>>\) можно записать как \(\mathbf<2\frac<1><2>>\).
Число 2— это целая часть смешанного числа, а число \(\mathbf<\frac<1><2>>\) его дробная часть.
Читается данное число так: «Две целых одна вторая».
Любое смешанное число можно перевести в неправильную дробь.
Выясним взаимосвязь смешанных чисел и неправильных дробей на примере.
Испекли три одинаковые пиццы.
От первой пиццы съели несколько кусочков, в результате от нее осталась часть, равная \(\mathbf<\frac<5><8>>\) всей пиццы.
По сути осталось несъеденными 2 (две) целых да еще \(\mathbf<\frac<5><8>>\) (пять восьмых) пиццы.
Если мы сложим эти два числа, то получим сумму \(\mathbf<2 + \frac<5><8>>\).
Выражение \(\mathbf<2 + \frac<5><8>>\) представляет собой ничто иное, как смешанное число \(\mathbf<2\frac<5><8>>\) (две целых пять восьмых).
Общее количество оставшейся пиццы мы можем определить иначе.
Возьмем так же три одинаковые пиццы и разрежем каждую на восемь равных частей.
Теперь вторую и третью пиццу мы можем представить в виде дроби \(\mathbf<\frac<8><8>>\), а остаток от первой запишем как \(\mathbf<\frac<5><8>>\).
В результате общее количество несъеденной пиццы будет выражаться суммой:
При этом ясно, что общее количество оставшейся пиццы, найденное первым способом и вторым, совпадают, значит \(\mathbf<2\frac<5> <8>= \frac<21><8>>\).
Запишем алгоритм перевода смешанного числа в неправильную дробь.
Чтобы представить смешанное число в виде неправильной дроби, необходимо:
1. Умножить целую часть смешанного числа на знаменатель его дробной части.
2. К полученному произведению прибавить числитель дробной части.
3. Записать полученный результат суммы в числитель новой дроби.
4. Знаменатель оставить без изменений.
У меня есть дополнительная информация к этой части урока!
В буквенном виде перевод смешанного числа в неправильную дробь можно записать следующим образом:
Пусть А— целя часть смешанного числа.
\(\mathbf<\frac
Рассмотрим несколько примеров.
Пример №1.
Представьте смешанное число \(\mathbf<6\frac<2><5>>\) в виде дроби.
1. Умножим целую часть смешанного числа (число 6) на знаменатель его дробной части (число 5), получим число 30.
6 • 5 = 30
2. К полученному произведению (число 30) прибавим числитель дробной части смешанного числа (число 2), получим число 32.
3. Запишем полученную сумму (число 32) в числитель новой дроби, а знаменатель останется прежним (число 5).
Получили неправильную дробь \(\mathbf<\frac<32><5>>\).
Пример №2.
Представьте смешанное число \(\mathbf<20\frac<1><3>>\) в виде дроби.
Умножим целую часть смешанного числа на знаменатель его дробной части, к полученному произведению прибавим числитель дробной части, запишем полученный результат суммы в числитель новой дроби, а знаменатель оставим без изменений.
Получили неправильную дробь \(\mathbf<\frac<61><3>>\).
Пример №3.
Представьте смешанное число \(\mathbf<3\frac<3><4>>\) в виде дроби.
Умножим целую часть смешанного числа на знаменатель его дробной части, к полученному произведению прибавим числитель дробной части, запишем полученный результат суммы в числитель новой дроби, а знаменатель оставим без изменений.
Получили неправильную дробь \(\mathbf<\frac<15><4>>\).
Возможна и обратная операция.
Неправильную дробь, в которой числитель нацело не делится на знаменатель, можно представить в виде смешанного числа.
Чтобы перейти от неправильной дроби к смешенному числу, необходимо выделить целую часть.
Выделить целую часть из неправильной дроби- это значит заменить неправильную дробь равным ей смешанным числом.
Для этого необходимо разделить с остатком числитель неправильной дроби на знаменатель.
При этом неполное частное будет являться целой частью, остаток- числителем, а делитель- знаменателем.
Знаменатель неправильной дроби всегда равен знаменателю дробной части смешенного числа.
Запишем алгоритм выделения целой части из неправильной дроби.
Чтобы перейти от неправильной дроби к смешанному числу, необходимо:
1. Разделить с остатком числитель неправильной дроби на ее знаменатель.
2. Неполное частное будет представлять собой целую часть смешанного числа.
3. Если остаток есть, то его необходимо записать в числитель дробной части смешанного числа, а делитель в знаменатель.
У меня есть дополнительная информация к этой части урока!
На примере рассмотрим перевод неправильной дроби в смешанное число.
Выделим целую часть из неправильной дроби \(\mathbf<\frac<37><8>>\).
Давайте выполним деление с остатком в столбик («деление уголком»).
Наибольшее число, которое меньше 37 и делится на 8— это 32.
32 разделим на делитель 8, получим 4-это неполное частное.
Вычтем из делимого числа 37 найденное наибольшее число 32, получим число 5— это остаток от деления.
По-другому деление с остатком можно записать так 37 ÷ 8 = 4 ( ост. 5 ).
В результате получим смешанное число \(\mathbf<4\frac<5><8>>\), в котором 4— целая часть, \(\mathbf<\frac<5><8>>\)- дробная часть.
Пройти тест и получить оценку можно после входа или регистрации
Смешанные числа на координатном луче
Выясним, где на координатном луче находятся смешанные числа.
1. Для того чтобы изобразить на координатном луче смешанное число, важно выбрать правильно длину единичного отрезка.
Единичный отрезок целесообразно устанавливать такой длины, чтобы было удобно его разделить на части, количество которых должно соответствовать числу, стоящему в знаменателе.
2. Далее от начала отсчета нужно отложить определенное количество равных частей, соответствующих числу, стоящему в числителе.
Рассмотрим поясняющий пример.
Отметим на координатном луче точку с координатой \(\mathbf<2\frac<2><3>>\).
\(\mathbf<2\frac<2><3>>\)— это смешанное число.
Данное смешанное число содержит правильную дробь со знаменателем 3.
Следовательно, единичный отрезок разобьем на три равные части, каждая такая часть (доля) будет равна \(\mathbf<\frac<1><3>>\) единичного отрезка.
Изобразим горизонтальный координатный луч, направленный вправо, с началом отсчета в точке О(0) и единичным отрезком ОЕ, равным 1 единице.
В таком случае одна часть (доля единичного отрезка) соответствует дроби \(\mathbf<\frac<1><3>>\), две части- это \(\mathbf<\frac<2><3>>\), три части- это 1.
Чтобы изобразить смешанное число \(\mathbf<2\frac<2><3>>\), отсчитываем от начала координат два целых единичных отрезка, а от третьего единичного отрезка возьмем только две его доли из трех.
Отметим точку на координатном луче, назовем ее точка А(\(\mathbf<2\frac<2><3>>\)).
Переведем смешанное число в неправильную дробь.
Определим расположение точки с координатой \(\mathbf<\frac<8><3>>\).
Дробь \(\mathbf<\frac<8><3>>\) означает восемь долей единичного отрезка ОЕ.
Отложим от начала координат восемь долей, каждая из которых равна \(\mathbf<\frac<1><3>>\) единичного отрезка.
Попадем в точку с координатой \(\mathbf<\frac<8><3>>\).
В этой же точке мы ранее отметили точку А(\(\mathbf<2\frac<2><3>>\)).
Смешанное число и соответствующая ему неправильная дробь, у которой числитель больше знаменателя, на координатном луче находятся всегда правее единицы и принадлежат они одной и той же точке координатного луча.
Определим расположение точек В(\(\mathbf<1\frac<2><3>>\)), С(\(\mathbf<2\frac<1><3>>\)), D(\(\mathbf<\frac<12><3>>\)) на координатном луче.
Изобразим горизонтальный координатный луч, направленный вправо, с началом отсчета в точке О(0) и единичным отрезком ОЕ, равным 1 единице.
Так как знаменатель каждой заданной дроби равен трем, то разобьем единичный отрезок ОЕ на три равные части, каждая часть будет равна \(\mathbf<\frac<1><3>>\) ОЕ.
1. Смешанное число \(\mathbf<1\frac<2><3>>\) представляет собой один целый единичный отрезок, да еще две части (доли) из трех от второго единичного отрезка.
Следовательно, точка В(\(\mathbf<1\frac<2><3>>\)) будет удалена вправо от начала координат на расстояние одного целого единичного отрезка, да еще двух отрезков, каждый из которых равен одной доле единичного отрезка.
В данную точку также мы можем попасть, если от начала координат вправо отсчитаем пять долей единичного отрезка- (\(\mathbf<\frac<5><3>>\))ОЕ.
Таким образом точка с координатой \(\mathbf<\frac<5><3>>\) и точка с координатой \(\mathbf<1\frac<2><3>>\) это одна и та же точка на координатном луче.
Отметим тот факт, что \(\mathbf<1\frac<2><3>>\) смешанное число и соответствующая ему неправильная дробь \(\mathbf<\frac<5><3>>\) больше единицы, и на координатном луче данные точки располагаются правее единицы (правее точки E(1)).
2. Выясним, где на координатном луче будет находиться точка С(\(\mathbf<2\frac<1><3>>\)).
Смешанное число \(\mathbf<2\frac<1><3>>\) представляет собой два целых единичных отрезка, да еще одну часть (долю) из трех от третьего единичного отрезка.
Отметим точку С(\(\mathbf<2\frac<1><3>>\)) на координатном луче, для этого отсчитаем вправо от начала координат два целых единичных отрезка и еще одну долю единичного отрезка, равную \(\mathbf<\frac<1><3>>\) ОЕ.
Так же в данную точку можно попасть, если от начала координат вправо отсчитать семь долей единичного отрезка- (\(\mathbf<\frac<7><3>>\))OE.
Точка с координатой \(\mathbf<\frac<7><3>>\) и точка с координатой \(\mathbf<2\frac<1><3>>\) это одна и та же точка на координатном луче.
Смешанное число \(\mathbf<2\frac<1><3>>\) и соответствующая ему неправильная дробь \(\mathbf<\frac<7><3>>\) больше единицы, на координатном луче данные точки располагается правее единицы (правее точки E(1)) и правее найденной нами точки В(\(\mathbf<1\frac<2><3>>\)).
3. Обозначим на координатном луче точку D с координатой \(\mathbf<\frac<12><3>>\).
\(\mathbf<\frac<12><3>>\)- неправильная дробь, в которой числитель больше знаменателя.
Найдем соответствующее этой дроби смешанное число, для этого выделим из дроби \(\mathbf<\frac<12><3>>\) целую часть.
Получается, что дробь \(\mathbf<\frac<12><3>>\) равна четырем целым единичным отрезкам.
Дробная часть данного числа отсутствует, т.е. она равна нулю.
\(\mathbf<\frac<12><3>>\) и 4— это одно и то же число, значит \(\mathbf<\frac<12> <3>= 4>\).
Отложим от начала координат четыре целых единичных отрезка и обозначим точку D(\(\mathbf<\frac<12><3>>\)).
Обратите внимание как расположены смешанные числа на координатном луче, чем правее от единицы находится смешанное число, тем оно больше.
Пройти тест и получить оценку можно после входа или регистрации
Смешанные числа
Урок 29. Математика 5 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Смешанные числа»
– Паша, привет. Хочешь мандарин?
– Привет, Саша. Да, хочу. Я очень люблю мандарины.
– Смотри, у меня 3 мандарина, нас двое. Надо как-то эти мандарины разделить.
– Давай почистим все мандарины, посчитаем, сколько всего долек, и поделим их на 2.
– Давай. Смотри, в каждом мандарине 12 долек. У нас 3 мандарина, значит, и долек 36. Каждому получается по 18 долек.
– Подожди, Саша. Но мы можем же мандарины поделить и по-другому. Взять каждый по одному, а третий мандарин разделить пополам. В нём 12 долек, значит, каждый получит по 1 целому мандарину и по 6 долек.
– Ты прав, Паша. И как тогда записать? Если мы берём по 18 долек, то можем это записать как 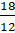
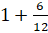
– Ничего не понимаю. Давай пойдём к Электроше. Он точно нам поможет разобраться.
– Электроша, привет. Смотри, мы попробовали разделить на двоих 3 мандарина и у нас что-то не очень понятное получилось. Если сначала мандарины разделить на дольки и делить их, то получится, что каждый из нас должен взять 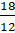
– Успокойтесь, ребята. Сейчас мы с вами во всём разберёмся, но сначала давайте устно выполним несколько упражнений.
Вернёмся к вашей задаче.
Запишем дробь 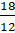
– Конечно, Электроша, помню. Числитель этой дроби больше знаменателя, значит, перед нами неправильная дробь.
Давайте подумаем, суммой каких дробей её можно представить?
– Ну, например, 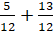
– Или 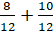
Мы можем ещё долго перечислять.
– Да, мальчики, вы правильные суммы называете. А давайте запишем 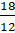
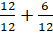
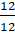
– Числитель равен знаменателю, значит, эта дробь равна 1. То есть нашу дробь можно записать так: 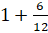
– А 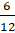
– Числитель меньше знаменателя, значит, это правильная дробь.
– Ой, – удивился Саша, – так у нас же получилось то же самое, когда мы сначала взяли себе по целому мандарину, а потом оставшийся мандарин поделили пополам.
– Конечно, Саша. У вас и должно было так получиться.
У нас получилось, что неправильную дробь мы представили в виде суммы натурального числа и правильной дроби.
Давайте посмотрим, может, это только дробь 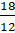
Возьмём дробь 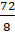
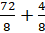
Чему равна дробь 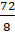
– Конечно. Эта дробь равна 9. Тогда получим, что дробь 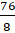
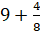
Опять получилась сумма натурального числа и правильной дроби. Так что получается, Электроша? Любую неправильную дробь можно представить в виде такой суммы?
– Да, запомните правило: любую неправильную дробь, у которой числитель не делится нацело на знаменатель, можно представить в виде суммы натурального числа и правильной дроби.
Обратите внимание на слова «числитель не делится нацело на знаменатель». Если же числитель делится нацело на знаменатель, например, дробь 
Но вернёмся к нашим примерам. Как правило, такие суммы записывают так 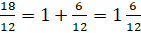
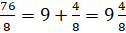
Числа такого вида называют смешанными числами. Ну, почему такое название, я думаю, вам понятно.
– Да, Электроша, ясно. Смешали натуральные числа и дробные, вот и получились смешанные числа.
– Да, Саша, ты прав. У каждого компонента смешанной дроби есть своё название.
Так, натуральное число называют целой частью смешанного числа, а дробь – дробной частью смешанного числа.
Обратите внимание, дробная часть смешанного числа – это обязательно правильная дробь.
Например, число 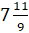
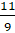
– Всё понятно, Электроша. А дай нам задание, чтобы проверить, как мы поняли, что такое смешанные числа.
Среди предложенных чисел 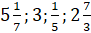
– 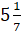
Число 3 несмешанное, так как у него нет дробной части.

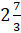
Сейчас мы с вами научимся переводить неправильную дробь в смешанное число.
То есть разберём то, как правильно выделять или, другими словами, находить целую и дробную части числа.
Давайте посмотрим на дробь 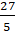
Выполним деление с остатком числа 27 на 5.
Получим, что 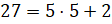
– Ну как, мальчики, вы всё поняли?
– Вроде бы, да. Но давай решим какое-нибудь задание, чтобы нам стало ещё яснее.
Вот задание для тебя, Саша.
Переведите неправильные дроби в смешанные числа 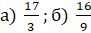
Первая дробь – 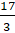
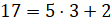
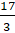
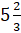
– Я так понял, Электроша?
– Да, Саша. Ты всё правильно понял. Продолжай.
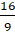
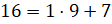
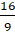
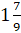
Запомните правило: для того, чтобы неправильную дробь, у которой числитель не делится нацело на знаменатель, преобразовать в смешанное число, надо числитель разделить на знаменатель.
Полученное неполное частное записывается как целая часть смешанного числа, а остаток – как числитель дробной части смешанного числа.
Знаменатель дробной части будет равен знаменателю неправильной дроби.
Теперь давайте вернёмся к предыдущему правилу и немного его исправим. Теперь можно записать так: любую неправильную дробь, у которой числитель нацело не делится на знаменатель, можно представить в виде смешанного числа.
Ну что, вам стало понятно, что такое смешанные числа и как неправильные дроби в них переводить?
– Да, это понятно. Но вот интересно, а смешанное число можно перевести в неправильную дробь?
Давайте возьмём, например, число 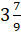
Представим это число в виде суммы 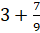
Мы помним, что любое натуральное число можно представить в виде дроби с любым знаменателем. Представим 3 в виде дроби со знаменателем 9. Получим, что смешанное число равно 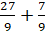
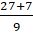
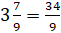
Попробуй, Саша, перевести число 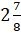
– Представим это число в виде суммы 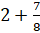
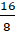
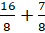
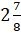
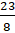
Есть правило, которое помогает упростить перевод смешанного числа в неправильную дробь.
Для того, чтобы преобразовать смешанное число в неправильную дробь, надо целую часть числа умножить на знаменатель дробной части. К полученному произведению надо добавить числитель дробной части. Эту сумму записать как числитель неправильной дроби, а в её знаменатель записать знаменатель дробной части смешанного числа.
Вернёмся к нашим примерам и попробуем перевести смешанное число в дробь по этому правилу 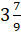
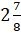
Начнём с 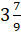
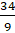
Попробуй, Паша, перевести этим способом в дробь число 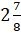
– Умножим 2 на 8 и добавим 7. Получим, что числитель неправильной дроби будет равен 23. А знаменатель – 8. 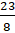
Выполните такое задание.
Преобразуйте смешанные числа в дроби, а неправильные дроби – в смешанные числа 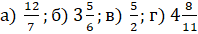
– Итак, дробь 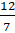
Разделим 12 на 7 с остатком. Получим 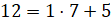
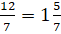
Переведём 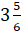
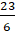
– Теперь, Паша, продолжи решать ты.
Дробь 
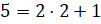
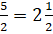
Для того, чтобы перевести число