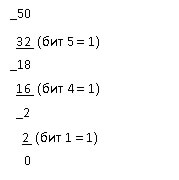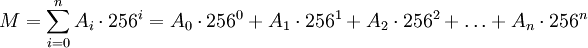что значит старший и младший байт

Русские Блоги

О сетевом порядке байтов

Исходный адрес:https://blog.csdn.net/erlib/article/details/8937068
В последние несколько дней я снова начал создавать сетевые приложения. Так как это сетевое программирование, порядок байтов должен быть важным элементом знаний, о котором следует помнить. Разместите статью как напоминание!

Различные процессоры имеют разные типы байтов. Эти порядки байтов относятся к порядку, в котором целые числа хранятся в памяти. Это называется порядком узлов.
Есть два наиболее распространенных
1. Little endian: храните младший байт в начальном адресе
2. Big endian: хранить старший байт в начальном адресе

LE little-endian

BE big-endian

Самый интуитивный порядок байтов
Младший бит адреса хранит старший бит значения.
Младший бит значения хранения старшего бита адреса
Почему это интуитивно понятно, не учитывайте соответствие
нужно только записать адрес памяти слева направо в порядке от меньшего к большему.
Запишите значение в обычном порядке от большего к меньшему.
Сравните два, заполняйте по одному байту

Для преобразования сокет bsd предоставляет следующие четыре функции преобразования:

В системах с прямым порядком байтов эти функции преобразуют порядок байтов.
В системах с прямым порядком байтов эти функции будут определены как пустые макросы.

Точно так же при разработке сетевых программ или кроссплатформенной разработке вы также должны обращать внимание на использование только одного порядка байтов, иначе интерпретация двух сторон будет разной и возникнут ошибки.

Заметка:

Один, определение порядка байтов

Фактически, большинство людей редко имеют дело непосредственно с порядком байтов в процессе разработки. Только в кроссплатформенных и сетевых программах следует учитывать порядок байтов.

Во всех статьях о порядке байтов будет упоминаться, что порядок байтов делится на две категории: Big-Endian и Little-Endian. Определения Big-Endian и Little-Endian, которые цитируют стандарт, следующие:
a) Little-Endian означает, что младший байт помещается в конец младшего адреса памяти, а старший байт помещается в конец старшего адреса памяти.
б) Big-Endian означает, что старший байт помещается в конец младшего адреса памяти, а младший байт помещается в конец высокого адреса памяти.
c) Сетевой порядок байтов: 4 байта 32-битных значений передаются в следующем порядке: сначала 0 ～ 7 бит, затем 8 ～ 15 бит, затем 16 ～ 23 бит и, наконец, 24

2. Старший / младший адрес, старший и младший байты

Прежде всего, нам нужно знать структуру пространства памяти в нашем образе программы C: есть инструкции по структуре пространства памяти в «C Expert Programming» или «Unix Environment Advanced Programming», примерно следующим образом:

И старший и младший адреса, и старший и младший байты очищены. Давайте еще раз рассмотрим определение обратного порядка байтов и обратного порядка байтов и проиллюстрируем два порядка байтов с помощью значков:
В качестве примера возьмем значение unsigned int = 0x12345678 и рассмотрим условия хранения в двух степенях порядка байтов соответственно. Мы можем использовать unsigned char buf [4] для представления значения:
Big-Endian: младший адрес хранит старший бит, как показано ниже:

Intel X86 использует Little-Endian на существующих платформах, а SPARC, как Sun, использует Big-Endian.

Три, примеры

Разработчики встроенных систем должны хорошо разбираться в режимах Little-endian и Big-endian. ЦП, использующий режим обратного порядка байтов, сохраняет операнды от младшего байта к старшему, а режим прямого порядка байтов сохраняет операнды от старшего байта к младшему.

Источник

Побитовые или поразрядные операции

Операнды поразрядных операций могут быть любого целого типа. К побитовым, или поразрядным операциям относятся:

Кроме того, рассматриваются операции сдвигов «, ».

Значение старшего, младшего слова(2 байта), бита

Запись многобайтового числа из памяти компьютера в файл или передача по сети требует соблюдения соглашений о том, какой из байтов является старшим, а какой младшим. Прямая запись ячеек памяти приводит к возможным проблемам при переносе приложения с платформы на платформу. Варианты записи: от старшего к младшему или (англ. big-endian, дословно: «тупоконечный»): этот порядок является стандартным для протоколов TCP/IP, он используется в заголовках пакетов данных и во многих протоколах более высокого уровня, разработанных для использования поверх TCP/IP. Поэтому, порядок байтов от старшего к младшему часто называют сетевым порядком байтов (англ. network byte order). От младшего к старшему или (англ. little-endian, дословно: «остроконечный»): запись начинается с младшего и заканчивается старшим. Этот порядок записи принят в памяти персональных компьютеров с x86-процессорами, в связи с чем иногда его называют интеловский порядок байтов.

Чтобы получить значение младщего слова (OWORD)

Операции

потому что только нулевой и четвертый разряды обоих операндов содержат 1.

потому что все разряды (кроме шестого) в одном из двух операндов имеют значение 1.

Заметим, что, поскольку нулевой разряд в обоих операндах имеет значение 1, нулевой разряд результата имеет значение 0.

Описанные выше операции часто используются для установки некоторых битов, причем другие биты остаются неизменными. Они удобны для фильтрации или маскирования битов.

Таким образом, х«2 сдвигает х влево на 2 позиции, заполняя освобождающиеся позиции нулями (эквивалентно умножению на 4).

Для значений без знака имеем

Эти две операции выполняют сдвиг, а также эффективное умножение и деление на степени числа 2.

Комментарии к коду.

Побитовые операторы JavaScript

Для понимания побитовых операторов необходимо свободно уметь работать с двоичным представлением чисел. Если это не так, остается только надеяться, что данные операторы не часто вам будут попадаться в вашей практике. Ниже следует перечень побитовых операторов с примерами их применения (примеры и результаты даны, так же, и в бинарной (двоичной) форме):

Таблица. Побитовые операторы.

Листинг: определение четности числа

Если в результате получится значение false, то заданное число является нечетным, в противном случае, число является четным.

Источник

Разбираемся с прямым и обратным порядком байтов

Числа и данные

Наиболее важная концепция заключается в понимании разницы между числами и данными, которые эти числа представляют. Число — это абстрактное понятия, как исчислитель чего-то. У Вас есть десять пальцев. Понятие “десять” не меняется, в зависимости от использованного представления: десять, 10, diez (испанский), ju (японский), 1010 (бинарное представление), Х (римские числа)… Все эти представления указывают на понятие “десяти”.

Сравним это с данными. Данные — это физическое понятие, просто последовательность битов и байтов, хранящихся на компьютере. Данные не имеют неотъемлемого значения и должны быть интерпретированы тем, кто их считывает.

Данные — это как человеческое письмо, просто набор отметок на бумаге. Этим отметкам не присуще какое-либо значение. Если мы видим линию и круг (например, |O), то можно интерпретировать это как “десять”. Но это лишь предположение, что считанные символы представляют число. Это могут быть буквы “IO” — название спутника Юпитера. Или, возможно, имя греческой богини. Или аббревиатура для ввода/вывода. Или чьи-то инициалы. Или число 2 в бинарном представлении (“10”). Этот список предположений можно продолжить. Дело в том, что один фрагмент данных (|O) может быть интерпретировано по разному, и смысл остается не ясен, пока кто-то не уточнит намерения автора.

Компьютеры сталкиваются с такой же проблемой. Они хранят данные, а не абстрактные понятия, используя при этом 1 и 0. Позднее они считывают эти 1 и 0 и пытаются воссоздать абстрактные понятия из набора данных. В зависимости от сделанных допущений, эти 1 и 0 могут иметь абсолютно разное значение.

Почему так происходит? Ну, вообще-то нет такого правила, что компьютеры должны использовать один и тот же язык, так же, как нет такого правила и для людей. Каждый компьютер одного типа имеет внутреннюю совместимость (он может считывать свои собственные данные), но нет никакой гарантии, как именно интерпретирует эти данные компьютер другого типа.

Храним числа как данные

Так в чем же проблема — компьютеры отлично ладят с одиночными байтами, правда? Ну, все превосходно для однобайтных данных, таких как ASCII-символы. Однако, много данных используют для хранения несколько байтов, например, целые числа или числа с плавающей точкой. И нет никакого соглашения о том, в каком порядке должны хранится эти последовательности.

Пример с байтом

Рассмотрим последовательность из 4 байт. Назовем их W X Y и Z. Я избегаю наименований A B C D, потому что это шестнадцатеричные числа, что может немного запутывать. Итак, каждый байт имеет значение и состоит из 8 бит.

Например, W — это один байт со значением 0х12 в шестнадцатеричном виде или 00010010 в бинарном. Если W будет интерпретироваться как число, то это будет “18” в десятеричной системе (между прочим, ничто не указывает на то, что мы должны интерпретировать этот байт как число — это может быть ASCII-символ или что-то совсем иное). Вы все еще со мной? Мы имеем 4 байта, W X Y и Z, каждый с различным значением.

Понимаем указатели

Указатели являются ключевой частью программирования, особенно в языке С. Указатель представляет собой число, являющееся адресом в памяти. И это зависит только от нас (программистов), как интерпретировать данные по этому адресу.

В языке С, когда вы кастите (приводите) указатель к конкретному типу (такому как char * или int *), это говорит компьютеру, как именно интерпретировать данные по этому адресу. Например, давайте объявим:

Обратите внимание, что мы не можем получить из р данные, потому что мы не знаем их тип. р может указывать на цифру, букву, начало строки, Ваш гороскоп или изображение — мы просто не знаем, сколько байт нам нужно считать и как их интерпретировать.

Теперь предположим, что мы напишем:

Этот оператор говорит компьютеру, что р указывает на то же место, и данные по этому адресу нужно интерпретировать как один символ (1 байт). В этом случае, с будет указывать на память по адресу 0, или на байт W. Если мы выведем с, то получим значение, хранящееся в W, которое равно шестнадцатеричному 0x12 (помните, что W — это полный байт). Этот пример не зависит от типа компьютера — опять же, все компьютеры одинаково хорошо понимают, что же такое один байт (в прошлом это было не всегда так).

Этот пример полезен, он одинаково работает на все компьютерах — если у нас есть указатель на байт (char *, один байт), мы можем проходить по памяти, считывая по одному байту за раз. Мы можем обратиться к любому месту в памяти, и порядок хранения байт не будет иметь никакого значения — любой компьютер вернет нам одинаковую информацию.

Так в чем же проблема?

Проблемы начинаются, когда компьютер пытается считать несколько байт. Многие типы данных состоят больше чем из одного байта, например, длинные целые (long integers) или числа с плавающей точкой. Байт имеет только 256 значений и может хранить числа от 0 до 255.

Повторюсь, порядок следования байтов не имеет значения пока Вы работаете с одним байтом. Если у Вас есть один байт, то это просто данные, которые Вы считываете и есть только один вариант их интерпретации (опять таки, потому что между компьютерами согласовано понятие одного байта).

Теперь предположим, что у нас есть 4 байта (WXYZ), которые хранятся одинаково на машинах с обоими типами порядка записи байтов. То есть, ячейка памяти 0 соответствует W, ячейка 1 соответствует X и т. д.

Мы можем создать такое соглашение, помня, что понятие “байт” является машинно-независимым. Мы можем обойти память по одному байту за раз и установить необходимые значения. Это будет работать на любой машине.

Такой код будет работать на любой машине и успешно установит значение байт W, X, Y и Z расположенных на соответствующих позициях 0, 1, 2 и 3.

Интерпретация данных

Теперь давайте рассмотрим пример с многобайтными данными (наконец-то!). Короткая сводка: “short int” это 2-х байтовое число (16 бит), которое может иметь значение от 0 до 65535 (если оно беззнаковое). Давайте используем его в примере.

Теперь Вы видите проблему? Машина с порядком хранения от старшего к младшему считает, что s = 0x1234, в то время как машина с порядком хранения от младшего к старшему думает, что s = 0x3412. Абсолютно одинаковые данные дают в результате два совершенно разных числа.

И еще один пример

Давайте для “веселья” рассмотрим еще один пример с 4 байтовым целым:

Проблема NUXI

Проблему с порядком байт иногда называют проблемой NUXI: слово UNIX, сохраненное на машинах с порядком хранения от старшего к младшему, будет отображаться как NUXI на машинах с порядком от младшего к старшему.

Допустим, что мы собираемся сохранить 4 байта (U, N, I, и X), как два short int: UN и IX. Каждая буква занимает целый байт, как в случае с WXYZ. Для сохранения двух значений типа short int напишем следующий код:

Этот код не является специфичным для какой-то машины. Если мы сохраним значение “UN” на любой машине и считаем его обратно, то обратно получим тоже “UN”. Вопрос порядка следования байт не будет нас волновать, если мы сохраняем значение на одной машине, то должны получить это же значение при считывании.

Однако, если пройтись по памяти по одному байту за раз (используя трюк с char *), то порядок байт может различаться. На машине с прямым порядком хранения мы увидим:

Что имеет смысл. “U” является старшим байтом в “UN” и соответственно хранится первым. Такая же ситуация для “IX”, где “I” — это старший байт и хранится он первым.

На машине с обратным порядком хранения мы скорее всего увидим:

Но и это тоже имеет смысл. “N” является младшим байтом в “UN” и значит хранится он первым. Опять же, хотя байты хранятся в “обратном порядке” в памяти, машины с порядком хранения от младшего к старшему знают что это обратный порядок байт, и интерпретирует их правильно при чтении. Также, обратите внимание, что мы можем определять шестнадцатеричные числа, такие как 0x1234, на любой машине. Машина с обратным порядком хранения байтов знает, что Вы имеете в виду, когда пишите 0x1234 и не заставит Вас менять значения местами (когда шестнадцатеричное число отправляется на запись, машина понимает что к чему и меняет байты в памяти местами, скрывая это от глаз. Вот такой трюк.).

Рассмотренный нами сценарий называется проблемой “NUXI”, потому что последовательность “UNIX” интерпретируется как “NUXI” на машинах с различным порядком хранения байтов. Опять же, эта проблема возникает только при обмене данными — каждая машина имеет внутреннюю совместимость.

Обмен данными между машинами с различным порядком хранения байтов

Сейчас компьютеры соединены — прошли те времена, когда машинам приходилось беспокоиться только о чтении своих собственных данных. Машинам с различным порядком хранения байтов нужно как-то обмениваться данными и понимать друг друга. Как же они это делают?

Решение 1: Использовать общий формат

Самый простой подход состоит в согласовании с общим форматом для передачи данных по сети. Стандартным сетевым является порядок от старшего к младшему, но некоторые люди могут расстроиться, что не победил порядок от младшего к старшему, поэтому просто назовем его “сетевой порядок”.

Для конвертирования данных в соответствии с сетевым порядком хранения байтов, машины вызывают функцию hton() (host-to-network). На машинах с прямым порядком хранения эта функция не делает ничего, но мы не будем говорить здесь об этом (это может разозлить машины с обратным порядком хранения 🙂 ).

Но важно использовать функцию hton() перед отсылкой данных даже если Вы работаете на машине с порядком хранения от старшего к младшему. Ваша программа может стать весьма популярной и будет скомпилирована на различных машинах, а Вы ведь стремитесь к переносимости своего кода (разве не так?).

Точно также существует функция ntoh() (network-to-host), которая используется для чтения данных из сети. Вы должны использовать ее, чтобы быть уверенными, что правильно интерпретируете сетевые данные в формат хоста. Вы должны знать тип данных, которые принимаете, чтобы расшифровать их правильно. Функции преобразования имеют следующий вид:

Помните, что один байт — это один байт и порядок не имеет значения.

Эти функции имеют критическое значение при выполнении низкоуровневых сетевых операций, таких как проверка контрольной суммы IP-пакетов. Если Вы не понимаете сути проблемы с порядком хранения байтов, то Ваша жизнь будет наполнена болью — поверьте мне на слово. Используйте функции преобразования и знайте, зачем они нужны.

Решение 2: Использования маркера последовательности байтов (Byte Order Mark — BOM)

Этот подход подразумевает использование некого магического числа, например 0xFEFF, перед каждым куском данных. Если Вы считали магическое число и его значение 0xFEFF, значит данные в том же формате, что и у Вашей машины и все хорошо. Если Вы считали магическое число и его значение 0xFFFE, это значит, что данные были записаны в формате, отличающемся от формата вашей машины и Вы должны будете преобразовать их.

Нужно отметить несколько пунктов. Во-первых, число не совсем магическое, как известно программисты часто используют этот термин для описания произвольно выбранных чисел (BOM может быть любой последовательностью различных байтов). Такая пометка называется маркером последовательности байтов потому что показывает в каком порядке данные были сохранены.

Во-вторых, BOM добавляет накладные расходы для всех передаваемых данных. Даже в случае передачи 2 байт информации Вы должны добавлять к ним 2 байта маркера BOM. Пугающе, не так ли?

Unicode использует BOM, когда сохраняет многобайтные данные (некоторые кодировки Unicode могут иметь по 2, 3 и даже 4 байта на символ). XML позволяет избежать этой путаницы, сохраняя данные сразу в UTF-8 по умолчанию, который сохраняет информацию Unicode по одному байту за раз. Почему это так круто?

Повторяю в 56-й раз — потому что проблема порядка хранения не имеет значения для единичных байт.

Опять же, в случае использования BOM может возникнуть другие проблемы. Что, если Вы забудете добавить BOM? Будете предполагать, что данные были отправлены в том же формате, что и Ваши? Прочитаете данные и, увидев что они “перевернуты” (что бы это не значило), попытаетесь преобразовать их? Что, если правильные данные случайно будут содержать неправильный BOM? Эти ситуации не очень приятные.

Почему вообще существует эта проблема? Нельзя ли просто договориться?

Ох, какой же это философский вопрос. Каждый порядок хранения байтов имеет свои преимущества. Машины с порядком следования от младшего к старшему позволяют читать младший байт первым, не считывая при этом остальные. Таким образом можно легко проверить является число нечетным или четным (последний бит 0), что очень здорово, если Вам необходима такая проверка. Машины с порядком от старшего к младшему хранят данные в памяти в привычном для человека виде (слева направо), что упрощает низкоуровневую отладку.

Так почему же все просто не договорятся об использовании одной из систем? Почему одни компьютеры пытаются быть отличными от других? Позвольте мне ответить вопросом на вопрос: почему не все люди говорят на одном языке? Почему в некоторых языках письменность слева направо, а у других справа налево?

Иногда системы развиваются независимо, а в последствии нуждаются во взаимодействии.

Источник

Что значит старший и младший байт

Прежде, чем рассматривать выполнение машинных программ аппаратурой ЭВМ, рассмотрим представление в памяти машины чисел, а также алфавитно-цифровых символов. Это представление потребуется нам в дальнейшем при изучении машинных программ, а также обрабатываемых ими данных.

1.1 Двоичные числа

Чтобы сделать вычислительные системы более надежными и простыми, их аппаратура строится из простейших электронных схем, которые могут находиться только в двух состояниях. Одно из них обозначается 0, а другое – 1. Такая схема предназначена для длительного или краткого хранения самой мелкой единицы информации – бита (от «BInary digiT» – двоичная цифра).

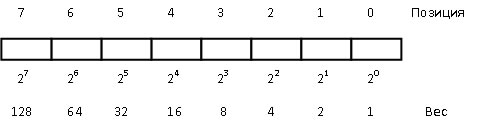
Любое число можно представить в виде цепочки битов. Такое представление числа называется двоичным числом. Цепочка из восьми битов называется байтом (рис. 1).

старший бит (бит 7) младший бит (бит 0)

Рис. 1. Пример байта

Величина двоичного числа определяется относительной позицией каждого бита и его значением. Позиционный вес младшего бита 2 о = 1(10), где 1(10) – единица в десятичной системе счисления. Следующий бит имеет вес 2 1 = 2(10). Вес любой позиции получается удвоением веса предыдущей позиции (рис. 2).

Рис. 2. Веса позиций байта

Для преобразования десятичного числа в двоичное можно использовать один из двух методов – метод деления и метод вычитания. Первый из этих методов широко используется в программах, выполняющих преобразование чисел из одной системы счисления в другую. Этот метод будет рассмотрен нами в других разделах, при описании соответствующих программ. Сейчас мы будем использовать метод вычитания, главное достоинство которого – наглядность. Согласно этому методу, для преобразования десятичного числа в двоичное надо сделать ряд вычитаний, каждое из которых даст значение одного бита.

Записывая 0 в остальные позиции битов (биты 0,2,3) получаем окончательный результат: 110010.

Для выполнения обратного преобразования следует сложить десятичные веса тех позиций, в которых стоит 1:

32 (бит 5) + 16 (бит 4) + 2 (бит 1) = 50

Байт может представлять десятичные положительные числа от 0 (00000000) до 255 (11111111). Число 255 может быть получено двумя способами: 1) суммированием весов всех битов байта; 2) по формуле 2 8 – 1, где 8 – номер первого бита, не вошедшего в состав байта.

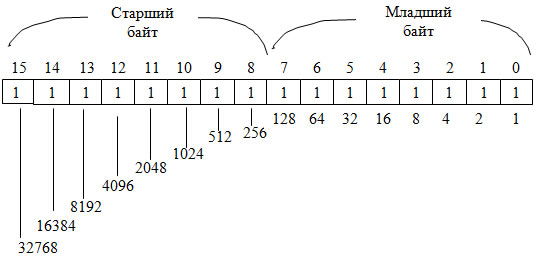
Машинным словом будем называть битовую строку длиной 16 битов. Одно слово содержит 2 байта (рис. 3). Каждый бит слова имеет свой вес. Просуммировав все веса, найдем максимальное целое число без знака, которое можно записать в одно слово, оно равно 2 16 – 1 = 65535.

Двоичное содержимое байта или слова может рассматриваться (интерпретироваться) как число без знака и как число со знаком. Число без знака занимает все 16 битов слова или 8 битов байта. Оно может быть только положительным. Просуммируем два таких числа:

Обратим внимание, что единица, появившаяся в старшем бите результата, свидетельствует лишь о возросшей величине результата, который для беззнаковых чисел может быть только неотрицательным.

Рис. 3. Веса позиций слова

все биты числа (в том числе и знаковый) инвертируются;

к полученному числу прибавляется 1.

Например, получим дополнительный код числа –65:

Для получения абсолютного значения отрицательного числа повторяют эти же самые два действия. Например:

Сумма +65 и –65 должна составить ноль:

В данном примере у нас произошли два интересных переноса: 1) в знаковый (7-й) разряд; 2) за пределы байта. Первая единица переноса обрабатывается как обычно, а вторая теряется. Оба переноса считаются правильными.

Отсюда видно, что нулевые биты в отрицательном двоичном числе фактически определяют его величину: рассмотрите весовые значения нулевых битов так, как если бы это были единичные биты, сложите эти значения и прибавьте 1.

Источник

Порядок байт

Поря́док ба́йтов в информатике — метод записи байтов многобайтовых чисел.

В общем случае, когда нужно компактно записать число, большее 255 ( 2 8 − 1 = 255 — максимальное целое число, записываемое одним байтом (октетом)) необходимо использовать несколько байтов. Число M факторизуется по основанию 256:

Набор чисел и является последовательностью байтов для записи.

Содержание

Варианты записи

Порядок от младшего к старшему

Порядок от старшего к младшему

Порядок от старшего к младшему или «тупоконечный» (англ. big-endian ): , запись начинается со старшего и заканчивается младшим. Этот порядок является стандартным для протоколов TCP/IP, он используется в заголовках пакетов данных и во многих протоколах более высокого уровня, разработанных для использования поверх TCP/IP. Поэтому, порядок байтов от старшего к младшему часто называют сетевым порядком байтов (англ. network byte order ). Этот порядок байтов используется процессорами IBM 360/370/390, Motorola 68000, порядок байтов Motorola, Motorola byte order).

В этом же виде (но с факторизацией по основанию 10) записываются числа индийско-арабскими цифрами.

Порядок байтов от старшего к младшему применяется в многих форматах файлов — например, PNG.

Переключаемый порядок

Смешанный порядок

Смешанный порядок байтов (англ. middle-endian) иногда используется при работе с числами, длина которых превышает машинное слово. Производится факторизация числа на машинные слова, которые записываются в формате, естественном для данной архитектуры, но сами слова записываются в обратном порядке.

Классический пример middle-endian — представление 4-байтных целых чисел на 16-битных процессорах семейства

В процессорах ARM используется смешанное представление для длинных вещественных чисел.

Пример

Далее приведён пример, в котором описывается размещение 4-байтового числа в ОЗУ ЭВМ, доступ к которому может производиться как к 32-разрядному слову, так и побайтно.

Все числа записаны в 16-тиричной системе счисления.

Сравнение

Существенным достоинством little-endian по сравнению с big-endian порядком записи считается возможность «неявной типизации» целых чисел при чтении меньшего объёма байт (при условии, что читаемое число помещается в диапазон). Так, если в ячейке памяти содержится число 0x00000022, то прочитав его как int16 (два байта) мы получим число 0x0022, прочитав один байт — число 0x22.

Обратно, считается что у little-endian, по сравнению с big-endian есть «неочевидность» значения байтов памяти при отладке (последовательность байтов (33, 44, 55, 12) на самом деле значит 0x12554433, для big-endian эта последовательность (33, 44, 55, 12) читалась бы «естественным» для арабской записи чисел образом: 0x33445512). Наименее удобным в работе считается middle-endian формат записи; он сохранился только на старых платформах.

Для записи длинных чисел (чисел, длина которых существенно превышает разрядность машины) обычно предпочтительнее порядок слов в числе little-endian (поскольку арифметические операции над длинными числами производятся от младших разрядов к старшим). Порядок байтов в слове — обычный для данной архитектуры.

Проблемы совместимости

Запись многобайтового числа из памяти компьютера в файл или передача по сети требует соблюдения соглашений о том, какой из байтов является старшим, а какой младшим. Прямая запись ячеек памяти приводит к возможным проблемам при переносе приложения с платформы на платформу.

Определение порядка байтов

Порядок байтов в конкретной машине можно определить с помощью программы на языке Си (testendian.c):

Результаты запуска на big-endian машине (

Результаты запуска на little-endian машине (

Конвертация

В случае совпадения текущего порядка байтов и сетевого, функции могут быть «пустыми» (то есть, не менять порядка байтов). Стандарт также допускает, чтобы эти функции были реализованы макросами.

Интересные факты

См. также

Ссылки

Полезное

Смотреть что такое «Порядок байт» в других словарях:

Сетевой порядок байт — … Википедия

порядок следования байтов — Под этим термином понимается порядок хранения байтов в машинном слове (или двойном слове). Порядок может быть «прямым» (т.е. 32 битовое число хранится так 0x12345678) и тогда говорят «big endianness» (на отечественном жаргоне… … Справочник технического переводчика

порядок передачи — информации на всех диаграммах в данной Рекомендации сначала слева направо, а затем сверху вниз. Внутри каждого байта старший значащий байт передается первым. На всех диаграммах старший значащий байт показывается слева. (МСЭ T G.7041/ Y.1303).… … Справочник технического переводчика

Порядок байтов — Порядок байтов метод записи байтов многобайтовых чисел в информатике. В общем случае, для представления числа M, большего 255 (здесь максимальное целое число, записываемое одним октетом), приходится использовать несколько байтов… … Википедия

Золотой Байт — Тип IT чемпионат Основатели Компьютерная Академия «ШАГ» Расположение … Википедия

обратный порядок байтов — Способ хранения и обмена данными в сети, при котором сначала передается самый младший байт, а затем остальные в порядке, обратном их размещению в блоке данных. [Л.М. Невдяев. Телекоммуникационные технологии. Англо русский толковый словарь… … Справочник технического переводчика

прямой порядок (следования) байтов — Формат для хранения и передачи двоичных данных, при которой старший (наиболее значимый бит (или байт) передается сначала. Обратное преобразование называется little endian. [http://www.morepc.ru/dict/] Тематики информационные технологии в целом EN … Справочник технического переводчика

Zettabyte File System — ZFS (Zettabyte File System) файловая система, изначально созданная в Sun Microsystems для операционной системы Solaris. Эта файловая система поддерживает большие объёмы данных, объединяет концепции файловой системы и менеджера логических… … Википедия

Sun ZFS — ZFS (Zettabyte File System) файловая система, изначально созданная в Sun Microsystems для операционной системы Solaris. Эта файловая система поддерживает большие объёмы данных, объединяет концепции файловой системы и менеджера логических дисков… … Википедия

Источник