что значит стационарные точки функции
Что значит стационарные точки функции
Определения:
Экстремумом называют максимальное или минимальное значение функции на заданном множестве.
Точка экстремума – это точка, в которой достигается максимальное или минимальное значение функции.
Точка максимума – это точка, в которой достигается максимальное значение функции.
Точка минимума – это точка, в которой достигается минимальное значение функции.
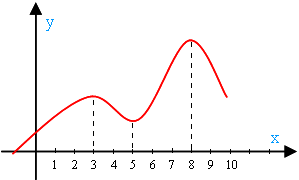
На рисунке в окрестности точки х = 3 функция достигает максимального значения (то есть в окрестности именно этой точки нет точки выше). В окрестности х = 8 она опять же имеет максимальное значение (снова уточним: именно в этой окрестности нет точки выше). В этих точках возрастание сменяется убыванием. Они являются точками максимума:
В окрестности точки х = 5 достигается минимальное значение функции (то есть в окрестности х=5 точки ниже нет). В этой точке убывание сменяется возрастанием. Она является точкой минимума:
Точки максимума и минимума являются точками экстремума функции, а значения функции в этих точках – ее экстремумами.
Точка xо является точкой максимума, если у нее существует окрестность, во всех точках которой f(x) меньше или равно f(xо):
Упрощенная формулировка : если в точке xо производная меняет знак с плюса на минус, то xо является точкой максимума.
Точка хо является точкой минимума, если у нее существует окрестность, во всех точках которой f(x) больше или равно f(xо):
Упрощенная формулировка : если в точке xо производная меняет знак с минуса на плюс, то xо является точкой минимума.
Критические и стационарные точки функции:
Внутренние точки области определения функции, в которых функция непрерывна, но производная не существует, называют критическими точками.
Внутренние точки области определения функции, при которых производная функции равна нулю, называются стационарными точками.
Необходимое условие экстремума:
Если xо – точка экстремума функции f (x), то в этой точке либо производная обращается в нуль (и это стационарная точка), либо производная не существует (критическая точка).
Достаточное условие экстремума:
Пусть xо – критическая точка. Если производная f ′(x) при переходе слева направо через точку xо меняет знак плюс на минус, то xо – точка максимума:
Если производная f ′(x) при переходе слева направо через точку xо меняет знак минус на плюс, то xо – точка минимума:
Если при переходе через критическую точку производная не меняет знак, то в точке xо экстремума нет.
На отрезке [a,b] функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b].
Алгоритм исследования непрерывной функции y = f(x) на монотонность и экстремумы:
2) Найти стационарные (f ′(x) = 0) и критические (f ′(x) не существует) точки функции y = f(x).
3) Отметить стационарные и критические точки на числовой прямой и определить знаки производной на получившихся промежутках.
4) Сделать выводы о монотонности функции и ее точках экстремума.
Стационарная точка
Смотреть что такое «Стационарная точка» в других словарях:
Стационарная точка — [stationary point] точка, в которой все частные производные первого порядка рассматриваемой функции от нескольких переменных равны нулю и тем самым градиент дифференцируемой функции обращается в нуль. Любая экстремальная точка (экстремум)… … Экономико-математический словарь
Стационарная точка — … Википедия
Седловая точка — функции z=x2 y2 (обозначена красным) … Википедия
Стандартное отображение — (англ. Standard map), известное также как стандартное отображение Чирикова (англ. Chirikov standard map) и отображение Чирикова Тейлора (англ. Chirikov Taylor map) нелинейное отображение (что сохраняет объем) для двух… … Википедия
СТАЦИОНАРНОЙ ФАЗЫ МЕТОД — метод вычисления асимптотики интегралов от быстро осциллирующих функций: где большой параметр, ограниченная область, функция S(x) (фаза) действительная, функция f(х) комплексная, и Если т. е. f финитна, и фаза S(x)не имеет стационарных точек (т.… … Математическая энциклопедия
С — Сальдо (balance) Cальдо внешней торговли [balance of trade] Сальдо государственного бюджета [balance of state budget] Сальдо торгового баланса см. Сальдо внешней … Экономико-математический словарь
РАВНОВЕСИЯ ПОЛОЖЕНИЕ — системы обыкновенных дифференциальных уравнений (*) точка такая, что х=xявляется (постоянным по времени) решением системы (*); Р. п. наз. также и само это решение. Точка есть Р. п. системы (*) тогда и только тогда, когда f(t,x) = 0 при всех t.… … Математическая энциклопедия
Троянские астероиды Нептуна — вблизи точки L4, рядом для сравнения показаны плутино … Википедия
МАКСИМУМА ПРИНЦИП — дискретный принцип максимума Понтрягина для дискретных по времени процессов управления. Для такого процесса М. п. может не выполняться, хотя для его непрерывного аналога, получающегося заменой конечно разностного оператора на дифференциальный… … Математическая энциклопедия
Действие (механика) — В физике принцип действия является утверждением о природе движения, из которого может быть определена траектория объекта, на который действуют внешние силы. Траектория объекта та, которая приводит к постоянному значению для физической величины,… … Википедия
Точки экстремума. Стационарные точки. Достаточное условие существования точки локального экстремума.
Определение
Точка 
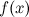


Точка 
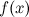

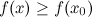
Точка 



Точка 



Наибольшее или наименьшее значение функции на промежутке называется глобальным экстремумом.
Замечание
Глобальный экстремум может достигаться либо в точках локального экстремума, либо на концах отрезка.
Необходимое условие экстремума
Теорема
(Необходимое условие экстремума)
Если функция 


Точки, в которых производная равна нулю: 
Замечание
Не в каждой своей критической точке функция обязательно имеет максимум или минимум.
Первое достаточное условие экстремума
Теорема
(Первое достаточное условие экстремума)
Пусть для функции 
1. функция непрерывна в окрестности точки 
2. 

3. производная 

Тогда в точке 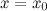



Если производная 

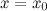
Таким образом, для того чтобы исследовать функцию 
1. найти производную 
2. найти критические точки, то есть такие значения 


3. исследовать знак производной слева и справа от каждой критической точки;
4. найти значение функции в экстремальных точках.
Второе достаточное условие экстремума
Теорема
(Второе достаточное условие экстремума)
Пусть для функции 
1. она непрерывна в окрестности точки 
2. первая производная 

3. 

Тогда в точке 

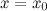

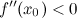
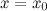

Выпуклость и точки перегиба. Основные понятия и определения. Достаточное условие выпуклости функции.
Определение. Кривая обращена выпуклостью вверх на интервале (а, b), если все ее точки лежат ниже любой ее касательной на этом интервале. Кривая, обращенная выпуклостью вверх, называется выпуклой, а кривая, обращенная выпуклостью вниз – называется вогнутой.
На рисунке показана иллюстрация приведенного выше определения.
Теорема 1. Если во всех точках интервала (a, b) вторая производная функции f(x) отрицательна, то кривая y = f(x) обращена выпуклостью вверх (выпукла).
Доказательство. Пусть х0 Î (a, b). Проведем касательную к кривой в этой точке.
Уравнение кривой: y = f(x);
Уравнение касательной:
Следует доказать, что 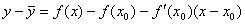
По теореме Лагранжа для f(x) – f(x0): 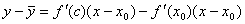

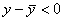
Пусть x 0 на интервале (a, b), то кривая y=f(x) вогнута на интервале (a, b).
Определение. Точка, отделяющая выпуклую часть кривой от вогнутой, называется точкой перегиба.
Очевидно, что в точке перегиба касательная пересекает кривую.
Теорема 2. Пусть кривая определяется уравнением y = f(x). Если вторая производная f¢¢(a) = 0 или f¢¢(a) не существует и при переходе через точку х = а f¢¢(x) меняет знак, то точка кривой с абсциссой х = а является точкой перегиба.
Доказательство. 1) Пусть f¢¢(x) 0 при x > a. Тогда при
x a кривая вогнута, т.е. точка х = а – точка перегиба.
2) Пусть f¢¢(x) > 0 при x b – выпуклостью вверх. Тогда x = b – точка перегиба.
Алгебра и начала математического анализа. 11 класс
Конспект урока
Алгебра и начала математического анализа, 11 класс
Урок № 16. Экстремумы функции.
Перечень вопросов, рассматриваемых в теме
1) Определение точек максимума и минимума функции
2) Определение точки экстремума функции
3) Условия достаточные для нахождения точек экстремума функции
Возрастание функции. Функция y=f(x) возрастает на интервале X, если для любых х1 и х2, 

Максимум функции. Значение функции в точке максимума называют максимумом функции
Минимум функции. Значение функции в точке минимума называют минимумом функции
Производная (функции в точке) — основное понятие дифференциального исчисления, которое характеризует скорость изменения функции (в конкретной точке).
Точка максимума функции. Точку х0 называют точкой максимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство 
Точка минимума функции. Точку х0 называют точкой минимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство 
Точки экстремума функции. Точки минимума и максимума называют точками экстремума.
Убывание функции. Функция y = f(x) убывает на интервале X, если для любых х1 и х2, 

Алгоритм исследования функции на монотонность и экстремумы:
1) Найти область определения функции D(f)
3) Найти стационарные (f'(x) = 0) и критические (f'(x) не
существует) точки функции y = f(x).
4) Отметить стационарные и критические точки на числовой
прямой и определить знаки производной на получившихся
5) Сделать выводы о монотонности функции и точках ее
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.
Теоретический материал для самостоятельного изучения
Точки, в которых происходит изменение характера монотонности функции – это ТОЧКИ ЭКСТРЕМУМА.
Точки максимума и минимума – точки экстремума.
Функция может иметь неограниченное количество экстремумов.
Критическая точка – это точка, производная в которой равна 0 или не существует.
Важно помнить, что любая точка экстремума является критической точкой, но не всякая критическая является экстремальной.
Алгоритм нахождения максимума/минимума функции на отрезке:
Примеры и разбор решения заданий тренировочного модуля
Решение: Найдем производную заданной функции: у’=2x-8
Определяем знак производной функции и изобразим на рисунке, следовательно, функция возрастает при хϵ (4;+∞); убывает при хϵ (-∞;4)
Ответ: возрастает при хϵ (4;+∞); убывает при хϵ (-∞;4)
№2. Найдите точку минимума функции у= 2х-ln(х+3)+9
Решение: Найдем производную заданной функции:
Найдем нули производной:
Определим знаки производной функции и изобразим на рисунке поведение функции:
Решение: Если нас интересует движение автомобиля, то, принимая в качестве функции зависимость пройденного расстояния от времени, с помощью производной мы получим зависимость скорости от времени.
V=х'(t)= 20t – 48. Подставляем вместо t 3c и получаем ответ. V=12 м\c
№4. На рисунке изображен график функции. На оси абсцисс отмечены семь точек: x1, x2, x3, x4, x5, x6, x7. Определите количество целых точек, в которых производная функции отрицательна.
Решение: Производная функции отрицательна на тех интервалах, на которых функция убывает. В данном случае это точки х3,х5,х7. Следовательно, таких точек 3