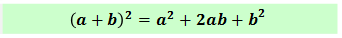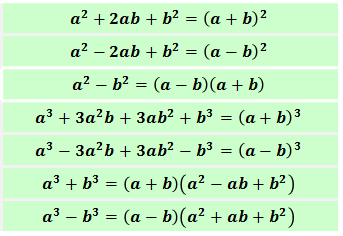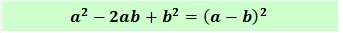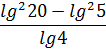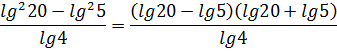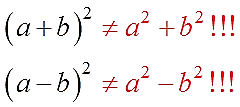что значит утроенное произведение
Формулы сокращенного умножения.
Математические выражения (формулы) сокращённого умножения (квадрат суммы и разности, куб суммы и разности, разность квадратов, сумма и разность кубов) крайне не заменимы во многих областях точных наук. Эти 7 символьных записей не заменимы при упрощении выражений, решении уравнений, при умножении многочленов, сокращении дробей, решении интегралов и многом другом. А значит будет очень полезно разобраться как они получаются, для чего они нужны, и самое главное, как их запомнить и потом применять. Потом применяя формулы сокращенного умножения на практике самым сложным будет увидеть, что есть х и что есть у. Очевидно, что никаких ограничений для a и b нет, а значит это могут быть любые числовые или буквенные выражения.
Четвертая (х + у) 3 = х 3 + 3х 2 у + 3ху 2 + у 3. Чтобы вычислить куб суммы двух выражений нужно к кубу первого выражения прибавить утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.
Шестая х 3 + у 3 = (х + у) (х 2 — ху + у 2 ) Чтобы высчитать сумму кубов двух выражений нужно умножить суммы первого и второго выражения на неполный квадрат разности этих выражений.
Не сложно запомнить, что все формулы применяются для произведения расчетов и в противоположном направлении (справа налево).
О существовании этих закономе рностей з нали еще около 4 тысяч лет тому назад. Их широко применяли жители древнего Вавилона и Египта. Но в те эпохи они выражались словесно или геометрически и при расчетах не использовали буквы.
Первым эту математическую закономерность доказал древнегреческий учёный Евклид, работавший в Александрии в III веке до н.э., он использовал для этого геометрический способ доказательства формулы, так как буквами для обозначения чисел не пользовались и учёные древней Эллады. Ими повсеместно употреблялись не “а 2 ”, а “квадрат на отрезке а”, не “ab”, а “прямоугольник, заключенный между отрезками a и b”.
И так Евклид взял квадрат со стороной (a + b):
С другой стороны, этот же квадрат он представить иначе, разделив сторону на а и b:
Тогда площадь квадрата можно представить в виде суммы площадей:
И так как квадраты были одинаковы, то их площади равны, и это значит:
Таким образом, была доказана геометрически формула квадрата суммы.
Формулы сокращенного умножения. Разложение на множители.
теория по математике 📈 алгебраические выражения
Очень часто нам встречаются выражения, которые требуют различных преобразований. Для того, чтобы это короче выполнять в некоторых случаях, существуют специальные формулы сокращенного умножения.
Квадрат суммы и квадрат разности
Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений плюс квадрат второго выражения:
(a+b) 2 =a 2 +2ab+b 2
Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений плюс квадрат второго выражения:
(a–b) 2 =a 2 –2ab+b 2
Если сравнить два этих правила и формулы, то видно, что при возведении в квадрат есть отличие в знаках только перед удвоенным произведением. Рассмотрим применение данных формул на примерах.
Куб суммы и разности
Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения и второго плюс утроенное произведение первого выражения и квадрата второго плюс куб второго выражения:
(a+b) 3 =a 3 +3a 2 b+3ab 2 +b 3
Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения и второго плюс утроенное произведение первого выражения и квадрата второго минус куб второго выражения:
(a–b) 3 =a 3 –3a 2 b+3ab 2 –b 3
Используя данные формулы, можно возводить в куб сумму и разность двух выражений. В данном случае не нужно выполнять промежуточные действия устно, чтобы избежать ошибок.
Пример №5. Возведем в куб сумму с+5а. Всё выполним и распишем строго по формуле:
Пример №6. Возведем в куб разность:
(х–10) 3 =х 3 –3х 2 10+3х10 2 –10 3 =х 3 –30х 2 +300х–1000.
Произведение разности двух выражений и их суммы равно разности квадратов этих выражений:
a 2 –b 2 =(a–b)(a+b)
Пример №7. Выполним умножение: (4–с)(4+с)=4 2 –с 2 =16–с 2 в данном выражении выполнили всё в соответствии с формулой: возвели в квадрат 4 и число с. Промежуточные записи (выделены жирным шрифтом) можно не делать, а выполнять их устно.
Пример №8. Упростим выражение: (5с+а)(5с–а)=25с 2 –а 2 в данном выражении мы видим, что первый множитель сумма, а второй – разность. Для выполнения задания по данной формуле это не имеет значения, так как мы знаем, что от перестановки множителей произведение не изменяется.
Применение формул сокращенного умножения для разложения многочленов на множители
Рассмотрим тождество, которое называют разностью квадратов двух выражений:
a 2 –b 2 =(a–b)(a+b)
Разность квадратов двух выражений равна произведению разности этих выражений и их суммы. Эту формулу применяют для разложения на множители многочлена, содержащего разность квадратов. Рассмотрим на примерах.
Пример №10. Разложить на множители: х 2 у 2 –81=(ху–9)(ху+9). В данном выражении выполнено всё в соответствии с формулой, промежуточные записи не использованы.
Пример №11. Представим в виде произведения: х 4 –36=(х 2 –6)(х 2 +6). В данном выражении мы видим, что степень переменной может быть не только вторая, но и любая четная, чтобы ее можно было представить в виде квадрата переменной.
Пример №12. Представим в виде произведения х 10 с 6 –25=(х 5 с 3 –5)(х 5 с 3 +5). Здесь показаны разные четные степени переменных.
Для разложения на множители суммы и разности кубов существуют определенные правила и формулы.
Сумма и разность кубов
Сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности:
a 3 +b 3 =(a+b)(a 2 –ab+b 2 )
Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы:
a 3 –b 3 =(a–b)(a 2 +ab+b 2 )
Разложение многочлена формулой квадрата суммы и разности
Формулы квадрата суммы и квадрата разности также используют для разложения многочлена на множители. Для этого формулы записываются в обратном порядке, то есть меняются левая и правая части местами:
a 2 +2ab+b 2 =(a+b) 2
a 2 –2ab+b 2 =(a–b) 2
P.S. Все формулы на одной картинке:
В данном случае необходимо сначала упростить выражение, для этого раскроем скобки:
(x + 5) 2 — x (x — 10) = x 2 + 2 • 5 • x + 25 — x 2 + 10x
Затем приведем подобные слагаемые:
x 2 + 2 • 5 • x + 25 — x 2 + 10x = 20 x + 25
Далее подставим x из условия:
20 x + 25 = 20 • (-1/20) + 25 = — 1 + 25 = 24
pазбирался: Даниил Романович | обсудить разбор | оценить
Формулы сокращённого умножения
Формулы сокращённого умножения необходимы во всех разделах математики. От элементарной до высшей. Они применяются практически везде — в упрощении выражений, решении уравнений и неравенств, сокращении дробей, вычислении пределов, решении интегралов — список можно продолжать ещё долго…
Следовательно, нужно основательно разобраться с этими формулами. Понять, откуда они берутся, зачем они нужны, как их применять на практике и, самое главное, как их запомнить. А запомнить всё-таки придётся, да…
Квадрат суммы, квадрат разности, разность квадратов, куб суммы, куб разности, сумма кубов, разность кубов — что за звери?
Итак, вот они, формулы сокращённого умножения:
Эти семь формул — полный джентльменский набор. Последние две формулы (сумма и разность кубов) записаны не так как в большинстве учебников, а наоборот — справа налево. Это не просто так.) Любая формула в математике работает в обоих направлениях — как туда, так и обратно. Именно такая запись наиболее наглядно показывает, откуда берутся формулы сокращённого умножения.
Они берутся из… умножения. Вот ведь удивил, да?) Что ж, смотрите сами. Берём, например, самую первую формулу по списку:
Вот и все дела. Самое обычное перемножение скобок и приведение подобных. Именно так и получаются все формулы сокращённого умножения. Сокращённое умножение — потому, что в самих формулах нет раскрытия скобок и приведения подобных. Эти промежуточные действия сокращены. Сразу дан готовый результат. Пользуйтесь на здоровье!
Эти формулы надо знать наизусть. Без знания первых трёх формул, с квадратами, даже не мечтайте о тройке! Без всех остальных (с кубами) — о четвёрке и выше. Нет-нет, бросаться зубрить весь этот список прямо сейчас мы не будем.) Об этом позже. Пока просто знакомимся.)
Зачем нужны формулы сокращённого умножения?
Полезная вещь первая — самая очевидная. Это быстрое (т.е. сокращённое) умножение многих алгебраических выражений без промежуточных выкладок. Меньше выкладок — меньше и ошибок. Но это не самая главная полезная вещь! А вот вторая.
Сравним два равенства:
Для математики эти два равенства абсолютно одинаковы. А вот для нас с вами — не совсем. Возьмём первую запись, слева направо:
Это самое обычное умножение скобок, не более того. Никаких принципиально новых возможностей. А теперь возьмём второй вариант того же равенства, справа налево:
А вот такая запись резко повышает уровень вашей математической культуры! Почему? Потому, что такая запись формулы, справа налево, — это разложение на множители! А разложение на множители — процедура поважнее простого умножения, да…) Сомневаетесь? Не надо. В соответствующей теме подробно расскажу.)
И такое разложение на множители имеет место быть во всех формулах сокращённого умножения! Почему? Давайте внимательно посмотрим на наш список. В левой части каждой формулы мы увидим перемножение скобок:
Стало быть, левая часть каждой формулы разложена на множители, а вот правая часть — нет. Список, что приведён выше, — это, действительно, всего лишь сокращённое умножение. Но! Стоит только поменять местами левую и правую части каждой из формул, как тот же самый список становится формулами разложения на множители!
Для полного понимания перепишу этот список ещё разок, но справа налево. Вот так:
Такая обратная запись формул сокращённого умножения идеально подходит для разложения на множители многочленов, для сокращения алгебраических дробей и для решения самых разнообразных примеров. Но есть существенная проблема. Как их запомнить?
Запоминаем формулы сокращённого умножения! Секретные приёмы…
С выражениями (a+b) 3 и (a—b) 3 всё то же самое — куб суммы и куб разности соответственно.
Надеюсь, что названия сумма кубов и разность кубов у вас уже не вызовут недоумения?
А вот теперь начинается самое сложное — запоминание самих формул, со всеми этими выражениями. К сожалению, здесь тот самый случай, когда без механической памяти не обойтись. Это огорчает.
Однако здесь у нас с вами тайные знания! Эти знания помогут вам побыстрее сориентироваться во всех этих скобках, плюсах/минусах, квадратах/кубах, сведя механическую зубрёжку к минимуму. Читаем дальше и вникаем.
Итак, начинаем с квадрата суммы:
Просто медитировать, сверля формулу взглядом, будет недостаточно. Для лучшего запоминания настоятельно рекомендую выучить (да-да, именно выучить!) словесную формулировку:
Квадрат суммы двух выражений равен квадрату первого выражения ПЛЮС удвоенное произведение первого выражения на второе ПЛЮС квадрат второго выражения.
Эта мантра реально облегчает жизнь во многих разделах школьной математики! Да и в институте, при работе со всякими там пределами да интегралами, тоже. Ещё не раз вспомните эту формулировку добрым словом!)
Если вы запомнили квадрат суммы, то дальше будет проще. Можно включать логику и здравый смысл. Переходим к квадрату разности:
Сравните с квадратом суммы! Нашли отличие? Да! Перед удвоенным произведением появился минус. Ведь должен же он где-то появиться?! Перед a 2 и b 2 он появиться никак не может, ибо любое число в квадрате есть число положительное. Остаётся только серединка.) Для понимания рекомендую просто перемножить скобки сами на себя да привести подобные. И тогда у вас пропадут все вопросы.
В словесной расшифровке:
Квадрат разности двух выражений равен квадрату первого выражения МИНУС удвоенное произведение первого выражения на второе ПЛЮС квадрат второго выражения.
Эта формула обычно и так легко запоминается. Единственное, можно случайно влепить в скобки два плюса или два минуса. Но тогда это уже будут квадрат суммы и квадрат разности. А это — совсем другие формулы…
Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.
Переходим к следующей группе формул — к сумме и разности кубов:
Приём для запоминания здесь следующий. В первых скобках (маленьких) знак совпадает со знаком в исходном выражении: плюс-плюс, минус-минус. А вот во вторых (больших) скобках — меняется на противоположный. Причём меняется не перед квадратами, а снова посерединке! Квадраты a 2 и b 2 — положительные!
Кстати, посмотрите внимательнее на большие скобки в каждой из формул и сравните с формулами квадрата суммы и квадрата разности!
Нашли отличия? Да! В кубах не хватает двойки посерёдке. Именно по этой причине выражения в больших скобках
часто называют неполным квадратом суммы/разности.
А теперь можно и шаблонные словесные формулировки из учебников привести:
Сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.
Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.
Остаётся последняя парочка — куб суммы и куб разности:
Эти две формулы встречаются в заданиях пореже предыдущих пяти, но знать их тоже не помешает, да. Претендуете на пятёрку? Тогда читаем дальше!
Итак, как запомнить куб суммы? Во-первых, все знаки в формуле — плюсы! Оно и естественно. Ведь мы же перемножаем только положительные выражения, так с какого перепугу минусам-то взяться? Первое и последнее слагаемые — чистые кубы первого и второго выражений. А вот по центру — утроенные произведения.
Но и это ещё не всё! Смотрите-ка, какая интересная штука: сумма степеней a и b в каждом из слагаемых всегда равна трём! Например:
Такой порядок хорошо помогает не запутаться.)
Если вы уловили принцип запоминания куба суммы, то куб разности запомнится без проблем. Всё то же самое, только минусы надо правильно расставить. А это очень легко сообразить! Какая переменная у нас с минусом? Правильно, переменная b! Следовательно, в слагаемых, где b стоит в первой степени и в кубе — будет минус. Ибо любой минус в нечётной степени всегда даёт минус. А вот минус в квадрате (b 2 ) даст плюс. И все дела.)
Разумеется, изложенные выше советы — это не жёсткие правила математики. Это просто практические приёмы, помогающие более быстрому и комфортному запоминанию. Чисто для себя. Куда уж лучше, чем механическая зубрёжка, правда?)
Но, как ни крути, самый надёжный способ запомнить эти формулы — решать побольше примеров. Тогда весь этот перечень запомнится очень быстро. Сам собой, можно сказать.
Ну что, потренируемся?)
Примеры на формулы сокращённого умножения.
Начнём с самого простого — с прямого применения формул. Для разминки.)
Преобразовать в многочлен:
Сразу видим квадрат скобок. А в скобках — сумму. Значит, работаем по самой первой формуле, вот этой:
Идём дальше: «Плюс удвоенное произведение первого выражения на второе…». Удвоенное — это умножение на двойку. Первое выражение — это 5x, второе — это 4y. Продолжаем:
Практически всё. Осталось «причесать» удвоенное произведение (перемножить 2∙5∙4) и получим окончательный ответ:
Это было разминочное задание. А теперь примерчик посерьёзнее.
Разложить на множители:
Что, внушает? Опять смотрим на наш список. Но не на тот, что в начале урока (для умножения), а на второй, для разложения на множители. Вот на этот:
Тут, разумеется, нашего выражения нет. Ну и что? Здесь важно понимать, что под буквами a и b может скрываться всё что угодно — и числа, и другие буквы, и более сложные выражения. Поэтому смотрим на список и ищем похожую формулу. И зацепкой будут степени переменной.
В нашем выражении есть x 2 и просто x. Ясное дело, отбрасываем все формулы с кубами — у нас их явно нет. Далее выкидываем из рассмотрения формулу разности квадратов: там нет переменных в первой степени, только квадраты. А у нас — есть.
Остаются первые две формулы — квадрат суммы или квадрат разности. Уже проще, не так ли? Осталось сообразить, что в формуле квадрата суммы — только плюсы. А в нашем выражении в серединке стоит минус. Стало быть, похожая формула — это квадрат разности.
Но не факт, что квадрат разности сработает, совсем не факт… Наша задача — убедиться, что предложенное выражение 4x 2 –20x+25 точно соответствует квадрату разности. Только тогда у нас появится возможность записать и правую часть равенства (т.е. разложение на множители).
Для удобства я перепишу формулу и исходное выражение прямо одно под другим:
Всё? Можно записывать разложение? Пока нет.
Нужна последняя, контрольная проверка по выражению 20х. Надо убедиться, что наши 20х точно соответствуют удвоенному произведению 2ab.
Итак, затаив дыхание составляем удвоенное произведение первого и второго выражений:
Ура! Совпало! Значит, наше выражение — это действительно квадрат разности 2х и 5. Вот теперь можно со спокойной душой записывать ответ:
Идея ясна? Сначала ищем в списке похожую формулу, а затем сверяем с ней выражение, предложенное в задании, на полное соответствие. Если повезло и всё совпало, то записываем ответ. Если не повезло, то, значит, раскладывать надо как-то иначе.
Это были самые простые примеры, для младшеньких. А теперь переместимся в старшие классы, с их синусами да логарифмами. Да-да, старшеньким формулы сокращённого умножения тоже бывают нужны!
Например, такое задание:
Вся мощь тригонометрии слабо помогает в этом примере. Только алгебра седьмого класса и спасает, да…
Конечно, это выражение сильно смахивает на квадрат разности. Вот и пробуем применить эту формулу к нашему выражению! Что будет скрываться под буквами a и b? Конечно же, cos 2 x и sin 2 x. Удвоенное произведение, ясен перец, будет 2cos 2 x∙sin 2 x, как, собственно, в нашем выражении и записано. Смело сворачиваем нашего монстра в квадрат разности по формуле:
А вот теперь и тригонометрия в игру вступает! Что у нас в скобочках? У нас в скобочках косинус двойного угла!
Пример не подарок, прямо скажем… Логарифмические формулы явно не катят, да и сами логарифмы ровно не считаются… Проверим на алгебру? Числитель явно намекает на применение формулы разности квадратов.
В роли a и b у нас логарифмы. Ну и что? Это формулу никак не портит, ибо законы алгебры работают во всей математике. Смело заменяем числитель дроби на произведение скобок и пишем:
А вот теперь и логарифмические формулы заработали! В первых скобках (разность) получается lg4, который и сокращается благополучно со знаменателем. А во вторых скобках (сумма) будет lg100. Что по свойствам логарифмов есть 2.
Конечно, подобные примеры в этом уроке легко решаются. Но на практике, когда ученик глубоко погружён в синусы/косинусы да логарифмы, разложение на множители просто не приходит в голову…
Посему практический совет:
Проверяем замороченные примеры на алгебру седьмого класса! В частности, на формулы сокращённого умножения.
О типичном ляпе, который сразу же показывает блистательное отсутствие хоть какого-то понимания. Ляп настолько часто встречается, что хочется заявить громко:
И запомните это крепко-накрепко!
Формулы — штука жёсткая! Раз требуют удвоенного произведения 2ab, помимо чистых квадратов, значит спорить бессмысленно. Напишете такое на контрольной — будьте готовы получить заслуженную двойку! Такого не прощают. Вот так.
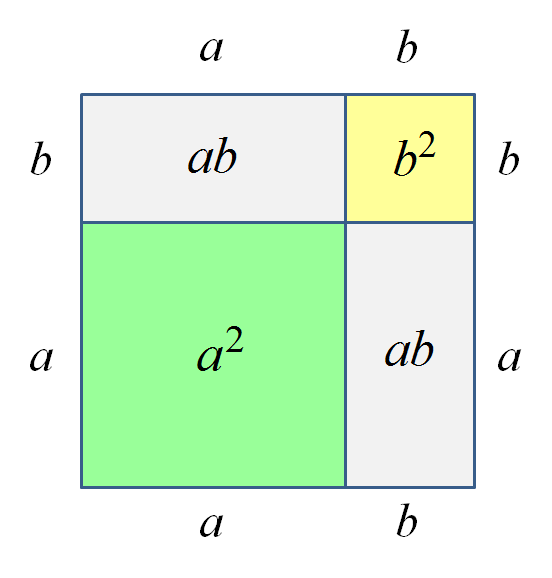
Наглядный пример на добрую память с квадратом суммы. Всё-таки картинки иногда проливают свет на очень многие волнующие вопросы. Нарисуем в тетрадке квадрат со стороной a+b. Можно по клеточкам. Допустим, для конкретики, a — это 4 клетки, a b — это 2 клетки.
Упражнение для интересующихся: аналогичным образом доказать геометрически (т.е. через квадраты и прямоугольники) две другие формулы сокращённого умножения с квадратами — квадрат разности и разность квадратов. Попробуйте! Интересно.)
1. Преобразовать в многочлен стандартного вида: