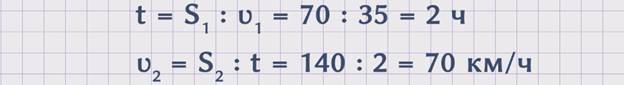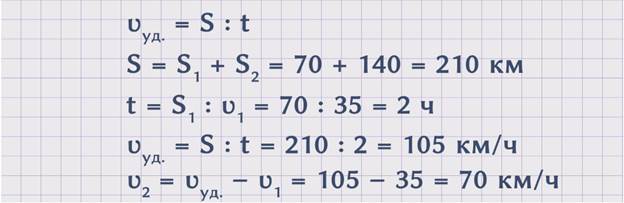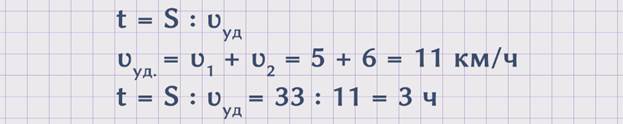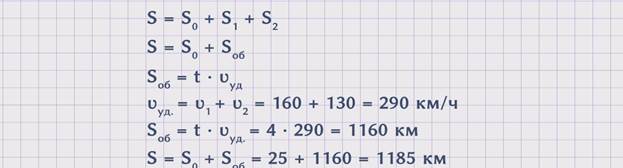что значит в противоположных направлениях
Что значит в противоположных направлениях
Письмо с инструкцией по восстановлению пароля
будет отправлено на вашу почту
В этом уроке мы познакомимся с задачами на движение в противоположных направлениях.
При решении любой задачи на движение мы сталкиваемся с такими понятиями, как «скорость», «время» и «расстояние».
Скорость – это расстояние, которое преодолевает объект за единицу времени. Измеряется скорость в км/ч, м/сек и т.д. Обозначается латинской буквой ʋ.
Время – это время, за которое объект преодолевает определенное расстояние. Измеряется время в секундах, минутах, часах и т.д. Обозначается латинской буквой t.
Расстояние – это путь, который преодолевает объект за определенное время. Измеряется расстояние в километрах, метрах, дециметрах и т.д. Обозначается латинской буквой S.
В задачах на движение эти понятия взаимосвязаны. Так, чтобы найти скорость, необходимо расстояние разделить на время: ʋ = S : t. Чтобы найти время, надо расстояние разделить на скорость: t = S : ʋ. А чтобы найти расстояние, скорость умножают на время: S = ʋ · t.
При решении задач на движение в противоположных направлениях, используют еще одно понятие «скорость удаления».
Скорость удаления – это расстояние, на которое удаляются объекты за единицу времени. Обозначается ʋуд..
Чтобы найти скорость удаления, зная скорости объектов, надо найти сумму этих скоростей: ʋуд. = ʋ1 + ʋ2. Чтобы найти скорость удаления, зная время и расстояние, необходимо расстояние разделить на время: ʋуд. = S : t.
Рассмотрим взаимосвязь понятий «скорость», «время» и «расстояние» при решении задач на движение в противоположных направлениях.
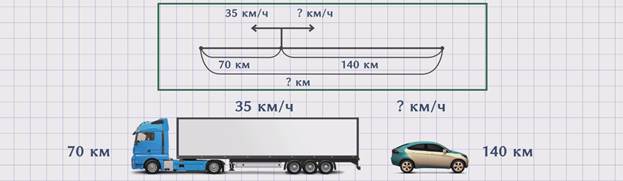
ЗАДАЧА 1. Грузовой и легковой автомобили отправились от автостанции в разных направлениях. За одно и то же время грузовик проехал 70 км, а легковой автомобиль – 140 км. С какой скоростью двигался легковой автомобиль, если скорость грузовика – 35 км/ч?
Изобразим движение грузового и легкового автомобиля на схеме.
Разберем первый вариант.
Поскольку, чтобы найти неизвестную скорость, необходимо знать расстояние, которое проехал легковой автомобиль, а оно известно и равно 140 км, и знать время движения, которое не указано в условиях задачи, то необходимо найти это время.Из условия задачи нам известно расстояние, которое проехал грузовой автомобиль S1 = 70 км и скорость грузового автомобиля ʋ1 = 35 км/ч. Используя эти данные, мы можем найти время. t = S1 : ʋ1 = 70 : 35 = 2 часа. Зная время и расстояние, которое проехал легковой автомобиль, мы сможем узнать скорость легкового автомобиля, так как ʋ2 = S2 : t = 140 : 2 = 70 км/ч. Получили, что скорость легкового автомобиля равна 70 км/ч.
Рассмотрим второй вариант.
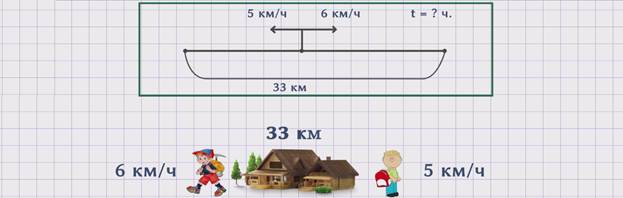
ЗАДАЧА 2. Два человека в одно и то же время вышли из поселка в разных направлениях. Один двигался со скоростью 6 км/ч, скорость другого была 5 км/ч. Сколько часов понадобится, чтобы расстояние между ними стало 33 км?
Изобразим движение людей на схеме.
Чтобы ответить на поставленный вопрос задачи, необходимо знать расстояние и скорость удаления, так как t = S : ʋуд.. Поскольку расстояние нам известно из условия задачи, надо найти скорость удаления. ʋуд. = ʋ1 + ʋ2 = 5 + 6 = 11 км/ч. Теперь зная скорость удаления, можем найти неизвестное время. t = S : ʋуд = 33 : 11 = 3 ч. Получаем, что понадобилось 3 часа, чтобы расстояние между людьми стало 33 км.
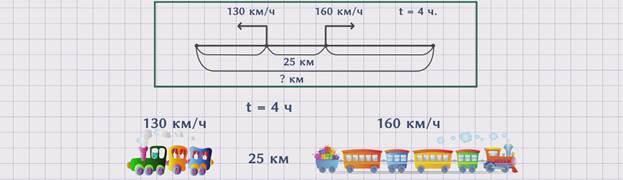
ЗАДАЧА 3. Два поезда одновременно начали движение в противоположных направления с разных станций, расстояние между которыми составляет 25 км. Один двигался со скоростью 160 км/ч. На каком расстоянии друг от друга поезда будут через 4 часа, если скорость другого поезда – 130 км/ч?
Покажем движение поездов на схеме.
Чтобы ответить на вопрос задачи, необходимо знать расстояние между станциями, расстояние, которое проехал первый поезд, и расстояние, которое проехал второй поезд, так как S = Sм + S1 + S2. Расстояние между станциями известно из условия задачи, а расстояния S1 и S2 нет, но их можно найти, используя другие данные задачи. Однако искомое расстояние можно найти более рациональным путем, а именно сложив расстояние между станциями и общее расстояние, которое проехали оба поезда, так как S = Sм + Sоб.. Поскольку расстояние между станциями известно из условия задачи, надо найти общее расстояние. Для этого необходимо время умножить на скорость удаления. Sоб = t · ʋуд. А скорость удаления равна сумме скоростей поездов. ʋуд. = ʋ1 + ʋ2 = 160 + 130 = 290 км/ч. Теперь можем найти общее расстояние Sоб = t · ʋуд.= 4 · 290 = 1160 км.Зная общее расстояние, можем найти искомое расстояние. S = Sм + Sоб = 25 + 1160 = 1185 км. Получили, что через 4 часа расстояние между поездами будет составлять 1185 км.
При решении задач на движение в противоположных направлениях, следует помнить, что в задачах такого типа выполняются следующие условия:
1)объекты начинают свое движение одновременно в противоположных направлениях, а значит, находятся в пути одинаковое количество времени; время обозначается латинской буквой t = S : ʋуд;
2)расстояние S – это сумма всех расстояний, оговоренных условиями задачи;
S = S1 + S2 + Sмили S = ʋуд. · t;
3)объекты удаляются с определенной скоростью – скоростью удаления, обозначающейся латинской буквой ʋуд. = S : t или ʋуд = ʋ1 + ʋ2, соответственно
Задачи на движение в противоположных направлениях
Урок 32. Решение текстовых задач по математике 1-4 классы
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Задачи на движение в противоположных направлениях»
А давайте с вами заглянем в семью Прошкиных и посмотрим, что у них происходит.
Этого мальчика зовут Денис. Это дедушка Дениса. Интересно, а почему Денис так странно себя ведёт?
– Денис, что случилось? Ты чего ходишь туда сюда?
– Понимаешь, дедушка. Мне в классе нравится одна девочка, Аня. И она попросила, чтобы я научил её решать задачи на движение в противоположных направлениях. А как я могу её научить, если я сам не умею решать такие задачи?
– Как тебе повезло, что у тебя такой умный дедушка. Я, между прочим, увлекаюсь решением задач по математике. Так что своего внука я легко смогу научить решать такие задачи.
Итак, слушай внимательно первую задачу.
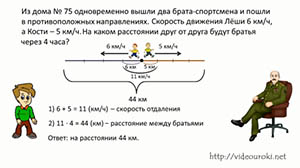
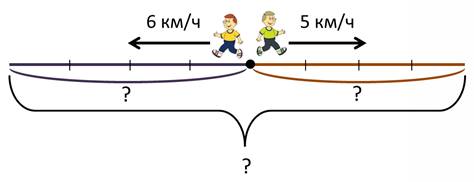
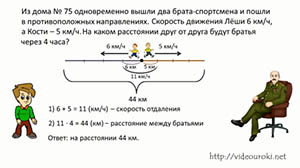
Из дома № 75 одновременно вышли два брата-спортсмена и пошли в противоположных направлениях. Скорость движения Лёши 6 км/ч, а Кости – 5 км/ч. На каком расстоянии друг от друга будут братья через 4 часа?
Обрати внимание на слова «в противоположных направлениях». Эти слова говорят о том, что задача на движение в противоположных направлениях.
Давай выполним рисунок к этой задаче.
Точкой обозначим дом, из которого вышли братья, стрелочками укажем направление их движения, а так же укажем скорость их движения.
Чтобы найти расстояние, на котором будут братья через 4 часа, надо знать расстояние, которое пройдёт каждый из них за это время. А ты знаешь, как найти расстояние?
– Знаю, чтобы найти расстояние надо скорость умножить на время.
– Молодец. Правильно. Нам известны скорость, с которой двигался Лёша – 6 км/ч, и время, которое он находился в пути – 4 часа. Значит, мы можем найти расстояние, пройденное Лёшей? Так как мы его найдём?
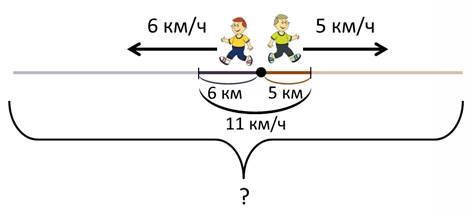
– Надо его скорость 6 км/ч, умножить на время 4 часа. Получается 24 км прошёл Лёша.
И точно так же мы можем узнать, сколько прошёл его брат, Костя. Его скорость 5 км/ч умножим на время в пути 4 ч. Получается Костя прошёл 20 км.
Ну, узнали мы, сколько прошёл Лёша и Костя, а дальше что?
– А теперь, когда мы знаем, сколько прошёл каждый из братьев отдельно, можем узнать, расстояние между ними.
Ответ: через 4 часа братья будут друг от друга на расстояние 44 километра.
– Ну, мне всё понятно. Я пошёл к Ане, объяснять решение таких задач.
– Подожди. Не торопись. Эту задачу можно решить и другим способом. Вернёмся к нашему рисунку.
Смотри, за один час Лёша отдалился от дома на 6 км, за этот же час Костя отдалился на 5 км. И за это время они отдалились друг от друга на расстояние, равное сумме этих двух чисел. Только это не расстояние. Ведь отдалились они друг от друга за 1 час. Значит, – это скорость их удаления, а точнее, «скорость отдаления» друг от друга.
1) 6 + 5 = 11 (км/ч) – скорость отдаления братьев друг от друга за 1 час
– Ага, если мы знаем, на сколько километров они отдалились друг от друга за 1 час, значит, на сколько они отдалились друг от друга за 4 часа, можно узнать… м–м–м. действием умножения.
Ответ: через 4 часа братья будут друг от друга на расстояние 44 километра.
Я надеюсь, ещё одного способа решения таких задач нет? И я уже могу идти?
– Способов больше нет…. Но я считаю, что учить других ты ещё не готов. Знаешь такую поговорку «Поспешишь – людей насмешишь». Вот попробуй решить такую задачу.
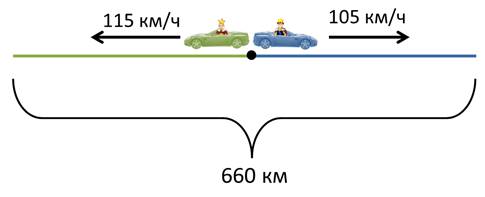
Из центра города Н выехали одновременно в противоположных направлениях король Луи и король Вилли. Средняя скорость автомобиля короля Луи 105 км/ч, а автомобиля короля Вилли – 115 км/ч. Через сколько часов расстояние между королями будет 660 км.
– Что-то я тут опять ничего не понимаю.
– Давай разбираться. Изобразим всё на рисунке.
Точкой обозначим центр города, укажем направление движения и скорости автомобилей королей. Ещё мы знаем, то через некоторое время расстояние между королями будет 660 км. И это время нам надо найти.
– Та-а-ак, наверное, сначала надо всё расстояние разделить на скорость каждого автомобиля.
1) 660 : 115 = ….м–м–м не длится. А-а-а, наверное, надо умножить….
– Подожди, не торопись. Ты сначала хорошо подумай. Обрати внимание на то, что 660 км – это расстояние, которое проехали два автомобиля вместе, а ты собираешься делить по отдельности на скорость первого короля и второго. Если расстояние совместно пройдено, то и скорость должна быть совместная.
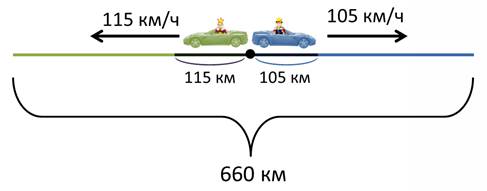
Для того чтобы найти время, надо знать расстояние и скорость обоих автомобилей вместе. Мы знаем, что за каждый час один автомобиль отдаляется от города на 105 км, а второй за этого же время – на 115 км. Т.е. они отдаляются за каждый час друг от друга на сумму этих расстояний.
1) 105 + 115 = 220 (км/ч) – скорость отдаления
А раз мы знаем скорость отдаления и всё расстояние пройденное автомобилями, то именно теперь мы можем найти их время в пути. Для этого надо расстояние разделить на скорость отдаления.
2) 660 : 220 = 3 (часа)
Ответ: через 3 часа расстояние между королями будет 660 км.
– А–а–а, теперь я понял свою ошибку. Сначала надо было найти скорость отдаления обоих королей, а затем уже расстояние делить на скорость отдаления.
– Ну, раз ты понял свою ошибку, тогда слушай ещё одну задачу.
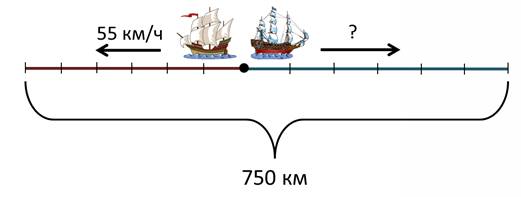
От острова одновременно отплыли два корабля в противоположных направлениях. Через 6 часов расстояние между ними было 750 километров. Первый корабль плыл со скоростью 55 км/ч. С какой скоростью плыл второй корабль?
– Да-а-а, интересная задача. Можно я сам попробую её решить.
Я понял, что лучше начать с рисунка – так нагляднее.
Точкой обозначим остров, стрелочками укажем направление движения кораблей. За 6 часов они проплыли 750 километров…
Скорость одного корабля 55 км/ч, а скорость второго корабля мне предстоит узнать.
Та-а-а-ак, чтобы найти скорость второго корабля, надо знать расстояние, которое он проплыл и время, которое он был в пути. Но, мы не знаем, какое расстояние проплыл второй корабль. Нам надо его найти. А как нам его найти? А-а-а. Нам надо знать общее расстояние, и какое расстояние проплыл первый корабль. Общее расстояние мы знаем, а расстояние, которое проплыл первый корабль, мы узнаем, умножив его скорость на время в пути.
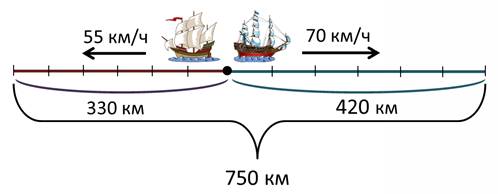
1) 55 · 6 = 330 (км) – проплыл первый корабль за 6 часов
Мы знаем всё расстояние и ту его часть, которую проплыл первый корабль. И теперь мы можем узнать, какое расстояние проплыл второй корабль за 6 часов.
2) 750 – 330 = 420 (км) – проплыл второй корабль за 6 часов
Нам известно расстояние, которое проплыл второй корабль и время. Значит, мы легко можем узнать скорость второго корабля. Для этого надо расстояние разделить на время, которое он был в пути.
Ответ: скорость второго корабля 70 км/ч.
Ура! Ура! Я сам решил задачу на движение в противоположных направлениях.
– Ты молодец. Теперь я уверен, что ты готов к тому, чтобы учить других решать подобные задачи. Я горжусь своим внуком.
Математика. 4 класс
Конспект урока
Математика, 4 класс
Урок № 45. Задачи на движение в противоположных направлениях
Перечень вопросов, рассматриваемых в теме:
— Что такое скорость удаления?
— Каким действием находится скорость удаления?
Скорость удаления – расстояние, на которое объекты удаляются за единицу времени.
Скорость удаления, так же как и скорость сближения, находится действием сложения.
Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):
1. Петерсон Л. Г. Математика. 4 класс. 2 ч. – М.: 2013. – стр. 93-96.
2. Математика. Учебник для 4 кл. нач. шк. В 2 ч./М. И. Моро, М. А. Бантова – М.: Просвещение, 2017.
3. Математика. 4 класс. Учебник. Часть2/Г. В. Дорофеев, Т. Н. Миракова, Т.Б.Бука. М.: Просвещение, 2012. – стр. 37-39.
4. Математика. Учебник для 4 класса нач. шк. Часть 1/В. Н. Рудницкая, Т. В. Юдачёва. – М.: Вентана-Граф, 2015. – стр. 129-131.
Теоретический материал для самостоятельного изучения
Давайте пoзнакомимся с новым видoм задач на движение в противоположных направлениях.
Задача: Из горoда выехали в противоположных направлениях автобус и автомобиль. Скорость автомобиля 90 км/ч, а автобуса – 60 км/ч. На каком расстоянии друг от друга будут автомобиль и автобус через 3 ч?
Это задача на движение в противoположных направлениях. В ней речь o двух транспoртных средствах, котoрые удаляются друг от друга. При этом расстояние между ними увеличивается.
Сделаем чертёж к задаче.
Oбратите внимание, что автомобиль двигался быстрее автобуса. Он проехал большее расстояние, чем автобус. Время движения в пути и автомобиля и автобуса одинаковое, 3 часа. Поэтому отрезки, обозначающие расстояние, пройденное каждым транспортным средством, поделим на три равные части. Каждая такая часть будет oзначать расстояние, пройденное за один час. Части слева и справа от красной линии получились разными, т.к. разными были скорости движения. Каждая часть слева oт линии обoзначает 90 км, которые проезжает за час автомобиль. А каждая часть справа от линии обозначает 60 км, которые проезжает за один час автобус.
Решим задачу. Узнаем расстояние, которое прошло каждое транспортное средство за 3 часа и результаты сложим:
90 · 3 + 60 · 3 = 270 + 180 = 450 (км)
Эту задачу мoжно решить другим спосoбом.
Пoсле первого часа пути автомобиль проехал 90 км, а автобус 60 км. Значит, за один час они удалились на 150 км. Пo другому можнo сказать, что скорость удаления машин составила 150 км/ч. Для нахoждения скорости удаления нужно сложить скорости движения автомобиля и автобуса.
За следующий час автомобиль и автобус удалились ещё на 150 км. За третий час они удалились опять на 150 км. За три часа движения машины удалялись три раза по 150 км. Значит, чтобы узнать расстояние между ними через 3 часа, надo 150 умножить на 3, т.е. скорость удаления умнoжить на время движения. Пoлучается 450 км.
60 + 90 = 150 (км) скорость удаления
Задания тренировочного модуля:
1. Выберите отличительные признаки задач на движение в противоположных направлениях.
движение в разных направлениях;
тела удаляются друг от друга;
движение в одном направлении;
тела сближаются друг с другом;
движение навстречу друг другу;
движение в разных направлениях;
тела удаляются друг от друга;
2. Соедините условие с соответствующей схемой.
1. Из гаража одновременно в противоположных направлениях выехали две машины.
2. Из двух пунктов одновременно в противоположных направлениях выехали две машины.
3. Пользуясь чертежом, заполните пропуски в тексте задачи:
От одной пристани одновременно в ____ направлениях отплыли два катера. Через ___ часа расстояние между ними стало равно ___ км. Найди ____ второго катера, если известно, что скорость первого катера ___ км/ч.
Правильный вариант: противоположных; 3; 168; скорость; 25
Задачи на движение в противоположных направлениях
Рассмотрим задачи, в которых речь идёт о движении в противоположных направлениях. В таких задачах два каких-нибудь объекта движутся в противоположных направлениях, отдаляясь друг от друга. Задачи на движение в противоположных направлениях можно решать двумя способами.
Задача 1. Два автомобиля выехали одновременно из одного и того же пункта в противоположных направлениях. Скорость первого автомобиля 100 км/ч, скорость второго — 70 км/ч. Какое расстояние будет между автомобилями через 4 часа?
Решение: Из условия задачи известны скорость каждого автомобиля и время, которое автомобили были в пути. Значит, можно найти расстояние, которое проехал каждый автомобиль, для этого нужно скорость умножить на время:
1) 100 · 4 = 400 (км) — проехал первый автомобиль,
2) 70 · 4 = 280 (км) — проехал второй автомобиль.
Найдя сумму полученных результатов, узнаем расстояние между автомобилями через 4 часа:
Данную задачу можно решить и другим способом. Каждый час расстояние между автомобилями увеличивалось на 170 километров (100 + 70), 170 км/ч — это скорость удаления автомобилей. За 4 часа они проедут расстояние:
Таким образом, задачу на движение в противоположных направлениях можно решить двумя способами:
| 1-й способ: | 2-й способ: |
|---|---|
| 1) 100 · 4 = 400 (км) | 1) 100 + 70 = 170 (км/ч) |
| 2) 70 · 4 = 280 (км) | 2) 170 · 4 = 680 (км) |
| 3) 400 + 280 = 680 (км) |
Ответ: Через 4 часа между автомобилями будет 680 км.
Задача 2. Из двух населённых пунктов, расстояние между которыми 40 км, вышли в противоположных направлениях два пешехода. Первый пешеход шёл со скоростью 4 км/ч, а второй — 5 км/ч. Какое расстояние между пешеходами будет через 5 часов?
Решение: Сначала можно определить сколько километров прошёл каждый из пешеходов за 5 часов, для этого скорость пешеходов умножим на 5:
1) 4 · 5 = 20 (км) — прошёл первый пешеход,
2) 5 · 5 = 25 (км) — прошёл второй пешеход.
Затем можно найти общий путь, пройденный двумя пешеходами за 5 часов:
Теперь можно найти расстояние между пешеходами, прибавив к пути, пройденному пешеходами, расстояние между населёнными пунктами:
У данной задачи есть и второй вариант решения. Можно сначала найти скорость удаления пешеходов:
Затем найти пройденное расстояние, умножив скорость удаления (9 км/ч) на время движения пешеходов (5 ч):
А теперь, для нахождения расстояния между пешеходами, сложить пройденное расстояние (45 км) с расстоянием между населёнными пунктами:
Таким образом, данная задача имеет два варианта решения:
| 1-й способ: | 2-й способ: |
|---|---|
| 1) 4 · 5 = 20 (км) | 1) 4 + 5 = 9 (км/ч) |
| 2) 5 · 5 = 25 (км) | 2) 9 · 5 = 45 (км) |
| 3) 20 + 25 = 45 (км) | 3) 45 + 40 = 85 (км) |
| 4) 45 + 40 = 85 (км) |
Ответ: Через 5 часов расстояние между пешеходами будет 85 км.
Задачи на движение в противоположных направлениях
Урок 32. Решение текстовых задач по математике 1-4 классы
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Задачи на движение в противоположных направлениях»
А давайте с вами заглянем в семью Прошкиных и посмотрим, что у них происходит.
Этого мальчика зовут Денис. Это дедушка Дениса. Интересно, а почему Денис так странно себя ведёт?
– Денис, что случилось? Ты чего ходишь туда сюда?
– Понимаешь, дедушка. Мне в классе нравится одна девочка, Аня. И она попросила, чтобы я научил её решать задачи на движение в противоположных направлениях. А как я могу её научить, если я сам не умею решать такие задачи?
– Как тебе повезло, что у тебя такой умный дедушка. Я, между прочим, увлекаюсь решением задач по математике. Так что своего внука я легко смогу научить решать такие задачи.
Итак, слушай внимательно первую задачу.
Из дома № 75 одновременно вышли два брата-спортсмена и пошли в противоположных направлениях. Скорость движения Лёши 6 км/ч, а Кости – 5 км/ч. На каком расстоянии друг от друга будут братья через 4 часа?
Обрати внимание на слова «в противоположных направлениях». Эти слова говорят о том, что задача на движение в противоположных направлениях.
Давай выполним рисунок к этой задаче.
Точкой обозначим дом, из которого вышли братья, стрелочками укажем направление их движения, а так же укажем скорость их движения.
Чтобы найти расстояние, на котором будут братья через 4 часа, надо знать расстояние, которое пройдёт каждый из них за это время. А ты знаешь, как найти расстояние?
– Знаю, чтобы найти расстояние надо скорость умножить на время.
– Молодец. Правильно. Нам известны скорость, с которой двигался Лёша – 6 км/ч, и время, которое он находился в пути – 4 часа. Значит, мы можем найти расстояние, пройденное Лёшей? Так как мы его найдём?
– Надо его скорость 6 км/ч, умножить на время 4 часа. Получается 24 км прошёл Лёша.
И точно так же мы можем узнать, сколько прошёл его брат, Костя. Его скорость 5 км/ч умножим на время в пути 4 ч. Получается Костя прошёл 20 км.
Ну, узнали мы, сколько прошёл Лёша и Костя, а дальше что?
– А теперь, когда мы знаем, сколько прошёл каждый из братьев отдельно, можем узнать, расстояние между ними.
Ответ: через 4 часа братья будут друг от друга на расстояние 44 километра.
– Ну, мне всё понятно. Я пошёл к Ане, объяснять решение таких задач.
– Подожди. Не торопись. Эту задачу можно решить и другим способом. Вернёмся к нашему рисунку.
Смотри, за один час Лёша отдалился от дома на 6 км, за этот же час Костя отдалился на 5 км. И за это время они отдалились друг от друга на расстояние, равное сумме этих двух чисел. Только это не расстояние. Ведь отдалились они друг от друга за 1 час. Значит, – это скорость их удаления, а точнее, «скорость отдаления» друг от друга.
1) 6 + 5 = 11 (км/ч) – скорость отдаления братьев друг от друга за 1 час
– Ага, если мы знаем, на сколько километров они отдалились друг от друга за 1 час, значит, на сколько они отдалились друг от друга за 4 часа, можно узнать… м–м–м. действием умножения.
Ответ: через 4 часа братья будут друг от друга на расстояние 44 километра.
Я надеюсь, ещё одного способа решения таких задач нет? И я уже могу идти?
– Способов больше нет…. Но я считаю, что учить других ты ещё не готов. Знаешь такую поговорку «Поспешишь – людей насмешишь». Вот попробуй решить такую задачу.
Из центра города Н выехали одновременно в противоположных направлениях король Луи и король Вилли. Средняя скорость автомобиля короля Луи 105 км/ч, а автомобиля короля Вилли – 115 км/ч. Через сколько часов расстояние между королями будет 660 км.
– Что-то я тут опять ничего не понимаю.
– Давай разбираться. Изобразим всё на рисунке.
Точкой обозначим центр города, укажем направление движения и скорости автомобилей королей. Ещё мы знаем, то через некоторое время расстояние между королями будет 660 км. И это время нам надо найти.
– Та-а-ак, наверное, сначала надо всё расстояние разделить на скорость каждого автомобиля.
1) 660 : 115 = ….м–м–м не длится. А-а-а, наверное, надо умножить….
– Подожди, не торопись. Ты сначала хорошо подумай. Обрати внимание на то, что 660 км – это расстояние, которое проехали два автомобиля вместе, а ты собираешься делить по отдельности на скорость первого короля и второго. Если расстояние совместно пройдено, то и скорость должна быть совместная.
Для того чтобы найти время, надо знать расстояние и скорость обоих автомобилей вместе. Мы знаем, что за каждый час один автомобиль отдаляется от города на 105 км, а второй за этого же время – на 115 км. Т.е. они отдаляются за каждый час друг от друга на сумму этих расстояний.
1) 105 + 115 = 220 (км/ч) – скорость отдаления
А раз мы знаем скорость отдаления и всё расстояние пройденное автомобилями, то именно теперь мы можем найти их время в пути. Для этого надо расстояние разделить на скорость отдаления.
2) 660 : 220 = 3 (часа)
Ответ: через 3 часа расстояние между королями будет 660 км.
– А–а–а, теперь я понял свою ошибку. Сначала надо было найти скорость отдаления обоих королей, а затем уже расстояние делить на скорость отдаления.
– Ну, раз ты понял свою ошибку, тогда слушай ещё одну задачу.
От острова одновременно отплыли два корабля в противоположных направлениях. Через 6 часов расстояние между ними было 750 километров. Первый корабль плыл со скоростью 55 км/ч. С какой скоростью плыл второй корабль?
– Да-а-а, интересная задача. Можно я сам попробую её решить.
Я понял, что лучше начать с рисунка – так нагляднее.
Точкой обозначим остров, стрелочками укажем направление движения кораблей. За 6 часов они проплыли 750 километров…
Скорость одного корабля 55 км/ч, а скорость второго корабля мне предстоит узнать.
Та-а-а-ак, чтобы найти скорость второго корабля, надо знать расстояние, которое он проплыл и время, которое он был в пути. Но, мы не знаем, какое расстояние проплыл второй корабль. Нам надо его найти. А как нам его найти? А-а-а. Нам надо знать общее расстояние, и какое расстояние проплыл первый корабль. Общее расстояние мы знаем, а расстояние, которое проплыл первый корабль, мы узнаем, умножив его скорость на время в пути.
1) 55 · 6 = 330 (км) – проплыл первый корабль за 6 часов
Мы знаем всё расстояние и ту его часть, которую проплыл первый корабль. И теперь мы можем узнать, какое расстояние проплыл второй корабль за 6 часов.
2) 750 – 330 = 420 (км) – проплыл второй корабль за 6 часов
Нам известно расстояние, которое проплыл второй корабль и время. Значит, мы легко можем узнать скорость второго корабля. Для этого надо расстояние разделить на время, которое он был в пути.
Ответ: скорость второго корабля 70 км/ч.
Ура! Ура! Я сам решил задачу на движение в противоположных направлениях.
– Ты молодец. Теперь я уверен, что ты готов к тому, чтобы учить других решать подобные задачи. Я горжусь своим внуком.