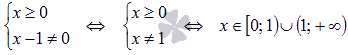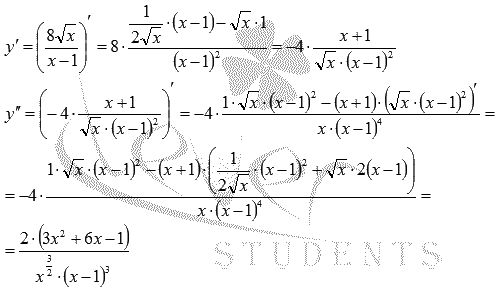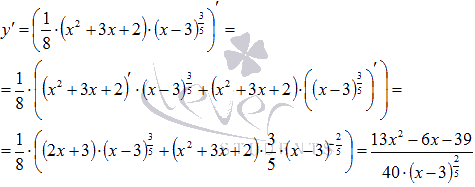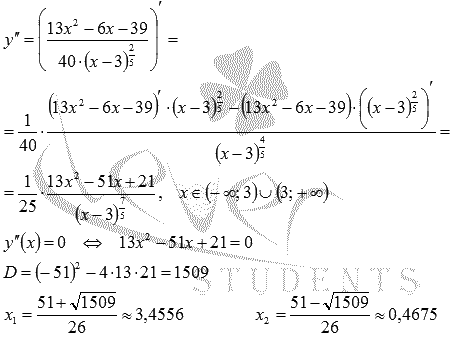что значит выпуклая функция

Выпуклость функции. Направление выпуклости. Точки перегиба. Условия выпуклости и перегиба.

При исследовании функции и построении ее графика на одном из этапов мы определяем точки перегиба и интервалы выпуклости. Эти данные вместе с промежутками возрастания и убывания позволяют схематично представить график исследуемой функции.

Дальнейшее изложение подразумевает, что Вы умеете находить производные функции до некоторого порядка и решать неравенства разных видов.

Изучение материала начнем с необходимых определений и понятий. Далее озвучим связь между значением второй производной функции на некотором интервале и направлением ее выпуклости. После этого перейдем к условиям, которые позводляют определять точки перегиба графика функции. По тексту будем приводить характерные примеры с подробными решениями.

Навигация по странице.

Выпуклость, вогнутость функции, точка перегиба.

Выпуклую вверх функцию часто называют выпуклой, а выпуклую вниз – вогнутой.

Посмотрите на чертеж, иллюстрирующий эти определения.

Другими словами, точка М называется точкой перегиба графика функции, если в этой точке существует касательная и график функции меняет направление выпуклости, проходя через нее.

Если необходимо, обратитесь к разделу касательная к графику функции в точке, чтобы вспомнить условия существования невертикальной и вертикальной касательной.

На рисунке ниже представлены несколько примеров точек перегиба (отмечены красными точками). Заметим, что некоторые функции могут не иметь точек перегиба, а другие могут иметь одну, несколько или бесконечно много точек перегиба.

Нахождение интервалов выпуклости функции.

Сформулируем теорему, которая позволяет определять промежутки выпуклости функции.

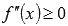
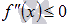
Эта теорема позволяет находитьть промежутки вогнутости и выпуклости функции, нужно лишь на области определения исходной функции решить неравенства и соответственно.

Следует отметить, что точки, в которых функция y=f(x) определена, а вторая производная не существует, будем включать в интервалы вогнутости и выпуклости.

Разберемся с этим на примере.

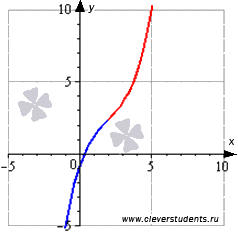
Выяснить промежутки, на которых график функции 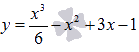имеет выпуклость направленную вверх и выпуклость направленную вниз.

Область определения функции 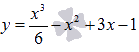— это все множество действительных чисел.

Найдем вторую производную.

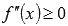
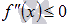
Область определения второй производной совпадает с областью определения исходной функции, поэтому, чтобы выяснить интервалы вогнутости и выпуклости, достаточно решить и соответственно.

Следовательно, функция выпуклая вниз на интервале и выпуклая вверх на интервале .

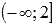
Часть графика функции на интервале выпуклости изображена синим цветом, на интервале вогнутости – красным цветом.

Сейчас рассмотрим пример, когда область определения второй производной не совпадает с областью определения функции. В этом случае, как мы уже отмечали, точки области определения, в которых не существует конечная вторая производная, следует включать в интервалы выпуклости и (или) вогнутости.

Найти промежутки выпуклости и вогнутости графика функции .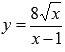

Начнем с области определения функции:

Найдем вторую производную:

Областью определения второй производной является множество 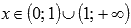. Как видите, x=0 принадлежит области определения исходной функции, но не принадлежит области определения второй производной. Не забывайте про эту точку, ее нужно будет включить в интервал выпуклости и (или) вогнутости.

Таким образом,

и

При график функции имеет выпуклость направленную вниз, при — выпуклость направленную вверх.

Часть графика функции на интервале выпуклости изображена синим цветом, на интервалах вогнутости – красным цветом, черной пунктирной прямой является вертикальная асимптота.

Необходимое и достаточные условия перегиба.

Необходимое условие перегиба.

Сформулируем необходимое условие перегиба графика функции.

Пусть график функции y=f(x) имеет перегиб в точке и имеет при непрерывную вторую производную, тогда выполняется равенство .

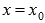
Из этого условия следует, что абсциссы точек перегиба следует искать среди тех, в которых вторая производная функции обращается в ноль. НО, это условие не является достаточным, то есть не все значения , в которых вторая производная равна нулю, являются абсциссами точек перегиба.

Еще следует обратить внимание, что по определению точки перегиба требуется существование касательной прямой, можно и вертикальной. Что это означает? А означает это следующее: абсциссами точек перегиба могут быть все из области определения функции, для которых и . Обычно это точки, в которых знаменатель первой производной обращается в ноль.

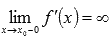
Первое достаточное условие перегиба.

После того как найдены все , которые могут быть абсциссами точек перегиба, следует воспользоваться первым достаточным условием перегиба графика функции.

Пусть функция y=f(x) непрерывна в точке , имеет в ней касательную (можно вертикальную) и эта функция имеет вторую производную в некоторой окрестности точки . Тогда, если в пределах этой окрестности слева и справа от , вторая производная имеет разные знаки, то является точкой перегиба графика функции.

Как видите первое достаточное условие не требует существования второй производной в самой точке , но требует ее существование в окрестности точки .

Сейчас обобщим всю информацию в виде алгоритма.

Алгоритм нахождения точек перегиба функции.

Находим все абсциссы возможных точек перегиба графика функции ( или и ) и выясняем, проходя через какие вторая производная меняет знак. Такие значения и будут абсциссами точек перегиба, а соответствующие им точки будут точками перегиба графика функции.

Рассмотрим два примера нахождения точек перегиба для разъяснения.

Найти точки перегиба и интервалы выпуклости и вогнутости графика функции .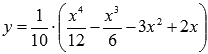

Областью определения функции является все множество действительных чисел.

Найдем первую производную:

Областью определения первой производной также является все множество действительных чисел, поэтому равенства и не выполняется ни для каких .

Найдем вторую производную:

Выясним при каких значениях аргумента x вторая производная обращается в ноль:

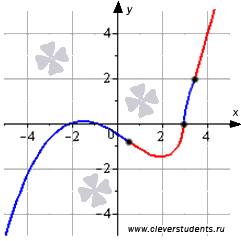
Теперь осталось проверить по достаточному признаку перегиба, в каких из этих точек вторая производная меняет знак. Для этого нанесем точки x=-2 и x=3 на числовую ось и, как в обобщенном методе интервалов, расставим знаки второй производной над каждым промежутком. Под каждым интервалом схематично дугами показано направление выпуклости графика функции.

Взглянув еще раз на числовую ось и знаки второй производной на ее промежутках, можно делать вывод об интервалах выпуклости и вогнутости. График функции выпуклый на интервале 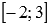и вогнутый на интервалах и .

Часть графика функции на интервале выпуклости изображена синим цветом, на интервалах вогнутости – красным цветом, точки перегиба показаны черными точками.

Найдите абсциссы всех точек перегиба графика функции .

Областью определения данной функции является все множество действительных чисел.

Найдем производную.

Находим вторую производную, область ее определения и точки, в которых она обращается в ноль:

Получили еще две возможные абсциссы точек перегиба. Отмечаем все три точки на числовой прямой и определяем знак второй производной на каждом из полученных интервалов.

Вторая производная меняет знак, проходя через каждую из точек, следовательно, все они являются абсциссами точек перегиба.

Части графика функции на интервалах выпуклости изображены синим цветом, на интервалах вогнутости – красным цветом, точки перегиба показаны черными точками.

Первое достаточное условие перегиба графика функции позволяет определять точки перегиба и не требуют существования второй производной в них. Поэтому, первое достаточное условие можно считать универсальным и самым используемым.

Сейчас сформулируем еще два достаточных условия перегиба, но они применимы лишь при существовании конечной производной в точке перегиба до некоторого порядка.

Второе достаточное условие перегиба.

Выяснить, является ли точка 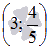точкой перегиба графика функции .

Для начала убедимся, что точка 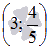принадлежит графику функции:

Функция определена для всех действительных значений аргумента. Найдем первую и вторую производные.

Часть графика функции на интервале выпуклости изображена синим цветом, на интервале вогнутости – красным цветом, точка перегиба показана черной точкой.

Третье достаточное условие перегиба.

Найдите точки перегиба графика функции .

Функция определена на всем множестве действительных чисел.

Таким образом, в точке с абсциссой x=3 может быть перегиб графика функции. Чтобы убедиться в том, что х=3 действительно абсцисса точки перегиба, воспользуемся третьим достаточным условием.

Часть графика функции на интервале выпуклости изображена синим цветом, на интервале вогнутости – красным цветом, точка перегиба показана черной точкой.

Источник

Выпуклость функции

Понятие выпуклости.

Непрерывная функция \(y=f(x)\) называется выпуклой вверх на отрезке \([a,b]\), если для любых точек \(x_<1>\) и \(x_<2>\) отрезка \([a,b]\) выполняется неравенство
$$
f(\frac+x_<2>><2>)\geq\frac)+f(x_<2>)><2>.\label
$$

Дадим геометрическую интерпретацию понятия выпуклости (рис. 20.4). Пусть \(M_<1>,\;M_<2>,\;M_<0>\) — точки графика функции \(y=f(x)\), абсциссы которых равны соответственно \(x_1,\ x_2,\ x_0 = \displaystyle \frac+x_<2>><2>\). Тогда \(\displaystyle \frac)+f(x_<2>)><2>\) есть ордината точки \(К\) — середины отрезка \(M_<1>M_<2>\), а \(f\left(\displaystyle \frac<2>\right)=f(x_0)\) — ордината точки \(M_0\) графика с абсциссой, равной абсциссе точки \(K\).

Рис. 20.4

Условие \eqref означает, что для любых точек \(M_<1>\) и \(M_<2>\) графика функции \(y=f(x)\) середина \(К\) хорды \(M_<1>M_<2>\) или лежит ниже соответствующей точки \(M_0\) графика, или совпадает с точкой \(M_0\).

Если неравенство \eqref является строгим при любых \(x_<1>,\ x_<2>\in[a,b]\) таких, что \(x_<1>\neq x_<2>\), то непрерывную функцию \(y=f(x)\) называют строго выпуклой вверх на отрезке \([a,b]\).

Аналогично, непрерывная функция \(y=f(x)\) называется выпуклой вниз на отрезке \([a,b]\), если для любых точек \(x_<1>\) и \(x_<2>\) отрезка \([a,b]\) выполняется неравенство
$$
f\left(\frac+x_<2>><2>\right)\leq\displaystyle\frac)+f(x_<2>)><2>.\label
$$
Если неравенство \eqref является строгим при любых \(x_<1>,\ x_<2>\in[a,b]\) таких, что \(x_<1>\neq x_<2>\), то непрерывную функцию \(y=f(x)\) называют строго выпуклой вниз на отрезке \([a,b]\).

Функция \(f(x)=x^<2>\) строго выпукла вниз на любом отрезке.

\(\triangle\) В самом деле, при \(x_<1>\neq x_<2>\) неравенство \(\left(\displaystyle \frac+x_<2>><2>\right) 0\). \(\blacktriangle\)

Понятие выпуклости и строгой выпуклости вверх (вниз) можно ввести и на интервале. Например, если неравенство \eqref выполняется для любых точек интервала \((a,b)\), то непрерывная функция \(y=f(x)\) называется выпуклой вверх на этом интервале.

Достаточные условия выпуклости.

Пусть \(f'(x)\) существует на отрезке \([a,b]\), а \(f″(x)\) — на интервале \((a,b)\).

Аналогично, при выполнении на интервале \((a,b)\) условия \(f″(x)\leq 0\) (\(f″(x) Доказательство.

\(\circ\) Ограничимся доказательством для случая, когда выполняется условие \eqref. Нужно доказать, что для любых точек \(x_<1>,\ x_<2>\) отрезка \([a,b]\) выполняется условие \eqref. Пусть, например, \(x_ <1>Замечание 1.

Условие \(f″(x) > 0\) не является необходимым условием строгой выпуклости вниз функции \(y=f(x)\). Например, для функции \(f(x)=x^<4>\) условие \(f″(x) > 0\) нарушается при \(x=0\), так как \(f″(0)=0\), однако эта функция строго выпукла вниз.

Источник

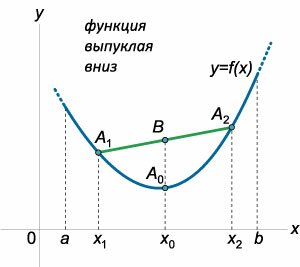
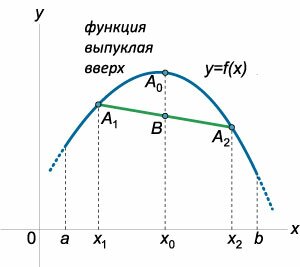
Что значит выпуклая функция

Рассмотрим функцию \(y = f\left( x \right),\) которая предполагается непрерывной на отрезке \(\left[ \right].\) Функция \(y = f\left( x \right)\) называется выпуклой вниз (или просто выпуклой ), если для любых точек \(\) и \(\) из \(\left[ \right]\) выполняется неравенство \[f\left( <\frac<<+ >><2>> \right) \le \frac<> \right) + f\left( <> \right)>><2>.\] Если данное неравенство является строгим при любых \(, \in \left[ \right],\) таких, что \( \ne ,\) то функцию \(f\left( x \right)\) называют строго выпуклой вниз на отрезке \(\left[ \right].\)

Аналогично определяется выпуклая вверх функция. Функция \(f\left( x \right)\) называется выпуклой вверх (или вогнутой ), если для любых точек \(\) и \(\) отрезка \(\left[ \right]\) справедливо неравенство \[f\left( <\frac<<+ >><2>> \right) \ge \frac<> \right) + f\left( <> \right)>><2>.\] Если это неравенство является строгим при любых \(, \in \left[ \right],\) таких, что \( \ne ,\) то функцию \(f\left( x \right)\) называют строго выпуклой вверх на отрезке \(\left[ \right].\)

Для функции, выпуклой вниз (рисунок \(1\)), середина \(B\) любой хорды \(\) лежит выше соответствующей точки \(\) графика функции или совпадает с этой точкой.

Аналогично, для функции, выпуклой вверх (рисунок \(2\)), середина \(B\) любой хорды \(\) лежит ниже соответствующей точки \(\) графика функции или совпадает с этой точкой.

Выпуклые функции обладают еще одним наглядным свойством, которое связано с расположением касательной к графику функции. Функция \(f\left( x \right)\) является выпуклой вниз на отрезке \(\left[ \right]\) тогда и только тогда, когда ее график лежит не ниже касательной проведенной к нему в любой точке \(\) отрезка \(\left[ \right]\) (рисунок \(3\)).

Если \(f»\left( x \right) \ge 0\) при всех \(x \in \left( \right),\) то функция \(f\left( x \right)\) выпукла вниз на отрезке \(\left[ \right];\)

Если \(f»\left( x \right) \le 0\) при всех \(x \in \left( \right),\) то функция \(f\left( x \right)\) выпукла вверх на отрезке \(\left[ \right].\)

В тех случаях, когда вторая производная строго больше (меньше) нуля, говорят, соответственно, о строгой выпуклости вниз (или вверх ).

Отметим, что необходимое условие выпуклости функции (т.е. прямая теорема, в которой, к примеру, из условия выпуклости вниз следует, что \(f»\left( x \right) \ge 0\)) выполняется лишь для нестрогого неравенства. В случае строгой выпуклости необходимое условие, вообще говоря, не соблюдается. Например, функция \(f\left( x \right) = \) является строго выпуклой вниз. Однако в точке \(x = 0\) ее вторая производная равна нулю, т.е. строгое неравенство \(f»\left( x \right) \gt 0\) в этом случае не выполняется.

Если функции \(f\) и \(g\) выпуклы вниз (вверх), то любая их линейная комбинация \(af + bg,\) где \(a\), \(b\) − положительные действительные числа, также выпукла вниз (вверх).

Если функция \(u = g\left( x \right)\) выпукла вниз, а функция \(y = f\left( u \right)\) является выпуклой вниз и неубывающей, то сложная функция \(y = f\left( \right)\) будет также выпуклой вниз.

Если функция \(u = g\left( x \right)\) выпукла вверх, а функция \(y = f\left( u \right)\) является выпуклой вниз и невозрастающей, то сложная функция \(y = f\left( \right)\) будет выпуклой вниз.

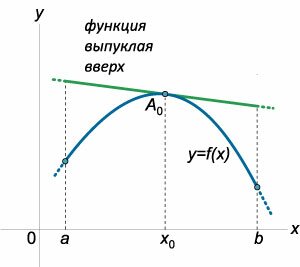
Локальный максимум выпуклой вверх функции, заданной на отрезке \(\left[ \right],\) является одновременно ее наибольшим значением на этом отрезке.

Локальный минимум выпуклой вниз функции, заданной на отрезке \(\left[ \right],\) является одновременно ее наименьшим значением на этом отрезке.

Ясно, что полное число возможных комбинаций трех величин с различными знаками равно \(8\). Эскизы соответствующих графиков функций показаны на рисунке \(5\).

Таким образом, исходя из знака второй производной, устанавливаем, что заданная функция

Источник