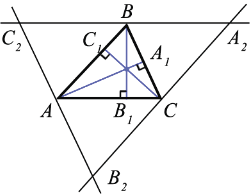
Докажите что прямые содержащие высоты треугольника пересекаются в одной точке

Теорема о пересечении высот треугольника

Теорема

Доказательство

Доказать: АА₁, ВВ₁ и СС₁ пересекаются в одной точке.

Доказательство:

Проведём через каждую вершину АВС прямую, параллельную противоположной стороне.

Получим А₂В₂С₂. Точки А, В и С являются серединами сторон этого треугольника. Действительно, АВ = А₂С и АВ = СВ₂ как противоположные стороны параллелограммов АВА₂С и АВСВ₂, поэтому А₂С = СВ₂. Аналогично С₂А = АВ₂ и С₂В = ВА₂. Кроме того, как следует из построения, СС₁А₂В₂, АА₁В₂С₂ и ВВ₁А₂С₂. Таким образом, прямые АА₁, ВВ₁ и СС₁ являются серединными перпендикулярами к сторонам треугольника А₂В₂С₂. Следовательно, они пересекаются в одной точке. Теорема доказана.

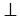
Замечательные точки треугольника : точка пересечения медиан, точка пересечения биссектрис, точка пересечения серединных перпендикуляров к сторонам и точка пересечения высот (или их продолжений).

Поделись с друзьями в социальных сетях:

Источник

Докажите, что прямые, содержащие высоты треугольника, пересекаются в одной точке.

Через вершины данного треугольника провёдем прямые, параллельные противолежащим сторонам. Рассмотрим треугольник с вершинами в точках пересечения проведённых прямых. Высоты исходного треугольника лежат на серединных перпендикулярах построенного. Поэтому они пересекаются в одной точке.

Если треугольник остроугольный, то его высоты лежат на биссектрисах треугольника с вершинами в основаниях высот данного (ортотреугольник), и поэтому пересекаются в одной точке.

Если же треугольник тупоугольный, то одна его высота лежит на биссектрисе одного из углов ортотреугольника, а две другие — на биссектрисах внешних углов ортотреугольника.

Для прямоугольного треугольника утверждение очевидно.

Если треугольник остроугольный, то его высоты лежат на биссектрисах треугольника с вершинами в точках пересечения с описанной окружностью продолжений высот данного треугольника.

Пусть AA₁, BB₁, CC₁ — высоты треугольника ABC. Обозначим через , , углы треугольника ABC. Тогда из прямоугольного треугольника AB₁B находим, что

AB₁ = AB| cos|.

AС₁ = AС| cos|, BA₁ = AB| cos|, BC₁ = BC| cos|,

CA₁ = CA| cos|, CB₁ = CB| cos|.

(Если треугольник остроугольный, то знаки модуля можно опустить). Поэтому

. . =

= = 1.

Тогда по теореме Чевы прямые AA₁, BB₁ и CC₁ пересекаются в одной точке.

Пусть H — точка пересечения высот BB₁ и CC₁ треугольника ABC. Тогда

Сложив почленно эти равенства, получим, что

Следовательно, прямая AH перпендикулярна стороне BC.

Пусть O — центр описанной окружности треугольника ABC. Рассмотрим вектор = + + . Если

+ = ,

то K — вершина ромба AOBK. Значит, OK AB. Если

= + ,

то CHOK. Значит, CH AB. Поэтому точка H лежит на прямой, содержащей высоту треугольника ABC, проведённую из вершины C.

Аналогично докажем, что точка H (конец вектора ) лежит на прямых, содержащих две другие высоты треугольника. Следовательно, все три прямые пересекаются в точке H.

Воспользуемся следующим утверждением. Если A, B, C и H — произвольные точки плоскости, то

. + . + . = 0.

Пусть прямые, содержащие высоты треугольника ABC, проведённые из вершин A и B, пересекаются в точке H. Тогда AH BC и BH AC, поэтому

. = 0, . = 0.

Из приведённого выше утверждения следует, что

. = 0.

Значит, CH AB, т.е. прямая, содержащая высоту, проведённую из вершины C, также проходит через точку H.

Другие доказательства: см. МШ, N1, 1988, с.72, В.В.Прасолов, «Несколько доказательств теоремы о высотах треугольника».

Источник

Теорема о пересечении высот треугольника

Мы доказали, что биссектрисы треугольника пересекаются в одной точке, серединные перпендикуляры к сторонам треугольника пересекаются в одной точке. Ранее было доказано, что медианы треугольника пересекаются в одной точке (п. 64). Оказывается, аналогичным свойством обладают и высоты треугольника.

Рассмотрим произвольный треугольник АВС и докажем, что прямые АА₁ ВВ₁ и СС₁ содержащие его высоты, пересекаются в одной точке (рис. 229).

Проведём через каждую вершину треугольника АВС прямую, параллельную противоположной стороне. Получим треугольник А₂В₂С₂. Точки А, В и С являются серединами сторон этого треугольника. Действительно, АВ = А₂С и АВ = СВ₂ как противоположные стороны параллелограммов АВА₂С и АВСВ₂, поэтому А₂С = СВ₂. Аналогично С₂А = АВ₂ и С₂В = ВА₂. Кроме того, как следует из построения, СС₁ ⊥ А₂В₂, АА₁ ⊥ В₂С₂ и ВВ₁ ⊥ А₂С₂. Таким образом, прямые АА₁, ВВ₁ и СС₁ являются серединными перпендикулярами к сторонам треугольника А₂В₂С₂. Следовательно, оНи пересекаются в одной точке. Теорема доказана.

Итак, с каждым треугольником связаны четыре точки: точка пересечения медиан, точка пересечения биссектрис, точка пересечения серединных перпендикуляров к сторонам и точка пересечения высот (или их продолжений). Эти четыре точки называются замечательными точками треугольника.

Источник

Докажите что прямые содержащие высоты треугольника пересекаются в одной точке

дПЛБЦЙФЕ, ЮФП РТСНЩЕ, УПДЕТЦБЭЙЕ ЧЩУПФЩ ФТЕХЗПМШОЙЛБ, РЕТЕУЕЛБАФУС Ч ПДОПК ФПЮЛЕ.

рПДУЛБЪЛБ

тБУУНПФТЙФЕ ФТЕХЗПМШОЙЛ, ПВТБЪПЧБООЩК РТСНЩНЙ, РТПЧЕДЈООЩНЙ ЮЕТЕЪ ЧЕТЫЙОЩ ДБООПЗП РБТБММЕМШОП РТПФЙЧПМЕЦБЭЙН УФПТПОБН.

тЕЫЕОЙЕ

юЕТЕЪ ЧЕТЫЙОЩ ДБООПЗП ФТЕХЗПМШОЙЛБ РТПЧЈДЕН РТСНЩЕ, РБТБММЕМШОЩЕ РТПФЙЧПМЕЦБЭЙН УФПТПОБН. тБУУНПФТЙН ФТЕХЗПМШОЙЛ У ЧЕТЫЙОБНЙ Ч ФПЮЛБИ РЕТЕУЕЮЕОЙС РТПЧЕДЈООЩИ РТСНЩИ. чЩУПФЩ ЙУИПДОПЗП ФТЕХЗПМШОЙЛБ МЕЦБФ ОБ УЕТЕДЙООЩИ РЕТРЕОДЙЛХМСТБИ РПУФТПЕООПЗП. рПЬФПНХ ПОЙ РЕТЕУЕЛБАФУС Ч ПДОПК ФПЮЛЕ.

еУМЙ ФТЕХЗПМШОЙЛ ПУФТПХЗПМШОЩК, ФП ЕЗП ЧЩУПФЩ МЕЦБФ ОБ ВЙУУЕЛФТЙУБИ ФТЕХЗПМШОЙЛБ У ЧЕТЫЙОБНЙ Ч ПУОПЧБОЙСИ ЧЩУПФ ДБООПЗП (ПТФПФТЕХЗПМШОЙЛ), Й РПЬФПНХ РЕТЕУЕЛБАФУС Ч ПДОПК ФПЮЛЕ.

еУМЙ ЦЕ ФТЕХЗПМШОЙЛ ФХРПХЗПМШОЩК, ФП ПДОБ ЕЗП ЧЩУПФБ МЕЦЙФ ОБ ВЙУУЕЛФТЙУЕ ПДОПЗП ЙЪ ХЗМПЧ ПТФПФТЕХЗПМШОЙЛБ, Б ДЧЕ ДТХЗЙЕ — ОБ ВЙУУЕЛФТЙУБИ ЧОЕЫОЙИ ХЗМПЧ ПТФПФТЕХЗПМШОЙЛБ.

дМС РТСНПХЗПМШОПЗП ФТЕХЗПМШОЙЛБ ХФЧЕТЦДЕОЙЕ ПЮЕЧЙДОП.

еУМЙ ФТЕХЗПМШОЙЛ ПУФТПХЗПМШОЩК, ФП ЕЗП ЧЩУПФЩ МЕЦБФ ОБ ВЙУУЕЛФТЙУБИ ФТЕХЗПМШОЙЛБ У ЧЕТЫЙОБНЙ Ч ФПЮЛБИ РЕТЕУЕЮЕОЙС У ПРЙУБООПК ПЛТХЦОПУФША РТПДПМЦЕОЙК ЧЩУПФ ДБООПЗП ФТЕХЗПМШОЙЛБ.

(еУМЙ ФТЕХЗПМШОЙЛ ПУФТПХЗПМШОЩК, ФП ЪОБЛЙ НПДХМС НПЦОП ПРХУФЙФШ). рПЬФПНХ

уМПЦЙЧ РПЮМЕООП ЬФЙ ТБЧЕОУФЧБ, РПМХЮЙН, ЮФП

йЪ РТЙЧЕДЈООПЗП ЧЩЫЕ ХФЧЕТЦДЕОЙС УМЕДХЕФ, ЮФП

дТХЗЙЕ ДПЛБЪБФЕМШУФЧБ: УН. ны, N1, 1988, У.72, ч.ч.рТБУПМПЧ, «оЕУЛПМШЛП ДПЛБЪБФЕМШУФЧ ФЕПТЕНЩ П ЧЩУПФБИ ФТЕХЗПМШОЙЛБ».

Источник

Высоты в остроугольном треугольнике

В любом треугольнике все три высоты пересекаются в одной точке. Все высоты в остроугольном треугольнике лежат внутри треугольника (как и точка пересечения высот).

Высоты BB₁ и CC₁ остроугольного треугольника ABC пересекаются в точке E. Доказать, что углы BB₁C₁ и BCC₁ равны; углы B₁C₁С и BB₁C равны.

Дано: ΔABC — остроугольный,

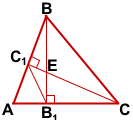
Около любого треугольника можно описать окружность. Центр окружности, описанной около прямоугольного треугольника, лежит на середине его гипотенузы. Радиус такой окружности равен половине гипотенузы.

Центр описанной около прямоугольного треугольника BB₁C окружности лежит на середине гипотенузы BC, радиус этой окружности равен половине BC.

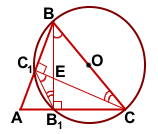
Центр описанной около прямоугольного треугольника BCC₁ окружности — середина гипотенузы BC, радиус равен половине BC.

Значит эти треугольники вписаны в одну и ту же окружность.

Следовательно, точки B, C, B₁ и C₁лежат на одной окружности.

∠B₁C₁С=∠B₁BC (как вписанные углы, опирающиеся на одну дугу B₁C).

Что и требовалось доказать.

То есть решение такого рода задач начинаем с поиска прямоугольных треугольников с общей гипотенузой.

2 Comments

Здравствуйте!
во втором случае: Угол ВВ1С — прямой, имелся в виду угол В1ВС, как опирающийся на дугу В1С

Источник