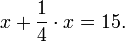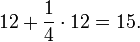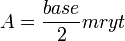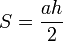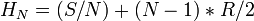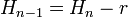Информацию о чем содержит в себе древнеегипетский папирус ринда
Папирус Ринда
Математический папирус Ахмеса (также известен как папирус Ринда или папирус Райнда) — древнеегипетское учебное руководство по арифметике и геометрии периода Среднего царства, переписанное ок. 1650 до н. э. писцом по имени Ахмес на свиток папируса длиной 5,25 м. и шириной 33 см.
Папирус Ахмеса был обнаружен в 1858 и часто называется папирусом Райнда по имени его первого владельца. В 1870 папирус был расшифрован, переведён и издан. Ныне большая часть рукописи находится в Британском музее в Лондоне, а вторая часть — в Нью-Йорке.
Содержание
Проблемы папируса Ахмеса (Ринда)
Папирус Ахмеса включает условия и решения 84 задач и является наиболее полным египетским задачником, дошедшим до наших дней. Московский математический папирус, находящийся в Государственном музее изобразительных искусств имени А. С. Пушкина, уступает папирусу Ахмеса по полноте (он состоит из 25 задач), но превосходит его по возрасту. Установлено, что оригинал, с которого был переписан папирус Ахмеса, относится ко второй половине XIX века до н. э.; имя его автора неизвестно. Отдельные исследователи предполагают, что он мог быть составлен на основании ещё более древнего текста III тысячелетия до н. э.
Во вступительной части папируса Райнда объясняется, что он посвящён «совершенному и основательному исследованию всех вещей, пониманию их сущности, познанию их тайн». Все задачи, приведённые в тексте, имеют в той или другой степени практический характер и могли быть применены в строительстве, размежевании земельных наделов и других сферах жизни и производства. По преимуществу это задачи на нахождение площадей треугольника, четырёхугольников и круга, разнообразные действия с целыми числами и аликвотными дробями, пропорциональное деление, нахождение отношений. Для решения многих из них вырабатывались общие правила.
Вместе с тем, в папирусе есть целый ряд свидетельств того, что математика в Древнем Египте переросла исключительно практическую стадию и приобрела теоретический характер. Так, египетские математики умели брать корень и возводить в степень, были знакомы с арифметической и геометрической прогрессией (одна из задач папируса Ахмеса сводится к нахождению суммы членов геометрической прогрессии). Множество задач, сводящихся к решению уравнений (в том числе квадратных) с одним неизвестным, связаны употреблением специального иероглифа «куча» (аналога латинского x, традиционно употребляемого в современной алгебре) для обозначения неизвестного, что указывает на оформление зачатков алгебры.
Папирус Райнда, как и Московский математический папирус, показывает, что древние египтяне с лёгкостью справлялись с измерением площади треугольника и относительно точно определяли приближение числа 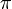
Проблема № R26 Папируса Ринда
Неизвестное число (‘ḥ‘) складывается с 1/4, которое также содержит ‘ḥ‘, и получается 15, т.е.
Первый шаг: древний математик подставляет вместо «х» 4. Очевидно, что это число не подходит для решения, 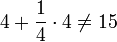
| ✔ | 1 | 4 |
| ✔ | 1/4 | 1 |
| 1 + 1/4 | 5 |
| ✔ | 1 | 5 |
| ✔ | 2 | 10 |
| 3 | 15 |
Третий шаг: вычислим 4 x 3 :
| 1 | 3 | |
| 2 | 6 | |
| ✔ | 4 | 12 |
| 4 | 12 |
Четвертый шаг: Проверим результаты наших вычислений, т.е.
| ✔ | 1 | 12 |
| ✔ | 1/4 | 3 |
| 1 + 1/4 | 15 |
Искомое число ‘ḥ‘ равно 12.
Проблема № R44 Папируса Ринда
Проблема № R44 Папируса Ринда свидетельствует, что египтяне знали формулу для нахождения объема куба: 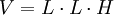
Проблема № R48 Папируса Ринда
| ✔ | 1 | 9 setjat |
| 2 | 18 setjat | |
| 4 | 36 setjat | |
| ✔ | 8 | 72 setjat |
| 81 |
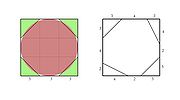
Сложность этой задачи заключается в том, что к ней не содержится ни каких поясняющих текстов. Перед нами только две таблицы цифр и один рисунок. На рисунке изображена фигура напоминающая восьмиугольник или окружность и вписанная в квадрат.
Вторая теория, предложенная Michel Guillemot, более точно объясняет рисунок. Теория утверждает, что на рисунке изображен неправильный восьмиугольник, чья площадь должна быть равна вписанному в квадрат кругу. Площадь такого восьмиугольника ищется по формуле: 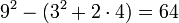
Людвиг Борхардт нашел очень похожий рисунок на стенах храма в Луксоре.
Проблема № R50 Папируса Ринда
«После вычитания получается 8».
| 1 х 8 | = 8 | |
| 2 х 8 | = 16 | |
| 4 х 8 | = 32 | |
| ✔ | 8 х 8 | = 64 |
«Площадь круга составляет 64».
Проблема № R51 Папируса Ринда
Формула египтян идентична современной:
Проблема № R52 Папируса Ринда
Проблема R52 Папируса Ринда посвящена вычислению площади трапеции.
| 1 х 1000 | = 1000 | |
| 1/2 х 1000 | = 500 | |
| ✔ | 1 х 1000 | = 2000 |
| 2 х 1000 | = 4000 | |
| ✔ | 4 х 1000 | = 8000 |
| 10000 (т.е. 100 setjat) |
Это решение можно записать следующей формулой: 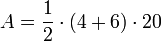
Проблема № R56 Папируса Ринда
Проблемы R56, R57, R58 и R59 Папируса Ринда подробно рассматривают способы вычисления наклона пирамиды.
Древнеегипетский термин «секед» обозначал угол наклона. Он находился через высоту, разделенную на половину основания.
Наклон равен 5 1 /25 ладоней.
В общем виде египетская формула вычисления секеда пирамиды выглядит так: 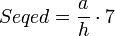
Проблема № R64 Папируса Ринда
Проблема № R64 Папируса Ринда говорит нам о том, что в Древнем Египте применялась в вычислениях арифметическая прогрессия.
 | «Пример разделения на части. Если кто-то говорит вам: у нас есть 10 héqat пшеницы на 10 человек, но есть разница между ними в 1/8 héqat пшеницы. В среднем это 1 héqat. Вычитаем 1 из 10, получаем 9. Возьмем половину от разницы, т.е. 1/16. Умножим на 9. Далее 1/2 и 1/16 héqat прибавим к среднему значению и вычтем 1/8 héqat у каждого последующего человека. Вот расчеты того, о чем с вами говорим: «. |  |
| 1 1/2 1/16 |
| 1 1/4 1/8 1/16 |
| 1 1/4 1/16 |
| 1 1/8 1/16 |
| 1 1/16 |
| 1/2 1/4 1/8 1/16 |
| 1/2 1/4 1/16 |
| 1/2 1/8 1/16 |
| 1/2 1/16 |
| 1/4 1/8 1/16 |
| 10 |
Находим среднее количество héqat, которое раздается каждому, т.е. S/N = 10/10 = 1.
Затем вычислим ту разницу, которая получается при последующем делении. Т.е. N-1 = 10-1, равно 9. Таким образом R/2 = 1/16, а R/2 * (N-1) = 1/16 * 9 = 1/2 + 1/16. Самое большое количество вычисляется по формуле: R/2 * (N-1) + S/N = 1/2 + 1/16 + 1.
Распределение на 10 частей :
Вполне возможно решение этой задачи имело практическое применение.
Можно записать решение в виде формул:
Проблема № R79 Папируса Ринда
Проблема № R79 Папируса Ринда говорит нам о том, что в Древнем Египте применялась в вычислениях геометрическая прогрессия. Впрочем нам известно только то, что египтяне использовали для прогрессии числа «2» и «1/2», т.е. могли получать такие значения как: 1/2, 1/4, 1/8. и 2, 4, 8, 16. Так же остается открытым вопрос о практическом использовании геометрической прогрессии в Древнем Египте.
| ✔ | 1 | 2801 |
| ✔ | 2 | 5602 |
| ✔ | 4 | 11204 |
| 7 | 19607 |
| Домов | 7 |
| Кошек | 49 |
| Мышей | 343 |
| Солод | 2401 (писец по ошибке написал 2301) |
| Héqat | 16807 |
| 19607 |
См. также
Примечания
Литература
Полезное
Смотреть что такое «Папирус Ринда» в других словарях:
Папирус Ринда — см. Ахмеса папирус (Источник: «Древнеегипетский словарь справочник».) … Энциклопедия мифологии
Математический папирус Ринда — Папирус Ахмеса Часть папируса Ахмеса Математический папирус Ахмеса (также известен как папирус Ринда или папирус Райнда) древнеегипетское учебное руководство по арифметике и геометрии периода Среднего царства, переписанное ок. 1650 до н. э.… … Википедия
Папирус Райнда — Папирус Ахмеса Часть папируса Ахмеса Математический папирус Ахмеса (также известен как папирус Ринда или папирус Райнда) древнеегипетское учебное руководство по арифметике и геометрии периода Среднего царства, переписанное ок. 1650 до н. э.… … Википедия
Ринда папирус — Папирус Ахмеса Часть папируса Ахмеса Математический папирус Ахмеса (также известен как папирус Ринда или папирус Райнда) древнеегипетское учебное руководство по арифметике и геометрии периода Среднего царства, переписанное ок. 1650 до н. э.… … Википедия
Папирус Ахмеса — Часть папируса Ахмеса Математический папирус Ахмеса (также известен как папирус Ринда или папирус Райнда) древнеегипетское учебное руководство по арифметике … Википедия
Папирус — (Cyperus Papyrus L., иначе Papyrus antiquorum Willd.) многолетнее травянистое растение из семейства осоковых (Cyperaceae). П. растет по берегам рек и болот Северной Африки и на острове Сицилии, на почве, богатой илом. В почве укореняются толстые … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Ринда папирус — древнеегипетская математическая рукопись, хранящаяся в Британском музее (Лондон); Р. п. назван по имени его владельца английского египтолога А. Г. Ринда (А. Н. Rhind). См. Папирусы математические … Большая советская энциклопедия
Ринда папирус — см. Папирус … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Ахмеса папирус — папирус Ринда др. егип. математич. рукопись … Древний мир. Энциклопедический словарь
Московский математический папирус — Четырнадцатая проблема Московского математического папируса (Struve 1930) Московский математический папирус («математический папирус Голенищева») один из древнейших известных современности математических текстов. Он был составлен около 1850 … Википедия
Ринда папирус
Математический папирус Ахмеса (также известен как папирус Ринда или папирус Райнда) — древнеегипетское учебное руководство по арифметике и геометрии периода Среднего царства, переписанное ок. 1650 до н. э. писцом по имени Ахмес на свиток папируса длиной 5,25 м. и шириной 33 см.
Папирус Ахмеса был обнаружен в 1858 и часто называется папирусом Райнда по имени его первого владельца. В 1870 папирус был расшифрован, переведён и издан. Ныне большая часть рукописи находится в Британском музее в Лондоне, а вторая часть — в Нью-Йорке.
Содержание
Проблемы папируса Ахмеса (Ринда)
Папирус Ахмеса включает условия и решения 84 задач и является наиболее полным египетским задачником, дошедшим до наших дней. Московский математический папирус, находящийся в Государственном музее изобразительных искусств имени А. С. Пушкина, уступает папирусу Ахмеса по полноте (он состоит из 25 задач), но превосходит его по возрасту. Установлено, что оригинал, с которого был переписан папирус Ахмеса, относится ко второй половине XIX века до н. э.; имя его автора неизвестно. Отдельные исследователи предполагают, что он мог быть составлен на основании ещё более древнего текста III тысячелетия до н. э.
Во вступительной части папируса Райнда объясняется, что он посвящён «совершенному и основательному исследованию всех вещей, пониманию их сущности, познанию их тайн». Все задачи, приведённые в тексте, имеют в той или другой степени практический характер и могли быть применены в строительстве, размежевании земельных наделов и других сферах жизни и производства. По преимуществу это задачи на нахождение площадей треугольника, четырёхугольников и круга, разнообразные действия с целыми числами и аликвотными дробями, пропорциональное деление, нахождение отношений. Для решения многих из них вырабатывались общие правила.
Вместе с тем, в папирусе есть целый ряд свидетельств того, что математика в Древнем Египте переросла исключительно практическую стадию и приобрела теоретический характер. Так, египетские математики умели брать корень и возводить в степень, были знакомы с арифметической и геометрической прогрессией (одна из задач папируса Ахмеса сводится к нахождению суммы членов геометрической прогрессии). Множество задач, сводящихся к решению уравнений (в том числе квадратных) с одним неизвестным, связаны употреблением специального иероглифа «куча» (аналога латинского x, традиционно употребляемого в современной алгебре) для обозначения неизвестного, что указывает на оформление зачатков алгебры.
Папирус Райнда, как и Московский математический папирус, показывает, что древние египтяне с лёгкостью справлялись с измерением площади треугольника и относительно точно определяли приближение числа 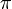
Проблема № R26 Папируса Ринда
Неизвестное число (‘ḥ‘) складывается с 1/4, которое также содержит ‘ḥ‘, и получается 15, т.е.
Первый шаг: древний математик подставляет вместо «х» 4. Очевидно, что это число не подходит для решения, 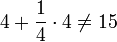
| ✔ | 1 | 4 |
| ✔ | 1/4 | 1 |
| 1 + 1/4 | 5 |
| ✔ | 1 | 5 |
| ✔ | 2 | 10 |
| 3 | 15 |
Третий шаг: вычислим 4 x 3 :
| 1 | 3 | |
| 2 | 6 | |
| ✔ | 4 | 12 |
| 4 | 12 |
Четвертый шаг: Проверим результаты наших вычислений, т.е.
| ✔ | 1 | 12 |
| ✔ | 1/4 | 3 |
| 1 + 1/4 | 15 |
Искомое число ‘ḥ‘ равно 12.
Проблема № R44 Папируса Ринда
Проблема № R44 Папируса Ринда свидетельствует, что египтяне знали формулу для нахождения объема куба: 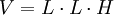
Проблема № R48 Папируса Ринда
| ✔ | 1 | 9 setjat |
| 2 | 18 setjat | |
| 4 | 36 setjat | |
| ✔ | 8 | 72 setjat |
| 81 |
Сложность этой задачи заключается в том, что к ней не содержится ни каких поясняющих текстов. Перед нами только две таблицы цифр и один рисунок. На рисунке изображена фигура напоминающая восьмиугольник или окружность и вписанная в квадрат.
Вторая теория, предложенная Michel Guillemot, более точно объясняет рисунок. Теория утверждает, что на рисунке изображен неправильный восьмиугольник, чья площадь должна быть равна вписанному в квадрат кругу. Площадь такого восьмиугольника ищется по формуле: 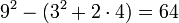
Людвиг Борхардт нашел очень похожий рисунок на стенах храма в Луксоре.
Проблема № R50 Папируса Ринда
«После вычитания получается 8».
| 1 х 8 | = 8 | |
| 2 х 8 | = 16 | |
| 4 х 8 | = 32 | |
| ✔ | 8 х 8 | = 64 |
«Площадь круга составляет 64».
Проблема № R51 Папируса Ринда
Формула египтян идентична современной:
Проблема № R52 Папируса Ринда
Проблема R52 Папируса Ринда посвящена вычислению площади трапеции.
| 1 х 1000 | = 1000 | |
| 1/2 х 1000 | = 500 | |
| ✔ | 1 х 1000 | = 2000 |
| 2 х 1000 | = 4000 | |
| ✔ | 4 х 1000 | = 8000 |
| 10000 (т.е. 100 setjat) |
Это решение можно записать следующей формулой: 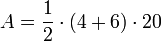
Проблема № R56 Папируса Ринда
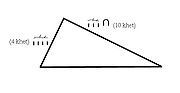
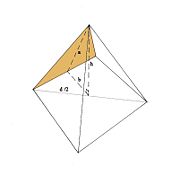
Проблемы R56, R57, R58 и R59 Папируса Ринда подробно рассматривают способы вычисления наклона пирамиды.
Древнеегипетский термин «секед» обозначал угол наклона. Он находился через высоту, разделенную на половину основания.
Наклон равен 5 1 /25 ладоней.
В общем виде египетская формула вычисления секеда пирамиды выглядит так: 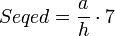
Проблема № R64 Папируса Ринда
Проблема № R64 Папируса Ринда говорит нам о том, что в Древнем Египте применялась в вычислениях арифметическая прогрессия.
 | «Пример разделения на части. Если кто-то говорит вам: у нас есть 10 héqat пшеницы на 10 человек, но есть разница между ними в 1/8 héqat пшеницы. В среднем это 1 héqat. Вычитаем 1 из 10, получаем 9. Возьмем половину от разницы, т.е. 1/16. Умножим на 9. Далее 1/2 и 1/16 héqat прибавим к среднему значению и вычтем 1/8 héqat у каждого последующего человека. Вот расчеты того, о чем с вами говорим: «. |  |
| 1 1/2 1/16 |
| 1 1/4 1/8 1/16 |
| 1 1/4 1/16 |
| 1 1/8 1/16 |
| 1 1/16 |
| 1/2 1/4 1/8 1/16 |
| 1/2 1/4 1/16 |
| 1/2 1/8 1/16 |
| 1/2 1/16 |
| 1/4 1/8 1/16 |
| 10 |
Находим среднее количество héqat, которое раздается каждому, т.е. S/N = 10/10 = 1.
Затем вычислим ту разницу, которая получается при последующем делении. Т.е. N-1 = 10-1, равно 9. Таким образом R/2 = 1/16, а R/2 * (N-1) = 1/16 * 9 = 1/2 + 1/16. Самое большое количество вычисляется по формуле: R/2 * (N-1) + S/N = 1/2 + 1/16 + 1.
Распределение на 10 частей :
Вполне возможно решение этой задачи имело практическое применение.
Можно записать решение в виде формул:
Проблема № R79 Папируса Ринда
Проблема № R79 Папируса Ринда говорит нам о том, что в Древнем Египте применялась в вычислениях геометрическая прогрессия. Впрочем нам известно только то, что египтяне использовали для прогрессии числа «2» и «1/2», т.е. могли получать такие значения как: 1/2, 1/4, 1/8. и 2, 4, 8, 16. Так же остается открытым вопрос о практическом использовании геометрической прогрессии в Древнем Египте.
| ✔ | 1 | 2801 |
| ✔ | 2 | 5602 |
| ✔ | 4 | 11204 |
| 7 | 19607 |
| Домов | 7 |
| Кошек | 49 |
| Мышей | 343 |
| Солод | 2401 (писец по ошибке написал 2301) |
| Héqat | 16807 |
| 19607 |
См. также
Примечания
Литература
Полезное
Смотреть что такое «Ринда папирус» в других словарях:
Ринда папирус — древнеегипетская математическая рукопись, хранящаяся в Британском музее (Лондон); Р. п. назван по имени его владельца английского египтолога А. Г. Ринда (А. Н. Rhind). См. Папирусы математические … Большая советская энциклопедия
Ринда папирус — см. Папирус … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Папирус Райнда — Папирус Ахмеса Часть папируса Ахмеса Математический папирус Ахмеса (также известен как папирус Ринда или папирус Райнда) древнеегипетское учебное руководство по арифметике и геометрии периода Среднего царства, переписанное ок. 1650 до н. э.… … Википедия
Папирус Ринда — Папирус Ахмеса Часть папируса Ахмеса Математический папирус Ахмеса (также известен как папирус Ринда или папирус Райнда) древнеегипетское учебное руководство по арифметике и геометрии периода Среднего царства, переписанное ок. 1650 до н. э.… … Википедия
Папирус Ахмеса — Часть папируса Ахмеса Математический папирус Ахмеса (также известен как папирус Ринда или папирус Райнда) древнеегипетское учебное руководство по арифметике … Википедия
Папирус Ринда — см. Ахмеса папирус (Источник: «Древнеегипетский словарь справочник».) … Энциклопедия мифологии
Папирус — (Cyperus Papyrus L., иначе Papyrus antiquorum Willd.) многолетнее травянистое растение из семейства осоковых (Cyperaceae). П. растет по берегам рек и болот Северной Африки и на острове Сицилии, на почве, богатой илом. В почве укореняются толстые … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Математический папирус Ринда — Папирус Ахмеса Часть папируса Ахмеса Математический папирус Ахмеса (также известен как папирус Ринда или папирус Райнда) древнеегипетское учебное руководство по арифметике и геометрии периода Среднего царства, переписанное ок. 1650 до н. э.… … Википедия
Ахмеса папирус — Ринда папирус, древнеегипетская математическая рукопись, хранящаяся в Британском музее в Лондоне; названа по имени её составителя писца Ахмеса (около 2000 до н. э.). См. Папирусы математические … Большая советская энциклопедия
Ахмеса папирус — папирус Ринда др. егип. математич. рукопись … Древний мир. Энциклопедический словарь