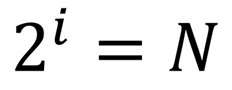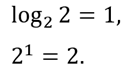В чем состоит суть содержательного подхода к определению количества
Измерение информации. Содержательный подход
Урок 5. Информатика 10 класс (ФГОС)
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Измерение информации. Содержательный подход»
· содержательный подход к измерению информации;
· неопределённость знания об исходе некоторого события;
· единица измерения количества информации в рамках содержательного подхода.
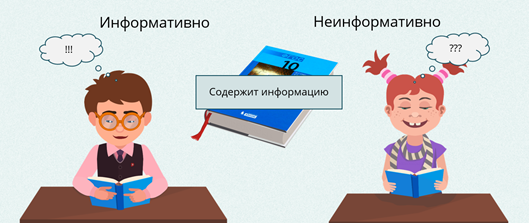
Количество информации в одном том же сообщении, с точки зрения разных людей, может быть разным. Например, для человека, который не владеет английским языком, статья, напечатанная на английском языке, не несёт никакой информации. Информативным для человека является то сообщение, которое содержит новые и понятные сведения.
Давайте попробуем определить количество информации с позиции «информативно» или «неинформативно» для ученика 10 класса.
Столица России – Москва (это сообщение неинформативно, так как всем известно).
Высота Останкинской телебашни составляет 540 метров (или 45 этажей). Это делает её 6 по высоте конструкцией в мире (это сообщение информативно).
Корреляция, корреляционная зависимость — это зависимость между величинами, каждая из которых подвергается неконтролируемому разбросу (неинформативно, так как непонятно).
Необходимо отличать понятия информация и информативность.
Например, содержит ли учебник по информатике для десятого класса информацию? Конечно содержит, но для кого он будет информативным – для ученика десятого класса или первого класса? Естественно для ученика десятого класса. Первоклассник ничего из этого учебника не поймёт.
Теперь мы можем сделать вывод: количество информации зависит от информативности.
Информативность можно обозначить единицей, неинформативная информация равна нулю. Но это не даёт точного определения количества информации.
Алфавитный подход применяется для измерения информации, используемой компьютером. Так как компьютер не понимает смысла информации.
Содержательный подход применяется для измерения информации, используемой человеком.
В содержательном подходе, количество информации, заключённое в сообщении, определяется объёмом знаний, который это сообщение несёт получающему его человеку.
Тогда сущность содержательного подхода заключается в следующем: количество информации, заключённое в сообщении, должно быть тем больше, чем больше оно пополняет наши знания.
То есть, чем больше первоначальная неопределённость знания, тем больше информации несёт сообщение, снимающее эту неопределённость.
Допустим, вы бросаете монету, загадывая, что выпадет: орёл или решка. Есть всего два возможных результата бросания монеты.
Причём ни один из этих результатов не имеет преимущества перед другим. В таком случае говорят, что они равновероятны.
В данном случае с монетой, перед её подбрасыванием неопределённость знания о результате равна 2.
Если же бросать игральный кубик с шестью гранями, то он может с равной вероятностью упасть на любую из них. Значит, неопределённость знания о результате бросания кубика равна 6.
Или такая ситуация: спортсмены-бегуны перед забегом путём жеребьёвки определяют свои порядковые номера на старте. Допустим, что в забеге участвует 100 спортсменов, тогда неопределённость знания спортсмена о своём номере до жеребьёвки равна 100.
Вернёмся к спортсменам-бегунам.
Здесь событие – это жеребьёвка спортсменов; исход – спортсмену выпал, например, номер 34.
Итак, в первом примере возможны два варианта ответа: орёл, решка; во втором примере шесть вариантов: 1, 2, 3, 4, 5, 6.
В третьем примере – 100 вариантов, может выпасть номер от 1 до 100.
Теперь, согласно определению, можно сделать вывод, что наибольшее количество информации несёт третье сообщение, так как неопределённость знания об исходе события в этом случае была наибольшей.
В 40-х годах 20 века Клод Шеннон — американский учёный и инженер, один из создателей математической теории информации, решил проблему измерения информации.
Шеннон дал такое определение информации: Информация – это снятая неопределённость знания человека об исходе какого-то события.
Вернёмся к примеру, с монетой. После того как вы бросили монету и посмотрели на неё, вы получили зрительное сообщение, что выпал, например, орёл. Определился один из двух возможных результатов. Неопределённость знания уменьшилась в два раза: было два варианта, остался один. Значит, узнав результат бросания монеты, вы получили 1 бит информации.
Сообщение об одном из двух равновероятных результатов некоторого события несёт 1 бит информации.
А также сообщение, уменьшающее неопределённость знания об исходе некоторого события в два раза, несёт 1 бит информации.
Или такой пример. Вы подошли к светофору на пешеходном переходе, когда горел красный свет. Загорелся зелёный. Здесь вы также получили один бит информации.
Итак, мы выяснили, когда сообщение несёт 1 бит информации.
Значит в примерах с кубиком и спортсменами количество информации будет больше. Давайте выясним как измерить это количество.
Рассмотрим пример. Занятия могут состояться в одном из кабинетов, номера которых от одного до шестнадцати. Ученики спросили у учителя: «в каком кабинете будут проходить занятия?» На что учитель им ответил: «Угадайте ответ за четыре вопроса, на которые я могу дать ответ «Да» или «Нет»».
Подумав староста класса задала следующие вопросы:
1 вопрос. Номер кабинета меньше 9? – Да. Ответил учитель
2 вопрос. Номер кабинета больше 4? – Да.
3 вопрос. Номер кабинета чётный? – Нет.
4 вопрос. Номер кабинета 5? – Нет.
Ученики поняли, что занятия состоятся в кабинете номер 7.
Итак, сколько же информации получили ученики?
Первоначально неопределённость знания (количество возможных кабинетов) была равна 16. С ответом на каждый вопрос неопределённость знания уменьшалась в два раза и, следовательно, согласно данному выше определению, передавался 1 бит информации.
Первоначально было 16 вариантов. После первого вопроса осталось 8 вариантов, и ученики получили 1 бит информации.
После 2 вопроса осталось 4 варианта, и ученики получили ещё 1 бит информации.
После 3 вопроса осталось 2 варианта и был получен ещё 1 бит информации.
И, наконец после 4 вопроса, остался 1 вариант и получен ещё 1 бит информации.
То есть мы можем сделать вывод, что ученики получили четыре бит информации.
Такой способ нахождения количества информации, называется методом половинного деления: здесь ответ на каждый заданный вопрос уменьшает неопределённость знания, которая имеется до ответа на этот вопрос, наполовину. Каждый такой ответ несёт 1 бит информации.
Нужно отметить, что методом половинного деления наиболее удобно решать подобные проблемы. Таким способом всегда можно угадать, например, любой из 32 вариантов максимум за 5 вопросов.
Если бы поиск совершался последовательным перебором: «Мы будем заниматься в первом кабинете?» «Нет», «Во втором кабинете?» «Нет» и т. д., то про седьмой кабинет можно было бы узнать после семи вопросов, а про восьмой — после восьми.
Теперь мы можем полученные результаты описать с помощью следующих определений:
• сообщение об одном из двух равновероятных исходов некоторого события несёт 1 бит информации;
• сообщение об одном из четырёх равновероятных исходов некоторого события несёт 2 бита информации;
• сообщение об одном из восьми равновероятных исходов некоторого события несёт 3 бита информации.
Для того чтобы при измерении одной и той же информации получалось одно и то же значение количества информации, необходимо договориться об использовании определённого алфавита.
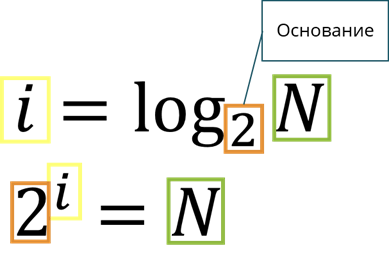
Пусть N – это количество возможных исходов события или неопределённость знания. Тогда i – это количество информации в сообщении об одном из N результатов.
Вернёмся к нашим примерам.
Обратите внимание, между данными величинами есть связь, которая выражается формулой.
Эта формула вам уже знакома. Также вы с ней встретитесь ещё не раз. Эта формула очень важна, поэтому её называют главной формулой информатики.
Для определения количества информации I, содержащейся в сообщении о том, что произошло одно из N равновероятных событий, нужно решить уравнение.
В математике такое уравнение называется показательным.
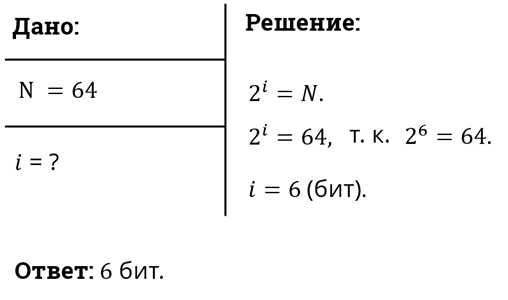
Рассмотрим пример. В коробке лежало 64 разноцветных катушки ниток. Сколько информации несёт сообщение о том, что из коробки достали жёлтую катушку?
Рассмотрим следующий пример.
В скором поезде Москва – Санкт-Петербург 8 вагонов, в каждом вагоне 32 места. Нужно определить какое количество информации несёт сообщение о том, что вам купили билет в 6 вагон, 13 место?
Этот пример показывает выполнение закона аддитивности количества информации (правило сложения): количество информации в сообщении одновременно о нескольких результатах независимых друг от друга событий равно сумме количеств информации о каждом событии отдельно.
Итак, мы уже говорили о том, что с формулой 2 i = N мы уже встречались на прошлом уроке, когда говорили об алфавитном подходе к измерению информации. Тогда N рассматривалось как мощность алфавита, a i — как информационный вес каждого символа алфавита.
Если допустить, что все символы алфавита появляются в тексте с одинаковой частотой, то есть равновероятно, то информационный вес символа i идентичен количеству информации в сообщении о появлении любого символа в тексте. При этом N — неопределённость знания о том, какой именно символ алфавита должен стоять в данной позиции текста. Это замечание показывает связь между алфавитным и содержательным подходами к измерению информации.
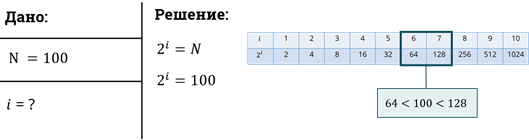
Рассмотрим пример: Требуется угадать задуманное число из диапазона целых чисел, например, от 1 до 100. Чему равно количество информации в сообщении о том, что загаданное число 89?
То есть, если значение N равно целой степени двойки, то показательное уравнение легко решить, а если нет, как в нашем примере. Как поступить в этом случае?
Можно догадаться, что решением уравнения будет дробное число, которое находится между 6 и 7.
В математике существует функция, с помощью которой решаются показательные уравнения. Эта функция называется логарифмом.
Тогда решение показательного уравнения запишется i равно логарифм N по основанию 2. Это означает, что мы должны найти степень, в которую нужно возвести основание, в нашем случае 2, чтобы получить N.
Например, для целых степеней двойки получим:
Значения логарифмов находятся с помощью специальных логарифмических таблиц. Также можно использовать инженерный калькулятор или табличный процессор.
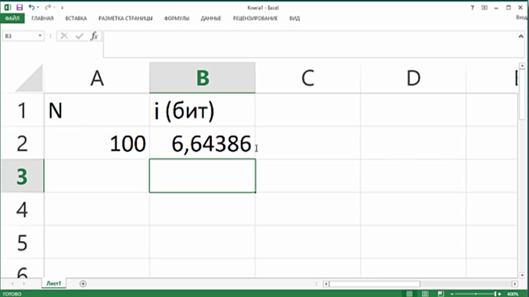
Определим количество информации, полученной из сообщения об угадывании задуманного числа из диапазона от одного до ста, с помощью электронной таблицы.
Количество информации в сообщении о том, что загаданное число 89 приблизительно равно 6,64 бит.
Формула для измерения количества информации была предложена американским учёным-электронщиком Ральфом Хартли, который является одним из основоположников теории информации.
Данный пример показал, что количество информации, определяемое с использованием содержательного подхода, может быть дробной величиной, если же находить информационный объем, путём применения алфавитного подхода, то там может быть только целочисленное значение.
В содержательном подходе количество информации, заключённое в сообщении, определяется объёмом знаний, который это сообщение несёт получающему его человеку.
Сообщение, уменьшающее неопределённость знания в два раза, несёт один бит информации.
Для измерения количества информации применяется формула Хартли:
В чем состоит суть содержательного подхода к определению количества
Вопрос: «Как измерить информацию?» очень непростой. Ответ на него зависит от того, что понимать под информацией. Но поскольку определять информацию можно по-разному, то и способы измерения тоже могут быть разными.
Содержательный подход к измерению информации.
Для человека информация — это знания человека. Рассмотрим вопрос с этой точки зрения.
Получение новой информации приводит к расширению знаний. Если некоторое сообщение приводит к уменьшению неопределенности нашего знания, то можно говорить, что такое сообщение содержит информацию.
Отсюда следует вывод, что сообщение информативно (т.е. содержит ненулевую информацию), если оно пополняет знания человека. Например, прогноз погоды на завтра — информативное сообщение, а сообщение о вчерашней погоде неинформативно, т.к. нам это уже известно.
Нетрудно понять, что информативность одного и того же сообщения может быть разной для разных людей. Например: «2×2=4» информативно для первоклассника, изучающего таблицу умножения, и неинформативно для старшеклассника.
Но для того чтобы сообщение было информативно оно должно еще быть понятно. Быть понятным, значит быть логически связанным с предыдущими знаниями человека. Определение «значение определенного интеграла равно разности значений первообразной подынтегральной функции на верхнем и на нижнем пределах», скорее всего, не пополнит знания и старшеклассника, т.к. оно ему не понятно. Для того, чтобы понять данное определение, нужно закончить изучение элементарной математики и знать начала высшей.
Получение всяких знаний должно идти от простого к сложному. И тогда каждое новое сообщение будет в то же время понятным, а значит, будет нести информацию для человека.
Сообщение несет информацию для человека, если содержащиеся в нем сведения являются для него новыми и понятными.
Очевидно, различать лишь две ситуации: «нет информации» — «есть информация» для измерения информации недостаточно. Нужна единица измерения, тогда мы сможем определять, в каком сообщении информации больше, в каком — меньше.
Единица измерения информации была определена в науке, которая называется теорией информации. Эта единица носит название «бит». Ее определение звучит так:
Например, после сдачи зачета или выполнения контрольной работы ученик мучается неопределенностью, он не знает, какую оценку получил. Наконец, учитель объявляет результаты, и он получаете одно из двух информационных сообщений: «зачет» или «незачет», а после контрольной работы одно из четырех информационных сообщений: «2», «3», «4» или «5».
Информационное сообщение об оценке за зачет приводит к уменьшению неопределенности знания в два раза, так как получено одно из двух возможных информационных сообщений. Информационное сообщение об оценке за контрольную работу приводит к уменьшению неопределенности знания в четыре раза, так как получено одно из четырех возможных информационных сообщений.
Рассмотрим еще один пример.
На книжном стеллаже восемь полок. Книга может быть поставлена на любую из них. Сколько информации содержит сообщение о том, где находится книга?
Применим метод половинного деления. Зададим несколько вопросов уменьшающих неопределенность знаний в два раза.
Каждый ответ уменьшал неопределенность в два раза.
Всего было задано три вопроса. Значит набрано 3 бита информации. И если бы сразу было сказано, что книга лежит на первой полке, то этим сообщением были бы переданы те же 3 бита информации.
Если обозначить возможное количество событий, или, другими словами, неопределенность знаний N, а буквой I количество информации в сообщении о том, что произошло одно из N событий, то можно записать формулу:
Количество информации, содержащееся в сообщении о том, что произошло одно из N равновероятных событий, определяется из решения показательного уравнения: 2 I = N.
Пример: Вы бросаете монету, загадывая, что выпадет: орел или решка?
Решение: Есть два варианта возможного результата бросания монеты. Ни один из этих вариантов не имеет преимущества перед другим (равновероятны). Перед подбрасыванием монеты неопределенность знаний о результате равна двум.
После совершения действия неопределенность уменьшилась в 2 раза. Получили 1 бит информации.
Ответ: Результат подбрасывания монеты принес 1 бит информации.
Учитель информатики
Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.
Подходы к измерению информации
§ 2. Подходы к измерению информации
Информатика. 10 класса. Босова Л.Л. Оглавление
Информация и её свойства
Информация и её свойства являются объектом исследования целого ряда научных дисциплин, таких как:
♦ теория информации (математическая теория систем передачи информации);
♦ кибернетика (наука об общих закономерностях процессов управления и передачи информации в машинах, живых организмах и обществе);
♦ информатика (изучение процессов сбора, преобразования, хранения, защиты, поиска и передачи всех видов информации и средств их автоматизированной обработки);
♦ семиотика (наука о знаках и знаковых системах);
♦ теория массовой коммуникации (исследование средств массовой информации и их влияния на общество) и др.
Рассмотрим более детально подходы к определению понятия информации, важные с позиций её измерения:
1) определение К. Шеннона, применяемое в математической теории информации;
2) определение А. Н. Колмогорова, применяемое в отраслях информатики, связанных с использованием компьютеров.
2.1. Содержательный подход к измерению информации
Клод Шеннон, разрабатывая теорию связи, предложил характеризовать информативность сообщения содержащейся в нём полезной информацией, т. е. той частью сообщения, которая снимает полностью или уменьшает существующую до её получения неопределённость какой-либо ситуации.
Клод Элвуд Шеннон (1916-2001) — американский инженер и математик. Является основателем теории информации, нашедшей применение в современных высокотехнологических системах связи. В 1948 году предложил использовать слово «бит» для обозначения наименьшей единицы информации.
Информация — это снятая неопределённость. Величина неопределённости некоторого события — это количество возможных результатов (исходов) данного события.
Сообщение, уменьшающее неопределённость знания в 2 раза, несёт 1 бит информации.
Такой подход к измерению информации называют содержательным.
Пример 1. Допустим, вы подбрасываете монету, загадывая, что выпадет: «орёл» или «решка». Перед подбрасыванием монеты неопределённость знания о результате равна двум. Действительно, есть всего два возможных результата этого события (бросания монеты). Эти результаты мы считаем равновероятными, т. к. ни один из них не имеет преимущества перед другим.
После того как конкретный исход стал известен (например, подброшенная монета упала «орлом» вверх), неопределённость уменьшилась в 2 раза. Таким образом, сообщение о том, что подброшенная монета упала «орлом» вверх, несёт в себе 1 бит информации.
Пример 2. Предположим, в книжном шкафу восемь полок. Книга может быть поставлена на любую из них. Сколько бит информации несёт сообщение о том, что книга поставлена на третью полку?
Ответ на этот вопрос можно получить, если дополнить исходное сообщение ещё несколькими сообщениями так, чтобы каждое из них уменьшало неопределённость знания в 2 раза.
Итак, количество возможных результатов (исходов) события, состоящего в том, что книга поставлена в шкаф, равно восьми: 1, 2, 3, 4, 5, 6, 7 и 8.
Сообщение «Книга поставлена на полку не выше четвёртой» уменьшает неопределённость знания о результате в два раза. Действительно, после такого сообщения остаётся всего четыре варианта: 1, 2, 3 и 4. Получен один бит информации.
Сообщение «Книга поставлена на полку выше второй» уменьшает неопределённость знания о результате в два раза: после этого сообщения остаётся всего два варианта: 3 и 4. Получен ещё один (второй) бит информации.
Сообщение «Книга поставлена на третью полку» также уменьшает неопределённость знания о результате в два раза. Получен третий бит информации.
Итак, мы построили цепочку сообщений, каждое из которых уменьшало неопределённость знания о результате в два раза, т. е. несло 1 бит информации. Всего было набрано 3 бита информации. Именно столько информации и содержится в сообщении «Книга поставлена на третью полку».
Подумайте, сколько информации содержится в сообщении о том, что книга поставлена на пятую полку. Обоснуйте свой ответ, построив соответствующую цепочку сообщений.
Метод поиска, на каждом шаге которого отбрасывается половина вариантов, называется методом половинного деления. Этот метод широко используется в компьютерных науках.
Пример 3. О результатах футбольного матча между клубами «Спартак» и «Динамо» известно, что больше трёх мячей никто не забил. Всего возможных вариантов счёта матча — 16:
Здесь первая цифра в каждой паре соответствует количеству мячей, забитых командой «Спартак», вторая — командой «Динамо».
Будем считать все варианты равновероятными и отгадывать счёт, задавая вопросы, на которые можно ответить только «да» или «нет». Вопросы будем формулировать так, чтобы количество возможных вариантов счёта каждый раз уменьшалось вдвое. Это позволит нам:
1) обойтись минимальным количеством вопросов;
2) подсчитать, сколько бит информации содержит сообщение о счёте матча.
Вопрос 1. «Спартак» забил больше одного мяча? Предположим, получен ответ «Нет». Такой ответ позволяет не рассматривать варианты, расположенные в нижней части таблицы, т. е. сокращает количество возможных исходов в 2 раза:
Вопрос 2. «Спартак» забил один мяч? Предположим, получен ответ «Да». Такой ответ позволяет не рассматривать варианты, расположенные в верхней строке таблицы, т. е. сокращает количество возможных исходов ещё в 2 раза:
Вопрос 3. «Спартак» пропустил больше одного мяча? Предположим, получен ответ «Нет». Можно отбросить ещё два варианта:
Вопрос 4. «Спартак» пропустил один мяч? Предположим, получен ответ «Да». Получаем единственный вариант:
Итак, нам удалось выяснить счёт матча, задав четыре вопроса, ответ на каждый из которых уменьшал неопределённость результата в два раза, т. е. нёс 1 бит информации. Сообщение о счёте матча несёт четыре бита информации.
Выясните, какому счёту матча будут соответствовать следующие цепочки ответов на поставленные выше вопросы:
2) Нет — Нет — Нет — Нет;
3) Да — Нет — Да — Нет.
Попробуйте придумать такие вопросы, чтобы цепочка ответов Нет — Да — Нет — Да приводила к счёту 2 : 3.
Вычислять количество информации, содержащееся в сообщении о том, что имел место один из множества равновероятных результатов некоторого события, с помощью метода половинного деления возможно, но затруднительно. Гораздо проще воспользоваться следующей закономерностью.
Количество информации i, содержащееся в сообщении об одном из N равновероятных результатов некоторого события, определяется из формулы: 2 i = N.
При N, равном целой степени двойки (2, 4, 8, 16, 32 и т. д.), это уравнение легко решается в уме. Решать такие уравнения при других N вы научитесь чуть позже, в курсе математики 11 класса.
Примюр 4. Петя и Вася заинтересовались игрой «Крестики — нолики» на поле n х n. Количество информации, полученное вторым игроком после первого хода первого игрока, составляет б бит. Требуется выяснить размеры поля, на котором играют Петя и Вася.
2.2. Алфавитный подход к измерению информации
Определение количества информации на основе уменьшения неопределённости наших знаний рассматривает информацию с точки зрения её содержания, понятности и новизны для человека. С этой точки зрения в примере о подбрасывании монеты одинаковое количество информации содержит и зрительный образ упавшей монеты, и короткое сообщение «Орёл», и длинная фраза «В результате подбрасывания монета упала так, что на её видимой части изображён орёл».
Однако при хранении и передаче информации с помощью технических устройств целесообразно отвлечься от её содержания и рассматривать информацию как последовательность символов (букв, цифр, кодов цвета точек изображения и т. д.) некоторого алфавита.
Информация — последовательность символов (букв, цифр, кодов цвета точек изображения и т. д.) некоторого алфавита.
Минимальная мощность алфавита (количество входящих в него символов), пригодного для кодирования информации, равна 2. Такой алфавит называется двоичным. Один символ двоичного алфавита несёт 1 бит информации.
Согласно Колмогорову, количество информации, содержащейся в последовательности символов, определяется минимально возможным количеством двоичных знаков, необходимых для кодирования этой последовательности, безотносительно к содержанию представленного ею сообщения. Данный подход к определению количества информации называют алфавитным.
Андрей Николаевич Колмогоров (1903-1987) — один из крупнейших математиков XX века. Им получены основополагающие результаты в математической логике, теории сложности алгоритмов, теории информации, теории множеств и ряде других областей математики и её приложений.
Информационным объёмом сообщения называется количество двоичных символов, которое используется для кодирования этого сообщения. В двоичном коде один двоичный разряд несёт 1 бит информации.
В отличие от определения количества информации по Колмогорову в определении информационного объёма не требуется, чтобы число двоичных символов было минимально возможным. При оптимальном кодировании понятия количества информации и информационного объёма совпадают.
Из курса информатики основной школы вы знаете, что двоичные коды бывают равномерные и неравномерные. Равномерные коды в кодовых комбинациях содержат одинаковое число символов, неравномерные — разное.
Первый равномерный двоичный код был изобретён французом Жаном Морисом Бодо в 1870 году. В коде Бодо используются сигналы двух видов, имеющие одинаковую длительность и абсолютную величину, но разную полярность. Длина кодов всех символов алфавита равна пяти (рис. 1.7).
Рис. 1.7. Фрагмент кодовой таблицы кода Бодо
Всего с помощью кода Бодо можно составить 2 5 = 32 комбинации.
Пример 5. Слово WORD, закодированное с помощью кода Бодо, будет выглядеть так:
Информационный объём такого сообщения равен 20 битам; таково количество двоичных символов, которое используется для кодирования этого сообщения.
Пример 6. Для двоичного представления текстов в компьютере чаще всего используется равномерный восьмиразрядный код. С его помощью можно закодировать алфавит из 256 символов (2 8 = 256). Фрагмент кодовой таблицы ASCII представлен на рисунке 1.8.
Рис. 1.8. Фрагмент кодовой таблицы ASCII
Слово WORD, закодированное с помощью таблицы ASCII:
Информационный объём такого сообщения равен 32 битам.
Из курса информатики основной школы вам известно, что с помощью i-разрядного двоичного кода можно закодировать алфавит, мощность N которого определяется из соотношения:
2 i = N.
Иными словами, зная мощность используемого алфавита, всегда можно вычислить информационный вес символа — минимально возможное количество бит, требуемое для кодирования символов этого алфавита. При этом информационный вес символа должен быть выражен целым числом.
Соотношение для определения информационного веса символа алфавита можно получить и из следующих соображений.
Пусть N — мощность алфавита, используемого для кодирования сообщений. При этом в каждом конкретном сообщении какие-то символы алфавита будут использоваться чаще, какие-то — реже, а какие-то — не будут использоваться вообще. Не станем обращать на это внимание, наоборот, будем считать, что любой из символов может появиться в сообщении с равной вероятностью. Другими словами, появление в сообщении очередного символа — одно из N равновероятных событий. Но количество информации i, содержащееся в сообщении об одном из N равновероятных результатов некоторого события, определяется из формулы 2 i = N.
Алгоритм вычисления информационного объёма сообщения выглядит так:
1) определить мощность используемого алфавита N;
2) из соотношения 2 i = N определить i — информационный вес символа алфавита в битах (длину двоичного кода символа из используемого алфавита мощности N);
3) вычислить информационный объём сообщения I, умножив информационный вес символа i на количество символов в сообщении К.
При алфавитном подходе информационный объём сообщения I, состоящего из К символов, вычисляется по формуле:
I = К * i,
где I — информационный вес символа в битах, связанный с мощностью используемого алфавита N соотношением:
2 i = N.
Пример 7. Для регистрации на некотором сайте пользователю надо придумать пароль, состоящий из 10 символов. В качестве символов можно использовать десятичные цифры и шесть первых букв латинского алфавита, причём буквы используются только заглавные. Пароли кодируются посимвольно. Все символы кодируются одинаковым и минимально возможным количеством бит. Для хранения сведений о каждом пользователе в системе отведено одинаковое и минимально возможное целое число байт.
Необходимо выяснить, какой объём памяти потребуется для хранения 100 паролей.
2.3. Единицы измерения информации
Итак, в двоичном коде один двоичный разряд несёт 1 бит информации. 8 бит образуют один байт. Помимо бита и байта, для измерения информации используются более крупные единицы:
1 Кбайт (килобайт) = 2 10 байт;
1 Мбайт (мегабайт) = 2 10 Кбайт = 2 20 байт;
1 Гбайт (гигабайт) = 2 10 Мбайт = 2 20 Кбайт = 2 30 байт;
1 Тбайт (терабайт) = 2 10 Гбайт = 2 20 Мбайт = 2 30 Кбайт = 2 40 байт;
1 Пбайт (петабайт) = 2 10 Тбайт = 2 20 Гбайт = 2 30 Мбайт = 2 40 Кбайт = 2 50 байт.
Чтобы избежать путаницы с различным использованием одних и тех же приставок, в 1999 г. Международная электротехническая комиссия ввела новый стандарт наименования двоичных приставок. Согласно этому стандарту, 1 килобайт равняется 1000 байт, а величина 1024 байта получила новое название — 1 кибибайт (Кибайт).
У нас в стране в 2009 году принято «Положение о единицах величин, допускаемых к применению в Российской Федерации». В нём сказано, что наименование и обозначение единицы количества информации «байт» (1 байт = 8 бит) применяются с двоичными приставками «кило», «мега», «гига», которые соответствуют множителям «2 10 », «2 20 » и «2 30 » (1 Кбайт = 1024 байт, 1 Мбайт = 1024 Кбайт, 1 Гбайт = 1024 Мбайт). Данные приставки пишутся с большой буквы.
Рассмотрим ещё несколько примеров решения задач, связанных с определением информационного объёма сообщений.
Пример 8. При регистрации в компьютерной системе каждому пользователю выдаётся пароль длиной в 12 символов, образованный из десятичных цифр и первых шести букв английского алфавита, причём буквы могут использоваться как строчные, так и прописные — соответствующие символы считаются разными. Пароли кодируются посимвольно. Все символы кодируются одинаковым и минимально возможным количеством бит. Для хранения сведений о каждом пользователе в системе отведено одинаковое и минимально возможное целое число байт.
Кроме собственно пароля для каждого пользователя в системе хранятся дополнительные сведения, для которых отведено 12 байт. На какое максимальное количество пользователей рассчитана система, если для хранения сведений о пользователях в ней отведено 200 Кбайт?
Прежде всего, выясним мощность алфавита, используемого для записи паролей: N — 6 (буквы прописные) + 6 (буквы строчные) + 10 (десятичные цифры) = 22 символа.
Для кодирования одного из 22 символов требуется 5 бит памяти (4 бита позволят закодировать всего 2 4 = 16 символов, 5 бит позволят закодировать уже 2 5 = 32 символа); 5 — минимально возможное количество бит для кодирования 22 разных символов алфавита, используемого для записи паролей.
Для хранения всех 12 символов пароля требуется 12 • 5 = 60 бит. Из условия следует, что пароль должен занимать целое число байт; т. к. 60 не кратно восьми, возьмём ближайшее большее значение, которое кратно восьми: 64 = 8 • 8. Таким образом, один пароль занимает 8 байт.
Информация о пользователе занимает 20 байт, т. к. содержит не только пароль (8 байт), но и дополнительные сведения (12 байт).
Максимальное количество пользователей («польз.»), информацию о которых можно сохранить в системе, равно 10 240:
Пример 9. Объём сообщения, состоящего из 8192 символов, равен 16 Кбайт. Какова максимальная мощность алфавита, использованного при передаче сообщения?
САМОЕ ГЛАВНОЕ
Информация (по Шеннону) — это снятая неопределённость. Величина неопределённости некоторого события — это количество возможных результатов (исходов) данного события. Сообщение, уменьшающее неопределённость знания в 2 раза, несёт 1 бит информации. Количество информации i, содержащееся в сообщении об одном из N равновероятных результатов некоторого события, определяется из формулы: 2 i = N. Такой подход к измерению информации называют содержательным.
Информация (по Колмогорову) — последовательность символов (букв, цифр, кодов цвета точек изображения и т. д.) некоторого алфавита. Информационным объёмом сообщения называется количество двоичных символов, которое используется для кодирования этого сообщения. В двоичном коде один двоичный разряд несёт 1 бит информации. Такой подход к измерению информации называют алфавитным.
При алфавитном подходе информационный объём сообщения I, состоящего из К символов, вычисляется по формуле:
I = K * i, где i — информационный вес символа в битах, связанный с мощностью используемого алфавита N соотношением 2 i = N. Единицы измерения информации:
1 Кбайт (килобайт) = 2 10 байт;
1 Мбайт (мегабайт) = 2 10 Кбайт = 2 20 байт;
1 Гбайт (гигабайт) = 2 10 Мбайт = 2 20 Кбайт = 2 30 байт;
1 Тбайт (терабайт) = 2 10 Гбайт = 2 20 Мбайт = 2 30 Кбайт = 2 40 байт;
1 Пбайт (петабайт) = 2 10 Тбайт = 2 20 Гбайт = 2 30 Мбайт = 2 40 Кбайт = 2 50 байт.
Вопросы и задания
1. Что такое неопределённость знания о результате какого-либо события? Приведите пример.
2. В чём состоит суть содержательного подхода к определению количества информации? Что такое бит с точки зрения содержательного подхода?
3. Паролем для приложения служит трёхзначное число в шестнадцатеричной системе счисления. Возможные варианты пароля:
Ответ на какой вопрос (см. ниже) содержит 1 бит информации?
1) Это число записано в двоичной системе счисления?
2) Это число записано в четверичной системе счисления?
3) Это число может быть записано в восьмеричной системе счисления?
4) Это число может быть записано в десятичной системе счисления?
5) Это число может быть записано в шестнадцатеричной системе счисления?
4. При угадывании целого числа в некотором диапазоне было получено 5 бит информации. Каковы наибольшее и наименьшее числа этого диапазона?
5. Какое максимальное количество вопросов достаточно задать вашему собеседнику, чтобы точно определить день и месяц его рождения?
6. В чём состоит суть алфавитного подхода к измерению информации? Что такое бит с точки зрения алфавитного подхода?
7. Закодируйте фразу «ALL IN GOOD TIME» кодом Бодо и восьмиразрядным компьютерным кодом. Сравните полученные информационные объёмы текста.
8. Какие единицы используются для измерения объёма информации, хранящейся на компьютере?
9. Объём сообщения, содержащего 11 264 символа, равен 11 Кбайт. Определите максимальную мощность алфавита, который мог быть использован для кодирования этого сообщения? Какова минимальная мощность алфавита, использование которого привело к такому же информационному объёму закодированного сообщения?
10. В школе 750 учащихся, коды учащихся записаны в школьной информационной системе с помощью минимального количества бит. Каков информационный объём в байтах сообщения о кодах 180 учащихся начальных классов?
11. В школьной базе данных каждый ученик получил идентификатор, состоящий ровно из б символов. В качестве символов используются все заглавные буквы русского алфавита, кроме «Ё», «Ы», «Ъ» и «Ь», а также все десятичные цифры за исключением цифры 0. Каждый такой идентификатор в информационной системе записывается минимально возможным и одинаковым целым количеством байт (при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством бит). Определите объём памяти, необходимый для хранения в этой системе 180 идентификаторов учащихся начальных классов. Ответ выразите в килобайтах.
12. В ходе телевизионного шоу проводится СМС-голосование: каждый телезритель отдаёт свой голос за одного из 12 артистов-участников шоу, отправляя сообщение с его номером. Голос каждого телезрителя, отданный за того или иного участника, кодируется одинаковым и минимально возможным количеством бит и сохраняется для подведения итогов. За время телевизионного шоу в голосовании приняли участие 163 840 зрителей. Определите объём сохранённой информации о голосовании и выразите его в килобайтах.
13. При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 6 символов и содержащий только символы из шестибуквенного набора А, В, С, D, Е, F. Для хранения сведений о каждом пользователе отведено одинаковое и минимально возможное целое число байт. При этом используют посимвольное кодирование паролей и все символы кодируются одинаковым и минимально возможным количеством бит. Кроме собственно пароля для каждого пользователя в системе хранятся дополнительные сведения, занимающие 15 байт. Определите объём памяти в байтах, необходимый для хранения сведений о 120 пользователях.