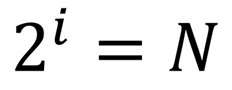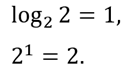В чем суть содержательного подхода к измерению информации
В чем суть содержательного подхода к измерению информации
Вопрос: «Как измерить информацию?» очень непростой. Ответ на него зависит от того, что понимать под информацией. Но поскольку определять информацию можно по-разному, то и способы измерения тоже могут быть разными.
Содержательный подход к измерению информации.
Для человека информация — это знания человека. Рассмотрим вопрос с этой точки зрения.
Получение новой информации приводит к расширению знаний. Если некоторое сообщение приводит к уменьшению неопределенности нашего знания, то можно говорить, что такое сообщение содержит информацию.
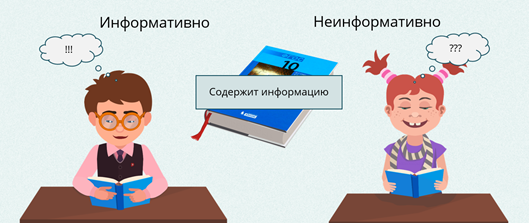
Отсюда следует вывод, что сообщение информативно (т.е. содержит ненулевую информацию), если оно пополняет знания человека. Например, прогноз погоды на завтра — информативное сообщение, а сообщение о вчерашней погоде неинформативно, т.к. нам это уже известно.
Нетрудно понять, что информативность одного и того же сообщения может быть разной для разных людей. Например: «2×2=4» информативно для первоклассника, изучающего таблицу умножения, и неинформативно для старшеклассника.
Но для того чтобы сообщение было информативно оно должно еще быть понятно. Быть понятным, значит быть логически связанным с предыдущими знаниями человека. Определение «значение определенного интеграла равно разности значений первообразной подынтегральной функции на верхнем и на нижнем пределах», скорее всего, не пополнит знания и старшеклассника, т.к. оно ему не понятно. Для того, чтобы понять данное определение, нужно закончить изучение элементарной математики и знать начала высшей.
Получение всяких знаний должно идти от простого к сложному. И тогда каждое новое сообщение будет в то же время понятным, а значит, будет нести информацию для человека.
Сообщение несет информацию для человека, если содержащиеся в нем сведения являются для него новыми и понятными.
Очевидно, различать лишь две ситуации: «нет информации» — «есть информация» для измерения информации недостаточно. Нужна единица измерения, тогда мы сможем определять, в каком сообщении информации больше, в каком — меньше.
Единица измерения информации была определена в науке, которая называется теорией информации. Эта единица носит название «бит». Ее определение звучит так:
Например, после сдачи зачета или выполнения контрольной работы ученик мучается неопределенностью, он не знает, какую оценку получил. Наконец, учитель объявляет результаты, и он получаете одно из двух информационных сообщений: «зачет» или «незачет», а после контрольной работы одно из четырех информационных сообщений: «2», «3», «4» или «5».
Информационное сообщение об оценке за зачет приводит к уменьшению неопределенности знания в два раза, так как получено одно из двух возможных информационных сообщений. Информационное сообщение об оценке за контрольную работу приводит к уменьшению неопределенности знания в четыре раза, так как получено одно из четырех возможных информационных сообщений.
Рассмотрим еще один пример.
На книжном стеллаже восемь полок. Книга может быть поставлена на любую из них. Сколько информации содержит сообщение о том, где находится книга?
Применим метод половинного деления. Зададим несколько вопросов уменьшающих неопределенность знаний в два раза.
Каждый ответ уменьшал неопределенность в два раза.
Всего было задано три вопроса. Значит набрано 3 бита информации. И если бы сразу было сказано, что книга лежит на первой полке, то этим сообщением были бы переданы те же 3 бита информации.
Если обозначить возможное количество событий, или, другими словами, неопределенность знаний N, а буквой I количество информации в сообщении о том, что произошло одно из N событий, то можно записать формулу:
Количество информации, содержащееся в сообщении о том, что произошло одно из N равновероятных событий, определяется из решения показательного уравнения: 2 I = N.
Пример: Вы бросаете монету, загадывая, что выпадет: орел или решка?
Решение: Есть два варианта возможного результата бросания монеты. Ни один из этих вариантов не имеет преимущества перед другим (равновероятны). Перед подбрасыванием монеты неопределенность знаний о результате равна двум.
После совершения действия неопределенность уменьшилась в 2 раза. Получили 1 бит информации.
Ответ: Результат подбрасывания монеты принес 1 бит информации.
Информатика. 10 класс
Конспект урока
Информатика, 10 класс. Урок № 2.
Тема — Подходы к измерению информации
Перечень вопросов, рассматриваемых в теме: Информация как снятая неопределенность. Содержательный подход к измерению информации.
Информация как последовательность символов некоторого алфавита. Алфавитный подход к измерению информации. Единицы измерения информации. Понятие больших данных
Глоссарий по теме: Информатика, информация, свойства информации (объективность, достоверность, полнота, актуальность, понятность, релевантность), виды информации, информационные процессы, информационная культура, информационная грамотность.
Основная литература по теме урока:
Л. Л. Босова, А. Ю. Босова. Информатика. Базовый уровень: учебник для 10 класса — М.: БИНОМ. Лаборатория знаний, 2017
Дополнительная литература по теме урока:
И. Г. Семакин, Т. Ю. Шеина, Л. В. Шестакова. Информатика и ИКТ. Профильный уровень: учебник для 10 класса — М.: БИНОМ. Лаборатория знаний, 2012
Теоретический материал для самостоятельного изучения:
Давайте составим план, что бы мы хотели сделать с имеющейся у нас информацией.
Передавать — скорее всего, а может быть даже и продавать.
Обрабатывать и получать новую — вполне возможно!
Во всех трех случаях, которые называют основными информационными процессами, нам нужно информацию измерять.
В случае хранения, чтобы быть уверенными, что объем хранилища и объем нашей информации соответствуют друг другу, в передаче или продаже — чтобы объем продажи соответствовал цене, в случае обработки, чтобы рассчитать время, за которое этот объем может быть обработан.
Целью нашего урока будет определить способы измерения информации и сравнить их.
Для этого нужно будет определить:
— от чего зависит объем информации,
— какими единицами ее измерять.
Выявлять различия в подходах к измерению информации.
Применять различные подходы для измерения количества информации.
Переходить от одних единиц измерения информации к другим.
Предположим, что объем информации зависит от ее содержания. Нам нужна информация, которая для нас нова и понятна, соответствует всем свойствам информации, то есть та, которая приносит нам новые знания, решает наши вопросы.
Тут минимальным количеством информации будет ответ «да» или «нет». Ответ на такой простой вопрос принесет нам минимум информации и уменьшит неопределенность в два раза. Было два варианта, мы выбрали один и получили минимум информации — 1 бит.
Этот подход к измерению предложил К. Шеннон.
Информация (по Шеннону) — это снятая неопределённость. Величина неопределённости некоторого события — это количество возможных результатов (исходов) данного события. Сообщение, уменьшающее неопределённость знания в 2 раза, несёт 1 бит информации. Количество информации (i), содержащееся в сообщении об одном из N равновероятных результатов некоторого события, определяется из решения уравнения: 2i = N. Такой подход к измерению информации называют содержательным.
Разумно так же предположить, что текст, который для вас не понятен, понятен кому-то другому, то есть информация в нем все-таки есть. А ее объем зависит не от содержания текста, а от символов, которыми он написан. Назовем алфавитом все множество символов, используемых в языке, а их количество — мощностью алфавита.
Каждый символ, выбранный из алфавита, несет количество информации (i), вычисленное по формуле,
где N мощность алфавита.
Общее количество информации (I) во всем тексте можно посчитать по простой математической модели:
где k — количество символов в тексте.
Такой подход к измерению информации называют алфавитным. Здесь объем информации зависит от используемого алфавита и количества символов в тексте.
Этот подход к измерению информации предложил советский ученый-математик А. Н. Колмогоров.
Бит — мельчайшая единица информации. Для кодировки каждого из 256 символов, сведенных в таблицу кодировки ASCII, требуется 8 бит. Эта величина получила отдельное название — байт. Помимо бита и байта существуют более крупные единицы. Традиционно они получили приставки Кило, Мега, Гига и т. д.
Но Кило в единицах измерения информации обозначает не 10 3 =1000, а 2 10 =1024. Это недоразумение решается с конца XX века. Международная электротехническая комиссия предложила приставки «киби-, меби-, гиби-», которые лучше отражают смысл кратности степеням двойки.
Переводить единицы измерения информации можно при помощи удобной схемы
Определив подходы и единицы измерения, перейдем к оценкам. Сколько информации содержит книга? Библиотека? Видеоролик? Много? Это конечно, можно посчитать по уже известным нам простым формулам, а вот оценить «много» или «мало» не удастся, потому что это не количественные категории.
Сегодня существует понятие «большие данные». Так называют социально-экономический феномен, связанный с появлением технологических возможностей анализировать огромные массивы данных. Эти технологические возможности стремительно развиваются и уже позволяют компьютерам узнавать нас на фото, советуют нам какую музыку слушать и какие книги читать. Такси безошибочно находит нас в большом городе и проходит тестирование беспилотный транспорт.
Объемы данных, которыми оперирует человечество, исчисляется единицами зеттабайт, это единицы и 61 «0», к 2020 году по прогнозам это будет 40—44 зеттабайтов, а 2025 возрастет в 10 раз. Данные станут жизненно-важным активом, а их безопасность — критически важным вопросом.
Информацию можно измерять. Для этого существуют разные подходы, содержательный подход, алфавитный подход.
Суть содержательного подхода в том, что при определении объема информации учитывается содержание информации. Она должна быть новой и понятной получателю.
Суть алфавитного подхода в определении количества информации в зависимости от алфавита, которым она записана. А объем подсчитывается по формуле
где — объем информации,
— количество символов в сообщении,
— количество информации о каждом символе.
Для измерения количества информации в объеме данных используются единицы измерения информации.
Обработка данных важна для всех сфер жизни. Технологии обработки данных стремительно развиваются и становятся жизненно-важными.
Содержательный подход к измерению информации
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Бит — это минимальная единица измерения информации.
В одном бите содержится очень мало информации. Он может принимать только одно из двух значений (1 или 0, да или нет, истина или ложь). Измерять информацию в битах очень неудобно — числа получаются огромные. Ведь не измеряют же массу автомобиля в граммах.
Например, если представить объем флешки в 4Гб в битах мы получим 34 359 738 368 бит. Представьте, пришли вы в компьютерный магазин и просите продавца дать вам флешку объемом 34 359 738 368 бит. Вряд ли он вас поймет
Поэтому в информатике и в жизни используются производные от бита единицы измерения информации. Но у них у всех есть замечательное свойство — они являются степенями двойки с шагом 10.
Итак, возьмем число 2 и возведем его в нулевую степень. Получим 1 (любое число в нулевой степени равно 1). Это будет байт.
В одном байте 8 бит.
Теперь возведем 2 в 10-ю степень — получим 1024. Это килобайт (Кбайт).
В одном килобайте 1024 байт.
Если возвести 2 в 20 степень — получим мегабайт (Мбайт).
1Мбайт = 1024 Кбайт.
И так далее. Удобнее эти данные отобразить в виде таблицы:
Единицы измерения информации
В содержательном подходе количество информации, заключенное в сообщении, определяется объемом знаний, который это сообщение несет получающему его человеку.
Вы уже знаете, что за единицу измерения информации принимается 1 бит.
1 бит — минимальная единица измерения количества информации.
В теории информации для бита дается следующее определение:
Сообщение, уменьшающее неопределенность знания в два раза, несет 1 бит информации.
Что такое неопределенность знания, поясним на примерах.
В случае с монетой перед ее подбрасыванием неопределенность знания о результате равна двум.
Игральный же кубик с шестью гранями может с равной вероятностью упасть на любую из них. Значит, неопределенность знания о результате бросания кубика равна шести.
Следовательно, можно сказать так:
Вернемся к примеру с монетой. После того как вы бросили монету и посмотрели на нее, вы получили зрительное сообщение, что выпал, например, орел. Определился один из двух возможных результатов. Неопределенность знания уменьшилась в два раза: было два варианта, остался один. Значит, узнав результат бросания монеты, вы получили 1 бит информации.
Сообщение об одном из двух равновероятных результатов некоторого события несет 1 бит информации.
Пусть в некотором сообщении содержатся сведения о том, что произошло одно из N равновероятных событий.
Из математики известно, что решение такого уравнения имеет вид:
Если N равно целой степени двойки ( 2,4,8,16 и т. д.), то такое уравнение можно решить «в уме».
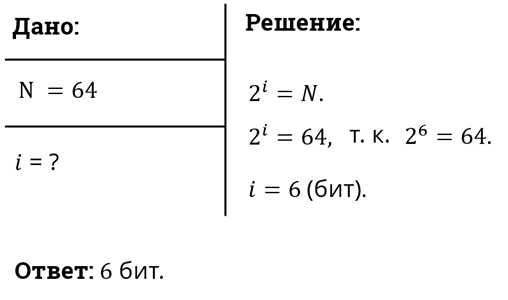
Шахматная доска состоит из 64 полей: 8 столбцов на 8 строк.
Какое количество бит несет сообщение о выборе одного шахматного поля?
Поскольку выбор любой из 64 клеток равновероятен, то количество бит находится из формулы:
i=log264=6, так как 26=64 .
Измерение информации. Содержательный подход
Урок 5. Информатика 10 класс (ФГОС)
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Измерение информации. Содержательный подход»
· содержательный подход к измерению информации;
· неопределённость знания об исходе некоторого события;
· единица измерения количества информации в рамках содержательного подхода.
Количество информации в одном том же сообщении, с точки зрения разных людей, может быть разным. Например, для человека, который не владеет английским языком, статья, напечатанная на английском языке, не несёт никакой информации. Информативным для человека является то сообщение, которое содержит новые и понятные сведения.
Давайте попробуем определить количество информации с позиции «информативно» или «неинформативно» для ученика 10 класса.
Столица России – Москва (это сообщение неинформативно, так как всем известно).
Высота Останкинской телебашни составляет 540 метров (или 45 этажей). Это делает её 6 по высоте конструкцией в мире (это сообщение информативно).
Корреляция, корреляционная зависимость — это зависимость между величинами, каждая из которых подвергается неконтролируемому разбросу (неинформативно, так как непонятно).
Необходимо отличать понятия информация и информативность.
Например, содержит ли учебник по информатике для десятого класса информацию? Конечно содержит, но для кого он будет информативным – для ученика десятого класса или первого класса? Естественно для ученика десятого класса. Первоклассник ничего из этого учебника не поймёт.
Теперь мы можем сделать вывод: количество информации зависит от информативности.
Информативность можно обозначить единицей, неинформативная информация равна нулю. Но это не даёт точного определения количества информации.
Алфавитный подход применяется для измерения информации, используемой компьютером. Так как компьютер не понимает смысла информации.
Содержательный подход применяется для измерения информации, используемой человеком.
В содержательном подходе, количество информации, заключённое в сообщении, определяется объёмом знаний, который это сообщение несёт получающему его человеку.
Тогда сущность содержательного подхода заключается в следующем: количество информации, заключённое в сообщении, должно быть тем больше, чем больше оно пополняет наши знания.
То есть, чем больше первоначальная неопределённость знания, тем больше информации несёт сообщение, снимающее эту неопределённость.
Допустим, вы бросаете монету, загадывая, что выпадет: орёл или решка. Есть всего два возможных результата бросания монеты.
Причём ни один из этих результатов не имеет преимущества перед другим. В таком случае говорят, что они равновероятны.
В данном случае с монетой, перед её подбрасыванием неопределённость знания о результате равна 2.
Если же бросать игральный кубик с шестью гранями, то он может с равной вероятностью упасть на любую из них. Значит, неопределённость знания о результате бросания кубика равна 6.
Или такая ситуация: спортсмены-бегуны перед забегом путём жеребьёвки определяют свои порядковые номера на старте. Допустим, что в забеге участвует 100 спортсменов, тогда неопределённость знания спортсмена о своём номере до жеребьёвки равна 100.
Вернёмся к спортсменам-бегунам.
Здесь событие – это жеребьёвка спортсменов; исход – спортсмену выпал, например, номер 34.
Итак, в первом примере возможны два варианта ответа: орёл, решка; во втором примере шесть вариантов: 1, 2, 3, 4, 5, 6.
В третьем примере – 100 вариантов, может выпасть номер от 1 до 100.
Теперь, согласно определению, можно сделать вывод, что наибольшее количество информации несёт третье сообщение, так как неопределённость знания об исходе события в этом случае была наибольшей.
В 40-х годах 20 века Клод Шеннон — американский учёный и инженер, один из создателей математической теории информации, решил проблему измерения информации.
Шеннон дал такое определение информации: Информация – это снятая неопределённость знания человека об исходе какого-то события.
Вернёмся к примеру, с монетой. После того как вы бросили монету и посмотрели на неё, вы получили зрительное сообщение, что выпал, например, орёл. Определился один из двух возможных результатов. Неопределённость знания уменьшилась в два раза: было два варианта, остался один. Значит, узнав результат бросания монеты, вы получили 1 бит информации.
Сообщение об одном из двух равновероятных результатов некоторого события несёт 1 бит информации.
А также сообщение, уменьшающее неопределённость знания об исходе некоторого события в два раза, несёт 1 бит информации.
Или такой пример. Вы подошли к светофору на пешеходном переходе, когда горел красный свет. Загорелся зелёный. Здесь вы также получили один бит информации.
Итак, мы выяснили, когда сообщение несёт 1 бит информации.
Значит в примерах с кубиком и спортсменами количество информации будет больше. Давайте выясним как измерить это количество.
Рассмотрим пример. Занятия могут состояться в одном из кабинетов, номера которых от одного до шестнадцати. Ученики спросили у учителя: «в каком кабинете будут проходить занятия?» На что учитель им ответил: «Угадайте ответ за четыре вопроса, на которые я могу дать ответ «Да» или «Нет»».
Подумав староста класса задала следующие вопросы:
1 вопрос. Номер кабинета меньше 9? – Да. Ответил учитель
2 вопрос. Номер кабинета больше 4? – Да.
3 вопрос. Номер кабинета чётный? – Нет.
4 вопрос. Номер кабинета 5? – Нет.
Ученики поняли, что занятия состоятся в кабинете номер 7.
Итак, сколько же информации получили ученики?
Первоначально неопределённость знания (количество возможных кабинетов) была равна 16. С ответом на каждый вопрос неопределённость знания уменьшалась в два раза и, следовательно, согласно данному выше определению, передавался 1 бит информации.
Первоначально было 16 вариантов. После первого вопроса осталось 8 вариантов, и ученики получили 1 бит информации.
После 2 вопроса осталось 4 варианта, и ученики получили ещё 1 бит информации.
После 3 вопроса осталось 2 варианта и был получен ещё 1 бит информации.
И, наконец после 4 вопроса, остался 1 вариант и получен ещё 1 бит информации.
То есть мы можем сделать вывод, что ученики получили четыре бит информации.
Такой способ нахождения количества информации, называется методом половинного деления: здесь ответ на каждый заданный вопрос уменьшает неопределённость знания, которая имеется до ответа на этот вопрос, наполовину. Каждый такой ответ несёт 1 бит информации.
Нужно отметить, что методом половинного деления наиболее удобно решать подобные проблемы. Таким способом всегда можно угадать, например, любой из 32 вариантов максимум за 5 вопросов.
Если бы поиск совершался последовательным перебором: «Мы будем заниматься в первом кабинете?» «Нет», «Во втором кабинете?» «Нет» и т. д., то про седьмой кабинет можно было бы узнать после семи вопросов, а про восьмой — после восьми.
Теперь мы можем полученные результаты описать с помощью следующих определений:
• сообщение об одном из двух равновероятных исходов некоторого события несёт 1 бит информации;
• сообщение об одном из четырёх равновероятных исходов некоторого события несёт 2 бита информации;
• сообщение об одном из восьми равновероятных исходов некоторого события несёт 3 бита информации.
Для того чтобы при измерении одной и той же информации получалось одно и то же значение количества информации, необходимо договориться об использовании определённого алфавита.
Пусть N – это количество возможных исходов события или неопределённость знания. Тогда i – это количество информации в сообщении об одном из N результатов.
Вернёмся к нашим примерам.
Обратите внимание, между данными величинами есть связь, которая выражается формулой.
Эта формула вам уже знакома. Также вы с ней встретитесь ещё не раз. Эта формула очень важна, поэтому её называют главной формулой информатики.
Для определения количества информации I, содержащейся в сообщении о том, что произошло одно из N равновероятных событий, нужно решить уравнение.
В математике такое уравнение называется показательным.
Рассмотрим пример. В коробке лежало 64 разноцветных катушки ниток. Сколько информации несёт сообщение о том, что из коробки достали жёлтую катушку?
Рассмотрим следующий пример.
В скором поезде Москва – Санкт-Петербург 8 вагонов, в каждом вагоне 32 места. Нужно определить какое количество информации несёт сообщение о том, что вам купили билет в 6 вагон, 13 место?
Этот пример показывает выполнение закона аддитивности количества информации (правило сложения): количество информации в сообщении одновременно о нескольких результатах независимых друг от друга событий равно сумме количеств информации о каждом событии отдельно.
Итак, мы уже говорили о том, что с формулой 2 i = N мы уже встречались на прошлом уроке, когда говорили об алфавитном подходе к измерению информации. Тогда N рассматривалось как мощность алфавита, a i — как информационный вес каждого символа алфавита.
Если допустить, что все символы алфавита появляются в тексте с одинаковой частотой, то есть равновероятно, то информационный вес символа i идентичен количеству информации в сообщении о появлении любого символа в тексте. При этом N — неопределённость знания о том, какой именно символ алфавита должен стоять в данной позиции текста. Это замечание показывает связь между алфавитным и содержательным подходами к измерению информации.
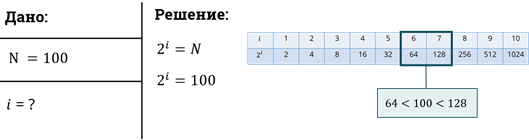
Рассмотрим пример: Требуется угадать задуманное число из диапазона целых чисел, например, от 1 до 100. Чему равно количество информации в сообщении о том, что загаданное число 89?
То есть, если значение N равно целой степени двойки, то показательное уравнение легко решить, а если нет, как в нашем примере. Как поступить в этом случае?
Можно догадаться, что решением уравнения будет дробное число, которое находится между 6 и 7.
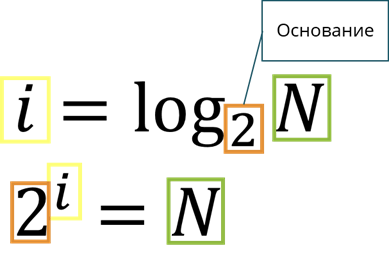
В математике существует функция, с помощью которой решаются показательные уравнения. Эта функция называется логарифмом.
Тогда решение показательного уравнения запишется i равно логарифм N по основанию 2. Это означает, что мы должны найти степень, в которую нужно возвести основание, в нашем случае 2, чтобы получить N.
Например, для целых степеней двойки получим:
Значения логарифмов находятся с помощью специальных логарифмических таблиц. Также можно использовать инженерный калькулятор или табличный процессор.
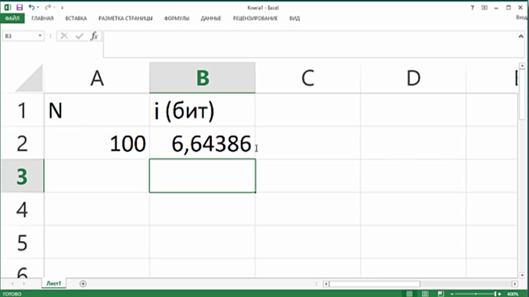
Определим количество информации, полученной из сообщения об угадывании задуманного числа из диапазона от одного до ста, с помощью электронной таблицы.
Количество информации в сообщении о том, что загаданное число 89 приблизительно равно 6,64 бит.
Формула для измерения количества информации была предложена американским учёным-электронщиком Ральфом Хартли, который является одним из основоположников теории информации.
Данный пример показал, что количество информации, определяемое с использованием содержательного подхода, может быть дробной величиной, если же находить информационный объем, путём применения алфавитного подхода, то там может быть только целочисленное значение.
В содержательном подходе количество информации, заключённое в сообщении, определяется объёмом знаний, который это сообщение несёт получающему его человеку.
Сообщение, уменьшающее неопределённость знания в два раза, несёт один бит информации.
Для измерения количества информации применяется формула Хартли: 