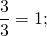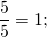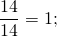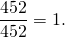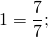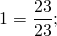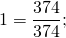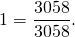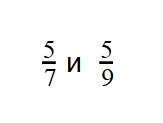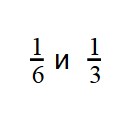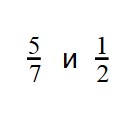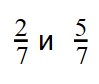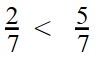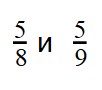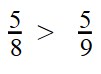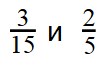что делать если числитель и знаменатель одинаковые

Числитель равен знаменателю

Что можно сказать о дроби, у которой числитель равен знаменателю?

Знаменатель обыкновенной дроби показывает, на сколько долей (частей) разделили одно целое, а числитель — сколько таких частей взяли.

Если числитель и знаменатель равны, то получается, что число разделили на части и все эти части взяли.

То есть одно целое осталось.

Значит, дробь, у которой числитель равен знаменателю, равна единице.

Если в результате вычислений получается дробь, у которой числитель и знаменатель равны, ее надо упростить, записав равной единице.

Обратно, единицу можно представить в виде дроби с любыми равными между собой числителем и знаменателем.

Это свойство единицы используется при сложении и вычитании дробей и смешанных чисел.

Источник

Вычитание дробей

4 класс, 5 класс, 6 класс

Понятие дроби

Дробь — одна из форм представления числа в математике. Это запись, в которой a и b являются числами или выражениями. Есть два формата записи:

Над чертой принято писать делимое, которое является числителем. А под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.

Дроби бывают двух видов:

Дробь называют правильной, когда ее числитель меньше знаменателя. Например 3/7 и 31/45.

Неправильной — ту, у которой числитель больше знаменателя или равен ему. Например, 21/4. Такое число является смешанным и читается, как пять целых одна четвертая, а записывается — 5 1\4.

Основные свойства дробей

1. Дробь не имеет значения, при условии, если делитель равен нулю.

2. Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.

3. Равными называют a/b и c/d в том случае, если a * d = b * c.

4. Если числитель и знаменатель умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

Правило вычитания дробей

Вычитание — арифметическое действие, когда от одного числа отнимают другое.

Свойства вычитания:

Записывайтесь на наши дополнительные занятия по математике, для учеников с 1 по 11 классы!

Вычитание дробей с одинаковыми знаменателями

Для вычитания дробей с одинаковыми знаменателями нужно от числителя первой отнять числитель второй, а знаменатель оставить тот же.

Прежде, чем зафиксировать ответ, важно проверить возможность сокращения.

Рассмотрим это правило на примере:

Вычитание дробей с разными знаменателями

Как вычитать дроби с разными знаменателями? Для этого приводим их к общему знаменателю и гаходим разность числителей.

Рассмотрим пример, в котором нужно найти разность 2/9 и 1/15.

Как решаем:

НОК (9, 15) = 3 * 3 * 5 = 45

Вычитание обыкновенной дроби из натурального числа

Для вычитания из обыкновенной дроби натурального числа необходимо это действие привести к вычитанию обыкновенных дробей.

Разберем для наглядности пример разности 3 и 6/7.

Как решаем:

Ответ: две целых одна седьмая.

Вычитание натурального числа из обыкновенной дроби

Для вычитания натурального числа из обыкновенной дроби нужно последовать тому же алгоритму, что и в предыдущем примере. А именно: перевести натуральное число в вид дроби, привести все к единому знаменателю, найти разность.

Рассмотрим пример разности 3 из 83/21.

Как решаем:

А еще можно вот так:

Если урок в самом разгаре и посчитать нужно быстро — можно воспользоваться онлайн-калькулятором. Вот несколько подходящих:

Прибавление и вычитание дробей — смежные темы: принципы и закономерности очень похожи. Чтобы закрепить знания, нужно решать примеры сложения дробей, как можно чаще.

Источник

Сравнение дробей, как правильно

Сравнение дробей с одинаковыми знаменателями

Как и при любом другом сравнении, суть сравнения дробей — в том, чтобы определить меньшую и большую дроби.

Нет ситуации более благоприятной для сравнения, чем дроби с одинаковыми знаменателями. Если вся разница между дробями только в числителях, пользуемся следующим правилом:

Из двух дробей с одинаковыми знаменателями больше дробь с большим числителем. А меньше будет та дробь, числитель которой меньше.

А теперь на примерах.

Пример 1. Сравните дроби:

Пример 3. Сравните дроби:

Как видите, нет ничего сложного в сравнении дробей, если знаменатели равны. Вся задача заключается в том, чтобы определить больший и меньший знаменатель.

Давайте разберем наглядный пример сравнения дробей:

Допустим, в торте 6 кусков. Если от целого торта отрезать один кусок — в торте останется 5 кусков.

Понять, что целый торт больше, чем торт без одного куска, можно и без сравнения дробей. Но это же самое правило можно применить и при менее очевидных сравнениях, которые часто встречаются в повседневной жизни.

Сравнение дробей с одинаковыми числителями

Вы уже разобрались со сравнением дробей с одинаковыми знаменателями. Теперь задача чуть усложняется — научимся сравнивать дроби с разными знаменателями, но с одинаковыми числителями.

Если у двух дробей одинаковые числители, то больше будет та дробь, чей знаменатель меньше. А меньше будет дробь с большим знаменателем.

А теперь наши любимые примеры. Погнали!

Пример 1. Сравните дроби:

Пример 3. Сравните дроби:

Сравнение дробей с разными числителями и разными знаменателями

Нет ничего хитрого в сравнении дробей с одинаковыми числителями или знаменателями. Чуть больше усилий потребуется при сравнении дробей, в которых нет ничего одинакового.

Сначала вспомним, как привести дроби к общему знаменателю.
Рассмотрим пример дробей с разными знаменателями.

Давайте потренируемся в сравнении дробей.

Пример 1. Сравните дроби:

При сравнении неправильных дробей, помните, что неправильная дробь всегда больше правильной.

Пример 2: Сравните дроби:

Вычитание смешанных чисел

Вычитание проходит гладко, когда уменьшаемое больше вычитаемого.

В случае, если вычитаемое больше уменьшаемого, разность оказывается отрицательной. В этом нет ничего страшного. Но математика в 5 классе — «положительная», поэтому научимся находить разность смешанных чисел, не скатываясь «в минусы».

При вычитании дробей действует тот же самый принцип: вычитаемое должно быть больше уменьшаемого. Вот здесь то вам и пригодится навык сравнивать дроби.

Пример 1. Найдите разность:

Вычитаемая дробь меньше уменьшаемой

Пример 2.Найдите разность:

Если знаменатели одинаковые — больше та дробь, числитель которой больше.

Примеры для самопроверки

Теория — это, конечно, хорошо. Но без практики — никуда. Пора потренироваться в решении примеров и закрепить тему сравнения дробей.

Пример 1. Сравните дроби:

Ответ: по правилу сравнения дробей с одинаковыми знаменателями, больше та дробь, у которой числитель больше. Это значит, что

Пример 2. Сравните дроби:

Ответ: по правилу сравнения дробей с разными знаменателями и одинаковыми числителями, больше та дробь, чей знаменатель меньше. Это значит, что

Пример 3. Сравните дроби:

Ответ:.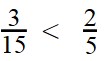

Источник

Дроби. Вычитание дробей.

Вычитание дробей с одинаковыми знаменателями.

Для нахождения разницы 2х дробей с одинаковыми знаменателями, необходимо вычесть из числителя 1й дроби числитель 2й дроби, а знаменатель обоих дробей оставить не изменяя. Вычитание обыкновенных дробей:

Обратите внимание! Перед тем как написать окончательный ответ, посмотрите, может можно сократить дробь, которую вы получили.

Вычитание дробей с одинаковыми знаменателями, примеры:

,

,

Вычитание правильной дроби из единицы.

Если необходимо вычесть из единицы дробь, которая является правильной, единицу переводят к виду неправильной дроби, у нее знаменатель равен знаменателю вычитаемой дроби.

Пример вычитания правильной дроби из единицы:

Знаменатель вычитаемой дроби = 7, т.е., единицу представляем в виде неправильной дроби 7/7 и вычитаем по правилу вычитания дробей с одинаковыми знаменателями.

Вычитание правильной дроби из целого числа.

Правила вычитания дробей – правильной из целого числа (натурального числа) :

Вычтем из целого числа правильную дробь: представляем натуральное число в виде смешанного числа. Т.е. занимаем единицу в натуральном числе и переводим её к виду неправильной дроби, знаменатель при этом такой же, как у вычитаемой дроби.

Пример вычитания дробей:

В примере единицу мы заменили неправильной дробью 7/7 и вместо 3 записали смешанное число и от дробной части отняли дробь.

Вычитание дробей с разными знаменателями.

Или, если сказать другими словами, вычитание разных дробей.

Правило вычитания дробей с разными знаменателями. Для того, чтобы произвести вычитание дробей с разными знаменателями, необходимо, для начала, привести эти дроби к наименьшему общему знаменателю (НОЗ), и только послеиэтого произвести вычитание как с дробями с одинаковыми знаменателями.

Общий знаменатель нескольких дробей — это НОК (наименьшее общее кратное) натуральных чисел, которые являются знаменателями данных дробей.

Внимание! Если в конечной дроби у числителя и знаменателя есть общие множители, то дробь необходимо сократить. Неправильную дробь лучше представить в виде смешанной дроби. Оставить результат вычитания, не сократив дробь, где есть возможность, — это незаконченное решение примера!

Порядок действий при вычитании дробей с разными знаменателями.

Таким же образом проводится сложение и вычитание дробей при наличии в числителе букв.

Вычитание дробей, примеры:

Вычитание смешанных дробей.

При вычитании смешанных дробей (чисел) отдельно из целой части вычитают целую часть, а из дробной части вычитают дробную часть.

Первый вариант вычитания смешанных дробей.

Если у дробных частей одинаковые знаменатели и числитель дробной части уменьшаемого (из него вычитаем) ≥ числителю дробной части вычитаемого (его вычитаем).

Второй вариант вычитания смешанных дробей.

Когда у дробных частей разные знаменатели. Для начала приводим к общему знаменателю дробные части, а после этого выполняем вычитание целой части из целой, а дробной из дробной.

Третий вариант вычитания смешанных дробей.

Дробная часть уменьшаемого меньше дробной части вычитаемого.

Т.к. у дробных частей разные знаменатели, значит, как и при втором варианте, сначала приводим обыкновенные дроби к общему знаменателю.

В числителе от правой части пишем сумму числителей, дальше раскрываем скобки в числителе от правой части, то есть умножаем все и приводим подобные. В знаменателе скобки не раскрываем. В знаменателях принято оставлять произведение. Получаем:

Источник

Деление дробей: теория и практика

Понятие дроби

Дробь — одна из форм представления числа в математике. Это запись, в которой a и b являются числами или выражениями. Существует два формата записи:

Над чертой принято писать делимое, которое является числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление. В 5 классе ребята это уже знают.

Дроби бывают двух видов:

Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 3/7 и 31/45.

Неправильной — ту, у которой числитель больше знаменателя или равен ему. Например, 21/4. Такое число является смешанным и читается, как пять целых одна четвертая, а записывается — 5 1\4.

Основные свойства дроби

1. Дробь не имеет значения, при условии, если делитель равен нулю.

2. Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.

3. Две дроби a/b и c/d называются равными, если a * d = b * c.

4. Если числитель и знаменатель умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

Деление дробных чисел

Деление — арифметическое действие, по которому можно узнать, сколько раз одно число содержится в другом. А еще деление — это обратное действие умножения.

Свойства деления:

1. При делении на единицу получится такое же число:

2. На ноль делить нельзя.

3. Когда делим ноль на любое число, всегда получаем ноль:

4. Когда делим любое число на само себя получаем единичку:

5. Когда делим сумму на какое-либо число, можно разделить на него каждое слагаемое, а потом сложить полученное:

6. Когда делим разность на какое-нибудь число, можно разделить на него уменьшаемое и вычитаемое отдельно и из первого частного вычесть второе:

7. Когда делим произведение двух множителей на число, можно разделить на него любой из множителей и частное умножить на второй множитель:

Записывайся на онлайн обучение по математике, с лучшими учителями! Для учеников с 1 по 11 классы!

Деление обыкновенных дробей

Как делить дробь на дробь? Выполняем следующую последовательность действий:

Другими словами это правило звучит так: чтобы разделить одну дробь на другую, надо первую умножить на обратную от второй.

Как делить дроби с разными знаменателями? Тут все просто: пользуемся правилами выше, поскольку на практике нам неважно, одинаковые знаменатели или нет.

Деление дроби на натуральное число

Для деления дроби на натуральное число нужно:

Деление натурального числа на дробь

Чтобы поделить натуральное число на обыкновенную дробь нужно:

Деление на смешанное число

Для деления смешанных чисел необходимо:

Если урок в самом разгаре и посчитать нужно быстро — можно воспользоваться онлайн-калькулятором. Вот несколько подходящих:

Источник