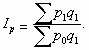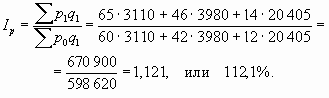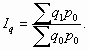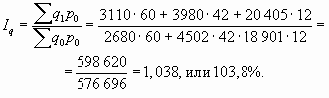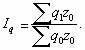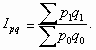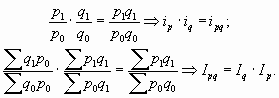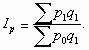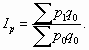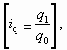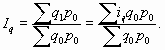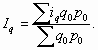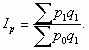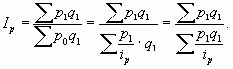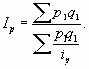что такое агрегатная форма
Агрегатная форма общего индекса
Поможем написать любую работу на аналогичную тему
Агрегатная форма является основной. В переводе с латинского «агрегатная форма» означает присоединение, то есть и к числителю и к знаменателю индивидуальных индексов добавляется соизмеритель (вес). Он необходим для перехода от натуральных показателей к стоимостным.
При выборе веса индекса следует руководствоваться следующим правилом: если строится индекс количественного показателя, то веса берутся за базисный период, если строится индекс качественного показателя, то используется вес отчетного периода.
Отличительной особенностью любого агрегатного индекса является то, что в числителе и знаменателе его фигурирует сумма произведений двух показателей, один из которых меняется, т.е. выступает в роли индексируемой величины, а второй остается неизменным, т.е. выступает в роли соизмерителя. Рассмотрим построение общих индексов.
1. Индекс физического объема ( Iq )
Он показывает, во сколько раз возросла (уменьшилась) стоимость продукции из-за роста (снижения) объема производства или показывает сколько процентов составляет рост (снижение) стоимости продукции в результате изменения физического объема ее производства.
Это индекс качественного показателя. Он показывает, во сколько раз возросла (уменьшилась) стоимость продукции из-за изменения цен, или сколько процентов составляет рост (снижение) стоимости продукции в результате изменения цен.
3. Общий индекс стоимости ( Ipq )
Он показывает, во сколько раз возросла (уменьшилась) стоимость продукции отчетного периода по сравнению с базисным, или сколько процентов составляет рост (снижение) стоимости продукции.
Разность между числителем и знаменателем показывает на сколько в денежном выражении увеличилась или уменьшилась стоимость продукции в отчетном периоде, по сравнению с базисным за счет изменения индексируемой величины.
За счет изменения объемного показателя 
, за счет изменения качественного показателя (например, цены) 
, за счет изменения и объемного и качественного показателя 
.
14. Агрегатная форма общего индекса. Правила взвешивания общих индексов
Агрегатная форма общего индекса качественных показателей.
где р — индексируемая величина (цена);
q — количество проданных товаров в натуральном выражении (веса).
В настоящее время именно эта формула используется при изучении динамики цен. Этот индекс характеризует изменение цен в среднем по совокупности товаров в отчетном периоде по сравнению с базисным.
Общий индекс цены можно также определить по формуле Пааше :
Эта формула длительное время использовалась в СССР при изучении динамики цен. Но с переходом к рыночной экономике стала существенно изменяться структура потребительских расходов населения, т. е. на динамику цен существенное влияние стало оказывать изменение параметра q.
Правило взвешивания общих индексов качественных показателей.
Общий индекс качественных показателей в агрегатной форме взвешивается по весам отчетного периода. Например, общий индекс себестоимости в агрегатной форме:
Общий индекс урожайности в агрегатной форме:
Агрегатная форма общих индексов количественных показателей. Рассмотрим агрегатную форму общего индекса физического объема товарооборота (q). Iq может быть построен по формуле Ласпейраса, которая является основной:
Данный индекс характеризует изменение физического объема товарооборота в среднем по совокупности товаров. Возможно также построение Iq по формуле Пааше:
Правило взвешивания общего индекса количественных показателей. Данные индексы взвешиваются по весам базисного периода.
Например, общий индекс посевной площади в агрегатной форме:
Агрегатная форма индекса.
Понятие об индексах.
Слово «index» латинское и означает «показатель», «указатель». В статистике под индексом понимается обобщающий количественный показатель, выражающий соотношение двух совокупностей, состоящих из элементов, непосредственно не поддающихся суммированию. Например, объем продукции предприятия в натуральном выражении суммировать нельзя (кроме однородной), а для обобщающей характеристики объема это необходимо. Нельзя суммировать цены на отдельные виды продукции и т.д. Для обобщающей характеристики таких совокупностей в динамике, в пространстве и по сравнению с планом применяются индексы. Кроме сводной характеристики явлений индексы позволяют дать оценку роли отдельных факторов в изменении сложного явления. Индексы используются и для выявления структурных сдвигов в народном хозяйстве.
Индексы рассчитываются как для сложного явления (общие или сводные), так и для отдельных его элементов (индивидуальные индексы).
Индивидуальные индексы представляют собой отношение отдельных элементов совокупности. Это обычная относительная величина. Например, если цена товара в текущем периоде 30 руб., а в базисном была 25 руб., то индивидуальный индекс будет равен 
или 120%.
В зависимости от объекта исследования как общие, так и индивидуальные индексы подразделяются на индексы объемных (количественных) показателей (физического объема продукции, посевной площади, численности рабочих и др.) и индексы качественных показателей (цены, себестоимости, урожайности, производительности труда, заработной платы и др.).
В зависимости от базы сравнения индивидуальные и общие индексы могут быть цепными и базисными.
В зависимости от методологии расчета общие индексы имеют две формы: агрегатную и форму среднего индекса.
Агрегатная форма индекса.
Агрегатная форма сводного индекса является основной. От нее происходят все остальные сводные индексы.
В дальнейшем изложении будут использованы следующие обозначения:
«х» может принимать значения:
«d» может принимать значения:
Для построения сводных индексов в агрегатной форме следует помнить следующие правила:
2. Вес (соизмеримость) остается неизменным, т.е. одинаковым в числителе и знаменателе (кроме случая, когда индексируемой величиной является все произведение);
3. В индексах качественных показателей индексируемая величина качественный показатель («х»), а весом является количественный показатель («d»), который берется неизменным в числителе и знаменателе на уровне отчетного периода («1»);
Тогда индексы всех качественных индексов (кроме исключения) в общем виде можно записать в виде формулы 
, а изменение в абсолютном выражении как разность 
.
Качественные индексы конкретных показателей:
Индекс производительности труда по трудоемкости (исключение).
Разность 
свидетельствует об экономии труда за счет роста производительности труда, если «-«, дополнительных затратах труда за счет снижения его производительности, если «+».
Индекс трудоемкости 
. Разность 
изменение затрат за счет трудоемкости.
Индексы количественных показателей в общем виде 
, а изменение в абсолютном выражении 
.
Конкретные количественные индексы:
Индекс физического объема в зависимости от исходной информации может иметь три различных веса. Если весом является цена, то 
, где 
— отчетный объем продукции (или товарооборота) в базисных ценах,
Индекс посевной площади 
. Разность 
показывает изменение валового сбора за счет изменения размера посевных площадей.
Индекс численности рабочих (работников) также может быть рассчитан в двух вариантах в зависимости от веса. Если весом является выработка, то 
, а разность 
характеризует изменение объема продукции за счет изменения численности. Если весом является заработная плата, то 
, а разность 
показывает экономию (если «-«) или перерасход (если «+») фонда оплаты труда за счет соответственно сокращения или увеличения численности рабочих (работников).
Если индексируемой величиной является вся сложная совокупность (товарооборот, валовой сбор, фонд оплаты труда, издержки производства и т.д.), то оба сомножителя в числителе отчетного периода, а в знаменателе базисного периода. В общем виде 
.
Индекс товарооборота 
;
Индекс издержек (затрат) на производство 
;
Индекс валового сбора 
;
Индекс фонда оплаты труда 
;
Индекс затрат труда 
;
Разность числителя и знаменателя индекса 
характеризует общее изменение сложной совокупности.
Индексы в статистике
10.3. Агрегатные индексы
При использовании индексного метода на практике чаще всего решают задачу нахождения не индивидуальных, а сводных индексов. Общий (сводный) индекс (I) представляет собой отношение уровней сложного экономического явления, состоящего из элементов, непосредственно несоизмеримых. Он дает обобщающую характеристику изменения одноименного показателя по разнородной совокупности во времени, в пространстве или по сравнению с некоторым заданным уровнем (например, планируемым или нормативным).
В индексной теории по способу (форме) построения общие (сводные) индексы подразделяют на агрегатные, средние и индексы изменения среднего показателя. Последняя группа индексов имеет свою специфику, о ней мы будем говорить ниже.
Основной формой построения индексов является агрегатная; средние индексы получаются в результате ее преобразования. В агрегатной формуле сводного индекса присутствуют два элемента:
Веса в общем индексе необходимы, поскольку суммировать значение признака х по элементам разнородной совокупности неправомерно (например, нельзя суммировать объемы продаж различных товаров в розничной торговле в натуральных единицах измерения). Поэтому находят такой связанный с х показатель (f), при котором произведение х и f имеет экономическое содержание и может суммироваться по всем единицам разнородной совокупности [например, умножив количества товаров на их цены, получим объемы продаж в денежном выражении (товарооборот), которые можно суммировать по разным видам товаров].
Общая формула агрегатного индекса может быть записана следующим образом:
Такое построение агрегатных индексов позволяет получить систему взаимосвязанных индексов и провести анализ влияния отдельных факторов на изменение обобщающих результативных показателей.
Пример 10.2. В таблице представлена следующая информация по ценам и количеству проданной молочной продукции:
| Наименование товара | Единицы измерения | Цена, руб. | Количество проданного товара | ||
|---|---|---|---|---|---|
| базисный период | отчетный период | базисный период | отчетный период | ||
| Масло | кг | 60 | 65 | 2 680 | 3 110 |
| Сметана | кг | 42 | 46 | 4 502 | 3 980 |
| Цельное молоко | л | 12 | 14 | 18 901 | 20 405 |
Проведем расчет общего индекса цен по агрегатной формуле.
Следовательно, цены на молочную продукцию увеличились в 1,121 раза, или на 12,1%. Агрегатная форма построения индекса позволяет провести расчеты с учетом веса каждого товара в их общей совокупности.
Тогда в числителе и знаменателе получим товарооборот соответствующих периодов, выраженный в ценах базисного периода. Индекс покажет, как изменился товарооборот в отчетном периоде по сравнению с базисным в результате снижения или роста физического объема продаж (аналитический подход) или как в среднем увеличился или снизился физический объем товарооборота в отчетном периоде по сравнению с базисным (синтетический подход).
Пример 10.3. По данным таблицы из примера 10.2 определим изменения объема продаж молочной продукции. Для этого рассчитаем общий индекс физического объема товарооборота.
Таким образом, в среднем физический объем товарооборота молочной продукции увеличился в 1,038 раза, или на 3,8%.
Индекс физического объема рассчитывается при анализе не только товарооборота, но и изменения издержек производства (затрат). В этом случае соизмерителем выступит уже себестоимость единицы продукции (остальные принципы построения индекса останутся прежними):
Агрегатные индексы результативных показателей, получаемых как произведение определенных величин, имеют несколько иной вид. В качестве примера приведем индекс товарооборота (стоимости) продукции. В этом случае сравниваются объемы товарооборота отчетного и базисного периодов, при этом не требуется введения каких-либо соизмерителей, поскольку значения уже сопоставимы и их можно суммировать по разным видам товаров. Агрегатный индекс товарооборота получается как простое соотношение его суммарных значений по группам товаров за разные периоды времени:
Пример 10.4. По данным таблицы из примера 10.2 определим общий индекс товарооборота.
То есть товарооборот (объем проданной молочной продукции в денежном выражении) увеличился в 1,163 раза, или на 16,3%.
Аналогичным образом рассчитывают агрегатные индексы и других результативных показателей. Например, издержки производства можно представить как произведение себестоимости единицы продукции на объем ее производства в натуральном выражении (zq). Агрегатный индекс издержек обращения имеет вид
Например, если из числителя сводного индекса товарооборота вычесть знаменатель (
) то получим величину, определяющую, на сколько денежных единиц изменился товарооборот в отчетном периоде по сравнению с базисным.
Аналогично индекс затрат на производство продукции является произведением индекса себестоимости и индекса физического объема продукции:
Следует отметить, что в теории и практике статистики существует несколько подходов к решению проблемы выбора системы взвешивания. В частности, при построении агрегатных индексов цен используется несколько формул расчета этих показателей, названных по имени авторов, их разработавших. Наибольшую известность получили индексы цен Пааше, Ласпейреса и Фишера.
При расчете индекса цен по формуле Пааше в качестве весов берутся количества продукции текущего периода:
С помощью этого индекса определяется изменение цен на товары, реализованные или приобретенные в текущем периоде.
При расчете индекса цен по формуле Ласпейреса в качестве весов используются количества продукции базисного периода:
Данный индекс характеризует изменение цен на товары, реализованные в базисном периоде. По такой схеме обычно строятся индексы стоимости жизни, когда хотят оценить изменение цен на фиксированный набор товаров, обычно приобретаемых определенными группами населения.
В данной формуле равноправно представлено количество продукции как базисного, так и текущего периодов. Это свойство позволяет применять данный индекс при исследовании цен за значительный промежуток времени, когда структура продукции претерпевает существенные изменения, и, строго говоря, не представляется возможным сделать обоснованный выбор в пользу весов базисного или отчетного периода. По этим же соображениям индекс Фишера часто используется для территориальных сопоставлений.
10.4. Средние индексы
В отличие от агрегатной формы индекса, средние индексы используются тогда, когда имеется информация об изменении индексируемой величины по отдельным единицам исследуемой совокупности (т.е. известны индивидуальные индексы).
Средний индекс получают путем преобразования агрегатного индекса. В зависимости от того, какие веса используются в соответствующей агрегатной формуле (базисного или отчетного периода), средний индекс рассчитывается по формуле средней арифметической или средней гармонической величины. Соответственно, исчисленные по одним и тем же данным агрегатный и средний индексы всегда равны.
Рассмотрим, например, как получается средний индекс физического объема товарооборота. Его агрегатная формула имеет вид
Тогда, учитывая, что индивидуальный индекс представляет собой отношение
получим [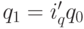 
]. Подставим это выражение в формулу агрегатного индекса
Получен индекс физического объема товарооборота в виде средней арифметической взвешенной из индивидуальных индексов, в которой в качестве весов используется товарооборот базисного периода (q0 p0).
Итак, формула среднего арифметического индекса физического объема имеет вид
Обратимся теперь к индексу цен. Его агрегатная формула имеет вид
Из формулы индивидуального индекса цен 
выразим 
и, подставив в формулу агрегатного индекса, получим
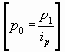
Получен средний гармонический индекс цен
Пример 10.5. По данным таблицы из примера 10.2 рассчитаем средние индексы. Для этого необходимо определить индивидуальные индексы и объем товарооборота по каждому виду молочной продукции (расчеты проведены в следующей таблице).
 |
Исчислим средний гармонический индекс цен.
Средний арифметический индекс физического объема товарооборота равен