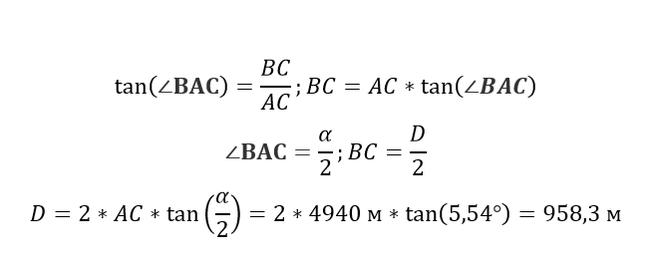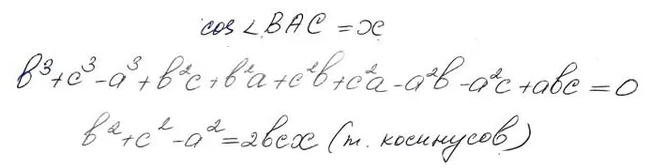что такое аксиома в математике
Так ли точна математика, как кажется?
Наверное, данный вопрос задавал себе каждый, чуточку интересующийся математикой человек. Прочитав статью 2 х 2 = 4, было сделано заключение, что эта тема также может понравиться хабралюдям. Речь пойдет об аксиомах в математике, противоречиях и парадоксах. Кому интересно — добро пожаловать под кат.
Вместо предисловия
Каждый из нас в школе не сомневался в справедливости тех или иных математических утверждений. Ну и правда, что учитель сказал, то и истина. Но, познакомившись со строгой математикой (не люблю слово «высшей»), мы начали понимать, что чем больше мы стараемся формализовать предмет, тем сложнее это сделать, а иногда совсем не получается.
Так нам привычные действительные числа, для Леопольда Кронекера не являлись таковыми, он говорил: «Бог создал натуральные числа, а всё прочее — дело рук человеческих» («Die ganzen Zahlen hat der liebe Gott gemacht, alles andere ist Menschenwerk»)
После того, как Георг Кантор доказал, что отрезок равномощен (А и B равномощны, если существует биекция между ними) n-мерному пространству, он провозгласил: «Я вижу это, но я не верю в это!» («Je le vois, mais je ne le crois pas!»)
Немного философии
Речь в этой статье пойдет об аксиоматике тех или иных математических множеств, операций и т.д., но все же закономерным вопросом будет, а зачем нам аксиомы вообще нужны? Приведу простой пример. Возьмем русский язык и слово, например, «дежавю». Посмотрим его значение, «Дежавю́ — психическое состояние, при котором человек ощущает, что он когда-то уже был в подобной ситуации». Но мы дотошные, посему теперь вместо одного слова перед нами возникнет куда больше. Что такое «психический», «состояние», «человек», «ощущать», «подобный», «ситуация». Как вы можете заметить, у нас получается дерево слов, а в силу того, что слов, имеющих значение в русском языке конечное множество, у нас получится путь в дереве, в котором встречается дважды одно и то же слово, т.е. мы определили его через самого себя.
Вот для этого и нужны аксиомы. Нам всегда нужен фундамент, с которого мы можем стартовать, что-то, что и так всем интуитивно понятно. Неточность 1. В математике часто бывают утверждения, интуитивно понятные, но приводящие к парадоксам. Например аксиома выбора(Axiom of Choice), но об этом мы поговорим чуть позже.
Больше конкретики. Аксиомы Пеано натуральных чисел.
Я, как программист, люблю считать, что 0 принадлежит натуральным числам, это удобно. Что-ж, теперь наиболее знаменитая аксиоматика Пеано.
1. 0 является натуральным числом.
2. Число, следующее за натуральным, тоже является натуральным.
3. 0 не следует ни за каким натуральным числом.
4. Если натуральное число a непосредственно следует как за числом b, так и за числом c, то b и c совпадают.
5. (Аксиома индукции) Если какое-либо предложение доказано для 0 (база индукции) и если из допущения, что оно верно для натурального числа n, вытекает, что оно верно для следующего за n натурального числа (индукционное предположение), то это предложение верно для всех натуральных чисел.
Разберемся по-порядочку.
1-я аксиома говорит, что существует хотя бы одно натуральное число. Иначе бы мы сказали, что это вообще пустое множество и все аксиомы бы для него выполнялись бы.
2 и 3 вроде бы и так ясны.
4. Эта аксиома нужна для того, чтобы не появились «ответвления». Иначе мы могли бы сказать, что 3 следует за 2 и 2′, а дальше 2 и 2′ за 1 и 1′ соответственно, и т.д. В принципе, такая модель имеет право на существование, но на ней крайне сложно ввести отношение порядка.
5. Первый человек в очереди женщина. За каждой женщиной идет женщина. В реальной жизни это значит, что вся очередь состоит из женщин. А так как мы хотим описывать все же более жизненные объекты, то и вводим аксиому индукции, ибо из предыдущих она никак не следует.
Удобная модель, все отлично, все счастливы. Вопрос, в чем же подвох? Оказывается, что если мы добавим новое натуральное число с к нашим привычным натуральным числам и скажем, что оно больше всех наших привычных, то мы не придем ни к какому противоречию. Т.е. у нас есть не только наша модель N, но и, к примеру, N + Z. Где в N и Z (целые числа) обычное сравнение чисел, а также любое число из N меньше любого числа из Z.
Вопрос, можно ли ввести аксиомы так, чтобы мы описали наши привычные натуральные числа, и только их (т.е. существует ли формула, подставив в которую естественное натуральное число она выдаст True, а любое другое число False)? Ответ — нет. Идея доказательства в том, что все формулы можно закодировать натуральными числами. А далее, написав хитрую формулу, и подставив ее код в Ф (формула, которая по предположению умеет определять естественную натуральность), мы получим противоречие.
Больше конкретики. Аксиоматика множеств Цермело-Френкеля (ZF)
1. Аксиома объемности. Если два множества состоят из одинаковых элементов, то они равны.
2. Аксиома подмножеств. Если у нас есть некоторая формула, то из любого множества она «вырезает» также множество.
3. Аксиома замены. Если для каждого мн-ва х, F(x) = также является множеством, то для любого а, — также множество.
4. Аксиома степени. Множество подмножеств также является множеством.
5. Аксиома бесконечности. Существует множество, которое содержит пустое множество, а также вместе с каждым элементом x содержит множество <
6. Аксиома регулярности. Не существует бесконечных по включению цепочек множеств, т.е. нельзя, чтобы множество a1 сожержало a2, то в свою очередь a3, и т.д.
Противоречия и парадоксы
Во-первых, не доказано, что аксиомы ZF непротиворечивы, если же они противоречивы, то можно вывести любое утверждение, например 0 = 1, и грош цена нашей науке. Даже более, доказано, что нельзя доказать непротиворечивость ZF. Забавная штука получается, но в этом нет ничего страшного. Если мы чего-то не можем доказать, не значит, что этого нет, в данном случае непротиворечивости. Движемся дальше.
Математика получается достаточно скупой наукой, то есть мало всего можно доказать, если не добавить аксиому выбора. А что это за аксиома такая? В трех словах — из любого непустого множества можно выбрать элемент. Казалось бы, очень естественная аксиома, но она приводит к парадоксу Банаха-Тарского, заключающегося в том, что шар можно разбить на 5 кусков и собрать из них 2 таких же шара. Т.е. яблоко можно разрезать на 5 частей и собрать два яблока?! Посему и парадокс. Что еще интереснее, доказано, что если теория ZF непротиворечива, то добавив к ней аксиому выбора (ZF + Axiom of Choice = ZFC) мы получим непротиворечивую аксиоматику!
Искорка надежды
То мы что-то не можем доказать, то какие-то парадоксы. Может, математика — полная чушь? Может не следует ее изучать? Ответ: никакая не чушь, изучать следует. Почему же, спросит читатель. Я приведу достаточно физическое доказательство. Обычно в физике бывает так. «Ого, в течении 100 лет мы наблюдали за падением бутербродов и оказалось, что они падают маслом вниз, назовем это законом». Думаете, шучу? А попытайтесь доказать, что тела состоят из молекул. Ничего более строгого, чем то, что в течение 2000 лет эта теория не давала сбой, вы не придумаете. Так вот с математикой примерно та же ситуация. Мы используем ее, вроде бы машины едут, самолеты летят, здания стоят и все хорошо. Интуитивно ясно, что если бы в математике было противоречие, то, чем глубже бы мы копались в дебрях этой науки, тем легче бы были доказательства теорем, но такого не происходит.
И все же, откуда парадокс Банаха-Тарского возникает, все же достаточно логично! На самом деле, если аккуратно заметить, то во Вселенной нет ничего бесконечного. Нет ничего бесконечно малого и т.д. Просто удобно работать с бесконечными множествами. Так что вполне нормально, что могут получаться результаты не применимые к жизни.
Что такое аксиома, теорема, следствие
В данной публикации мы рассмотрим, что из себя представляют аксиомы, теоремы и следствия. Определения сопровождаются соответствующими примерами для лучшего понимания.
Что такое аксиома
Для того, чтобы решить многие математические задачи, очень часто требуется выполнить определенные логические действия, благодаря которым удается получить то или иное решение/доказательство.
Но есть в математике такие утверждения, которые не требуют никаких доказательств.
Например:
Эти и другие подобные утверждения, не нуждающиеся в доказательстве и принимаемые в качестве исходных в какой-либо теории, называются аксиомами (от древнегреческого “axioma”, что означает “положение”, “утверждение”). Иногда их еще называются постулатами.
Аксиомы могут использоваться для решения конкретных задач или применяться для доказательства теорем.
Примечание: не допускается искажение формулировок аксиом и большинства теорем, т.е. их нужно учить наизусть.
Что такое теорема
В отличие от аксиомы, теорема – это суждение, которе требуется доказать. Т.е. в рассматриваемой теории для нее есть определенное доказательство.
Например:
Есть отдельный вид так называемых вспомогательных теорем, которые сами по себе не полезны и используются только для доказательства других теорем. Их называются леммами (от древнегреческого “lemma”, что означает “предположение”).
Например:
Если произведение нескольких сомножителей делится на простое число p, то по крайней мере один из сомножителей делится на p (лемма Евклида).
Что такое следствие
Следствие – это утверждение, которое было выведено из аксиомы или теоремы. И оно, также, требуется доказательства.
Например:
Что такое аксиома, теорема и доказательство теоремы
Понятие аксиомы
Аксиома — это правило, которое считают верным и которое не нужно доказывать. В переводе с греческого «аксиома» значит принятое положение — то есть взяли и договорились, что это истина, с которой не поспоришь.
Аксиоматический метод — это подход к получению знаний, при котором сначала разрабатывают аксиомы, а потом с их помощью формулируют новые теории.
Синоним аксиомы — постулат. Антоним — гипотеза.
Основные аксиомы евклидовой геометрии
Учить наизусть эти аксиомы не обязательно. Главное — помнить о них и держать под рукой, чтобы при доказательстве теоремы сослаться на одну из них.
А теперь давайте рассмотрим несколько аксиом из геометрии за 7 и 8 класс.
Самая известная аксиома Евклида — аксиома о параллельных прямых. Звучит она так:
Это значит, что если дана прямая и любая точка, которая не лежит на этой прямой, то через неё можно провести только одну единственную прямую, которая будет параллельна этой первой данной прямой.
У этой аксиомы два следствия:
Аксиома Архимеда заключается в том, что, если отложить достаточное число раз меньший из двух отрезков, то можно покрыть больший из них. Звучит так:
Если на прямой есть меньший отрезок А и больший отрезок B, то, можно сложить А достаточное количество раз, чтобы покрыть B.
На картинке можно увидеть, как это выглядит:
Из этого следует, что не существует бесконечно малых и бесконечно больших величин. В качестве математической формулы аксиому можно записать так: А + А + … + А = А * n > В, где n — это натуральное число.
Понятие теоремы
Что такое аксиома мы уже поняли, теперь узнаем определение теоремы.
Теорема — логическое следствие аксиом. Это утверждение, которое основано на аксиомах и общепринятых утверждениях, которые были доказаны ранее, и доказывается на их основе.
Состав теоремы: условие и заключение или следствие.
Среди теорем выделяют такие, которые сами по себе не используются в решениях задач. Но их используют для доказательства других теорем.
Лемма — это вспомогательная теорема, с помощью которой доказываются другие теоремы. Пример леммы: если одна из двух параллельных прямых пересекает плоскость, то и вторая прямая тоже пересекает эту плоскость.
Следствие — утверждение, которое выводится из аксиомы или теоремы. Следствие, как и теорему, необходимо доказывать.
Примеры следствий из аксиомы о параллельности прямых:
Доказательство теоремы — это процесс обоснования истинности утверждения.
Каждая доказанная теорема служит основанием доказательства для следующей теоремы. Именно поэтому так важно изучать геометрию последовательно, переходя от аксиом к теоремам.
Способы доказательства геометрических теорем
Часть аналитического способа — доказательство от противного, когда для доказательства данного предложения убеждают в невозможности предположения противоположного.
Приемы для доказательства в геометрии:
Обратная теорема — это такой перевертыш: в ней условие исходной теоремы дано заключением, а заключение — условием.
Прямая и обратная теорема взаимно-обратные. Например:
В первой теореме данное условие — это равенство сторон треугольника, а заключение — равенство противолежащих углов. А во второй всё наоборот.
Противоположная теорема — это утверждение, в котором из отрицания условия вытекает отрицание заключения.
Вот, как выглядит взаимное отношение теорем на примере:
В геометрическом изложении достаточно доказать только две теоремы, тогда остальные справедливы без доказательства.
Записывайся на онлайн обучение по математике для учеников с 1 по 11 классы!
Доказательство через синтез
Рассмотрим пример синтетического способа доказательства.
Теорема: сумма углов треугольника равна двум прямым.
Дан треугольник: ABC. Нужно доказать, что A + B + C = 2d.
Доказательство:
Проведем прямую DE, так чтобы она была параллельна AC.
Сумма углов, лежащих по одну сторону прямой, равна двум прямым, следовательно, α + B + γ = 2d.
Так как α = A, γ = C, то заменим в предыдущем равенстве углы α и γ равными им углами: A + B + C = 2d. Что и требовалось доказать.
Здесь исходным предложением в цепи доказательств выбрана теорема о сумме углов, которые лежат по одну сторону прямой. Есть связь с теоремами о равенстве углов накрест-лежащих при пересечении двух параллельных третьею косвенною. Доказываемая теорема есть необходимое следствие всех предложенных теорем и является в цепи доказательств последним заключением.
Доказательство через анализ
Рассмотрим пример аналитического способа доказательства.
Теорема: диагонали параллелограмма пересекаются пополам.
Дан параллелограмм: ABCD.
Доказательство:
Если диагонали пересекаются пополам, то треугольники AOB и DOC равны.
Равенство же треугольников AOB и DOC вытекает из того, что AB = CD, как противоположные стороны параллелограмма и ∠α = ∠γ, ∠β = ∠δ, как накрест-лежащие углы.
Таким образом мы видим, что последовательно данное предложение заменяется другим и такое замещение совершается до тех пор, пока не дойдем до уже доказанного предложения.
Теоремы без доказательств
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
Доказательств может быть несколько. Одно из них звучит так: если построить квадраты на сторонах прямоугольного треугольника, то площадь большего из них равна сумме площадей меньших квадратов. На картинке понятно, как это работает:
Теорема косинусов: квадрат одной стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними. В виде формулы это выглядит так:
где a, b и c — стороны плоского треугольника,
α — угол напротив стороны а.
Следствия из теоремы косинусов:
Понятия свойств и признаков
У нас есть список аксиом и мы уже знаем, что такое теорема и как ее доказывать. Есть два типа утверждений среди теорем, которые часто встречаются при изучении новых фигур: свойства и признаки.
Свойства и признаки — понятия из обычной жизни, которые мы часто используем.
Свойство — такое утверждение, которое должно выполняться для данного типа объектов. У ноутбука есть клавиатура — это свойство есть у каждого ноутбука. А у электронной книги такого свойства нет.
Примеры геометрических свойств мы уже знаем: у квадрата все стороны равны. Это верно для любого квадрата, поэтому это — свойство.
Такое свойство можно встретить у другого четырехугольника. И клавиатура может быть на других устройствах, помимо ноутбука. Из этого следует, что свойства не обязательно должны быть уникальными.
Признак — это то, по чему мы однозначно распознаем объект.
Звезды в темном небе — признак того, что сейчас ночь. Если человек ходит с открытым зонтом — это признак того, что сейчас идет дождь. При этом ночью не обязательно должны быть видны звезды, иногда может быть облачно. Значит это не свойство ночи.
А теперь вернемся к геометрии и рассмотрим четырехугольник ABCD, в котором AB = BD = 10 см.
Является ли равенство диагоналей признаком прямоугольника? У такого четырехугольника, где AB = BD, диагонали равны, но он не является прямоугольником. Это свойство, но не его признак.
Но если в четырехугольнике противоположные стороны параллельны AB || DC и AD || BC и диагонали равны AB = BD, то это уже верный признак прямоугольника. Смотрите рисунок:
Иногда свойство и признак могут быть эквивалентны. Лужи — это верный признак дождя. У других природных явлений не бывает луж. Но если приходит дождь, то лужи на асфальте точно будут. Значит, лужи — это не только признак, но и свойство дождя.
Такие утверждения называют необходимым и достаточным признаком.
Аксиомы и постулаты Евклида в современном изложении
Данная статья относится к Категории: Построение научных теорий
«Совершенно ясное и строгое понимание дедуктивных схем пришло лишь в начале XX столетия. В основном это заслуга великого немецкого математика Гильберта. В несколько огрублённой и упрощённой форме дело обстоит примерно так. Мы ограничимся дальше, конкретным случаем геометрии, чтобы не слишком увлекаться абстракциями.
Этап № 1. Перечисление Основных Понятий.
Итак. Основные Понятия. Математики говорят прелестно: это элементарные объекты, которые не определяются, а лишь называются. Впрочем, маленькое добавление есть.
В современной аксиоматике геометрии Основные Понятия делятся на две группы:
б) Основные Соотношения.
Вообще говоря, сейчас есть по меньшей мере две существенно различные аксиоматические схемы. Дальше мы будем пользоваться той, в которой Основные Образы таковы:
Теперь посмотрим, что представляют собой Основные Соотношения. Они формулируются так:
Основные Понятия установлены. Теперь можно перейти ко второму этапу
Этап № 2. Основные Аксиомы.
Если строго придерживаться терминологии, введенной чуть ранее, надо было бы сказать так: двум различным точкам может принадлежать одна, и только одна, прямая. И далее в том же духе. Как хорошее упражнение рекомендую на основе этой аксиомы доказать теорему: «Две прямые имеют лишь одну общую точку».
Всего в евклидовой геометрии сейчас различают пять групп аксиом. Это:
1) аксиомы соединения;
3) аксиомы движения;
4) аксиома непрерывности;
5) аксиома о параллельных.
Вряд ли стоит сейчас перечислять все эти аксиомы, мы поместим их в приложении, памятуя слова Геродота, что ничто не придаёт книге такой вес и солидность, как приложения. К аксиомам мы ещё не раз вернёмся, а пока укажем.
Этап № 3. Перечисление Основных Определений.
Очевидно, мы должны были раньше дать определение этого понятия при помощи Основных. Это довольно легко можно сделать. Читатели могут проверить, насколько они прониклись духом дедукции, и, вооружившись списком аксиом, попытаться решить эту задачу.
Если бы оказалось, что, используя Основные Понятия, невозможно определить, что такое луч, тогда пришлось бы это понятие отнести к Основным.
В общем все остальные понятия и определения вводятся при помощи Основных, а также (внимание!) тех аксиом, которые установлены нами для Основных Понятий. Нам остался последний.
Этап № 4. формулировка теорем. Доказательство теорем.
Для наших понятий (Основных и неосновных) мы высказываем утверждения-теоремы, которые и доказываем. Это, собственно, и есть предмет геометрии. Я сейчас ещё раз хотел бы повторить, что в такой постановке геометрия превращается в совершенно абстрактную игру наподобие шашек либо, ещё лучше, шахмат.
Для решения этой «теоремы» игрок в ходе партии доказывает десятки лемм (вспомогательных теорем), выбирая всякий раз лучший, по его мнению, ход в данной позиции. Впрочем, отличие игр от геометрии есть. Оно состоит в том, что очень часто партнёрами принимаются неправильные «доказательства». В шахматах, скажем, не сформулированы (неизвестны) строгие логические критерии оценки каждого хода или позиции. В геометрии они есть. В ней всегда можно установить, что вновь сформулированная теорема противоречит предыдущим теоремам, а значит, противоречит и более ранним, а значит. Разматывая клубок до конца, мы приходим к двум возможностям.
Или мы допустили ошибку в нашем рассуждении, или теорема, которую мы вновь сформулировали, ошибочна.
Первая возможность малоинтересна для науки; она показывает лишь то, что мы плохо владеем математикой.
Зато во второй содержится определённый и часто очень важный результат. Если мы убедились, что наша гипотеза (теорема) неверна, следовательно, верны другие теоремы, именно те, что противоречат нашей. Если таких противоречащих теорем лишь одна, то вашим рассуждением мы её доказали.
Смилга В.П., В погоне за красотой, М., «Молодая гвардия», 1968 г., с. 32-36.
Изображения в статье
Евклид — древнегреческий математик, первый математик Александрийской школы / CC BY-SA 3.0
Image by Alexas_Fotos from Pixabay
Image by Med Ahabchane from Pixabay
Image by Vural Yavaş from Pixabay
двум различным точкам может принадлежать одна, и только одна, прямая.
Молдавские учёные решили проблему, над которой 140 лет бились математики всего мира
Два математика из Молдовы первыми в мире решили алгебраическую проблему, над которой 140 лет размышляли великие ученые мира. Об этом на этой неделе сообщил Технический университет Молдовы (UTM).
«Доктор физико-математических наук Михаил Попа и доктор математических наук Виктор Прикоп первыми в мире нашли решение знаменитой проблемы центра и фокуса, поставленной выдающимся французским математиком Анри Пуанкаре, над которой великие математики мира размышляли более века», — говорится на сайте университета.
Этой проблеме посвятили тысячи работ математики из Франции, России, Беларуссии, Китая, Великобритании, Канады, США и других стран мира. Только в Молдове число работ, посвященных проблеме Пуанкаре, приближается к сотне, отметили в UTM.
Профессор университета Михаил Попа, основатель научной школы алгебры Ли и дифференциальных систем, предложил собственное решение проблемы центра и фокуса, которое привело его к результату, ставшему открытием.
Во время исследований к профессору присоединился его ученик Виктор Прикоп. Вместе они усовершенствовали первоначальную гипотезу в монографии «Проблема центра и фокуса. Алгебраические решения и гипотезы».
Работа была переведена на английский язык и представлена для издания в несколько зарубежных издательств. В итоге лучшие условия предложил издательский дом «Taylor & Francis Group», расположенный в Великобритании и специализирующийся на публикациях научной литературы и журналов.
Где-то всплакнул Гриша Перельман.
Панорама, да не та. И с такими лицами не шутят.
Что такое наука и какие задачи она должна решать? Существует ли музыкальная наука и какими могут быть результаты применения научного метода в этой сфере? Что такое микрохроматика и как она может изменить музыку будущего, расширить возможности её создания и восприятия?
Как древние греки вычислили длину окружности Земли
Коротко и наглядно о том, как древнегреческий математик и астроном Эратосфен Киренский вычислил размеры Земли ещё в III веке до нашей эры.
Реставрирую шкаф
Работа не быстрая, поэтому фото до. Нашел в нем тайник, в тайнике фото.
Интересует, что за формула на доске?
Пока ответа не нашлось.
Шкаф в СПБ. Ещё была найдена карта Казани печать старая начало 20 века.
Школьники не смогли решить заданную Мишустиным задачу
1 сентября 2021, 13:04Текст: Алексей Дегтярев
Премьер-министр Михаил Мишустин в ходе визита в физтех-лицей имени Капицы на День знаний на уроке одиннадцатиклассников задал им физтеховскую задачу.
Глава правительства вошел в класс с букетом цветов, он вручил их преподавателю математики Ольге Браславской, ученики в этот момент решали задачу по анализу бизнес-проектов, передает РИА «Новости».
«Зачем же в физтехе бизнес-проектами заниматься, ребята? Здесь нужны фундаментальные знания, правильно?», – обратился к учащимся премьер.
«В современное время нужны специалисты на все руки, особенно в России», – ответили ученики.
Мишустин на доске начертил задачу для школьников, он предложил провести перпендикуляр от точки окружности к диаметру, не используя никаких измерительных приборов, и дал время на ее решение, сообщив, что зайдет позднее.
Школьники начали бурно обсуждать задачку и искать ответ, но не смогли справиться с ней.
Мишустин вернулся в класс и раскрыл решение задачи, подкрепив его ответом на доске.
«Конечно, очень важно решать задачи, связанные с бизнесом, и с приложением математических фундаментальных знаний, которыми вы обладаете. Но мне кажется, в вашем возрасте хорошо бы фундаменталки поднабраться. А когда вы будете обладать математическими знаниями, физикой, химией, вы сможете решать любые задачи, включая бизнес», – сказал премьер.
Напомним, Мишустин в День знаний посетил физтех-лицей имени Капицы, который находится в подмосковном Долгопрудном. Обучение в вузе ведется с 5 по 12 классы. С 2015 по 2021 годы лицей выпустил 94 медалиста, 85 победителей и призеров заключительного этапа Всероссийской олимпиады школьников, 45 победителей и призеров международных олимпиад.
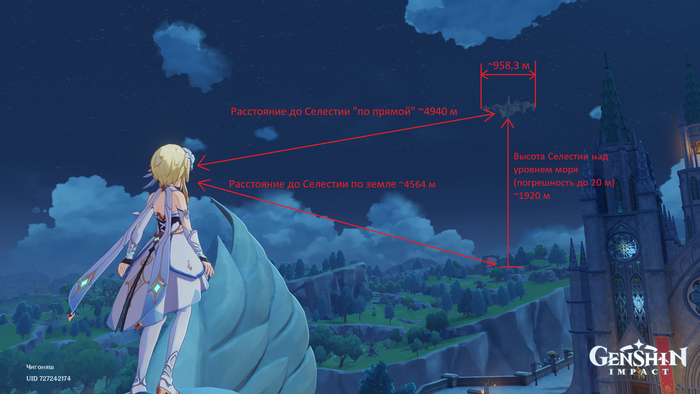
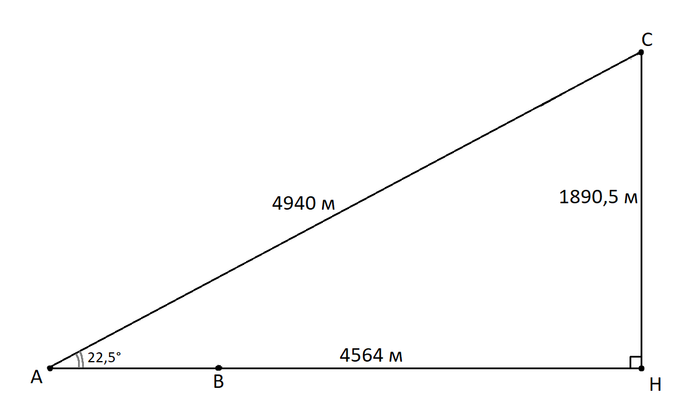
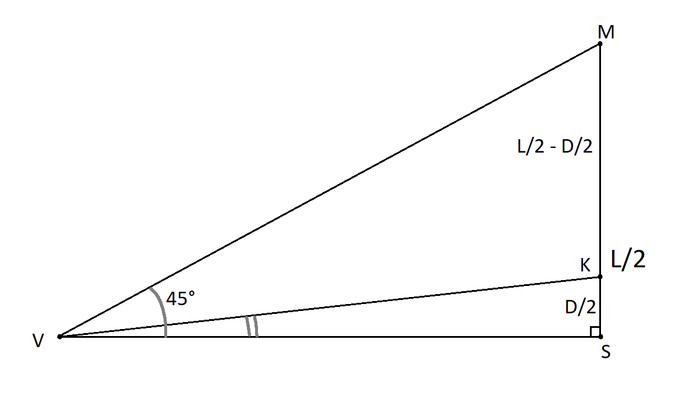
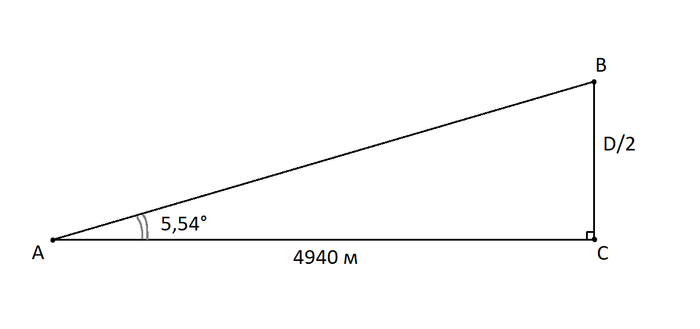
Каких размеров Селестия и как далеко она находится | Genshin Impact
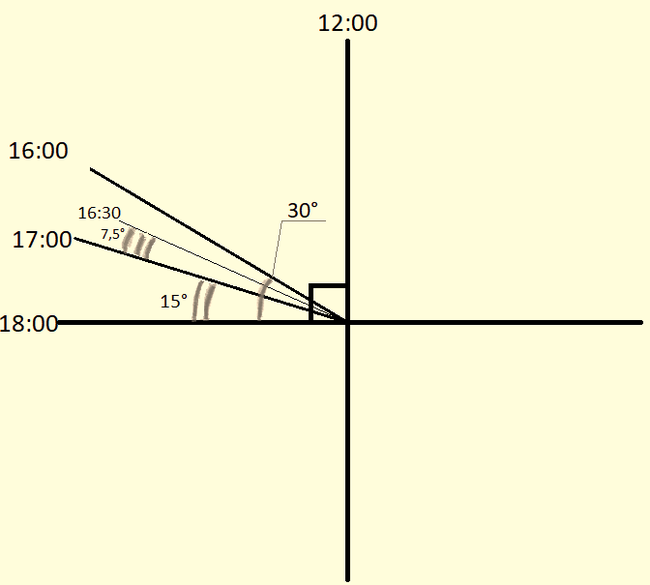
Еще можно измерить угловой размер Селестии, но об это позже
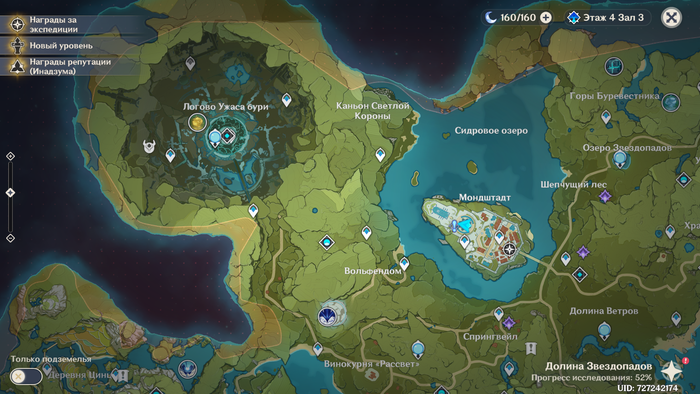
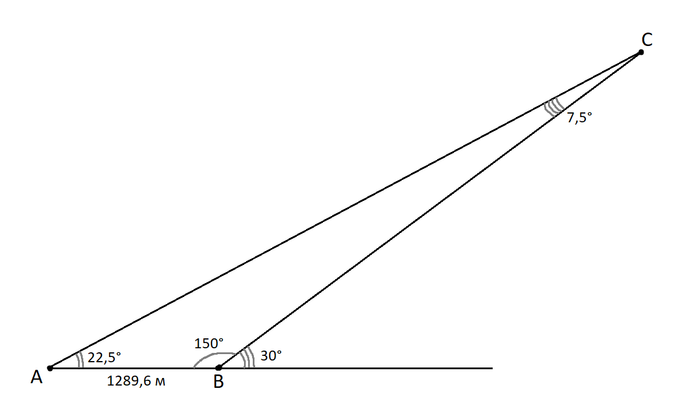
И так, у нас есть необходимые данные: расстояние между точками замера 1289,6 м, угол над горизонтом в Монштадте
22,5°, возле логова Ужаса Бури
Что, если наш 4D мир станет пятимерным?
Краткая текстовая версия видео:
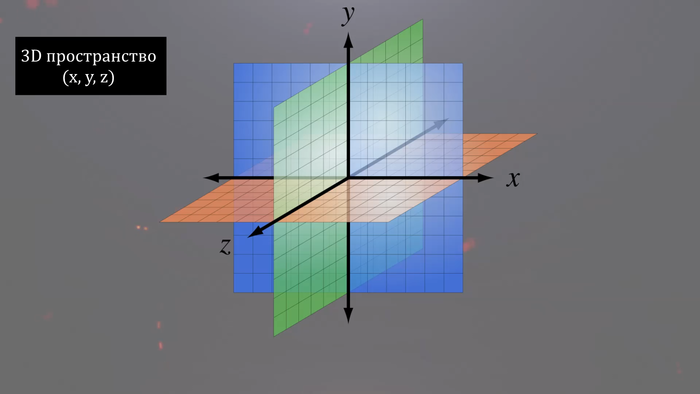
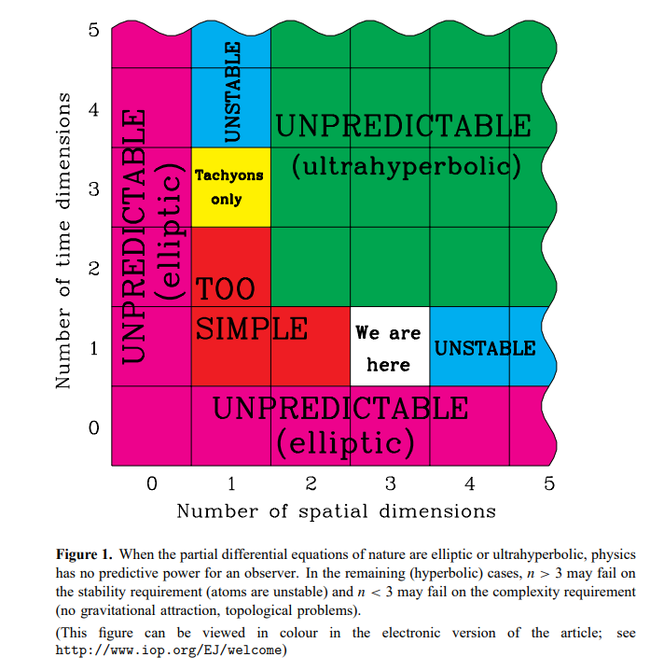
Мир, в котором мы живем, является четырехмерным. По крайней мере в макро масштабе. В нашем мире 3 пространственных измерения и одно временное. Трехмерность пространства значит, например, то, что мы можем в нем провести три взаимно перпендикулярных координатных осей расположенных под углом 90 градусов. В таком пространстве можно двигаться «влево-вправо», «вперед-назад» и «вверх-вниз».
В трехмерном пространстве мы можем завязать узел. В двумерном пространстве завязать узел невозможно. А еще в трехмерном пространстве стул может стоять только на трех ножках или больше, стул на двух ножках потеряет равновесие и упадет (Речь идет о ножках типа такого, как на фото).
А что будет, если мы добавим еще одно пространственное измерение? То есть представим себе пятимерный мир, 4 пространственных измерения и 1 временное?
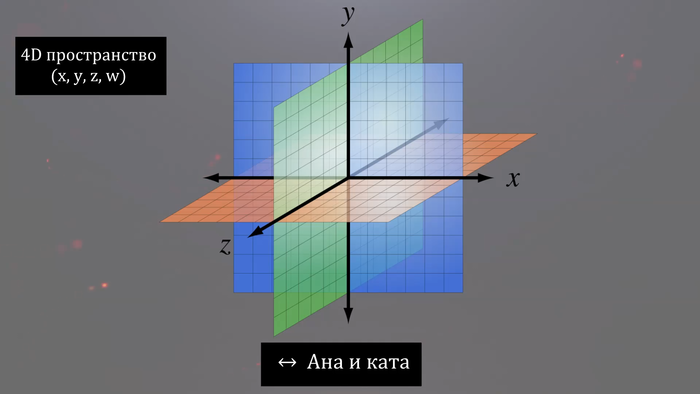
В таком мире можно провести еще одну ось перпендикулярную к остальным трем осям под углом 90 градусов. В трехмерном пространстве сделать это невозможно и как-то точно визуализировать я это не могу, так что включайте фантазию.
В пятимерном мире так же добавятся новые направления движения, которые называют «ана-ката», получается: «влево-вправо», «вперед-назад», «вверх-вниз» и «ана»-«ката». Представить себе направление движения ана и ката мы не можем, так же как существо в двумерном мире не может представить себе направления вверх и вниз.
В таком мире можно завязать двумерную сферу на узел, в нашем мире сделать это невозможно, показать, соответственно, тоже нельзя. Ну и стул с тремя ножками не сможет стоять в мире с 4 пространственными измерениями, чтобы он был устойчив потребуется 4 или больше ножек.
Ну хорошо, я понимаю, вы вряд ли Вы читаете это, чтобы узнать о узлах и ножках стула, Вас интересует, что будет с нашим миром, если внезапно в него добавить еще одно измерение, вот так по щелчку пальца «тыц» и добавили еще одно пространственное измерение и вот ты уже в 5 измерении, что с тобой будет?
Если коротко то… умрешь конечно же. А еще Земля станет приплюснутой. Сейчас расскажу как именно умрешь и почему земля станет приплюснутой.
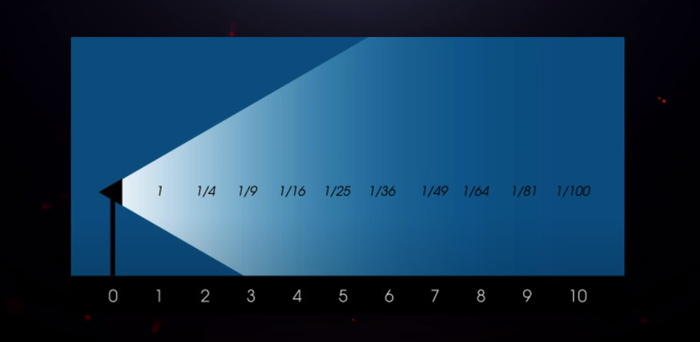
Есть такой закон – закон обратных квадратов, и он тесно связан с размерностью пространства. Возьмем для примера светящий фонарь, интенсивность света в таком случае убывает согласно закону обратных квадратов.
Объект, перемещенный на расстояние в 2 раза большее от источника, получает только четверть той мощности, которую он получал в первоначальном положении. На расстоянии в 3 раза большее от источника – в 9 раз меньше мощности, на расстоянии в 4 раза большее от источника – 16 раз и так далее.
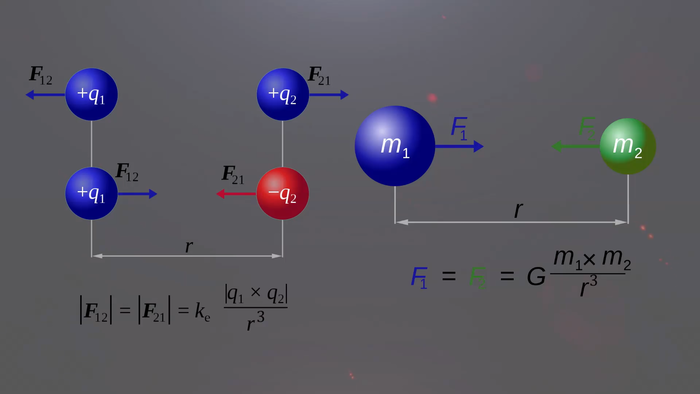
В законе всемирного тяготения сила гравитационного притяжения убывает тоже с квадратом расстояния. В два раза увеличиваем расстояние, сила притяжения уменьшается в 4 раза и так далее. Тоже самое с законом Кулона – сила притяжения или отталкивания заряженных частиц убывает с квадратом расстояния. В 5D мире закон обратных квадратов превращается в закон обратных кубов. Теперь интенсивность света будет падать не с квадратом расстояния, а с кубом расстояния. r^2 в законе Кулона и Законе всемирного тяготения превращается в r^3.
Это все полностью изменит химические элементы из которых мы состоим, некоторые атомы станут нестабильными, радиоактивными, другие наоборот, станут стабильными.
Например, в 5D мире магний был бы благородным газом, а не металлом, то есть некоторые элементы станут менее реактивными, другие более реактивными. Ионизация атомов будет осуществляться при значительно меньших энергиях, да и вообще агрегатное состояние различных элементов будет меняться не так, как в нашем мире, некоторые хим. элементы станут газообразны при комнатной температуре, некоторые затвердеют и такие вот вещи. Думаю, практически бессмысленно вспоминать биологические процессы, благодаря которым мы можем жить, ведь это все поменяется кардинально, мы мгновенно потеряем сознание и умрем, синтез белков, транспортировка различных аминокислот, нейромедиаторов, нервные импульсы, это все либо прекратится, либо изменится до неузнаваемости. Ну и конечно же спектры атомов изменятся, а это значит, что все резко поменяет цвет, что-то станет прозрачным, что-то непрозрачным, да и вообще привычные для нас источники света выглядели бы более тускло из-за r^3, с запахами та же история, правда уже некому будет смотреть и нюхать все это, ведь все живые существа погибнут.
Короче будет происходить полная жесть, что-то будет плавится, что-то превратится в газ, что-то затвердеет, некоторые вещества станут радиоактивными, привычные нам вещи потеряют свои свойства и перестанут работать так, как в нашем мире. Я напомню, что это все в мире, в котором 4 пространственных измерения и одно временное и в котором можно двигаться в направлении ана и ката. Но кроме дополнительного направления появятся также дополнительные степени свободы во вращении. В нашем мире ориентацию тела можно задать тремя углами, в быту это называется «наклон, подъём и поворот», в 5D мире надо представить себе еще 3 дополнительных степени свободы вращения перпендикулярные к 3 вышеупомянутым. Но по идее, на вращение Земли это не должно повлиять, момент импульса сохранится, ведь нужно, чтобы какая-то сила передала момент импульса Земле, чтобы она могла вращаться в какой-то непривычный для нас способ. Конечно Земля изменит свой привычный облик, из-за того, что свойства химических элементов изменятся, но из-за гравитации все должно также удерживаться вокруг центра масс, правда земля довольно быстро вращается, а так как гравитация в 5D мире у нас ослабевает с кубом расстояния, то земля сплюснется и формой будет напоминать что-то типа такого, как на картинке.
Но вообще, появится дополнительное направление, в котором могут двигаться частицы из которых состоит земля, планета начнет превращаться в гиперсферу, представить себе этот процесс, эти метаморфозы которые будут происходить, очень сложно.
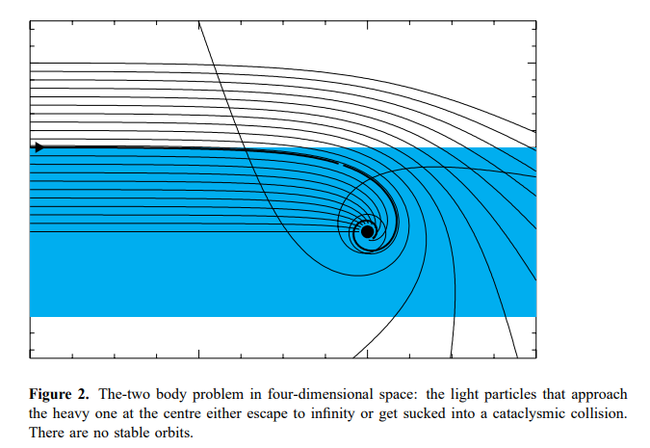
Будут ли происходить термоядерные реакции на солнце, тут под вопросом, но изменения явно произойдут. Но вот что забавно – в пятимерном мире нет стабильных орбит. Вот, посмотрите на график, это моделирование классической задачи двух тел, оказывается, что устойчивых орбит в 5D мире нет, тела либо падают друг на друга, либо улетают в бесконечность, поэтому солнечная система, как и все другие системы, разрушится, некоторые тела упадут на другие тела, а некоторые улетят бороздить просторы галактики.
Казалось бы, следуя логике как с законом обратных квадратов, все квадраты в других уравнениях тоже надо заменить на кубы и получается, что формула эквивалентности массы и энергии в пятимерном пространстве будет работать как Е=мс в кубе, но нет, эта формула, как и множество других, не изменятся в пятимерном пространстве, она, как и множество других формул, не зависит от размерности пространства.
Но даже и без этого всего, мир в 5 мерном пространстве изменится настолько, что в нем не сможет существовать жизнь в том виде, в котором существует в четырехмерном пространстве. Вообще, оказывается, четырехмерный мир – самый простой из возможных и одновременно самый оптимальный для существования в нем жизни, стабильных орбит и химии, какой мы ее знаем.
Книга Кипа Торна, «Интерстеллар. Наука за кадром»
Единственный в своём роде треугольник Шарыгина, открытый лишь в 1982 году
Приветствую Вас, уважаемые Читатели! Сегодня я хочу рассказать об удивительном геометрическом объекте, впервые рассмотренным советским математиком Игорем Федоровичем Шарыгиным.
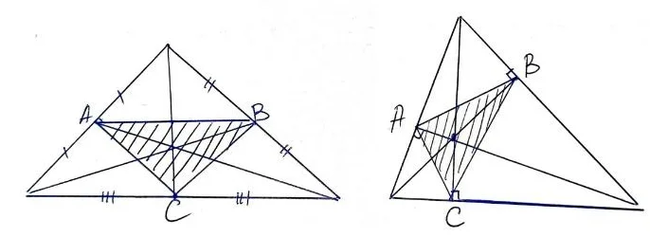
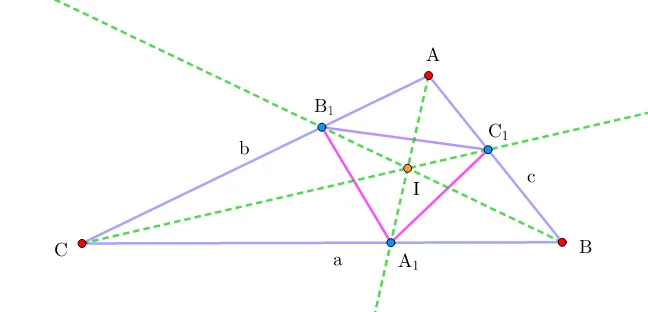
Для начала посмотрите на рисунок ниже. Что Вы на нём видите?
Но, погодите, есть же еще биссектрисы!
И тут становится интересно! Оказывается, и это показал Игорь Федорович, полученный из биссектрис треугольник может быть равнобедренным!
Заметка Шарыгина об этом объекте опубликована в книге «Задачи по геометрии. Планиметрия», 1982.
Впрочем, есть одно очень тонкое условие: угол такого треугольника должен попадать в диапазон от 102,663 до 104,478 градусов!
Основная суть доказательства сводится к рассмотрению подобных треугольников и применению теоремы косинусов, что позволяет получить вот такие выражения для сторон треугольника:
Самим доказательством (доступным каждому школьнику 9 класса!) можно проникнуться в телеграмм-канале «Математика не для всех».
Ответ на пост «Гифка с фурами нервно курит в сторонке»
Больше фракталов богу комплексных чисел!
Математика
Псковский математик, разработавший способ моментально вычислять коррупционеров по декларациям, останется в СИЗО до суда
В Пскове один из районных судов постановил оставить в силе меру пресечения в виде заключения под стражу для местного математика Дмитрия Теплова. 57-летний мужчина был задержан после того, как представил в сети программно-математический алгоритм, позволяющий автоматически и с высокой долей вероятности вычислять чиновников по их налоговым декларациям.
Учёный утверждал, что психология среднестатистического коррупционера легко поддаётся изучению. Все они не умеют остановиться и стремятся украсть ещё больше и больше с каждым годом, причём как минимум часть подобных денег приходится отражать в декларациях, “легализовывая” их через бизнес, чтобы они хотя бы отдалённо соответствовали реальной картине и не вызывали подозрений. Рано или поздно каждый из них попадается на “очевидно нетрудовых сверхдоходах”, которые несложно описать математическими алгоритмами.
Теплов опубликовал в сети методы таких вычислений и продемонстрировал их высокую работоспособность – автоматизированный анализ деклараций уже осужденных коррупционеров давал результаты порядка 92-99%, причём аналогичная вероятность оказаться коррупционером была найдена у множества действующих чиновников. Вскоре исследователя задержали по обвинению в клевете на представителей органов власти и экстремизме.
Согласно очередному решению суда, учёный будет находиться под арестом, как подозреваемый, представляющий собой высокую опасность. В июне должен состояться суд, на котором будут рассмотрены обвинения против математика в разжигании ненависти к социальной группе “государственные служащие”, а также о клевете в отношении лиц из регионального и федерального правительств.
От просветительской деятельности освободят музеи и библиотеки
Минпросвещения доработает ведомственное положение, которое регулирует условия осуществления просветительской деятельности в России. Речь идет о подзаконном акте к одноименному закону, который подвергся критике представителей научного, образовательного и культурного сообществ. Документ обязывает школы, вузы и музеи заключать договоры со сторонними лекторами даже для разового мероприятия, а иностранным агентам и вовсе запрещает подобное сотрудничество. В Минпросвещения не исключили, что от регулирующего действия документа освободят учреждения культуры. В ведомстве также анонсировали второй подзаконный акт к закону о просветительской деятельности — им планируется урегулировать международное сотрудничество школ и вузов.
Слушания в четверг в Общественной палате были посвящены обсуждению двух, может быть, самых резонансных документов последних лет — закона о просветительской деятельности и проекта подзаконного акта к нему. Закон был раскритикован представителями научного, образовательного и культурного сообществ за само определение «просветительской деятельности»: к ней можно отнести практически каждого, кто делится информацией «вне рамок образовательных программ». Подготовленное же Минпросвещения постановление правительства РФ «Об утверждении положения об осуществлении просветительской деятельности» уточняет темы такой деятельности, а также формы, в которых она может осуществляться (см. “Ъ” от 26 апреля).
Минпросвещения фактически приравнивает просветителей к штатным преподавателям: у них не должно быть ограничений для педагогической работы, установленных ст. 331 Трудового кодекса (ТК РФ).
В частности, сторонний лектор обязан иметь среднее профессиональное или высшее образование и не быть судимым за преступления против основ конституционного строя, безопасности государства и общественной безопасности. Он также должен не менее двух лет заниматься просветительством или участвовать «в реализации общественно значимых инициатив». Дополнительное ограничение установлено в проекте правительственного постановления для юридических лиц: помимо отсутствия задолженностей по налогам и сборам они не должны быть включены в реестр НКО—иностранных агентов.
«Логика законодателей понятна — она связана с темой иноагентов, темой влияния на образовательную сферу определенных сил, которых законодателям не хотелось бы наблюдать в России,— объяснил смысл документов глава президентского Совета по правам человека Валерий Фадеев.— Есть и примеры: несколько лет назад в Бундестаге выступил подросток, вызвав жесткую общественную реакцию в России (в 2017 году школьник из Нового Уренгоя, выступая в Бундестаге, заявил, что многие немцы во времена Второй мировой войны «хотели жить мирно и не желали воевать». Эти слова вызвали в России скандал.— “Ъ”). Его же кто-то научил тому, что он там произнес?»
Однако статс-секретарь, замминистра просвещения Андрей Корнеев не пояснил, почему ведомство решило оградить школы, вузы, научные организации и учреждений культуры от иноагентов. «Может, вся наша дискуссия происходит из-за неправильного толкования? — предположил он.— (В законе о просветительской деятельности— “Ъ”) нет регулирования просветительства в сети интернет, регулирования в СМИ, нет положений, касающихся какого-либо реестра просветителей, нет положений, которые касаются государственного контроля».
Господин Корнеев также обратил внимание, что подзаконный акт, разработанный ведомством, регулирует только, «как образовательные, научные организации, организации в сфере культуры на своей инфраструктуре для школьников и студентов должны провести мероприятия просветительской направленности».
«Вся деятельность на территории организации должна иметь юридическое направление,— заявил он.— Чтобы родители обучающихся и сами обучающиеся знали, какие у них есть права, какие права есть у лица, которое приглашают, какие обязанности и какая ответственность». При этом замминистра не согласился с толкованием формулировки в разработанном ведомством документе: «Все посчитали: чтобы мне осуществить просветительскую деятельность вне организации, мне нужно искать образовательную организацию, чтобы заключить договор. Конечно нет. Здесь не идет об этом речь».
Замсекретаря ОП РФ Владислав Гриб поинтересовался, может ли ветеран войны прийти в школу и прочесть лекцию или придется собирать справки и заключать договор? «Рассказ о своей биографии под понятие о просветительской деятельности не попадает, поэтому может»,— ответил Андрей Корнеев.
Однако из зала чиновнику возразили, указав на положение в ведомственном документе, под которое подпадает биография ветерана: «распространение духовно-нравственных ценностей народов Российской Федерации, исторических и национально-культурных традиций». На это господин Корнеев возразить не смог.
«В субботу участвовал в «Библионочи»: собираются в местной библиотеке жители, им рассказывают про книжки. Естественно, это делают бесплатно, никакого договора не подписывают. Если бы мне сказали, что нужен договор, нужна справка о налогах…»,— сказал Григорий Тарасевич и махнул рукой. «Пишет мне школа на Сахалине: не прочтете ли нам лекцию? — привел схожий пример астрофизик, ведущий научный сотрудник ГАИШ МГУ Сергей Попов (автор петиции с требованием не принимать поправки о просветительской деятельности, собравшей около 250 тыс. подписей).— Я говорю: да, конечно, прочту, давайте подберем время. Если бы мне они сказали (подписать.— “Ъ”) договор с подписью в оригинале, который должен попасть на Сахалин, я бы просто сказал: «Забудьте об этом»». «Учитывая масштабы просветительской деятельности, мы этой отчетностью вас засыплем»,— пригрозил чиновникам Григорий Тарасевич.
Политолог Екатерина Шульман заявила, что нововведение приведет к созданию «рынка фальшивых справок и разрешений»: Неизвестно, кто должен выдавать подтверждение, что лектор имеет двухлетний опыт работы в этой деятельности. За то, чтобы договориться с площадкой, чтобы вас пустили туда прочитать лекцию, тоже можно представить, что можно будет дать взятку».
«То, чем мы занимаемся,— это бесконечная просветительская деятельность,— заметила режиссер, президент фонда содействия решению проблем аутизма в России «Выход» Авдотья Смирнова.— Мы проводим конференции международные, привозим международных специалистов, и я хожу в школы, где появился класс с детьми с аутизмом. Проект постановления приводит к тому, что благотворительный фонд «Выход» надо закрывать. Вы живете в волшебном мире розовых пони, Сороса, иностранных агентов и страшных козней, направленных на нашу страну. А я живу в мире, в котором учителя считают, что ребенок орет, потому что плохо воспитан, а не потому, что у него аутизм».
«Если мне не ответят на мои вопросы внятно, я закрою фонд, и в России не будет больше системной организации, которая занимается этой проблемой»,— предупредила госпожа Смирнова.
«Какие у вас взаимоотношения с руководством школы? — поинтересовался Андрей Корнеев.— Вы просто стучите в дверь? Приходите: «Пустите меня, я прочитаю лекцию»? У вас все равно есть какие-то документы».
В качестве примера госпожа Смирнова привела «Уроки добра», в рамках которых благотворительные организации приходят в школу с лекциями без заключения договоров.
«То, что говорит Авдотья Смирнова,— это акция под эгидой Минпросвещения, там есть все юридические документы,— парировал господин Корнеев.— Если существует программа или акция, которые утвердил Минпросвещения, то участники акции не должны заключать договор».
«Десятки и сотни тысяч просветительских мероприятий в виде лекториев, онлайн лекториев, конференций авторских экскурсий, которые проводятся не сотрудниками музея, подпадают под действие закона и постановления,— заявил вице-президент ИКОМ (Российский комитет Международного совета музеев) Сергей Богатырев.— Это приведет к тому, что из сотен тысяч мероприятий мы в статистке получим сотни. Не будут научные, музейные сотрудники заключать договоры, чтобы мы собрались и провели научную конференцию».
Андрей Корнеев напомнил, что Минкультуры просило к второму чтению вывести учреждения культуры из-под действия закона, но это предложение в Госдуме отклонили. «Мы позицию Минкультуры не получили на постановление, чувствую, она будет такой, как вы только что и сказали,— продолжил господин Корнеев.— Мы с коллегами проговорим, не исключено, что культура из постановления исключится». Отметим, с просьбой исключить работу воскресных школ из-под действия закона о просветительской деятельности в четверг выступили и представители Русской православной церкви.
Господин Корнеев также анонсировал, что после майских министерство представит для общественного обсуждения второй подзаконный акт, который позволит запустить закон о просветительской деятельности. Речь идет о порядке подписания Минпрсвещения и Минобрнауки заключений на международные договоры образовательных организаций.