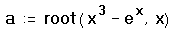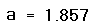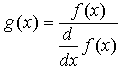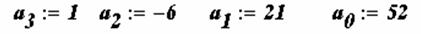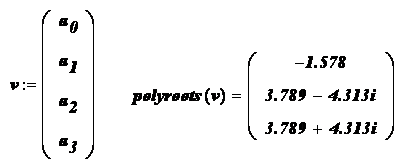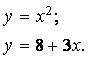что такое root в маткаде

Что такое root в маткаде

Глава 4. Решение уравнений

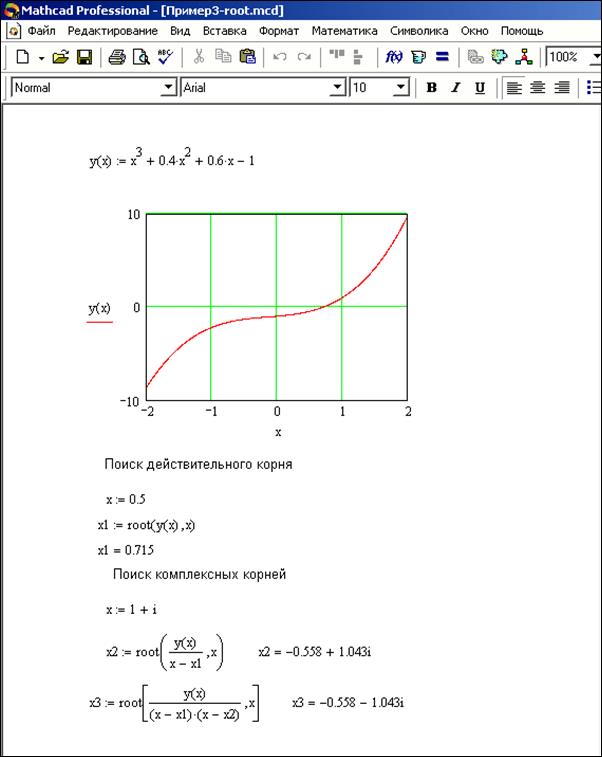
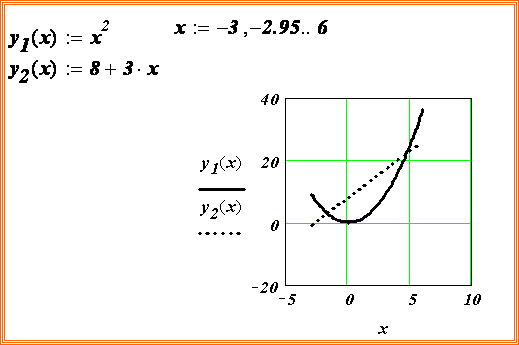
Функция root используется для решения одного уравнения с одним неизвестным. Перед началом решения желательно построить график функции, чтобы проверить, есть ли корни, то есть пересекает ли график ось абсцисс. Начальное приближение лучше всего выбрать по графику поближе к корню, так как итерационные методы весьма чувствительны к выбору начального приближения.

Обращение к функции осуществляется следующим образом:

root ( f ( x ), x ), где f ( x ) – выражение, равное нулю; x – аргумент, варьируя который, система ищет значение, обращающее в нуль ( рис. 4.1 ).

Уравнение

начальное приближение

решение

или

другие корни

Задан интервал поиска корней

Рис. 4. 1 Использование функции root

Mathcad позволяет вместо начального приближения задавать диапазон значений аргумента, в котором лежит значение искомого корня. В этом случае обращение к функции root должно иметь четыре параметра:

где a и b – границы интервала, в котором лежит один корень уравнения. Внутри интервала не должно быть больше одного корня, так как Mathcad выводит на экран лишь один корень, лежащий внутри интервала.

Значение функции на границах интервала должно быть разного знака, иначе, возможно, корень не будет найден.

Если функция имеет мнимый корень,

то начальное приближение задается комплексным числом

— начальное приближение

Рис. 4. 2 Решение уравнения с комплексными корнями

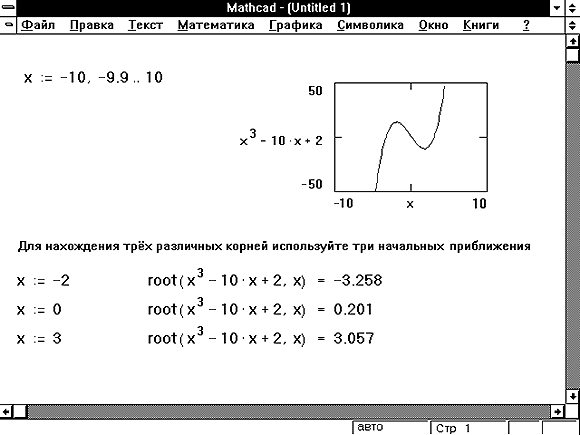
Если уравнение имеет несколько корней, то для их нахождения можно использовать разложение функции f ( x ) на простые множители:

,

где ,

и т. д. (рис. 4.3)

у этой функции 3 корня

диапазон значений х для вывода графика

Рис. 4. 3 Определение трех корней уравнения

1) в стандартном меню Mathcad выберите команду Tools → Worksheet Options → Built – In Variables (Инструменты → Параметры документов → Встроенные переменные);

2) в открывшемся окне поменяйте значение Convergence Tolerance ( TOL ) (Погрешность сходимости).

Для повышения точности расчета корня можно заменить f ( x ) на

.

Корень можно найти и по графику, увеличив масштаб. Для этого необходимо:

1) выделить график, щелкнув левой кнопкой мыши внутри графика;

2)в главном меню Mathcad выбрать команду Format → Graph → Zoom (Формат→График→Масштаб);

3) при нажатии левой кнопки мыши обвести пунктирной линией область графика вблизи искомого корня, которую надо увеличить;

Прямо с графика можно передать в буфер обмена численное значение корня. Для этого выполните следующие действия:

1) Выделите график, щелкнув левой кнопкой мыши внутри графика,

2) в главном меню Mathcad выберите команду Format → Graph → Trace (Формат→График→Трассировка),

3) щелкните левой кнопкой мыши внутри графика – появится перекрестье осей,

4) двигая мышь при нажатой левой кнопке, установите перекрестье на пересечении графика с осью абсцисс. При этом численные значения координат перекрестья появляются в открытом окне X – Y Trace (Трассировка X и Y ).

5) правильно выбрав положение перекрестья, нажмите кнопки Copy X и Copy Y – численные значения будут помещены в буфер

6) вне поля графика запишите имя, которое хотите дать корню, и оператор присваивания :=. Нажмите кнопку Paste (Вставить) в стандартном меню Mathcad или в контекстном меню, открывающемся при нажатии правой кнопки мыши.

Рис. 4. 4 Определение корня уравнения по графику

В окне X – Y Trace есть пункт Track Data Points (Отмечать расчетные точки). Если установить этот флажок, при перемещении мыши пунктирное перекрестье на графике будет перемещаться скачками, отмечая расчетные значения функции. Если флажок снять, движение перекрестья становится плавным.

Источник

Что такое root в маткаде

Для решения одного уравнения с одним неизвестным используется функция root. Аргументами этой функции являются выражение и переменная, входящая в выражение. Ищется значение переменной, при котором выражение обращается в ноль. Функция возвращает значение переменной, которое обращает выражение в ноль.

Первый аргумент есть либо функция, определенная где-либо в рабочем документе, или выражение. Выражение должно возвращать скалярные значения.

Второй аргумент — имя переменной, которое используется в выражении. Это та переменная, варьируя которую Mathcad будет пытаться обратить выражение в ноль. Этой переменной перед использованием функции root необходимо присвоить числовое значение. Mathcad использует его как начальное приближение при поиске корня.

Функция root предназначена для решения одного уравнения с одним неизвестным. Для решения систем уравнений используйте методику, описанную в следующем разделе “Системы уравнений”. Для символьного решения уравнений или нахождения точного численного решения уравнения в терминах элементарных функций выберите Решить относительно переменной из меню Символика. См. Главу “Символьные вычисления”.

Рисунок 1: Использование графика и функции root для поиска корней уравнения.

Что делать, когда функция root не сходится

Mathcad в функции root использует для поиска корня метод секущей. Начальное значение, присвоенное переменной x, становится первым приближением к искомому корню. Когда значение выражения f(x) при очередном приближении становится меньше значения встроенной переменной TOL, корень считается найденным, и функция root возвращает результат.

Чтобы установить причину ошибки, исследуйте график f(x). Он поможет выяснить наличие корней уравнения f(x)=0 и, если они есть, то определить приблизительно их значения. Чем точнее выбрано начальное приближение корня, тем быстрее функция root будет сходиться к точному значению. roots;using plots to find

Некоторые советы по использованию функции root

Решение уравнений с параметром

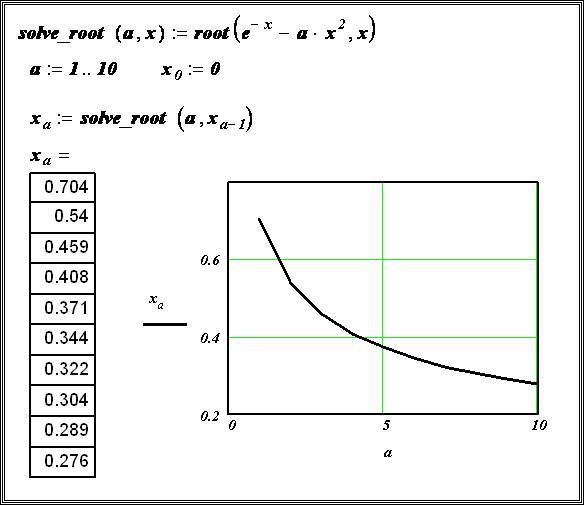
Предположим, что нужно решать уравнение многократно при изменении одного из параметров этого уравнения. Например, пусть требуется решить уравнение для нескольких различных значений параметра a. Самый простой способ состоит в определении функции

Чтобы решить уравнение для конкретного значения параметра a, присвойте значение параметру a и начальное значение переменной x как аргументам этой функции. Затем найдите искомое значение корня, вводя выражение f(a,x)=.

Рисунок 2 показывает пример того, как такая функция может использоваться для нахождения корней исследуемого уравнения при различных значениях параметра. Обратите внимание, что, хотя начальное значение x непосредственно входит в определение функции, нет необходимости определять его в другом месте рабочего документа.

Рисунок 2: Определение функции пользователя с функцией root.

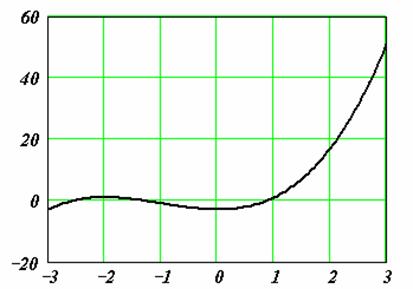
Нахождение корней полинома

Для нахождения корней выражения, имеющего вид

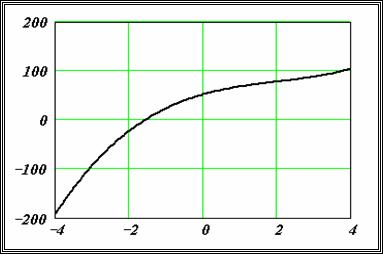
лучше использовать функцию polyroots, нежели root. В отличие от функции root, функция polyroots не требует начального приближения. Кроме того, функция polyroots возвращает сразу все корни, как вещественные, так и комплексные. На Рисунках 3 и 4 приведены примеры использования функции polyroots.

Функция polyroots всегда возвращает значения корней полинома, найденные численно. Чтобы находить корни символьно, используйте команду Решить относительно переменной из меню Символика. См. Главу “Символьные вычисления”.

Рисунок 3: Использование функции polyroots для решения задачи, изображенной на Рисунке 1.

Рисунок 4: Использование функции polyroots для поиска корней полинома.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Источник

Что такое root в маткаде

8.1. Одно уравнение с одним неизвестным

Рассмотрим одно алгебраическое уравнение с одним неизвестным х.

Для решения таких уравнений Mathcad имеет встроенную функцию root, которая, в зависимости от типа задачи, может включать либо два, либо четыре аргумента и, соответственно, работает несколько по-разному.

Первый тип функции root требует дополнительного задания начального значения (guess value) переменной х. Для этого нужно просто предварительно присвоить х некоторое число. Поиск корня будет производиться вблизи этого числа. Таким образом, присвоение начального значения требует априорной информации о примерной локализации корня.

Приведем пример решения очень простого уравнения sin(x)=o, корни которого известны заранее.

Листинг 8.1. Поиск корня нелинейного алгебраического уравнения

Рис. 8.1. Графическое решение уравнения sin(x)=0

График функции f (x)=sin(x) и положение найденного корня показаны на рис. 8.1. Обратите внимание, что, хотя уравнение имеет бесконечное количество корней xn=npi (n=0,±1,±2. ), Mathcad находит (с заданной точностью) только один из них, х0, лежащий наиболее близко к х=0.5. Если задать другое начальное значение, например х=3, то решением будет другой корень уравнения х1=pi и т. д. Таким образом, для поиска корня средствами Mathcad требуется его предварительная локализация. Это связано с особенностями выбранного численного метода, который называется методом секущих и состоит в следующем (рис. 8.2):

Листинг 8.3. Поиск мнимого корня

Для решения этого уравнения второй вид функции root (с четырьмя, а не с двумя аргументами) неприменим, поскольку f (х) является положительноопределенной, и указать интервал, на границах которого она имела бы разный знак, невозможно.

Листинг 8.4. Поиск корня уравнения, заданного функцией двух переменных

Для того чтобы отыскать зависимость корней уравнения, вычисленных по одной переменной, от других переменных, разработаны специальные эффективные алгоритмы. Об одной из возможностей читайте в разд. 8.8.

Источник

Встроенные функции MathCAD для решения нелинейных алгебраических и трансцендентных уравнений

Уравнения в MathCAD решаются с помощью двух встроенных функцийroot и polyroots.

3.1.2.1 Встроенная функция MathCAD – root(F(x), x)

Для численного решения уравнений предназначена стандартная функция MathCAD – root(F(x), x), которая возвращает значение корня с заданной точностью. Функция root имеет два аргумента:

первый – выражение, стоящее в левой части уравнения, то есть F(x), второй – переменная, относительно которой решается уравнение, то есть x.

Ищется значение переменной x, при которой выражение F(x) обращается в ноль. Функция root возвращает значение переменной x, которая обращает выражение F(x) в ноль.

Функция реализует вычисление итерационным методом и перед её применением необходимо задать начальное значение переменной x, принадлежащее интервалу изоляции корня.

В зависимости от начального приближения функция root возвращает различные значения.

Решение уравнений с помощью функции root может производиться с различной точностью, которая задается значением системной переменной TOL.

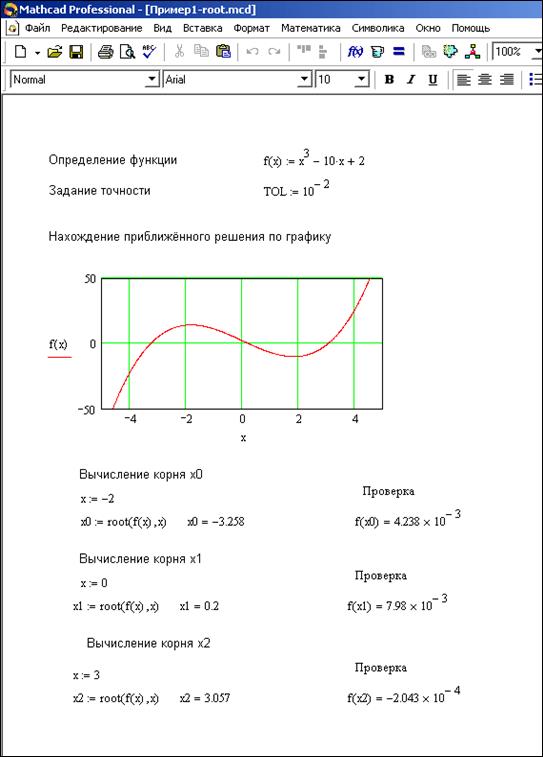
Пример 3.1 Решить уравнение с точностью .

Процесс решения показан на рисунке 1. Выполняется следующая последовательность действий:

1.Сначала вводится функция 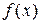, соответствующая левой части уравнения.

2. Задается точность.

3. Графически находится приближенное решение уравнения (можно использовать трассировку).

4. При помощи функции root выполняется нахождение решения уравнения с заданной точностью.

5. Выполняется проверка найденного решения.

В зависимости от начального приближения функция root возвращает различные значения. Результат решения задачи приведён на рисунке 3.1.1 В результате найдены корни x0=-3.258, x1=0.2, x2=3.057.

Рисунок 3.1.1 – Пример решения нелинейного алгебраического уравнения

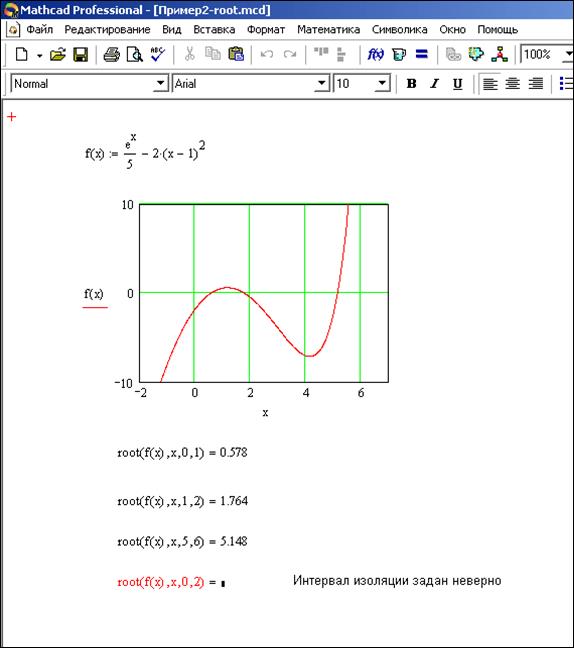
Результаты решения показаны на рисунке 2. Используя график функции, определяют пределы интервала изоляции каждого корня, а затем с помощью функции root (f(x), x, a, b) находят значение интересующего корня.

В данном случае найдено три корня. Необходимо правильно указывать интервал изоляции, в случае ошибки значение корня не будет найдено, что показано на рисунке 3.1.2

Рисунок 3.1.2 – Пример решения уравнения с использованием

функции root (f(x), x, a, b)

На рисунке 3.1.3 показан пример решения уравнения, имеющего комплексные корни. В таких случаях начальное приближённое значение корня также должно быть комплексным. При вводе мнимого числа надо писать 1i, а не i. В данном примере при вычислении второго корня х2 первый исключается делением f(х) на (х-х1). При нахождении третьего корня f(х) делится на (х-х1)(х-х2).

Рисунок 3.1.3 – Пример решения уравнения, имеющего

действительные и комплексные корни

Необходимо отметить особенность функции root, связанную с тем, что она не всегда позволяет найти значение корня.

Mathcad при поиске корня с помощью функции root использует метод итераций. Начальное значение, присвоенное переменной x, становится первым приближением к искомому корню. Когда значение выражения f(x) при очередном приближении становится меньше значения встроенной переменной TOL, корень считается найденным и функция root возвращает результат. Если после многих итераций Mathcad не может найти соответствующее приближение, то появляется сообщение об ошибке «отсутствует сходимость». Эта ошибка может быть вызвана следующими причинами:

— уравнение не имеет корней;

— корни уравнения располагаются далеко от начального приближения;

— выражение имеет локальные максимумы или минимумы между начальным приближением и корнем;

— выражение имеет разрывы между начальным приближением и корнями;

— выражение имеет комплексный корень, но начальное приближение было вещественным (или наоборот).

Чем точнее выбрано начальное приближение корня, тем быстрее функция root будет сходиться к точному решению.

Источник

Функция root в маткаде

Функция root() в Mathcad. Математика, информатика.

Для чего предназначена функция root() в Mathcad?

Простейший способ найти корень уравнения с одним неизвестным обеспечит функция root ( ). Аргументами функции root ( ) являются вид функции определяющей решаемое уравнение и имя переменой, относительно которой ищется решение – root (f(x),x) Если уравнение содержит несколько корней, то функция обеспечивает нахождение единственного корня, ближайшего к заданному начальному значению для искомой переменной. Точность вычислений может быть увеличена или уменьшена посредством задания значения переменной TOL, равной по умолчанию 10-3 и определённой в меню Math, Options (Математика, Опции). Установленное значение TOL также оказывает влияние на точность вычислений.

Уравнение с одним неизвестным: функция root

Для решения уравнения с одним неизвестным в Mathcad, помимо вычислительного блока Given/Find, предусмотрена встроенная функция root, которая, в зависимости от типа задачи, может включать либо два, либо четыре аргумента и, соответственно, использует разные алгоритмы поиска корней.

Первый тип функции root, аналогично встроенной функции Find, требует дополнительного задания начального значения переменной х, для чего нужно просто перед применением функции root присвоить х некоторое число. Таким образом, присвоение начального значения требует априорной информации о примерной локализации корня, т. к. поиск корня будет производиться вблизи этого числа. Пример работы функции root объясняется листингом 5.13.

Листинг 5.13. Два варианта уравнения методом секущих:

Как вы можете убедиться (первая строка листинга 5.13), для решения уравнения при помощи функции root (f (x),x,a,b) не требуется задавать начального приближения, а достаточно указать интервал [а,b]. Поиск корня будет осуществлен в промежутке между а и b альтернативным численным методом (Риддера или Брента). Когда root имеет четыре аргумента, следует помнить о двух ее особенностях. Во-первых, внутри интервала не должно находиться более одного корня, иначе будет найден один из них, заранее неизвестно, какой именно. Во-вторых, значения f (а) и f (b) должны иметь разный знак, иначе будет выдано сообщение об ошибке.

В чем же отличие встроенной функции Find от функции root? Оно состоит в том, что для решения одних и тех же задач используются различные численные алгоритмы (градиентные и метод секущих соответственно). В примерах уравнений с одним неизвестным, которые мы рассматривали до сего момента, выбор метода не влиял на окончательный результат, поскольку фигурировавшие в них функции были “хорошими”, т. е. достаточно гладкими для поиска корня одним из градиентных методов, требующих, как известно, вычисления производных. Между тем бывают ситуации, когда применение того или иного метода имеет решающее значение.

Приведем пример простой функции f(x), корни которой удается отыскать только при помощи функции root (листинг 5.14). Она определена в первой строке этого листинга, а ее корень вычислен во второй строке. Из графика, представленного на рис. 5.5, видно, что f (х) имеет особенность в окрестности своего корня, являясь в ней разрывной. В завершающей части листинга 5.14 предпринимается попытка отыскать нулевое значение f (х) посредством вычислительного блока Given/Find, которая оказывается неудачной.

Если Вы заметили ошибку, выделите, пожалуйста, необходимый текст и нажмите CTRL + Enter, чтобы сообщить об этом редактору.

Решение нелинейных уравнений

Вычисление корней численными методами включает два основных этапа:

· уточнение корней до заданной точности.

Рассмотрим эти два этапа подробно.

Отделение корней нелинейного уравнения

Пример. Дано алгебраическое уравнение

.

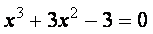
Определить интервалы локализации корней этого уравнения.

Пример. Дано алгебраическое уравнение

.

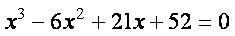
Определить интервалы локализации корней этого уравнения.

Уточнение корней нелинейного уравнения

Для уточнения корня используются специальные вычислительные методы такие, как метод деления отрезка пополам, метод хорд, метод касательных (метод Ньютона) и многие другие.

Функция root . В MathCAD для уточнения корней любого нелинейного уравнения (не обязательно только алгебраического) введена функция root , которая может иметь два или четыре аргумента, т.е. или , где – имя функции или арифметическое выражение, соответствующее решаемому нелинейному уравнению, – скалярная переменная, относительно которой решается уравнение, – границы интервала локализации корня.

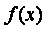
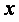
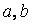
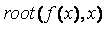
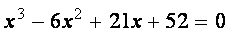
Пример. Используя функцию , найти все три корня уравнения , включая и два комплексных.

Заметим, что для вычисления всех трех корней использовался прием понижения порядка алгебраического уравнения, рассмотренный в п. 8.1.1. ¨

Функция root с двумя аргументами требует задания (до обращения к функции) переменной 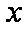начального значения корня из интервала локализации.

Пример 8.1.5. Используя функцию root , вычислить изменения корня нелинейного уравнения при изменении коэффициента а от 1 до 10 с шагом 1.

Ограничения содержат равенства или неравенства, которым должен удовлетворять искомый корень.

Функция Find уточняет корень уравнения, вызов этой функции имеет вид Find ( x ), где x – переменная, по которой уточняется корень. Если корня уравнения на заданном интервале не существует, то следует вызвать функцию Minerr ( x ), которая возвращает приближенное значение корня.

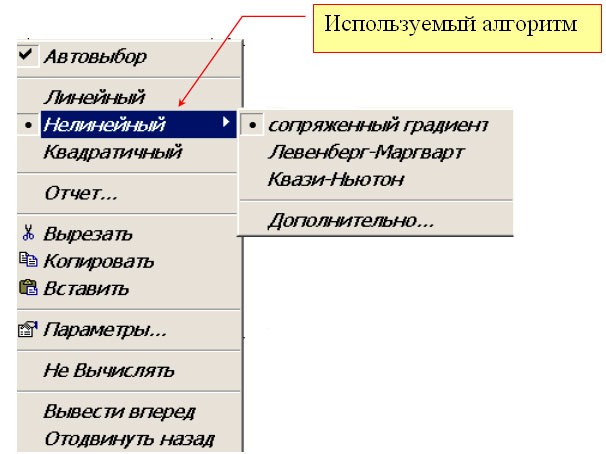
Для выбора алгоритма уточнения корня необходимо щелкнуть правой кнопкой мыши на имени функции Find ( x ) и в появившемся контекстном меню (см. рисунок) выбрать подходящий алгоритм.

Аналогично можно задать алгоритм решения и для функции Minerr ( x ).

Использование численных методов в функциях Find ( x ), Minerr ( x ) требует перед блоком Given задать начальные значения переменным, по которым осуществляется поиск корней уравнения.

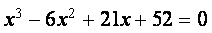
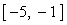
Пример. Используя блок Given , вычислите корень уравнения в интервале отделения .

7+1. Odesolve

Наша самая первая задача о движении моторной лодки туда и обратно (см. рис. 1 и 2) имеет существенное допущение: скорость лодки считается постоянной. Но это условие выполнить практически невозможно, т. к. лодка по прибытии в один конец пути должна сбросить скорость, развернуться и пуститься в обратный путь. Смоделировать снижение скорости лодки перед ее разворотом нам поможет функция Odesolve, предназначенная для решения (solve) обыкновенных (o – ordinary) дифференциальных (d) уравнений (e – equation) и их систем. Если при численном решении алгебраических уравнений и их систем мы получаем числа, подстановка которых в уравнения превращает их в тождества, то при решении дифференциальных уравнений и их систем мы получаем функции, подстановка которых превращает исходные дифференциальные уравнения в тождества. Заметим, что функция Odesolve в группе «Решение уравнений» стала восьмой (7 + 1 – см. выше) только в среде Mathcad Prime. В Mathcad 15 в группе «Решение уравнений» ее нет.

Итак, задача 4. На моторной лодке, движущейся со скоростью v, заглушили мотор. Спрашивается, как будут меняться скорость лодки и пройденный ею путь? Задача предельно упрощена – на лодку действует сила трения, пропорциональная квадрату скорости лодки (см. рис. 14, 15, 16 и 17, где этот квадрат фигурировал). На рисунке 18 показано решение и графическое отображение этой задачи с помощью функции Odesolve.

Рис. 18. Решение задачи об остановки лодки

Коэффициент пропорциональности, записанный в уравнении на рис. 18 (масса лодки, помноженная на ускорение – на первую производную скорости по времени), состоит из двух частей, связанных с трением о воздух надводной части лодки и трением о воду ее подводной части. Эти коэффициенты пропорциональны плотности ρ среды (воздуха или воды) и площади поперечного сечения надводной и подводной частей лодки S.

Задачу об остановке моторной лодки мы решили численно: функция Odesolve не ищет аналитического решения уравнения. Она формирует таблицу значений искомых функций v (скорость лодки) и x (пройденный путь), по которым интерполяцией создается непрерывная функция, по которой мы построили графики (см. рис. 18).

В среде Mathcad нет средств аналитического (символьного) решения дифференциальных уравнений. Но их можно поискать и найти в Интернете. На рисунке 19 показано такое решение – логарифмическая функция. Оно нашлось, поскольку исходное уравнение было достаточно простым. Но если с нашей задачи начать снимать ограничения, позволяющие упростить уравнение, то символьного решения уже не будет, и нам придется возвращаться к численным методам – к функции Odesolve. Так, например, при торможении лодки площадь поперечного сечения ее надводной части уменьшается, а подводной части растет[6]. Коэффициенты kвозд и kводы (см. блок исходных данных на рис. 18) также зависят от скорости и характера движения лодки: они одни при ламинарном («гладком») обтекании тела и другие при турбулентном движении, когда за лодкой клубятся вихри воды и воздуха. У воды и воздуха разная вязкость, что тоже нужно учитывать при математическом моделировании движении лодки. Этим занимается очень интересная наука под названием гидрогазодинамика…

Рис. 19. Символьное решение дифференциального уравнения

Каждая из рассмотренных функций «великолепной семерки Mathcad» обладает своими особенностями и ограничениями. Прежде чем приступать к решению задачи, следует продумать, какая из опций Mathcad приведет к поставленной цели, причем наилучшим образом.

Школьнику, студенту, инженеру или ученому необходимо (а в ряде случаев и достаточно) освоить «великолепную семерку Mathcad», особенности численных, графических и аналитических методов решения задач, чтобы успешно решать на компьютере свои учебные или профессиональные задачи.

Очков математики и математические пакеты // Открытое образование, №2, 2013. С. 23-34 (http://twt. mpei. ac. ru/ochkov/Mathcad-15/OchkovMath-pdf. pdf)

[1]Первое действие: как долго лодка была бы в пути, если б вода в реке была неподвижна – 2*10 км/12 км/ч = 1 час 40 минут; второе действие… Читатель, докончи это решение сам и сравни с теми, которые приведены ниже. Мы по действиям такие задачи решали когда-то в 5 классе школы. Но не всякая задача может быть решена по действиям. Поэтому и была придумана алгебра. Эту задачу тоже сходу нельзя решить пошагово. В древние времена, пока не было формулы корней квадратного уравнения, не всякое квадратное уравнение могли решить, причем решения были очень хитроумными.

[2] На этом и некоторых других рисунках будут показаны инструменты Mathcad Prime и Mathcad 15 для решения описываемых задач.

[3] А такими «нефизическими» формулами заполнены все учебники и задачники по математике. И это очень плохо. Хорошо тогда, когда за формулой скрывается какая-нибудь физическая реальность.

[4] Навстречу друг другу по одноколейной дороге одновременно вышли два поезда. И не столкнулись. Почему? Ответ: не судьба! 😉

[5] Мы имеем в виду знаменитое «Золотое сечение», т. е. такое деление отрезка на две неравные части, при котором длина отрезка так относится к длине большей части, как длина большей части относится к длине меньшей.

[6] Самые быстроходные суда те, у которых подводная часть минимальна: глиссирующие суда, суда на подводных крыльях или на воздушной подушке.

Решение систем уравнений

В зависимости от того, какие функции входят в систему уравнений, можно выделить два класса систем:

· алгебраические системы уравнений;

· трансцендентные системы уравнений.

Среди алгебраических систем уравнений особое место занимают системы линейных алгебраических уравнений (СЛАУ).

Системы линейных алгебраических уравнений

Системой линейных алгебраических уравнений (СЛАУ) называется система вида:

В матричном виде систему можно записать как

,

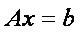
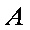
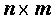
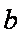
где – матрица размерности , – вектор с проекциями.

Для вычисления решения СЛАУ следует использовать функцию lsolve , обращение к которой имеет вид: lsolve (А, b ), где А – матрица системы, 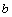– вектор правой части.

Решение систем нелинейных уравнений

MathCAD дает возможность находить решение системы уравнений численными методами, при этом максимальное число уравнений в MathCAD 2001 i доведено до 200.

Для решения системы уравнений необходимо выполнить следующие этапы.

Задание начального приближения для всех неизвестных, входящих в систему уравнений. При небольшом числе неизвестных этот этап можно выполнить графически, как показано в примере.

Пример. Дана система уравнений:

Определить начальные приближения для решений этой системы.

Видно, что система имеет два решения: для первого решения в качестве начального приближения может быть принята точка (-2, 2), а для второго решения – точка (5, 20). ¨

Следующие выражения недопустимы внутри блока решения:

· ограничения со знаком ¹ ;

· дискретная переменная или выражения, содержащие дискретную переменную в любой форме;

· блоки решения уравнений не могут быть вложены друг в друга, каждый блок может иметь только одно ключевое слово Given и имя функции Find (или Minerr ).

Пример. Используя блок Given , вычислить все решения системы предыдущего примера. Выполнить проверку найденных решений.

Пример. Используя функцию , вычислите решение системы уравнений

Источник